拉弯扭比例加载下50CrVA弹簧钢的多轴疲劳寿命及损伤特征

赵 凯，何玉怀，刘新灵，陶春虎

（北京航空材料研究院，北京100095）

多轴疲劳是指疲劳损伤发生在多轴加载条件下，即至少有两个或三个方向施加的应力独立地随时间发生变化。它们的变化可以是同相位、按比例的，也可以是非同相位、非比例的。相对于单轴疲劳而言，多轴疲劳无论在力学分析，实验研究，乃至物理机制方面都更为复杂。因为随着三个主应力（主应变）相对比值的改变，启动了更多的滑移系，裂纹可以在不同的方向和平面内形成。因此，在多轴疲劳情况下循环应力应变特性，裂纹的取向，形状，扩展方向，速率以及疲劳寿命等均将受到更多因素的影响。多轴疲劳的研究比单轴疲劳更加接近工程实际，且复杂载荷下疲劳行为的研究将进一步丰富人们对疲劳损伤机理和失效过程的认识，因此受到工程界和学术界的广泛关注［1－7］。近年来，人们逐渐认识到多轴疲劳问题的重要性，对其研究也逐渐深入［8－12］。航空航天、核电站、化工及车辆运输等领域的许多零部件都是在复杂的多轴应力状态下工作，并且多是因承受随机载荷作用而失效［13，14］。目前，大部分的科研仅集中于拉扭、拉拉、弯扭等双轴疲劳研究，而对拉弯扭等更为复杂的多轴疲劳方面的研究较少。

本工作通过设计偏心试样研究50CrVA弹簧钢在比例加载下的拉弯扭多轴疲劳性能，探索附加弯矩对试样疲劳寿命的影响，通过扫描电镜（SEM）对实验断口进行观察，研究多轴疲劳裂纹萌生及扩展机理。并对拉弯扭多轴疲劳进行了试探性研究，进一步丰富了多轴疲劳的研究成果，具有一定的工程指导意义。

1 实验材料和方法

50CrVA弹簧钢取自直径为35mm的棒材，其化学成分如表1所示。将棒材加工成毛坯后，对其进行热处理。热处理工艺过程：加热至860℃，保温1h后油淬→400℃／90min回火。试样材料经热处理后的力学性能：σb＝1480MPa，σ0.2＝1320MPa，δ＝12%，ψ＝47%。完成热处理工艺后再对毛坯进行精加工。

表1 50CrVA弹簧钢的化学成分（质量分数／%）Table1 Chemical composition of 50CrVA spring steel（mass fraction／%）

采用MTS 809拉－扭电液伺服材料试验机，所有实验均在室温空气介质下进行。为使试样产生附加弯矩，在实验过程中，通过重新设计偏心试样来模拟弯扭复合疲劳实验。标准试样形状和尺寸如图1（a）所示。在此基础上将试样改进成偏心试样，所谓偏心试样即工作部分的轴线平行偏离试样整体轴线一定距离。当施加轴向载荷时偏心试样会受到附加弯矩。因此，当对偏心试样进行拉扭复合疲劳实验时，偏心试样还受到附加弯矩的作用，实际上是对偏心试样进行拉弯扭复合疲劳实验。在本实验中，偏心试样的偏心量为0.50，0.75，1.00mm。偏心试样（偏心量1.00mm）的形状和尺寸如图1（b）所示。各试样均为光滑试样，精加工完成后用砂纸打磨试样表面以消除表面残余应力。

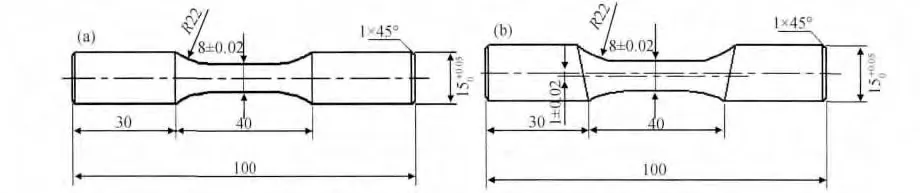
图1 标准试样（a）和偏心试样（1.00mm）（b）的形状和尺寸Fig.1 The shape and size of the standard specimen（a）and eccentric specimen（1.00mm）（b）

施加的载荷：轴向拉力波形为正弦波，幅值为9kN。扭矩波形也为正弦波，幅值为90N·m。实验应力比R＝0.1，频率为10Hz。两个波形同步，无相位角即比例加载。

2 结果分析与讨论

2.1 偏心试样受力分析

偏心试样共受三类载荷作用：轴向拉力、附加弯矩和扭矩。

轴向拉应力幅值σp计算公式［15］

式中：Fmax是作用在偏心试样上的轴向拉力幅值；d是偏心试样的直径。计算可知，各试样的轴向拉应力均为180MPa。

对偏心试样施加轴向拉力时，由于偏心量的存在会产生附加弯矩，在附加弯矩的作用下产生的弯曲应力幅值σd计算公式［15］

式中e是偏心量。计算可知，标准试样和不同偏心量（0.50，0.75，1.00mm）下偏心试样的轴向应力幅值分别为0，90，135，180MPa。

对于偏心试样所承受的载荷，利用叠加原理［15－17］，将弯曲应力与轴向应力进行叠加。偏心试样轴向应力幅值的计算公式

计算可知，标准试样和不同偏心量下轴向应力幅值分别为180，270，315，360MPa。

扭转切应力幅值τmax的计算公式［15］

式中Tmax为扭矩幅值。计算可得各试样的扭转切应力幅值均为900MPa。

可知，各试样扭转切应力和轴向拉应力均相同，所不同的是偏心试样在轴向拉力的作用下会产生附加弯矩，偏心量越大，所产生的弯曲应力也越大。

2.2 附加弯矩对疲劳寿命的影响

图2为各试样弯曲应力－疲劳寿命关系图。可以看出，试样的疲劳寿命并没有随着弯曲应力幅值的增大而出现显著降低。各试样的弯曲应力幅值为0～180MPa。由 Von Mises等效应力［18］σeq＝计算可得各试样的等效应力为1570～1600MPa。则各试样的弯曲应力幅值不超过等效应力的11%，扭转切应力为等效应力的57%左右。因此，各试样的弯曲应力占等效应力比重较小，对试样的疲劳寿命影响不大；扭转切应力占等效应力比重较大，对试样的疲劳寿命有较大影响。各试样的扭转切应力均相同，因此其疲劳寿命相差较小。

图2 各试样的弯曲应力－疲劳寿命关系Fig.2 The relationship of bending stress－fatigue life for specimens

2.3 复合加载损伤特征

2.3.1 断口宏观特征

图3为试样疲劳断口侧面形貌。用Olympus SZ61体视镜对各试样的断面法线与试样轴线之间的夹角进行测量，标准试样的夹角相对较大，约为40°（图3（a））；对于各偏心试样而言，夹角为5～20°不等，各偏心试样之间并没有明显差别（图3（b）～（d））。所有试样的断面均呈现螺旋走向。对于纯扭转疲劳断口，断面通常与轴线约呈45°。对于拉弯扭疲劳断口，在轴向拉应力的作用下，裂纹不再单纯沿与轴线约45°截面扩展，裂纹也沿垂直轴线方向扩展。因此，断面法线与试样轴线之间的夹角要小于45°，且理论而言，轴向应力越大，夹角越小。对于各偏心试样而言，轴向拉应力均相同，所不同的是弯曲应力。如前所述，各偏心试样弯曲应力的值相比于等效应力均小很多。因此随着偏心量的增大，各偏心试样断面夹角并不会出现很明显的差别。

标准试样以及偏心试样（1.00mm）的断口形貌如图4所示。两试样的断口均呈灰色，部分区域磨损较严重，这主要是裂纹面的两侧有规律的反复张合以及扭转加载下裂纹面两侧的研磨所致。两断口均未见明显塑性变形和疲劳弧线。可观察到源区，疲劳扩展区和瞬断区。源区为点源特征，疲劳裂纹萌生于试样表面，因为试样表面的扭转切应力最大。标准试样的断口较为粗糙，有明显的剪切唇，剪切唇因擦伤而呈现光亮；偏心试样（1.00mm）的断口相对平坦，剪切唇面积较小，断口擦伤更严重，因为偏心试样还要承受附加弯矩的作用。如前所述，弯曲应力与轴向拉应力相叠加，使得裂纹面两侧的反复张合幅度更大，偏心试样的断口磨损更严重。标准试样的疲劳扩展区所占面积约为断口的1／5；偏心试样（1.00mm）的疲劳扩展区所占面积约为断口的1／10。可以发现，试样的疲劳扩展区随着轴向应力的增大而减小，瞬断区随着轴向应力的增大而增加。可见轴向应力的增大会在一定程度上加速疲劳裂纹的扩展。

图4 标准试样（a）以及偏心试样（1.00mm）（b）的断口形貌Fig.4 Fracture surface morphology of standard specimen（a）and eccentric specimen（1.00mm）（b）

2.3.2 断口微观特征

扫描电镜（SEM）下观察偏心试样（1.00mm）的断口，源区高倍形貌如图5（a）所示（图4（b）中①位置）。源区附近未见冶金缺陷，可观察到明显的放射棱线。在整个断口上不易观察到疲劳条带。在疲劳扩展前期可见轮胎花样（图5（b），图4（b）中②位置）。对于单轴拉压加载下的低周疲劳断口，轮胎花样和脊骨花样为其主要微观特征。轮胎花样是一种擦伤的疲劳裂纹痕迹，疲劳裂纹形成后，裂纹面的两侧有规律的反复张合，相对于面上的棱角或硬的夹杂物使断口擦伤［19］。在疲劳扩展后期沿周向分布有较多的二次裂纹，在此附近可观察到少量疲劳条带。疲劳裂纹的扩展方向有两个：周向和径向（图5（c），图4（b）中③位置），周向分布的疲劳条带与二次裂纹平行。对于单轴拉压疲劳试样，其疲劳条带一般沿与轴线垂直的径向分布。在纯扭转加载下，所萌生的疲劳裂纹位于平行和垂直于试样轴线的两个方向上，这两个方向均承受循环剪切应力作用［20］。拉弯扭复合作用下，断口上的疲劳特征为综合应力作用的结果，沿径向分布的疲劳条带主要是轴向应力作用的结果，沿周向分布的疲劳条带则主要是扭转切应力作用的结果。瞬断区主要以剪切拉长韧窝特征为主，其是扭转疲劳断口的典型特征。瞬断区有明显的擦伤痕迹（图5（d），（e），图4（b）中④位置）。

图5 断口的微观形貌（a）源区放大图；（b）轮胎花样；（c）疲劳条带；（d）擦伤痕迹；（e）韧窝＋擦伤Fig.5 Microscopic morphologies of fracture surface（a）magnification image of source region；（b）tire patterns；（c）fatigue striations；（d）trace of scratch；（e）dimples and scratch

从微观观察来看，试样在复合作用力的作用下沿周向与径向扩展。由于扭转切应力较大而轴向应力较小，因此可推断周向为疲劳裂纹扩展的主方向，而径向为次方向。两个方向相互垂直，互不影响。周向分布的疲劳裂纹在扭转切应力的作用下扩展速率快，首先扩展到临界尺寸后发生失稳扩展，而此时径向的疲劳裂纹尚未扩展到临界尺寸。扩展速率较快的疲劳裂纹决定了试样的疲劳寿命即扭转切应力决定了试样的疲劳寿命。各试样的轴向应力虽不同，但扭转切应力均相同。因此，各试样疲劳寿命相差不大。可以推断，当轴向应力继续增大至与扭转切应力所占等效应力比重相近时，轴向应力会对试样的疲劳寿命产生明显影响。

3 结论

（1）对于拉弯扭复合疲劳加载，当附加弯矩产生的弯曲应力幅值不超过等效应力的11%时，附加弯矩的存在对试样的疲劳寿命影响较小。

（2）拉弯扭复合疲劳加载的断面存在严重的擦伤痕迹；疲劳源区，疲劳扩展区和瞬断区均较为明显。断口源区为点源特征，疲劳裂纹萌生于试样表面。疲劳扩展区的面积随着轴向应力幅值的变化而不同，轴向应力幅值越大的试样，其疲劳扩展区面积越小。

（3）拉弯扭复合疲劳加载的断口上，疲劳条带不易观察到。在疲劳扩展前期可以观察到轮胎花样。疲劳裂纹的扩展方向有周向和径向两种。断口上的疲劳特征为综合应力作用的结果，沿径向和周向分布的疲劳条带分别为轴向应力作用和扭转切应力作用的结果。

［1］张午.非比例加载下疲劳累积损伤规律的研究［D］.南京：南京航空航天大学，2007.

［2］刘德刚，王凤洲，林春虎.国外疲劳研究及应用领域的新发展［J］.铁道车辆，2001，39（9）：10－12.LIU De－gang，WANG Feng－zhou，LIN Chun－hu.Foreign fagitue research and new development of application fields［J］.Railway Vehicle，2001，39（9）：10－12.

［3］陈旭，许爽燕.多轴低周疲劳研究现状［J］.压力容器，1997，14（3）：58－61.CHEN Xu，XU Shuang－yan.Recent developments of multiaxial low cycle fatigue failure prediction［J］.Pressure Vessel，1997，14（3）：58－61.

［4］尚德广，姚卫星.基于临界面法的多轴疲劳损伤参量的研究［J］.航空学报，1999，20（4）：295－298.SHANG De－guang，YAO Wei－xing.Study on multiaxial fatigue damage parameters based on the critical plane approach［J］.Acta Aeronautica Sinica，1999，20（4）：295－298.

［5］GLINKA G，PLUMTREE A，SHEN G.A multiaxial fatigue strain energy parameter related to the critical plane［J］.Fatigue Fract Eng Mater Struc，1995，18（1）：37－46.

［6］ELLYIN F，GOLOS K.Multiaxial fatigue damage criterion［J］.J Eng Mater Technol，ASME，1988，110（1）：63－68.

［7］LOHR R D，ELLISON E G.A simple theory for low cycle multiaxial fatigue［J］.Fatigue Fract Eng Mater Struc，1980，3（1）：1－17.

［8］BANNANTINE J A，SOCIE D F.A variable amplitude multiaxial fatigue life prediction method［A］.KUSSMAUL K，MCDIARMIDD，SOCIE D，et al.Fatigue Under Biaxial and Multiaxial Loading ESISl0［C］.London：Mechanical Engineering Publications，1991.35－5l.

［9］WANG C H，BROWN M W.A path－independent parameter for fatigue under proportional and non－proportional loading［J］.Fatigue Fract Eng Mater Struc，1993，16（12）：1285－1298.

［10］WANG C H，BROWN M W.Life prediction techniques for variable amplitude multiaxial fatigue—part 1：theories［J］.Journal of Engineering Materials and Technology，1996，118（3）：367－370.

［11］WANG C H，BROWN M W.Life prediction techniques for variable amplitude multiaxial fatigue—part 2：comparison with experimental results［J］.Journal of Engineering Materials and Technology，1996，118（3）：371－374.

［12］KIM K S，PARK J C，LEE J W.Multiaxial fatigue under variable amplitude loads［J］.Journal of Engineering Materials and Technology，1999，121（3）：286－293.

［13］庄茁，蒋持平.工程断裂与损伤［M］.北京：机械工业出版社，2004.97.

［14］赵云，蒙秋红，王国安.滑移装载机轮边轴断裂原因分析［J］.失效分析与预防，2011，6（3）：174－177.ZHAO Yun，MENG Qiu－hong，WANG Guo－an.Fracture analysis of wheel－side axle of skid loader［J］.Failure Analysis and Prevention，2011，6（3）：174－177.

［15］刘鸿文.材料力学［M］.3版.北京：高等教育出版社.1992.

［16］李同林.应用弹塑性力学［M］.武汉：中国地质大学出版社，2002.

［17］徐秉业，刘信声.弹塑性力学及其应用［M］.北京：清华大学出版社，1995.

［18］尚德广，王德俊.多轴疲劳强度［M］.北京：科学出版社，2007.

［19］上海交通大学.金属断口分析［M］.北京：国防工业出版社，1979.

［20］尚德广.多轴疲劳损伤与寿命预测研究［D］.沈阳：东北大学，1996.