基于支持向量机的Laplacian网格曲面孔洞修补算法

许 斌，李忠科，宋大虎

（第二炮兵工程大学 计算机教研室，陕西 西安710025）

0 引 言

使用扫描仪获取模型表面的三维数据时，由于物体表面反射性、扫描设备的缺陷、模型表面的自遮挡等原因，点云数据通常含有孔洞，进而导致重构后的网格曲面也存在着孔洞。孔洞的存在极大地影响了模型的完整性和显示效果，在工业应用场合则会导致后续操作无法进行，因此，对这些孔洞进行修复是曲面网格模型数据处理的一个关键步骤。

从实际应用角度考虑，一个好的曲面修复算法应尽可能地满足下面两个条件：①修复曲面尽量接近原始真实形状，与周围网格有很好的光顺连接；②算法有较强的鲁棒性，即能够处理各种类型孔洞。总体来说，孔洞的修复问题可以归结为空间多边形的三角剖分问题，很多学者都对这个问题进行了深入研究，下面对其中一些具有代表性的算法进行简要介绍。文献 ［1］提出了一种采用体数据场融合进行孔洞修补的算法，该算法首先迭代计算扩展体数据场的描述范围，然后在此基础上建立一个能够描述整个孔洞区域及其周围曲面的场函数来完成孔洞缺失数据的修复。文献 ［2］使用RBF隐式曲面来对孔洞曲面进行修复，算法中首先计算孔洞边界顶点的邻域顶点，然后根据其几何属性插值生成孔洞区域的RBF隐式曲面，最后对该曲面进行网格化处理并与原始网格曲面进行融合得到孔洞修复后的网格曲面。上述几种算法的优点是能够修复较大的孔洞，但是对于缺失部分包含丰富几何细的模型来说上述几种修复方法就存在局限性，因为它们不能很好地恢复模型缺失部分的几何细节。

文献 ［3］提出了一种基于PDE （partial differential equations）方法的孔洞修复方法，该方法首先分析模型的几何特征，然后采用正交梯度的方法来修复孔洞模型。Remacle等［4］提出了一种在孔洞边界采样点和缺失部分曲面定点之间建立调和映射的孔洞修补算法，最后通过最小化一个带约束的全局能量函数来实现对缺失部分集合特征的修复。Park等［5］提出一种基于局部参数化的孔洞模型几何和纹理的修复算法，该算法首先通过孔洞检测算法检测出孔洞，然后对待修复区域进行局部参数化，再通过自选择或者人机交互在模型上选择一块相似的区域来填补孔洞，最后通过解Poisson方程将选择区域变形移植到孔洞区域，从而完成孔洞模型几何和纹理的修复。

近年来，神经网络及支持向量机等智能化的机器学习方法被大量应用到网格曲面的孔洞修补中，用以推断缺失部分曲面的几何特征。文献 ［6］使用混合径向基函数模拟网格曲面缺失部分顶点坐标与原始网格曲面顶点坐标之间的函数关系，该算法能够较好地恢复修补曲面的几何特征；文献 ［7］在此基础上将遗传算法、模拟退火法和BP网络方法相结合，在一定程度上提高了算法的效率，但是生成网格的质量不高；文献 ［8］中的方法也存在类似问题。

综合上述各种算法可以看出，由于孔洞部分的几何信息已经完全缺失，怎样根据模型已有部分的几何特点推断出缺失部分的几何信息，是网格曲面孔洞修复的根本难点所在。以神经网络和支持向量机等机器学习系统为基础的修补算法正是针对这一核心难点提出的。本文采用在统计学习理论的基础上发展起来的新一代机器学习方法［9］支持向量机 （support vector machines，SVM）作为几何信息回归手段，结合当前非常流行的网格曲面Laplacian坐标，提出了一种全新的，针对三角网格曲面模型的孔洞修复算法，该算法突出的优点就是能最大限度地使修补后的曲面在几何风格上与模型曲面原有部分保持一致。

1 主要数学工具

本文中使用的两种核心数学工具是网格曲面的Laplacian坐标和最小二乘支持向量机，其作用分别是描述网格曲面的几何细节，和依据孔洞周围部分曲面的几何信息对孔洞缺失部分曲面的几何信息进行回归推断。

1.1 网格曲面上的Laplacian坐标

网格上的Laplacian坐标是一种描述网格模型几何细节的数学工具，顶点Vi处的Laplacian坐标的计算公式如式（1），Vj是顶点Vi的局部片中的任意一点

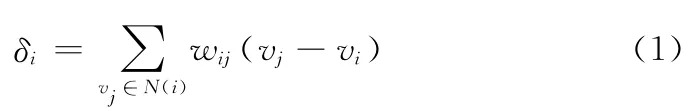
Laplacian坐标根据权重的不同分别是同一Laplacian坐标和余切Laplacian坐标，本文采用余切Laplacian坐标

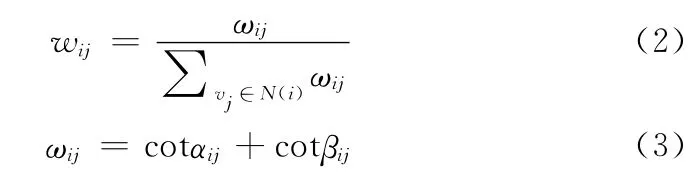
式 （2）、式 （3）是权重系数计算公式，采用式 （2）和式 （3）计算出来的就是顶点Vi处的余切Laplacian坐标，记做δi。如式 （4）所示余切Laplacian在数值上线性逼近网格顶点处的平局曲率，方向上逼近该点的主曲率法向，可以非常准确地描述网格顶点的局部片的几何特性

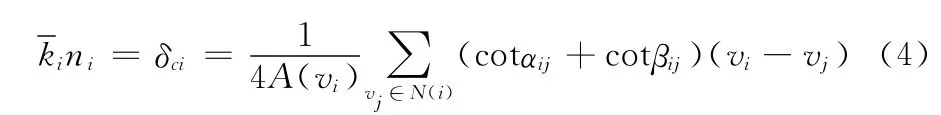
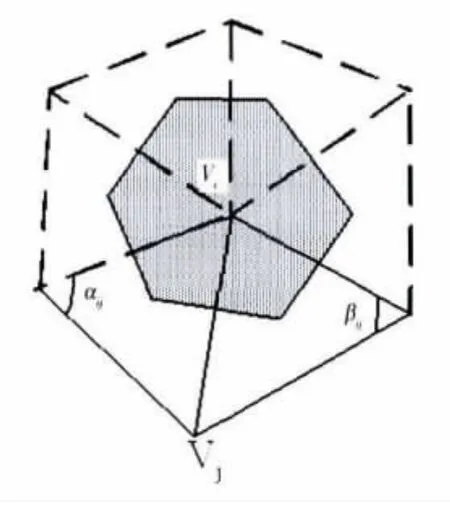
图1 顶点Vi的局部片

在计算网格顶点的Laplacian坐标时，本文使用n×n阶的Laplacian矩阵L，n为需要计算的网格区域内的顶点数

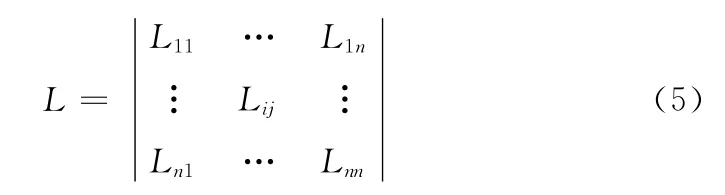
式 （5）中的Lij的形式如式 （6）所示

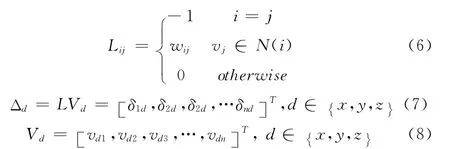
式 （8）中的Vd是顶点坐标在某一坐标轴方向的分量，式 （7）中的Δd是Laplacian坐标在某一坐标方向的分量。

1.2 最小二乘支持向量机

最小二乘支持向量机 （least－squares support vector machines）是由Suykens提出的，这种方法采用最小二乘线性系统作为损失函数，突出优点是求解速度快，鲁棒性强。最小二乘支持向量机在本文中的应用是一个典型的回归问题，回归的目标是最优化函数f（x）。本文给定训练样本集（如式 （9）所示）为孔洞周围区域网格顶点的某一空间坐标和Laplacian坐标在同一坐标轴方向的分量

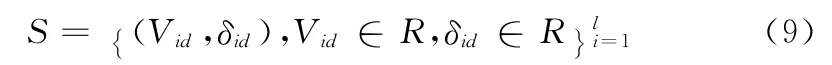
式中：d∈ ｛x ，y ，z｝，l——训练样本集中的样本数量。平衡考虑回归函数的复杂度和拟合误差，依照结构风险最小化原理，将本文中的回归问题描述为下面的约束优化问题

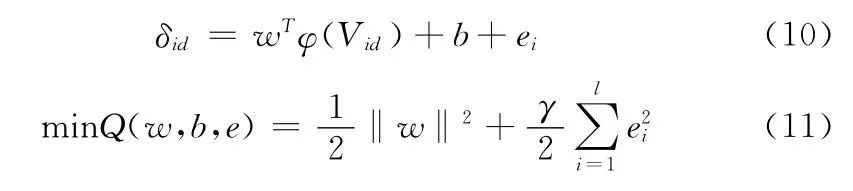
式 （11）中的w是权矢量，ei是松弛变量，γ为正则化参数，b为偏差量，为求解上述优化问题，需要建立Lagrange函数 （如式 （12）所示）

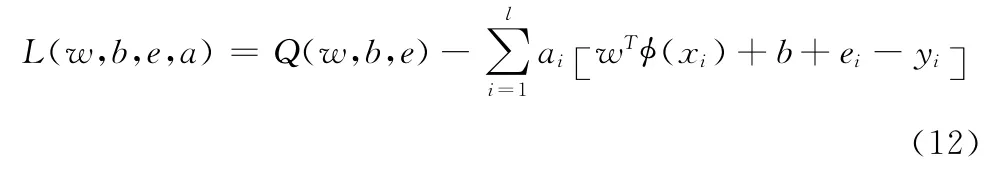
式中：a＝ （a1，a2，…，al）为 Lagrange乘子，在 KKT 最优化条件 （Karush－kuhn－Tuchker）下优化函数各变量的偏导数，并在鞍点处得到零值［10］（如式 （13）所示）

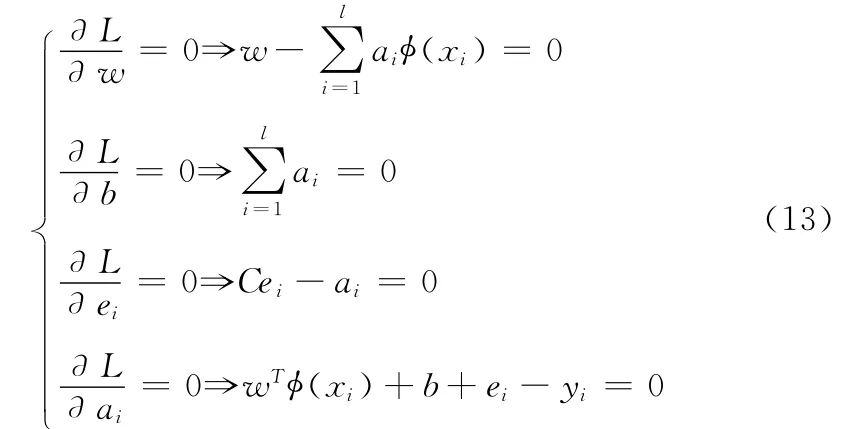
将式 （13）写成矩形形式，并消去w和e可以得到式（14）

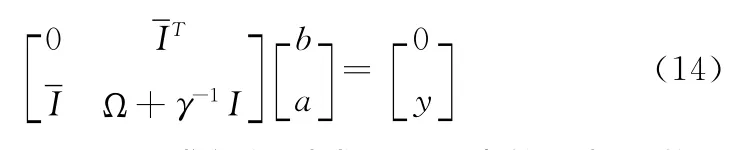
式中：Ωij＝K（xi，xj），求解得到式 （15）中的回归函数

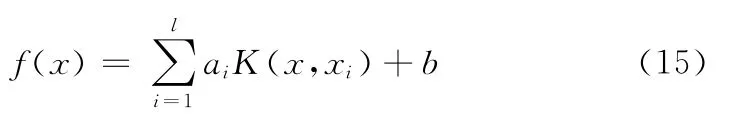
2 算法具体流程

本文算法分为以下4个部分：①孔洞边界处理：包括孔洞边界检测与边界边预处理；②孔洞平面网格填充：包括建立孔洞特征平面、孔洞平面缺失采样点估计与孔洞平面的网格生成；③三维缺失数据获取：包括训练样本集的采集和最小二乘支持向量机回归函数求解；④空间网格生成：包括三维空间中孔洞区域修补网格的生成。

2.1 孔洞边缘检测

在三角网格曲面上孔洞通常是由那些只包含于一个三角形的边组成的，这些边都属于模型的边界边。为了能够加快边界检测速度，本文采用层次空间剖分技术来对点云数据进行剖分。目前层次空间剖分技术主要包括八叉树、四叉树、BSP树和K－D树等，其中八叉树表现出了优良的特性。因此，采用八叉树来加快边界检测的速度。边界检测算法的具体步骤如下：

步骤1 计算每个三角网格的中心以及它和三角形顶点间的联系；

步骤2 通过三角网格的中心建立八叉树；

步骤3 搜索八叉树，检测与它相关的边的拓扑连接性，如果某条边只属于一个三角形，则是边界边。

步骤4 通过顶点的不同几何连通性分辨出不同的边界回路，表示出不同的孔洞。

2.2 孔洞边界预处理

由于在实际测量中孔洞区域的数据信息非常少，因此，重构后孔洞边界处的三角片形状可能会不理想，会出现一些狭长的三角片。这些三角片上的边同其它边界边不协调，在孔洞填充时会造成不好的影响。为了降低这种影响，本文先对孔洞边界进行预处理，将一些比较长的边进行剖分，然后再对孔洞进行修补。

设vi（i＝1，2，…，n）为孔洞边界上的n个顶点，ε为孔洞边界上的边，则孔洞边界预处理可以分为三步。

步骤1 计算孔洞边界上所有边的平均长度Lave。

步骤2 遍历所有的边，如果存在某一条边εij＝ （vi，vj）的长度Lεij＞k·Lave，k为比例系数 （本文中取k＝2），则计算边εij的中点vnew。

步骤3 将vnew增加为孔洞的边界点，同时删除原来的边界边εij与三角片vvivj，增加边界边vivnew、vivnew和三角片vivvnew、vnewvvj，如图2所示。最后迭代执行上一步操作，直到边界边没有变化为止。

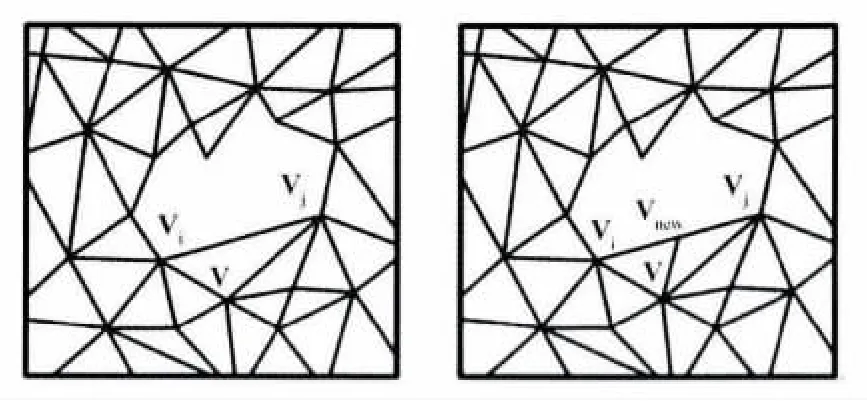
图2 孔洞边界预处理

2.3 建立孔洞特征平面

孔洞特征多边形的平面化是通过将特征多边形投影到特征平面上实现的，所以特征平面的选取是一个关键步骤，设Ve＝ ｛vi，i＝1，2，…，m｝为孔洞的边界点集合，本文选取与Ve中的所有点的距离平方和最小的平面作为特征平面，这样的特征平面的法向量如式 （16）所示

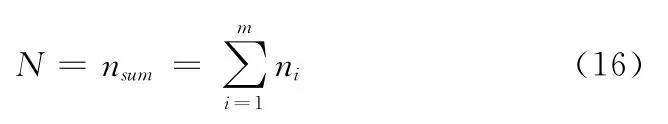
式中：N——特征平面法向量，nsum——孔洞周边所有三角面片法矢量的向量和，这样的法平面选取可以保证N和最后修复得到的孔洞部分填充曲面的主法向量 （所有新生三角面片的矢量和）偏差最小，进而保证对平面三角化后得到的修补网格顶点进行重新定位时Laplacian坐标的旋转失真最小。

2.4 特征面平面上的孔洞填充

为了提高最终生成的三角网格质量，本文提出一种基于步长均值采样的孔洞平面缺失数据估计算法来估计孔洞平面内缺失的数据，其基本思想是使用两组步长相等的平行线对孔洞平面均值采样，孔洞平面内的交点即为估计的数据。算法的具体步骤如下：

步骤1 在特征平面内求取孔洞特征多边形的最小包围盒；

步骤2 计算投影后边界边的平均边长珚Lb；

步骤3 以珚Lb为步长，用两组互成60°的平行线对特征多边形的包围盒均匀采样，如图3所示。

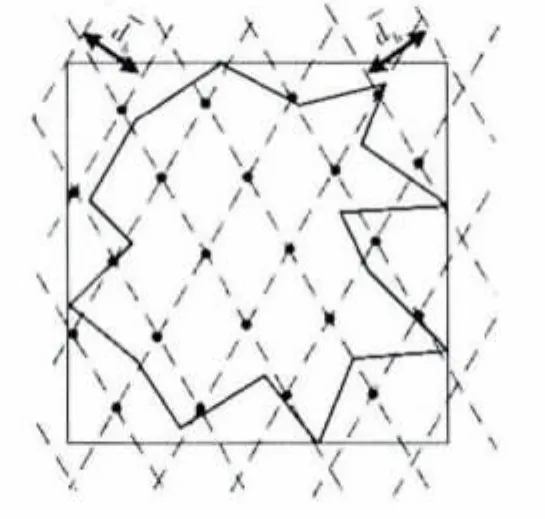
图3 孔洞特征多边形均值采样

步骤4 采用多边形内外点判断方法对步骤3中的交点进行判断，保留特征多边形的内点；

步骤5 分别计算步骤4中所得估计点与边界边和边界点间的距离le和lp，如果le＜0.2珚Lb或是lp＜0.2珚Lb，则删除对应的估计点。

步骤6 最终所剩下的点则为所要计算的缺失数据点，如图4（a）所示。

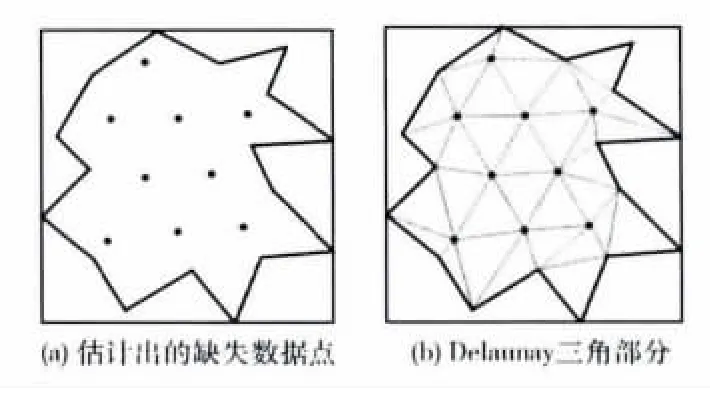
图4 孔洞平面网格填充

在特征平面内通过采样得到缺失数据点的坐标值之后，需要生成三角网格以方便后续的处理。直接在局部坐标系下将上一步求得的数据点与孔洞的边界点一起进行Delaunay三角剖分，得到三角网格，完成孔洞平面的网格填充，填充后的网格如图4（b）所示。

2.5 为最小二乘支持向量机选取学习样本

迄今为止所有的孔洞修复算法都是依据已有网格曲面的几何特征去推测缺失部分曲面的几何特征，本文算法就是选取孔洞周围的点及改点上Laplacian坐标作为最小二乘支持向量机的训练样本集，在实现过程中以孔洞边界为中心不断向外扩展，逐层采集相邻几层的三角形顶点，直到采集到满足需要的层数为止。

假设Ve为孔洞边界B 上的顶点集合，SVj（j＝0，1，…k）为孔洞外面第j层的顶点集合，样本采集的具体算法如下：

步骤1 在边界上取出一点vi，然后寻找与它相关的三角面片顶点，如果该顶点不在Ve中，则将它加入到孔洞的下一层顶点集SV1中；

步骤2 遍历数组Ve中的每一个顶点，重复步骤1，这样就采集到了由孔洞多边形向外的第一层三角片顶点，并存放在顶点集SV1中；

步骤3 对顶点集SVj（j＝1，2…k－1）中的顶点，寻找与它相关的三角形的顶点，并将不在SVj和SVj－1中的点加入到顶点集SVj＋1中；

步骤4 迭代执行步骤3，直至采集达到所设定的层数为止，则SVj（j＝0，1，…k）中所有的点及其Laplacian坐标即构成了训练样本集，采样点分布如图5所示。

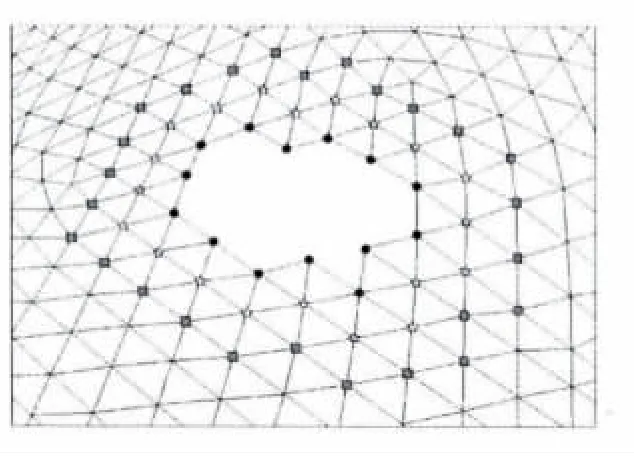
图5 为最小二乘为支持向量机选取的样本点集

2.6 填充部分顶点的重新定位

将第2.5小节中得到的训练样本集代入最小二乘支持向量机，按照2.2小节中的方法可以得到3个回归函数：fx（x），fy（x），fz（x）。

设定Vnew为2.4小节中填充的新顶点集合。式 （17）中的V′nd是对Vnew中的顶点重新定位后的顶点坐标在某一坐标轴方向上的分量，重新定位的过程是对网格顶点坐标的3个分量分别进行求解，求解的是式 （18）中所示的n×n的线性系统，n为Vnew中顶点数

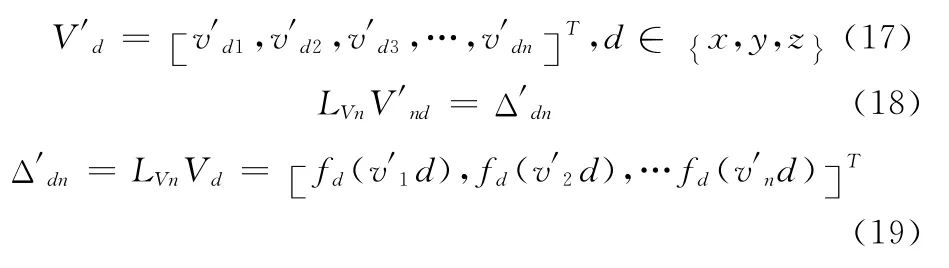
式 （18）中的LVn是在2.4小节中剖分得到的修补三角网格上，按照2.1小节中的方法建立的余切Laplacian矩阵，Δ′dn是重新定位后的修补区域网格顶点余切Laplacian坐标的某一分量构成的向量，是按照式 （19）构造的。式（19）中的fd（v′nd）是由回归函数推测出的缺失区域网格顶点的Laplacian坐标的某一分量。

3 算法评价及实验结果

为了检验本文算法的实际性能，以Visual C＋＋2010为开发平台，结合OpenGL图形库实现了文中算法，并在head模型和happyvrip模型上进行了对比试验，试验结果如下：

图6 中的模型就是head模型，在头发部分人为制造了一个孔洞，作为待修补孔洞。试验中选取的对比算法为传统的直接修复算法和文献 ［11］中的算法，之所以选择文献 ［11］算法是因为该算法和本文算法都是基于最小二乘支持向量机的，区别主要是文献 ［11］算法直接将网格顶点的一个欧氏坐标分量做回归函数的输出，而本文引入了网格顶点的余切Laplacian坐标作为回归函数的输出，再以由回归函数推断得到的缺失部分网格曲面的Laplacian坐标为基础建立线性系统求解得到缺失部分的网格顶点坐标。

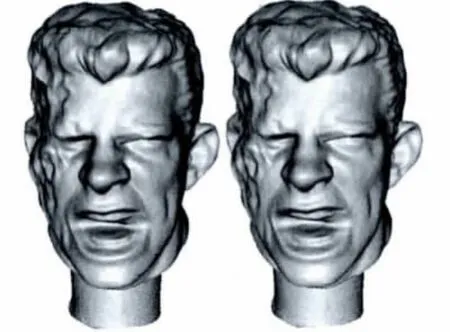
图6 原始head模型和制造孔洞后的head模型

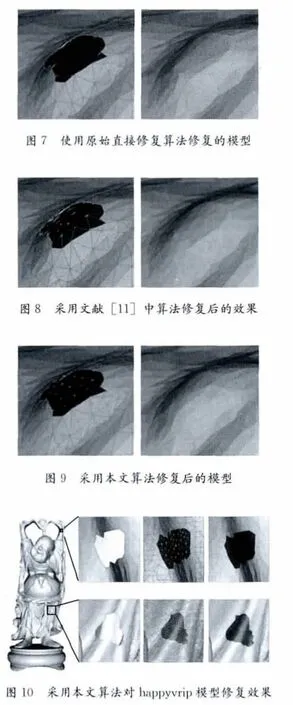
图7 中是使用原始的直接修复算法得到的修付效果，明显比较粗糙。图8中是使用文献 ［11］中算法得到的修复效果，效果很好，修复区域的网格曲面质量也不错。图9是使用本文算法得到的修复效果，修复区域的网格质量也很好，同时可以看到相对于文献 ［11］中的算法，使用本文算法的到的修补曲面与原始曲面的融合度明显更高，效果与没有制造孔洞前的原始模型曲面几乎没有差别。

图10 是使用本文算法对happyvrip模型的修复效果，这个试验的目的是检验本文算法在高曲率曲面上的修复效果，在具体实验中，为了应付高曲率环境，加大了2.5小节中支持向量机的训练样本的选取范围 （head试验中的选取范围是孔洞外的3层点，happyvrip试验中为7层点），从试验结果看本文算法对高曲率曲面的修复效果也是比较理想的。

4 结束语

本文算法的创新点在于引入了网格顶点的余切Laplacian坐标作为回归函数的输出，并通过求解线性系统的方式对修复区域的网格顶点进行二次定位，这样做的优势是发挥了Laplacian坐标对网格曲面几何细节的刻画能力，可以使修复后的网格曲面与原始曲面融合的更加自然。

本文算法的局限性在于对面积过大的孔洞的修复效果不理想，这也是目前所有的曲面修复算法面对的共同问题，对付这个问题的根本途径是在构建修复区域网格时不仅要以孔洞周围曲面的几何特性作为依据，还要考虑模型的整体几何特征，这也是本文下一步研究和改进的方向。

［1］Geuzaine C，Remacle J.Gmsh：A three－dimensional finite element mesh generator with built－in pre－and post－processing facilities ［J］.International Journal for Numerical Methods in Engineering，2009，79 （11）：1309－1331.

［2］Wu X，Wang M，Han B.An automatic hole－？lling algorithm for polygonal meshes ［J］.Computer－Aided Design and Applications，2008，5 （6）：889－899.

［3］Marchandise E，Piret C.CAD and mesh repair with radial basis functions［J］.Journal of Computational Physics，2012，231 （5）：2376－2387.

［4］Remacle J，Geuzaine C，Compère G，et al.High quality surface remeshing using harmonic maps ［J］.International Journal for Numerical Methods in Engineering，2010，83 （4）：403－425.

［5］Marchandise E，Carton de Wiart C，Vos W，et al.High quality surface remeshing using harmonic maps—Part II：Surfaces with high genus and of large aspect ratio ［J］.International Journal for Numerical Methods in Engineering，2011，86（11）：1303－1321.

［6］Wright G B，Flyer N，Yuen D.A hybrid radial basis function－pseudo－spectral method for thermal convection in a 3dspherical shell［J］.Chemistry Geophysics Geosystems，2010，11 （7）：1－18.

［7］CHEM Jie，GAO Chenghui，HE Bingwei.Automatic recognition of boundary features of non－closed triangulation model［J］.Machinery Design ＆ Manufacture，2011 （11）：89－94.

［8］Macdonald C B，Ruuth S J.The implicit closest point method for the numerical solution of partial differential equations on surfaces［J］.SIAM Journal on Scienti？c Computing，2009，31（6）：4330－4350.

［10］WU Dehui.Intelligent prediction model for surface roughness in milling ［J］.Computer Integrated Manufacturing Systems，2007，13 （6）：1137－1141 （in Chinese）.

［11］LIU Deping，YU Shuijing.Hole repairing in triangular meshes based on least－squares support vector machines ［J］.Computer Integrated Manufacturing Systems，2009，15 （9）：1868－187（in Chinese）.［刘德平，于水晶.基于最小二乘支持向量机的三角网格修补算法 ［J］.计算机集成制造系统，2009，15 （9）：1868－187.］