基于粗糙集理论的冗余规则处理方法

陈 超，陈性元，汪永伟，代向东

（1.信息工程大学，河南 郑州450004；2.河南省信息安全重点实验室，河南 郑州450004）

0 引 言

当前，网络安全设备在一定程度上保护了网络系统的安全，但是依然存在一些问题。第一，各类安全设备由于误报、语义弱等问题产生了海量的不确定安全数据，这些海量的信息难以通过人工的方式进行管理与分析；第二，各类安全设备收集了与网络安全相关的数据，其中存在大量冗余信息，增大了数据处理难度；第三，各类安全设备大都局限于对网络存在的漏洞进行探测与分析，缺乏对安全数据的深层挖掘，难以形成对网络安全状况的整体认识。因此，迫切需要对包含不确定和冗余信息的海量数据进行有效处理。

目前，针对上述问题的处理方法主要有概率论[1]、可信性理论[2]、证据理论[3]和粗糙集理论[4]等。其中，粗糙集理论借助其能够客观处理海量数据和利用属性约简剔除冗余数据等优势成为当前的研究热点。但是，粗糙集理论在处理海量数据时形成的知识库很庞大且知识库中含有较多的冗余和错误知识。如何剔除知识库中存在的冗余和错误知识、自动提取出用户感兴趣的、新颖的知识是基于粗糙集的数据处理中迫切需要解决且实际存在的一个问题。

规则是粗糙集中知识的表现形式，借助规则评价[5]可以有效剔除冗余规则。目前，规则评价方法中使用比较广泛的是统计学和信息理论领域的规则兴趣度量和规则质量度量[6－8]，但是这两种方法的通用性不好；规则－属性约简[9]借鉴粗糙集中属性约简的概念，把规则作为新决策表中的条件属性进行约简找出约简属性集，从而剔除大量规则，但是，这种方法仅仅以原始数据集为出发点，不包含任何领域知识，可能剔除用户感兴趣的规则。文献[10]提出了综合主观领域知识和客观度量的规则重要性评价方法，对规则进行重要性排序，但是没有剔除冗余规则，且会产生与事实不符的规则。文献[11]提出了将客观评价标准和主观评价标准结合在一起的思想，产生一个包含主客观的度量标准，但是存在评价指标权重难以确定的问题；文献[12]将所有的主客观度量方法融合在一起进行计算，能够有效的进行规则评价，但是主观综合评价和客观综合评价的权重存在比较大的随意性。

综上所述，当前客观规则评价方法可以剔除大量冗余规则，同时也会剔除大量有用规则；主客观相结合的规则评价方法中评价指标的权重难以确定，而且这些方法没有建立一个好的架构将评价结果与实际情况进行对比。

1 系统结构

本文设计的冗余规则处理系统如图1所示，整个系统由数据预处理模块、规则获取模块、规则评价模块和权重度量模块组成。

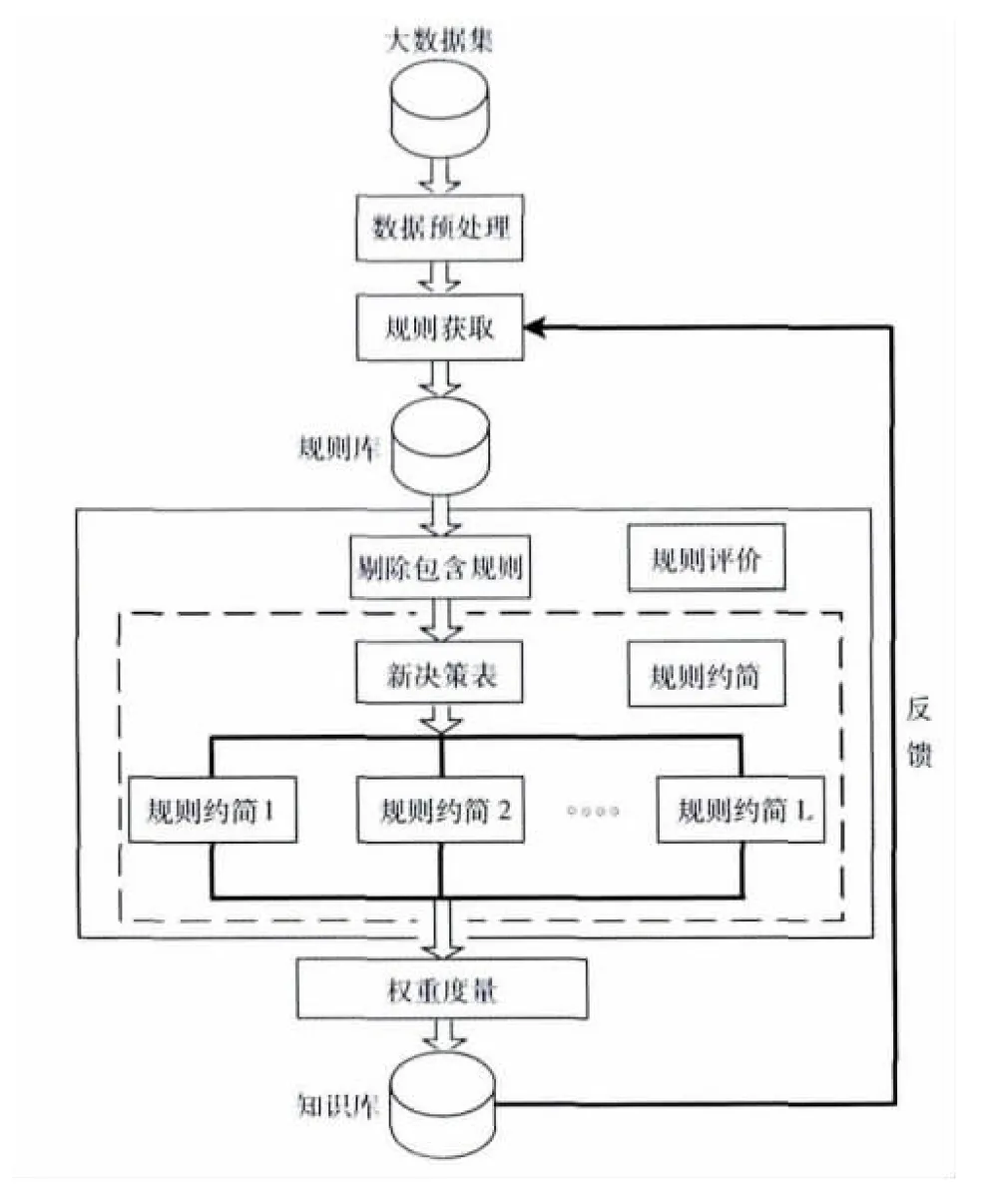
图1 基于粗糙集的冗余规则处理过程

本文的数据集来源于各安全设备所产生的历史数据，包括入侵日志、流量信息、漏洞信息等。

数据预处理模块主要是将数据集组织成粗糙集中决策表的形式，并对决策表进行数据离散化和属性约简。离散化是数据预处理模块的核心。由于粗糙集理论只能处理离散数据，因此为了便于分析，在尽可能少地丢失有用信息的基础上，利用离散化方法将决策表中的连续数据转化为离散数据。对于不同的数据类型，根据简单实用的原则采用不同的方法。

规则获取模块使用规则生成算法对预处理之后的决策表进行规则产生，从而形成规则库。

规则评价模块通过定义包含规则的形式并将其从规则库中剔除，在此基础上利用规则约简剔除冗余规则。

权重度量模块通过规则重要性标准对剩余的规则进行重要性排序，形成知识库，并引入专家对知识库中的规则进行评判，当没有达到预定效果时，通过反馈来调整规则获取模块中的各项参数，使得知识库中的规则都是用户感兴趣的规则。下面给出规则评价模块和权重度量模块的详细设计。

2 基于规则评价的冗余规则剔除

针对冗余规则的剔除，当前已提出了很多方法，例如，利用规则的支持度、信度等为标准剔除由噪音产生的冗余规则，利用属性重要性的概念剔除包含属性重要性为零的规则等。针对网络安全领域的应用背景，本文选择粗糙集理论剔除冗余规则，这是因为，第一，粗糙集理论不需要先验概率，而各安全设备产生的数据具有一定的不确定性，导致规则的先验知识难以获取；第二，粗糙集理论中的属性约简能够正确剔除数据集中的冗余数据，为冗余规则的剔除提供了新思路。

2.1 粗糙集理论

粗糙集理论是波兰数学家Z.Pwalak于1982年提出的一种用来刻画不确定性和不完整性的数学工具[13]，它建立在分类机制的基础上，将知识理解为对特定空间的划分。下面简要介绍粗糙集理论中几个比较重要的概念。

定义1 决策表是一个四元组IS＝（U，A，V，f），其中，U 是论域 （对象构成的集合，U＝｛x1，x2，x3，。。。，xm｝）。A是属性的非空有限集合，A＝C∪D且C∩D＝，C为条件属性集，D为决策属性集，一般D只含有一个属性。V是属性值的集合。信息函数f指定U中每一个对象x的属性值。

定义2 等价关系是用来表达由于缺乏一定的知识而不能区别已知决策表中的某些对象。设决策表IS＝（U，A，V，f），则BA所对应的等价关系数学表达式如下

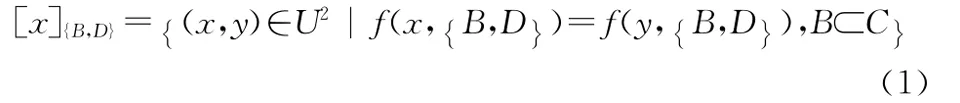
定义3 属性重要性是指条件属性对决策属性的重要程度，任意一个条件属性ai的属性重要性表达式如下

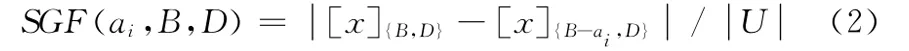
式中:——对象个数。

定义4 属性约简就是在保持数据库分类能力不变的前提下，删除其中不相关或不重要的数据。

属性约简就是删除属性重要性为零的条件属性，约简结果包含能够代表整个数据集的重要属性，且决策表中可能存在多个约简。属性约简是决策表的本质部分。

定义5 属性核是决策表的属性全集中所有必要属性构成的集合，记为core（A），它是所有约简的交集。

定义6 决策规则是知识的表现形式，其表示方法为A－＞B，其中A为规则前件，表示条件属性集C中属性描述符的合取，B为规则后件，是对决策属性d的描述。

2.2 包含规则

由于规则获取模块会产生大量的规则，而这些规则中有些规则会被其它规则所包含，这些规则不仅不能够带来有用信息，而且会增大规则规模，增加规则的存储空间。因此，在规则评价过程中必须剔除包含规则。

假设规则集中存在多个规则，其形式分别为:

R1:＜条件属性1，条件属性2＞－＞＜决策属性值＞

R2:＜条件属性1，条件属性2，条件属性3＞－＞

＜决策属性值＞

R3:＜条件属性1，条件属性2，条件属性5＞－＞

＜决策属性值＞

则称规则R1包含规则R2和R3，R2和R3是R1的包含规则。

从包含规则的形式可以看出，被包含规则R2和R3不仅具有规则R1相同的两个条件属性和决策属性值，还具有其它的条件属性。

2.3 规则约简

大数据集中存在冗余数据的现象，所以约简就是非常必要的。粗糙集理论中的属性约简通过删除属性重要性为零的数据以剔除冗余数据。一个约简是原始数据集中条件属性的子集，它具有和条件属性全集相同的分类能力，因此，约简含有数据集中最具代表性的数据。基于上述分析，把数据集中产生的单个规则作为条件属性建立新的决策表，对新的决策表进行属性约简可以剔除冗余属性，从而提取重要属性，其对应的规则也是重要规则，即约简规则。因此，一个约简中的规则是非常重要的，而不是约简中的规则就是冗余规则。由于属性约简是基于约简算法自动产生的，所以通过这种方法可以自动剔除冗余规则。

2.3.1 新决策表的建立

由规则约简的思想可知，它建立在以规则为条件属性的决策表的基础上。为了保证新决策表与原始决策表保持一致，同时对新决策表进行属性约简所产生的规则与原有规则保持一致，在建立新决策表的过程中必须遵循以下原则:

（1）新决策表的对象个数和决策属性值必须和原始决策表一致。

（2）新决策表的表中元素值必须是原有规则和原始决策表对象间的一种映射关系。

设原 始 决 策 表IS＝（U，A，V，f），U＝｛x1，x2，x3，…，xm｝是对象集，c＝｛c1，c2，…，cn｝ 是条件属性集，D是决策属性集且只包含一个属性。对原始决策表进行规则获取产生的规则集为R＝｛R1，R2，…，Rk｝ 。建立新的决策表的过程如下。

设新的决策表为pm＊（k＋1），其中m代表决策表中拥有的对象个数，｛R1，R2，…，Rk｝ 是决策表中的列，即条件属性集，D＝d作为决策表的决策属性。如果一个规则的条件属性值和决策属性值与原始决策表中某一个对象的条件属性值和决策属性值相同，我们称之为这个规则与原始决策表中的这个对象相匹配。如果规则Ri与原始决策表中的对象xj相匹配，则赋予新决策表中第j行第i列的值p[j，i]为1，否则为0。新决策表中的决策属性值和原始决策表中的决策属性值保持一致。确定新决策表中各个条件属性值的公式如下所示

2.3.2 约简规则和核规则

定义7 对新决策表进行属性约简得到约简属性，其对应本文的约简规则。

由于属性约简是通过剔除冗余数据来提取重要数据，因此约简规则中不包含冗余规则。

定义8 新决策表中所有约简规则的交集为核规则。

由于核规则存在于每一个约简规则中，而约简规则是最具代表性的规则，因此核规则是所有规则中最重要的规则。

3 基于权重度量的规则重要性排序

利用规则评价模块对规则库进行冗余规则的剔除之后，其规模依然很庞大，人们无法从这些规则中找出对决策起关键作用的规则。因此，剩下的规则中每一个规则是否同等重要，如果不是，那么规则的重要程度如何评价。只有解决了上述两个问题，才能够真正的帮助人们做出正确的决策。

权重度量:由粗糙集理论的基本概念可知，对决策表进行属性约简可能存在多个结果，而每一个约简结果都能够完全描述决策表，即属性约简中的条件属性集能够对决策属性进行正确分类。假设使用某种约简算法寻找约简属性集时，如果只产生一个属性约简，那么这种约简算法会造成信息的丢失，因为可能存在其它的条件属性集能够对决策属性进行正确分类。如果某种约简算法能够产生更多的属性约简，那么这种算法所产生的多个属性约简将带来更多的信息。由于寻找决策表的所有属性约简是N－P问题[10]，所以只能寻找某种约简算法产生尽量多的属性约简，使得更多的属性约简带来更加丰富的信息。

约简属性是非常重要且最具代表性的属性，核属性是所有约简的交集，它存在于所有的属性约简中，是最重要的属性。借鉴上述概念，我们认为如果规则约简中的非核规则在所有约简中出现的频度越高，那么其重要程度也越高。因此，规则的重要程度可以通过规则的出现频率来度量，其判断公式如下所示

式中:L——规则约简个数，αL（Ci）——规则Ci在L个属性约简中的出现次数。

4 示 例

设原始数据集为一决策表，其数据见表1。

表1 原始数据集

假设基于表1产生了6个规则R1、R2、R3、R4、R5和R6，其表达式如下:

规则R1:如果不发生网络蠕虫攻击，则当前网络状态为安全。

规则R2:如果发生木马攻击，且带宽利用率正常，则当前网络状态为安全。

规则R3:如果发生木马攻击，且带宽利用率不正常，则当前网络状态为不安全。

规则R4:如果不发生木马攻击，且带宽利用率正常，则当前网络状态为安全。

规则R5:如果发生网络蠕虫攻击，则当前网络状态为不安全。

规则R6:如果不发生木马攻击，且带宽利用率不正常，则当前网络状态为不安全。

在这个例子中，m＝4表示在原始决策中共有4个数据对象，k＝6表示在规则集中共有6个规则。用来确定重要规则的新决策表可表示为p[4，7]，新决策表中的条件属性为规则R1、R2、R3、R4、R5和R6，决策属性保持不变，依然为d。在新的决策表中，由于规则R1与原始数据集中的第一行不匹配，所以p[1，1]＝0，由于规则R2与原始数据集中的第二行相匹配，所以p[2，2]＝1。同理可得到决策表中其它元素的值，其结果见表2。

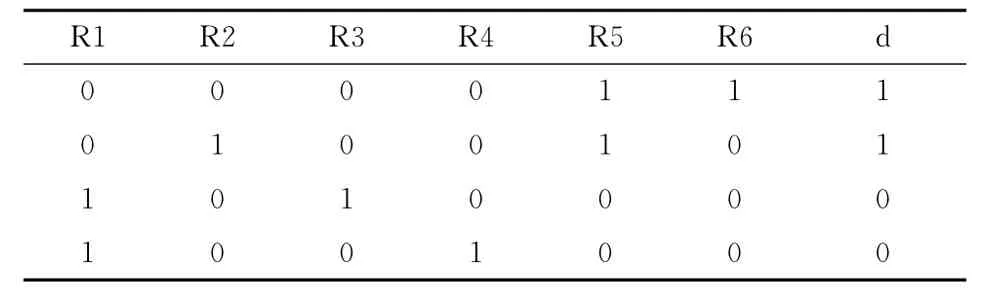
表2 新决策表

假设基于表2产生了两个属性约简，分别为｛R2，R6｝和｛R3，R4｝，非约简中的规则R1和R5是冗余规则，依照式 （4）对约简中的4个规则进行重要性排序。μR2＝1／4＝25%，μR3＝1／4＝25%，μR4＝1／4＝25%，μR6＝1／4＝25%，得到的规则重要性排序见表3。

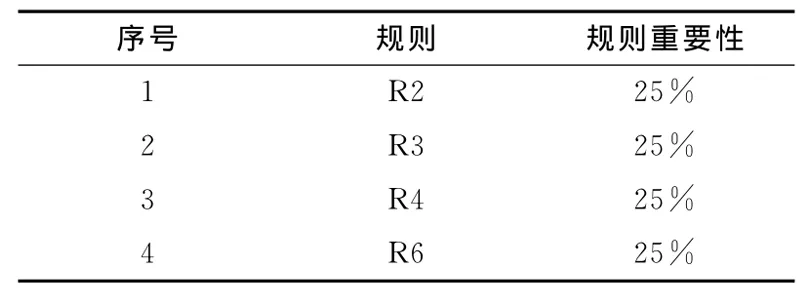
表3 规则重要性排序

5 实验验证

为验证本文所提方法的有效性，本文以版本号为V1.4.41、基于Rough集理论框架的表格逻辑数据分析工具包ROSETTA为开发工具对上述方法加以实现，并与文献[9，10]的实验结果进行对比。

5.1 数据源处理

为了能够与实际情况进行对比，本次实验选取的是关于汽车的数据集[14]，它是用来确定汽车的英里数，数据集中共包含14个数据对象和8个条件属性，其中条件属性（make＿model，cyl，door，displace，compress，power，trans，weight）分别用 （A，B，C，D，E，F，G，H）表示，决策属性英里数Mileage用d表示，数据集中Med表示Medium。

在汽车数据集中不存在不一致数据和不完整数据，利用ROSETTA中的遗传算法[15]产生两个约简，其结果见表4。在两个约简的基础上共产生14条规则。

表4 得到的多个属性约简

5.2 规则处理

通过ROSETTA得到原始数据集的两个约简和14条规则，利用规则约简建立新的决策表，在新的决策表基础上使用ROSETTA的遗传算法得到20个属性约简，通过权重度量对规则进行重要性排序。采用本文方法及文献[8，9]所示方法得到的结果见表5、表6和表7。表5的规则中前五项为条件属性，mileage为决策属性，空白处表示规则中没有此条件属性，例如序号5表示的规则为:make＿model（USA）＾compress （High）＾trans （Auto）＝＞mileage（Medium）。

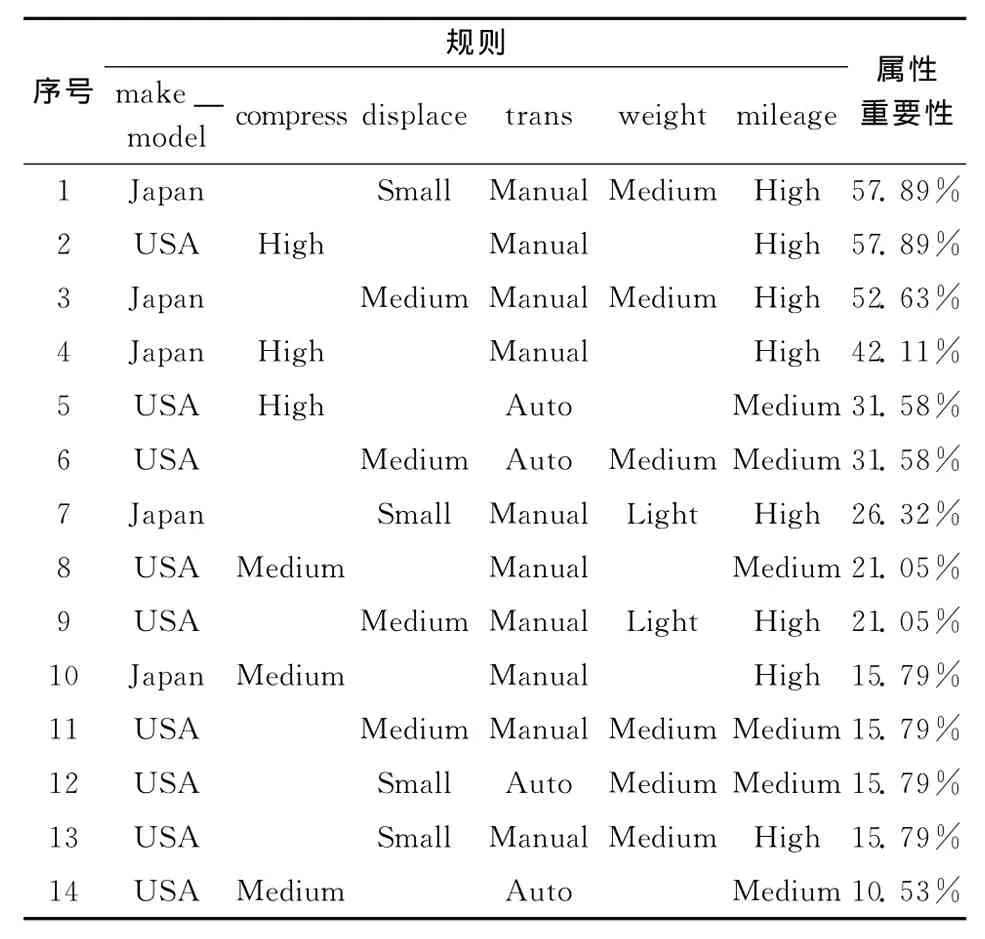
表5 规则评价方法的实验结果

表6 属性约简的实验结果

表7 重要性度量的实验结果

5.3 对比分析

文献[9]指出，如果在原始数据集中没有进行属性约简或引入规则模板将会产生6327条规则，从表5、表6和表7可以看出3种方法都非常有效的减少了规则规模且在大部分规则都包含重要属性。基于属性约简的规则评价方法在规则规模削减方面效率最高，但是只产生两个规则，丢弃了大量含有重要属性的规则，且没有对规则进行重要性排序；基于规则重要性度量的规则评价方法产生了13个规则，且对规则进行了重要性排序，但是存在多个不包含重要属性的规则，如规则 “Door（4）＝＞mileage（Medium）”，这个规则与我们对汽车的经验认识不相符，汽车拥有2个门或4个门对汽车行驶的英里数影响不大，因此，这个方法产生了与事实不符的规则，会误导决策者。和表5进行对比可知，表5中的14个规则都包含重要属性，且在规则重要性排序中，两个规则的重要性程度最高，如规则R1的重要性为57.89%，其内容为make＿model（Japan）＾displace（Small）＾trans（Manual）＾weight（Medium）＝＞mileage（High），这与我们对汽车的经验相符。自动档的汽车比手动档的汽车更加省油，日本车以消耗更少的汽油和运行更长的英里数而著称，通过本文所示方法可以保证人们根据规则非常迅速的做出正确的决策。

6 结束语

为了剔除基于粗糙集理论的数据处理中的冗余规则，并对剩余的重要规则进行排序，提出了冗余规则处理架构。该架构中的规则约简用一种新的视角看待属性约简的概念，把原始数据集中产生的规则作为新决策表中的条件属性。因此，新决策表中的约简结果剔除了冗余规则，并利用粗糙集理论中核属性的概念作为剩余规则的权重度量标准。实验结果表明，本文提出的方法能够有效的剔除冗余规则。在实际环境中，大数据集产生的规则规模一般都非常庞大，因此本文方法具有很大的实际应用价值。为了提高本文方法的有效性，必须产生足够多的属性约简，这也是该方法以后的改进方向。

[1]Toshiyuki Nakajima.Probability in biology:Over view of a comprehensive theory of probability in living systems[J].Progress in Biophysics and Molecular Biology，2013，113 （1）:67－79.

[2]SUN Hongxiang.A preliminary study of credibility theory and its security library[D].Beijing:Beijing University of Posts and Telecommunications，2008 （in Chinese）.[孙洪祥.可信性理论及其在安全库方面的初步研究[D].北京:北京邮电大学硕士学位论文，2008.]

[3]JIANG Liming，HE Jialang，ZHANG Hong.A new conflict evidence fusion method in D－S evidence theory[J].Computer Science，2011，38 （4）:236－238 （in Chinese）.[蒋黎明，何加浪，张宏.D－S证据理论中一种新的冲突证据融合方法[J].计算机科学，2011，38 （4）:236－238.]

[4]Yao Y，Yao B.Covering based rough set approximations[J].Information Sciences，2012，200:91－107.

[5]CHEN Peng，TAN Li，YU Chongchong.Evaluation and application of domain－oriented association rules[J].Computer Engineering and Design，2011，32 （7）:2385－2390 （in Chinese）.[陈鹏，谭励，于重重.面向领域的关联规则评价及其应用[J].计算机工程与设计，2011，32 （7）:2385－2390.]

[6]Nicholls G D O，Powers C R，Gardner K C，et al.Method and apparatus for distributed rule evaluation in a near real－time business intelligence system:U.S.Patent 8，001，185[P].2011－08－16.

[7]Fürnkranz J，Gamberger D，Lavra cˇN.Rule evaluation measures[M].Foundations of Rule Learning.Springer Berlin Heidelberg，2012:135－169.

[8]Zeichner N，Berant J，Dagan I.Crowdsourcing inference－rule evaluation[C]／／Proceedings of the 50th Annual Meeting of the Association for Computational Linguistics:Short Papers－Volume 2.Association for Computational Linguistics，2012:156－160.

[9]Jiye Li，Nick Cercone.A method of discovering important rules using rules as attributes[J].International Journal of Intelligent Systems－Granular Computing:Models and Applications，2010，25 （2）:180－206.

[10]Jiye Li，Nick Cercone.Introducing a rule importance measure[G].Lecture Notes in Computer Science 4100:Transactions on Rough Sets V，2006:167－189.

[11]Marketsmueller S.Methods and apparatus for fill rule evaluation over a tessellation:U.S.Patent 8，237，710[P].2012－08－07.

[12]Abe H，Tsumoto S，Ohsaki M，et al.Improving a rule evaluation support method based on objective indices[J].International Journal of Advanced Intelligence Paradigms，2010，2（2）:180－197.

[13]WANG Guoyin，YAO Yiyu，YU Hong.Rough set theory and research on the application[J].Journal of computer，2009，32 （7）:1229－1246 （in Chinese）.[王国胤，姚一豫，于洪.粗糙集理论与应用研究综述[J].计算机学报，2009，32 （7）:1229－1246.]

[14]Hu Xiaohua.Knowledge discovery in databae:An attribute－oriented rough set approach[D].University of RegIna，1995.

[15]Witold Pedrycz，Mingli Song.A genetic reduction of feature space in the design of fuzzy models[J].Applied Soft Computing，2012，12 （9）:2801－2816.