基于3D-DCT和混沌加密的医学体数据多水印算法
刘瑶利,李京兵
(海南大学 信息科学技术学院,海南 海口570228)
0 引 言
数字水印技术作为信息隐藏技术研究领域的重要分支,是实现多媒体信息完整性保护的有效方法[1],它是对传统的加密技术的有效补充。将病患的个人信息作为数字水印[2],以人眼看不见的形式嵌入到医学体数据中,在体数据经历了信息交流过程中的数据处理后[3,4],将水印完整准确得提取出来,从而达到保护病患个人信息的目的。
目前,将水印嵌入二维图像的方法很多。叶天语等人[5]利用奇异值的稳定性,提出一种多功能双水印算法;董春华等[6]提出了基于小波变换在医学图像中嵌入多水印的方法;刘泉等[7]基于图像的认证提出了分层半脆弱数字水印算法;陈海鹏等[8]基于数字图像特征提出一种鲁棒性数字水印算法。然而,在实际应用中,三维医学体数据在数字医疗系统中大量存在,如CT、MRI都是由切片组成的三维体数据。因此,将水印嵌入三维体数据有更好的实用性。医学体数据对于医生获取患者的生理疾病信息及病情诊断至关重要,一般不允许作任何改动[9]。
1 基础理论
1.1 Logistic混沌映射
混沌是非线性动力系统中的一种确定性的类随机过程,混沌信号对初始值有不可预测性和高度敏感性[10]。Logistic Map是一种著名的混沌系统,它是由以下公式给出的非线性返回映射
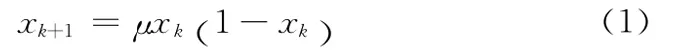
式中,0≤μ≤4称为增长参数,xk∈(0,1)为系统变量,k是迭代次数。混沌动力系统的研究工作指出,当增长参数3.569945≤μ≤4时,Logistic Map工作于混沌状态。应用Logistic混沌映射产生的混沌序列是一个理想的密钥序列,可用于对多水印进行混沌加密。
1.2 三维离散余弦变换 (3D-DCT)
三维离散余弦正变换公式如下
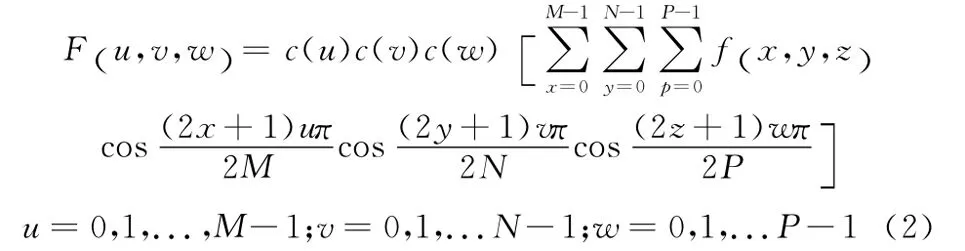
其中
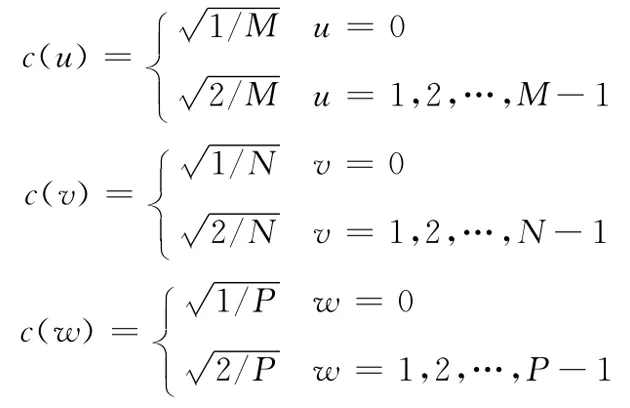
式中:f(x,y,z)是体数据V在 (x,y,z)处的体素数据值,F(u,v,w)是该体素数据对应的三维DCT变换系数。
三维离散余弦反变换 (3D-IDCT)公式如下

式中 :(x,y,z)—— 空 间 域 采 样 值 ;(u,v,w)—— 频率域采样值。医学体数据可通过CT和MRI获得,体数据是由许多层的切片组成,每个切片为二维医学图像,大小为M×N,切片层数为P。
2 算法过程
嵌入医学体数据的多重水印为:Wk={wk(i,j)|wk(i,j)=0,1;1≤i≤M1,1≤j≤M2,k≥1};同时,选取Matlab中自带的一个MRI体数据作为原始医学体数据,表示为:F={f(i,j,k)|f(i,j,k)∈R;1≤i≤M,1≤j≤N,1≤k≤P}。wk(i,j)表示多水印的像素灰度值,f(i,j,k)表示原始医学体数据的体素数据值。
2.1 体数据视觉特征向量的选取方法
将数字水印直接嵌入在体素或变换系数中不能有效的抵抗几何攻击,因为体数据的轻微几何变换就会导致体素数据值或变换系数值发生较大变化,这样嵌在体数据中的数字水印便会轻易的受到攻击。不同体数据的三维轮廓在视觉上是有很大差异的,而且在经历微小的几何变换之后其三维轮廓能够基本保持一致。通过对大量体数据的三维DCT系数观察发现,当对一个体数据进行常见的几何变换后 (通过对每个切片进行几何变换来实现),三维DCT低中频系数值的大小可能发生改变,但其系数符号基本保持不变。因此,三维DCT系数符号可以作为医学体数据的主要视觉特征。
对原始医学体数据进行全局三维DCT变换,得到三维DCT系数矩阵。选取8个DCT低中频系数FD(1,1,1)-FD(2,2,2)组成医学体数据的特征向量。三维DCT系数正值或零用 “1”表示,负值用 “0”表示。通过观察表1发现,体数据在受到常规攻击和几何攻击后,三维DCT低中频系数符号序列基本保持一致,与原始三维体数据的系数符号序列相关系数都较大。因此,医学体数据的全局三维DCT系数符号序列可以作为其视觉特征向量。
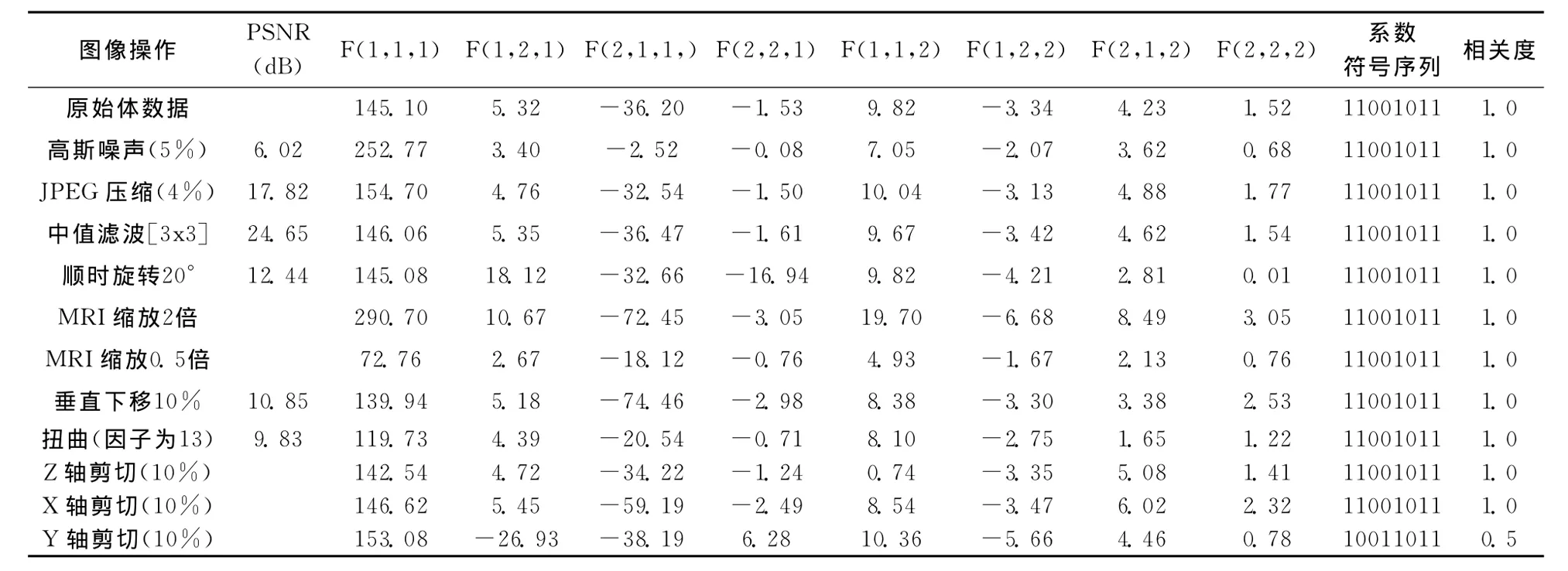
表1 医学体数据全局三维DCT变换低中频部分系数及受不同攻击后的变化值
2.2 多水印的混沌加密
步骤1 应用Logistic Map产生混沌加密矩阵。
由初始值x0生成混沌序列X(j)。由于多水印为二维图像,所以X(j)需要通过升维运算得到二维矩阵。最后,混沌序列X(j)通过符号运算得到二值加密矩阵C(i,j)。其中X(j)的值大于0.5的为 “1”,其余为 “0”。
步骤2 得到混沌加密的多水印。
首先,将原始多重水印转化为二值多重水印Wk(i,j),然后根据Hash函数性质,由二值加密矩阵C(i,j)和二值多水印Wk(i,j)得到混沌加密的多重水印BWk(i,j):BWk(i,j)=Wk(i,j)⊕C(i,j)。
2.3 多水印的嵌入与提取算法
步骤3 通过全局三维DCT变换,提取医学体数据的视觉特征向量。
先对原始医学体数据F(i,j,k)进行全局三维DCT变换,得到三维DCT系数矩阵FD(i,j,k),再将系数矩阵中的系数按照频率由低到高的顺序排列,从中选取前L个,并通过符号运算得到原始医学体数据的视觉特征向量
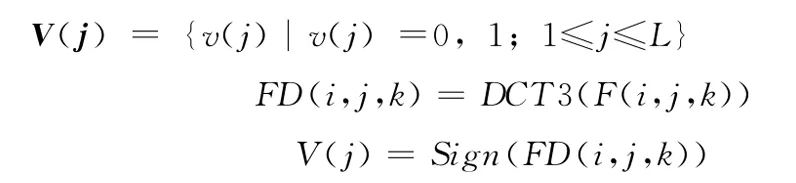
步骤4 嵌入混沌加密的多水印并得到二值逻辑密钥。
由提取的原始医学体数据的特征向量V(j)和混沌加密的多重水印BWk(i,j),通过密码学常用的Hash函数性质生成二值逻辑密钥Keyk(i,j)。保存Keyk(i,j),在后面提取水印时需要。将Keyk(i,j)作为密钥向第三方申请,以获得原始医学体数据的查看权和使用权。该算法多水印的嵌入没有改变原始医学体数据的体素数据值,是一种零水印方案
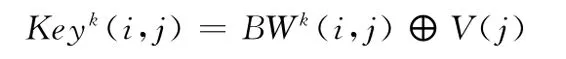
步骤5 提取经过攻击后的待测水印体数据的视觉特征向量。
设待测水印体数据为F’(i,j,k),经过三维DCT变换后得到的三维DCT系数矩阵为FD’(i,j,k)。按照上文步骤3的方法得到待测水印体数据的视觉特征向量
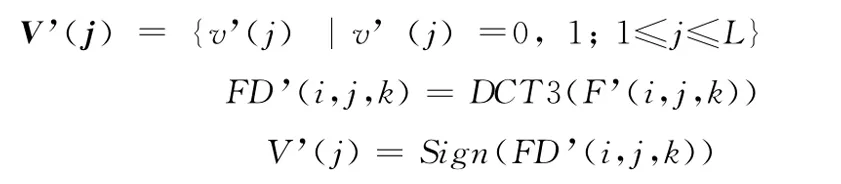
步骤6 利用Hash函数,提取待测水印体数据中的加密多水印

式中:V’(j)——提取的待测水印体数据的视觉特征向量,Keyk(i,j)——嵌入多水印时得到的二值逻辑密钥序列。通过Hash函数性质得到待测水印体数据中所含的多水印BWk’(i,j)。
2.4 还原提取的多重水印
步骤7 生成混沌序列并得到二值加密矩阵。
令初始值x0与上文步骤1中保持一致,通过Logistic Map得到相同的混沌序列X(j)和二值加密矩阵C(i,j)。
步骤8 利用二值加密矩阵还原提取的多水印。
由待测体数据中提取的多水印BWk’(i,j)和二值加密矩阵C(i,j),通过密码学中的Hash函数性质得到还原的多水印Wk’(i,j)
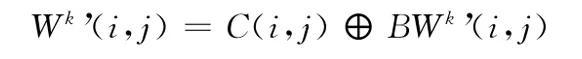
根据Wk(i,j)和Wk’(i,j)的相关程度,我们可以判断医学体数据中所含的水印,从而确定待测医学体数据的所有权,保护病患的个人信息。图1为鲁棒多水印算法流程图。由图1可以看出,该算法实现了零水印嵌入和水印的盲提取,提高了医学体数据的安全性。
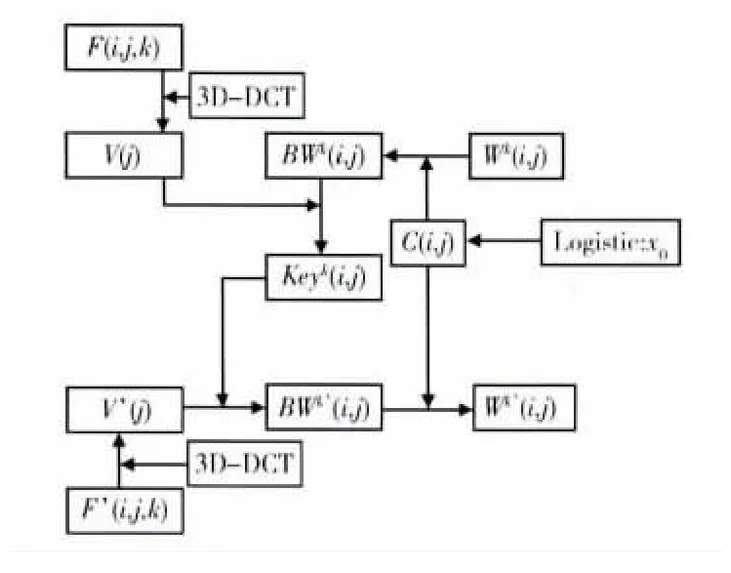
图1 鲁棒多水印算法流程
3 实验结果与抗攻击分析
仿真平台是Matlab2010a,选择两个有意义的图像作为嵌入医学体数据的多水印,如图2(a)-(b)所示,记为:Wk={wk(i,j)|wk(i,j)=0,1;1≤i≤32,1≤j≤32,k=1,2}。图2(c)-(d)是由Logistic Map混沌加密的多水印,从图中可以明显看到水印变得杂乱无章,安全性 提高。原始医学体数据见图3(a),表示为:F={f(i,j,k)|f(i,j,k)∈R;1≤i,j≤128,1≤k≤27}。实验中,Logistic Map初始值x0为0.2,增长参数μ为4。

图2 原始水印和加密的水印
通过水印算法检测出Wk’(i,j)后,通过计算Wk(i,j)和Wk’(i,j)的归一化相关系数NCk来判断是否有水印嵌入。本实验中用NC1、NC2分别表示与提取的两个水印对应的相关系数。其中归一化相关系数NC公式为

式中 :W(i,j)、W’(i,j)——嵌入的原始水印和提取的水印。NC值越大,说明嵌入的水印和提取的水印相关程度越高。

图3 不加干扰时的医学体数据及提取的多水印

图4 高斯噪声强度为5%的体数据及提取的多水印

表2 水印抗高斯噪声实验数据
不加外部干扰时的医学水印体数据如图3(a)所示,可以看出含有水印的医学体数据非常清晰。图3(b)是医学水印体数据的一个切片,提取的水印如图3(c)-(d)所示,有NC1=1.00,NC2=1.00,可以准确地提取水印。看出体数据切片出现严重的方块效应,PSNR=16.57dB。此时,对应的体数据三维成像与原始体数据相比发生了很大的变化,如图5(a)所示。观察图5(c)-(d),有NC1=0.93,NC2=0.93,提取的多水印与原始多水印基本保持一致。
下面通过具体的实验来判断该水印算法的鲁棒性。
3.1 常规攻击
3.1.1 加入高斯噪声
使用imnoise()函数对水印体数据进行高斯噪声干扰,当噪声强度为5%时,水印体数据切片已经变的模糊不清,如图4(b)所示。由图4(a)可以明显看到水印体数据整体三维轮廓已经很模糊,PSNR=6.02dB。此时,提取的多水印依然十分清晰,且有NC1=0.95,NC2=0.94,如图4(c)-(d)所示。
表2为水印抗高斯噪声实验数据,可以看到噪声强度高达25%时,PSNR降至0.07dB,有NC1=0.72,NC2=0.75,依然能够较为准确得提取出多水印。因此,该算法有很好的抗高斯噪声干扰能力。
3.1.2 JPEG压缩处理
采用体数据压缩质量百分数作为参数对含水印体数据进行JPEG压缩处理,(压缩质量为2%)。由图5(b)可以

图5 JPEG压缩质量为2%的体数据及提取的多水印
表3为水印抗JPEG压缩实验数据,由表中实验数据得到,该算法对JPEG压缩有较强的鲁棒性。

表3 水印抗JPEG压缩实验数据
3.2 几何攻击
3.2.1 旋转变换
对水印体数据顺时针旋转4度,此时水印体数据的PSNR为17.54dB,如图6(a)所示。图6(b)为顺时针旋转4度的体数据切片。此时,提取的多水印清晰,与原始多水印保持一致,有NC1=0.95,NC2=0.94。

图6 顺时针旋转4度的体数据及提取的多水印
表4为水印抗旋转攻击实验数据,当对水印体数据顺时针旋转35°时,信噪比变得很低,为11.33dB,仍然可以较为准确地提取出多水印,有NC1=0.88,NC2=0.87。由此得出,该水印算法有较强的抗旋转攻击能力。

表4 水印抗旋转攻击实验数据
3.2.2 平移变换
对水印体数据进行平移变换,水平左移15%时的水印切片如图7(b)所示,对应的三维体数据如图7(a)所示,PSNR=8.63dB。提取的多水印如图7(c)-(d)所示,NC1=1.00,NC2=1.00,可以准确得提取出多水印。
表5为水印抗平移变换实验数据,由表中数据可以看到,当水印体数据水平左移20%时,仍可准确得提取多水印。故该算法有好的抗平移变换能力。

图7 向左平移15%的体数据及提取的多水印
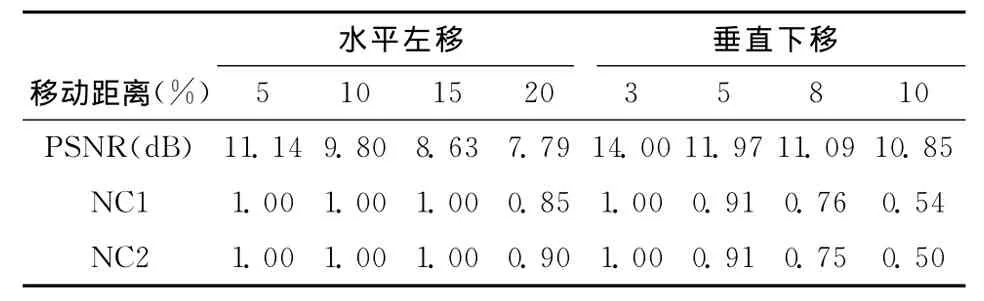
表5 水印抗平移变换实验数据
3.2.3 剪切实验
对水印体数据进行剪切实验,按Z轴方向剪切16%后,体数据三维成像的顶部已经缺失了很大一部分,如图8(a)所示。图8(b)为体数据的第一个切片图像。由图8(c)-(d)可以明显看到,多水印仍可被准确地提取出来,NC1=0.95,NC2=0.94。
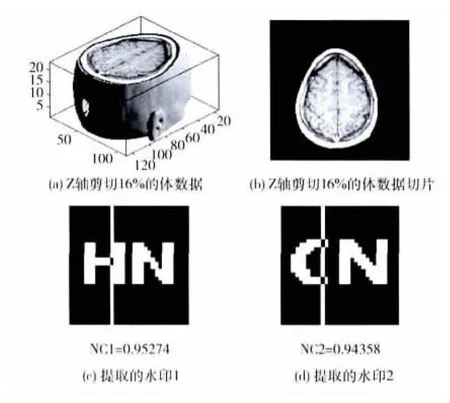
图8 Z轴剪切16%的体数据及提取的多水印
表6为水印抗剪切攻击实验数据,当水印体数据按Z轴方向剪切30%时,仍可有效地提取出多水印,有NC1=0.69,NC2=0.77。由此得知,本文所提出的算法有一定的抗剪切能力。

表6 水印抗剪切攻击实验数据
4 结束语
针对医学体数据水印信息的安全性保护,本文提出了一种基于三维DCT和混沌加密的医学体数据鲁棒多水印算法。
算法利用三维DCT变换提取医学体数据的视觉特征向量,通过视觉特征向量进行多重水印的嵌入与提取,结合第三方概念和Hash函数性质,实现了零水印嵌入和水印的盲提取,有效地保护了医学体数据。在多水印的处理上,采用了Logistic混沌映射对多水印进行加密,提高了水印信息的安全性。与此同时,该算法提高了嵌入体数据的水印容量,有更好的实用性。
实验结果表明,该算法可以有效地提取多水印,且对常规攻击和几何攻击都有很好的鲁棒性。
此外,该算法也可用于其它领域的三维体数据水印信息保护和认证。
[1]Bhargava N,Sharma M M,Garhwal A S,et al.Digital image authentication system based on digital watermarking[C]//Proc of the IEEE International Conference on Radar,Communication and Computing,2012:185-189.
[2]Feng Hongyu,Gu Yuesheng,Li Yancui.Research on digital watermarking based on wavelet theory[J].Journal of Convergence Information Technology,2012,7 (13):292-299.
[3]Kaur S,Farooq O,Singhal R,et al.Digital watermarking of ECG data for secure wireless communication[C]//Proc of the IEEE International Conference on Recent Trends in Information,Telecommunication and Computing,2010:140-144.
[4]Navas K A,Sasikumar M.Survey of medical image watermarking algorithms[C]//Tunisia:Proc of the 4th Sciences of Electronic,Technologies of Information and Telecommunications International Conference,2007:25-29.
[5]YE Tianyu,NIU Xinxin,YANG Yixian.A multi-purpose dual watermark algorithm[J].Journal of Electronics &Information Technology,2009,31 (3):546-551 (in Chinese).[叶天语,钮心忻,杨义先.多功能双水印算法[J].电子与信息学报,2009,31 (3):546-551.]
[6]Dong Chunhua,Li Jingbing,Han Xianhua,et al.Multiple watermarks for management in medical image based on DWT[J].International Journal of Digital Content Technology and its Applications,2012,6 (10):239-247.
[7]LIU Quan,JIANG Xuemei.Hierarchical semi-fragile digital watermarking algorithm for image tamper localization and recovery[J].Journal on Communications,2007,28 (7):104-110 (in Chinese).[刘泉,江雪梅.用于图像篡改定位和恢复的分层半脆弱数字水印算法[J].通信学报,2007,28 (7):104-110.]
[8]CHEN Haipeng,QIN Jun,SHEN Xuanjing,et al.Robust watermarking algorithm based on the feature of digital image[J].Computer Science,2011,38 (5):258-264(in Chinese).[陈海鹏,秦俊,申铉京,等.基于图像特征的鲁棒性数字水印算法[J].计算机科学,2011,38 (5):258-264.]
[9]CHEN Wufan,QIN An,JIANG Shaofeng,et al.Medical image analysis:State of the art and future directions[J].Chinese Journal of Biomedical Engineering,2008,27 (2):175-181(in Chinese).[陈武凡,秦安,江少峰,等.医学图像分析的现状与展望[J].中国生物医学工程学报,2008,27(2):175-181.]
[10]ZOU Changhua,TAN Shiheng,LIN Tusheng.Digital watermarking algorithm in DCT based on chaotic scrambling and chaotic encryption[J].Microelectronics &Computer,2011,28 (5):58-62 (in Chinese).[邹长华,谭世恒,林土胜.基于混沌置乱和混沌加密的DCT域数字水印算法[J].微电子学与计算机,2011,28 (5):58-62.]

