一类三次系统的细中心与局部临界周期分支

陈 挺，黄文韬，2，马皖川

(1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004;2.贺州学院 数学系，广西 贺州 542800)

1989年，C.Chicone 与M.Jacobs［1］类比N.Bautin［2］研究了小振幅极限环的方法，首次提出了k 阶细中心和局部临界周期分支(简称临界周期分支)的概念.在文献［1］中，作者证明了奇点的临界周期分支的一些定理，并研究了二次系统的临界周期分支情况.林怡平与李继彬［3］用复系统的方法研究了细中心和临界周期分支，解决了不含二次项的三次复系统的临界周期分支问题.文献［4-5］也研究了不含二次项的三次系统原点的临界周期分支问题.文献［6］给出了一类三次Kukles系统的原点最多有三个临界周期分支.张伟年等［7］讨论了一类三次可逆多项式系统的情形.另外，文献［8］也讨论了一类特殊的三次系统的临界周期问题.文献［9-10］研究了Hamilton 系统的临界周期问题.文献［11-12］研究了Lénard 系统的临界周期问题.对于临界周期分支相关问题的研究还可见文献［13-17］.

本文考虑如下一类三次系统原点的细中心和临界周期分支问题

系数Ai，j，Bi，j(i=0，1，2，3;j=0，1，2)是实数.

文献［18］研究了系统(1)的中心条件，本文将利用文献［19］定义的复自治系统的周期常数及递推公式，得到该系统原点的细中心阶数，并证明了该系统原点能分支出3 个临界周期分支.

1 预备知识

考虑系统

式中:λ ∈Λ.在原点充分小的邻域内，设P(h，λ)为系统(2)通过非零点(h，0)的闭轨的最小周期函数.由文献［1］得，P(h，λ)是局部可积的，其泰勒展开式为

对正整数k，如果存在λ*∈Λ，使得P2(λ*)=…=P2k(λ*)=0，P2k+2(λ*)≠0，则系统(2)的原点为k 阶细中心(当k=0 时称为粗中心);如果对任意的正整数m，都存在P2m=0，则原点为系统的等时中心.对于局部临界周期分支有如下定义:

定义1 对于参数λ*∈Λ，系统(2)的原点为细中心，如果存在ε0＞0，使得任意0 ＜ε ＜ε0和每一个λ*的充分小邻域W，存在一个λ1∈W，使得P'(h，λ1)在U=(0，ε)内有k 个解，则称在λ*系统原点有k 个局部临界周期分支.

定义2 考虑有限个函数的集合fi∶RN→R，i=1，2，…，l.记

称f1，f2，…，fl相对于f 在λ*∈V(f1，f2，…，fl)是无关的.如果

(i)λ*的任意邻域包含一个λ ∈V(f1，f2，…，fl)，使得fl(λ)f(λ)＜0;

(ii)对于变量V(f1，f2，…，fl)，2 ≤j ≤l -1，存在λ ∈V(f1，f2，…，fj)，fj+1(λ)≠0，且λ 的任一邻域W 都包含一个σ ∈V(f1，f2，…，fj-1)，使得fj(σ)fj+1(λ)＜0;

(iii)若λ ∈V(f1)，f2(λ)≠0，则λ 的任一个邻域W*都包含一个σ，使得f1(σ)f2(λ)＜0.

显然，若f1，f2，…，fl相对于f 在λ*∈V(f1，f2，…，fl)是无关的，则任意λ ∈V(f1，f2，…，fk-1)使得fk(λ)≠0 时，对于每一个k=1，2，…，l，f1，f2，…，fk-1相对于fk是无关的;且若▽f1(λ*)，…，▽fl(λ*)，▽f(λ*)是线性无关，则f1，f2，…，fl在λ*下相对于f 是无关的.

引理1 设系统参数为λ*时，系统(2)的原点是一个k 阶细中心，则至多有k 个临界周期从原点分支出来;并且，若原点的周期常数P2，P4，…，P2k在λ*下相对于P2k+2是无关的，则对于满足m≤k 的任意正整数m，恰好有m 个临界周期分支.

从文献［19］的定理5.4 可知，系统(2)原点的第一个非零周期常数P2k与其共轭复系统原点的第一个非零复周期常数τk满足如下关系:

假设复周期常数τi由k 个线性无关的参数a1，a2，…，ak组成，即τi=τi(λ)=τi(a1，a2，…，ak).由文献［10］的定理2 可以得到如下定理证明局部临界周期存在的充分条件.

定理1 当存在λ*=(a1c，a2c，…，akc)时，使得

则通过λ=λ*的小扰动，系统(2)恰有k 个局部临界周期分支.

2 细中心与局部临界周期分支

通过变换

把系统(1)变换成它的伴随复系统

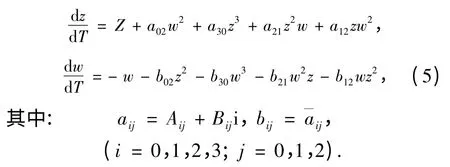
记λ=(a30，b30，a21，b21，a12，b12，a02，b02)∈C8，根据文献［18］中的定理4，可以得到系统(1)原点为中心的充要条件如下:

引理2 系统(1)的原点为中心(伴随复系统(5)的原点为复中心)，当且仅当λ ∈K1∪K2∪K3，其中:

结合文献［19-20］给出求系统周期常数的递推算法，下面分别讨论系统(1)原点在三种中心条件下的细中心条件及临界周期分支的情况.

情形1 中心条件K1成立.把a21=b21，b12=3a30，a12=3b30代入文献［19］中的递推公式进行计算，可得系统(5)的前3 个复周期常数为

其中:在上述τk的计算过程中，已置 τ1=…=τk-1=0 (k=2，3).由上可以得到前3 个周期常数都为零，当且仅当下列条件成立:

且当λ ∈S1时，系统(5)变为了线性型系统，所以其原点为复等时中心.相应地，系统(1)的原点为等时中心.当0 时，τ1=τ2=0，τ3≠0.因此，在λ ∈K1时，系统(1)的原点至多是2 阶细中心，并得到以下结论:

定理2 当λ ∈S1时，系统(1)的原点为等时中心.

定理3 当λ ∈K1时，系统(1)的原点至多是2 阶细中心，而且原点是k(k=0，1，2)阶细中心，当且仅当λ ∈其中:

定理4 如果λ*∈，在λ*下系统(1)在原点没有临界周期分支;如果λ*∈(k=1，2)，在λ*下系统(1)的原点至多有k 个临界周期分支，且对于任意正整数m(0 ≤m ≤k)，系统的原点恰好有m 个临界周期分支.

证明 定理4 的前半部分可根据引理1 直接得到，对于定理4 的后半部分，这里只做k=2 情形的证明.对任一λ*∈，需要证明P2，P4相对于P6是无关的.

设任意λ*∈即

对λ*的任一满足的领域W，在其内可找到一点

其中:ε ＞0 充分小，sign(x)表示符号函数.则有原点的周期常数满足

因此，定义2 的条件(i)成立.

下面设

对于λ 的任一满足的领域W'，存在

因此，定义2 的条件(iii)成立.证毕.

情形2 中心条件K2成立.把中心条件代入文献［19］中的递推公式进行计算，可得系统(5)的复周期常数，并化简得到

1)当a30=b30=0 时，

由上可以得到前3 个周期常数都为零，当且仅当条件λ ∈S1.当时，有τ1=τ2=0，τ3≠0，则系统(1)的原点至多是2 阶细中心.

借助Mathematica 软件计算理想〈F1，F2〉的Groebner 基，有

从而得到F1=0 与F2=0 没有公共实根，所以当F1=0，a30b30≠0 时，有τ3=0，τ4≠0.因此，在λ ∈K2时，系统(1)的原点至多是3 阶细中心，并得到以下结论:

定理5 当λ ∈K2时，系统(1)的原点至多是3 阶细中心，而且原点是k(k=0，1，2，3)阶细中心，当且仅当λ ∈其中:

定理6 当λ*∈)时，系统(1)在λ*下原点最多存在k 个局部临界周期分支.而且在λ*下，对任意的正整数m(0 ≤m ≤k)，恰好有m 个临界周期从原点分支出来.

证明方法与定理4 的相同，只需要证明P2，P4，P6相对于P8是无关的，在此不再做证明.下面应用定理1 直接证明在K32 条件下，系统(1)的原点邻域恰有3 个临界周期分支.通过计算Jacobian行列式，由a30b30≠0 和333 +853q +412q2=0 可知

情形3 中心条件K3成立.把a21=b21=0，a12+b30=b12+a30=0 代入文献［19］中的递推公式进行计算，可得系统(5)原点的周期常数为

由上述可得，当a02=b02=0 时，τ1=τ2=τ3=…=0，该条件满足文献［21］中定理5 的条件三，故系统(1)的原点为等时中心;若a02b02≠0，则有τ1≠0，故系统(1)的原点是一个粗中心，系统原点邻域没有临界周期分支.

定理7 当λ ∈S2时，系统(1)的原点为等时中心，其中:

定理8 如果λ*∈系统(1)的原点为一个粗中心，且在λ*下系统(1)的原点没有临界周期分支，其中:

［1］Chicone C，Jacobs M.Bifurcation of critical periods for plane vector fields［J］.Amer.Math.Soc.Trans.，1989，312:433-486.

［2］Bautin N N.On the number of limit cycles which appear with the variation of coefficients from an equilibrium position of focus or center type［J］.American Math.Soc.，1954，19MR 15:527.

［3］林怡平，李继彬.平面自治系统的规范型与闭轨族周期的临界点［J］.数学学报，1991(34):490-501.

［4］Rousseau C，Toni B.Local bifurcation of critical periods in vector fields with homogeneous nonlinearities of the third degree［J］.Canad.Math.Bull.，1993，36(4):473-484.

［5］Romanovski V G，Han M A.Critical period bifurcations of a cubic system［J］.J Physics A:Math.General.，2003，36(18):5011.

［6］Rousseau C，Toni B.Local bifurcations of critical periods in the reduced kukles system［J］.Can.J.Math.，1997，49:338-358.

［7］Zhang W N，Hou X R，Zeng Z B.Weak centers and bifurcation of critical periods in reversible cubic systems［J］.Comput.Math.Appl.，2000，40(6):771-782.

［8］Chen X W.Decomposition of algebraic sets and applications to weak centers of cubic systems［J］.J.Comput.Appl.Math.，2009，232(2):565-581.

［9］Mañosas F，Villadelprat J.A note on the critical periods of potential systems［J］.Int.J.Bifurcation and Chaos，2006，16(3):765-774.

［10］Yu P，Han M A，Zhang J H.Critical periods of thirdorder planar hamiltonian systems［J］.Int.J.Bifurcation and Chaos，2010，20:2213-2224.

［11］Zou L.Local bifurcations of critical periods for cubic Lénard equations with cubic damping［J］.J.Comput.Appl.Math.，2008，222:404-410.

［12］Xu Q J，Huang W T.The center conditions and local bifurcation of critical periods for a Lénard system［J］.Appl.Math.Comput.，2011，217:6637-6643.

［13］Gasull A，Zhao Y.Bifurcation of critical periods from the rigid quadratic isochronous vector field［J］.Bull.Des.Sci.Math.，2008，132(4):292-312.

［14］Cima A.On the number of critical periods for planar polynomial systems［J］.Nonl.Anal.:Theory Meth.Appl.，2008，69(7):1889-1903.

［15］Chicone C，Dumortier F.Finiteness for critical periods of planar analytic vector fields［J］.Nonl.Anal.，1993，20(4):315-335.

［16］De Maesschalck P，Dumortier F.The period function of classical Liénard equations［J］.J.Diff.Equa.，2007，233(2):380-403.

［17］Gasull A，Yu J.On the critical periods of perturbed isochronous centers［J］.J.Diff.Eqs.，2008，244(3):696-715.

［18］刘一戎.一类三次系统的奇点量公式和可积性条件，M(3)≥7［J］.科学通报，1989(17):1299-1301.

［19］黄文韬.微分自治系统的几类极限环分支与等时中心问题［D］.长沙:中南大学，2004.

［20］Liu Y R.A new method to determine isochronous center conditions for polynomial differential systems［J］.Bull.Des Sci.Math.，2003，127:133-148.

［21］Han M A，Romanovski V G.Isochronicity and normal forms of polynomial systems of ODEs［J］.J.Symb.Comput.，2012，47:1163-1174.