基于PSO粒子滤波的弹道目标跟踪方法

王 芳，赵捍东，曹红松，张建锋

(1.中北大学 机电工程学院，山西 太原 030051;2.中国人民解放军75753 部队，广东 广州 510600)

0 引言

弹道跟踪技术是对火炮和火箭弹道进行观测、评估、校射的关键.但实际使用情况是，由于观测设备本身的误差和其他随机因素的影响，使得测量到的飞行数据与当前真实的飞行数据并不完全相符［1-2］.为了对弹道进行准确的跟踪，就需要对当前的观测值进行相应的滤波处理.刘也和徐明友［2-3］采用了卡尔曼滤波算法进行了弹道的跟踪，但其跟踪模型均建立在离散线性系统的基础上，而且未考虑复杂噪声的影响.文献［4-8］提出了一种基于粒子滤波的目标跟踪方法，但对可能发生的粒子贫乏问题却未做改进，且均是讨论在二维弹道上进行跟踪，而随着采样次数的增加，粒子贫乏将会极大地影响跟踪效果.为此本文提出一种基于改进型粒子滤波的弹道目标跟踪预测方法.

1 粒子滤波原理

粒子滤波是一种新兴的非线性滤波算法［4］，其进行滤波实现的基本思路是:首先依据系统状态向量的经验条件分布，在状态空间内生产随机样本集合，则这些样本就被称为粒子;然后根据观测值不断地修正“粒子”的权重和位置，即样本的比重和样本值;再通过调整后的“粒子”的信息，修正最初的经验条件分布.事实证明，当样本数足够大时，这种估计就无限接近于真实后验概率密度［8-9］.直观地说，就是寻找一组在状态空间中传播的随机样本对样本对应的概率密度函数p(xk|zk)进行近似，从而获得状态的最小方差估计.其使用范围不限于线性系统和高斯噪声环境，因此该方法广泛应用于自动控制、导航、制导等领域.

对于弹道跟踪与预测问题，不失一般性，假设观测系统的非线性状态系统为

式中:xt表示t 时刻的状态量;yt表示t 时刻的观测量;ft，ht表示t 时刻的状态转移函数和观测函数;vt，nt表示t 时刻的状态噪声和观测噪声向量.假设状态的初始概率密度函数p(x0|y0)=p(x0)为已知，那么状态的预测量就可以经贝叶斯递推表达为

状态量的观测更新为

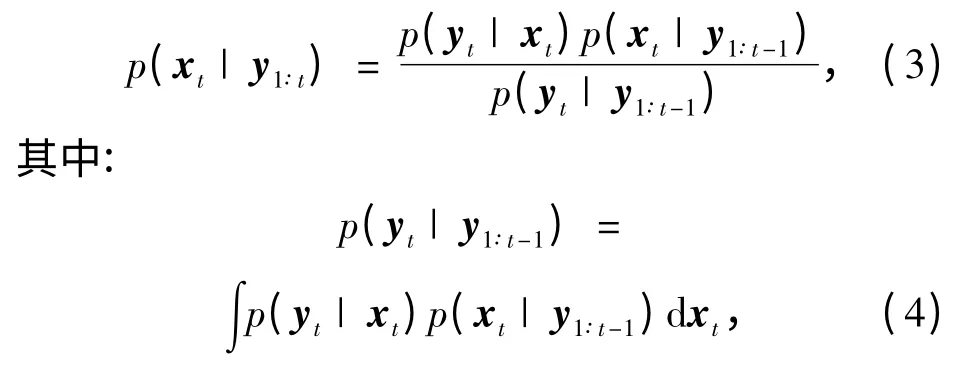
式中:y1∶t={y1，y2，…，yt}.

显然，式(2)～(4)中的积分运算会给解算带来诸多不便，不利于实现p(x0∶t|y0∶t)的递推，为此粒子滤波引入了Monte Carlo 积分方法［10-12］.假设采集到N 个独立分布的样本，那么状态的后验概率可近似地表示为

根据大数定律可以证明，当粒子数和采样频率足够大时，通过蒙特卡洛积分方法获得的估计量，可以无限逼真实状态.由于目标密度函数p(x)实际上往往比较复杂，所以从中获取粒子权值是比较难实现的，于是工程中常使用重要性密度函数进行采样，可将这个重要性密度函数表达为q(x0∶t|y1∶t)，并且q(x0∶t|y1∶t)需包含p(x0∶t|y1∶t)所有的支承点集.重要性密度函数的求取方法为［8-9］

式中:w 表示对应于样本的权值.

同时定义

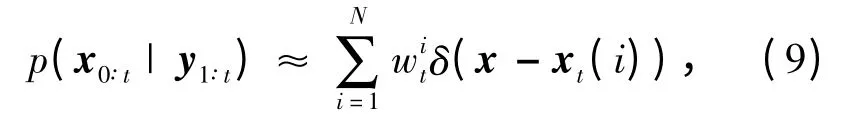
从而可以得到状态的估计值为

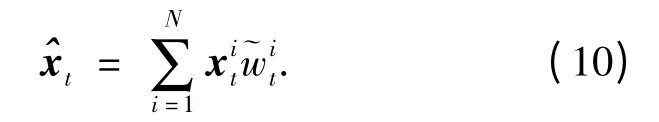
从上述可以看出，粒子滤波过程没有噪声为高斯噪声的限制，因此其应用范围得到了很大的扩展，为复杂噪声条件下的弹道目标跟踪提供了一种手段.

2 跟踪预测模型

在飞行过程中，弹丸的动力学模型具有典型的非线性特征，受到诸多空气动力的作用，运动情况复杂［3］，雷达的跟踪角度无法做到完全精确，同时雷达观测信号具有厚尾噪声和随机噪声.在基于贝叶斯概率滤波的框架下，飞行跟踪问题可以转化为最大后验概率估计的过程，易知飞行跟踪问题符合马尔可夫过程，即认为仅有前一时刻的状态量对当前状态量有影响.

首先需要对飞行过程建立离散的空间状态模型，结合空气动力学，取状态变量

式中:Xt为t 时刻的状态变量;分别为t 时刻沿三个垂直方向的位置分量、速度分量和阻力系数.令

那么式(1)中的状态转移方程可转化为

式中:T 为采样间隔.跟踪的观测量为雷达数据中的向径r，方向角β，高低角ε 三个量［3］，如图1 所示.

图1 地面观测弹丸示意图Fig.1 Schematic of ground observation projectile

结合图1 中所示的雷达观测位置，可得观测向量与状态向量表达方式之间的转换关系为

那么观测模型就可以表达为离散形式

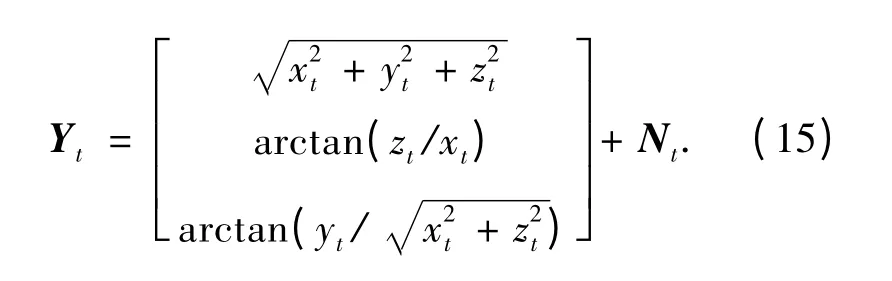
建立状态转移模型和观测模型之后，即可初始化采样粒子.根据式(13)的状态转移函数获得初步预测的概率密度，而后根据式(15)获得似然函数.通过观测值，根据式(3)修正先验信息，获得相应的后验概率，即进行后验估计.每观测一次，即可进行一次递推，其实质就是在得到观测向量yt以后估算状态向量xt的相应值，即得到式(10)的值.

3 重采样改进

经典粒子滤波算法的重采样过程为SIS 过程，而SIS 采样算法将导致粒子贫乏，即描述真实状态的粒子在多步采样后多样性逐渐变差，这对于准确跟踪是非常不利的.在粒子重采样的过程中保持粒子的多样性，是进行准确跟踪的关键，为此很多学者提出了多种改进方案［13-14］.为了获得准确的跟踪精度，本文采用了基于粒子群优化的方法来优化重采样过程的方法.粒子群优化的基本原理为

式中:wmax表示初始权重;wmin表示最终权重;k 表示当前迭代次数;kmax表示最大迭代次数.将此方法用于粒子滤波重采样时，其目的在于使得粒子运动到真实位置附近，则这些粒子就可以认为是滤波中采集的样本，即粒子.而粒子的当前位置就可以认为是各采样样本当前状态量的值，即

可以认为其为一多维向量，而找到的最优“位置”即为对向量中的元素的最优解.事实上，任何一种算法都不是完美的，粒子群算法有着对环境不敏感、易早熟等问题［15-16］.为了利用粒子群算法的优点，且避开其典型缺陷，本文使用种群小生境粒子群算法，并对式(5)做了如下改进:

式中:pbest 表示自身极值;gbest 表示全局极值;η 表示最大搜索范围;其他符号与式(5)中相同.

为了度量种群的进化程度，定义如下式子:

式中:f 表示第k 次迭代时的最优粒子适应度;Rk表示第k 步的滤波方差;ynew表示观测量的新的观测值;ypred表示观测量的预测值.同时定义一个大于0 的数ε，则当f ＞ε 时表示此种群正在进化，否则表示此种群已经成熟，并取出最优个体.那么当改进的粒子群算法用于优化重采样时，其基本思想为:首先初始化权值阈值信息作为粒子群的初始值，对初始值按照式(19)进行迭代计算，并计算出每个粒子的自身最优位置和群体最优位置，然后逐次迭代，直到得出最优的权值和阈值，即取出最优个体，那么最优粒子即是最接近真实状态的样本量.小生境粒子群优化算法优化样本(粒子)重采样过程的流程如图2 所示.

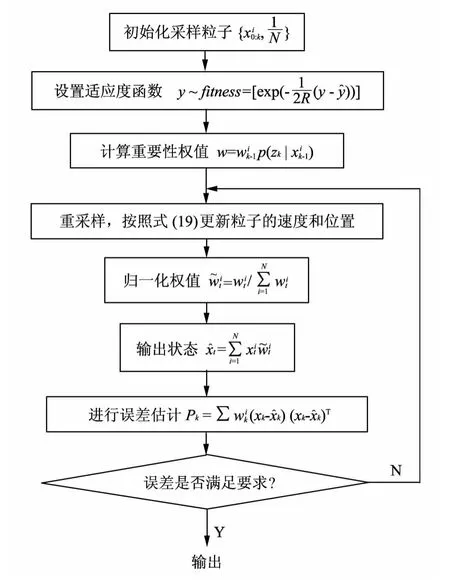
图2 粒子群优化粒子滤波算法流程图Fig.2 PSO optimization particle algorithm flowchart

4 仿 真

为了验证本文方法的有效性，对某型155 mm弹丸的弹道进行了跟踪仿真，在初速930 m/s，射角50° 的一条弹道加入由高斯噪声和厚尾噪声构成的复杂噪声，噪声均值为0，方差为20，最小值为0，最大值为75，仅对弹道的位置量加入噪声.从弹丸飞行高度为1 000 m 时开始跟踪弹道数据，飞行至弹丸高度为10 000 m 时结束跟踪，每0.5 s采集一次飞行数据.分别采用传统的卡尔曼滤波方法和本文提出的粒子群优化粒子滤波算法进行弹道跟踪.统计真实弹道和加入噪声后的观测弹道，以及基于卡尔曼滤波的跟踪弹道和基于本文方法的跟踪弹道，并对弹丸位置的跟踪效果进行比较，如图3 所示.

分别对两种算法在弹道目标跟踪时得到的位置误差进行统计，并与观测误差进行比较，如图4所示.从图4 中可以看出，基于卡尔曼滤波的跟踪效果与观测噪声相比有很大程度的改善，但滤波后依然有较大的误差存在.基于本文方法的跟踪精度比卡尔曼滤波方法提高了50%左右.

图3 全弹道范围跟踪效果Fig.3 The whole ballistic tracking result

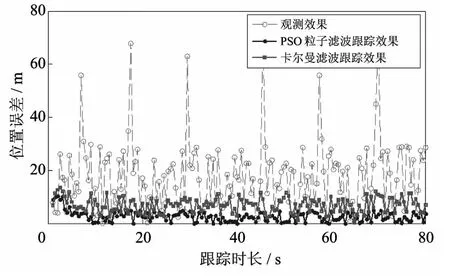
图4 弹道跟踪位置误差统计Fig.4 The position error statistic of whole ballistic tracking

除了位置跟踪外，速度跟踪和加速度跟踪是弹道跟踪的重要内容，其实质即为在滤波得到弹丸位置数据的基础上，经过对时间的求导，获得速度信息和加速度信息.统计两种方法对速度和加速度的跟踪效果，如图5 和图6 所示.

图5 弹道跟踪速度误差统计Fig.5 Ballistic tracking error statistic of velocity

从图4～图6 可以看出，在复杂噪声的情况下，卡尔曼滤波方法虽然可以在很大程度上减小噪声的影响，但总的滤波效果有限.而本文提出的PSO 粒子滤波方法可以有效地抑制复杂噪声的影响，经过PSO 粒子滤波处理，位置误差的均方差下降到3 m，速度误差的均方差下降到2 m/s，加速度误差总体下降到0.1 m/s2以内.

图6 弹道跟踪加速度误差Fig.6 Ballistic tracking error of acceleration

5 结束语

为了在观测设备具有复杂噪声的情况下获得良好的弹道跟踪效果，本文提出了一种基于小生境粒子群优化粒子滤波的弹道目标跟踪方法.通过粒子群优化粒子滤波的重采样过程，获得了较高精度的当前状态值.仿真结果表明:PSO 粒子滤波的弹道目标跟踪精度优于经典卡尔曼滤波，在此基础上对速度和加速度的跟踪效果也均优于卡尔曼滤波方法，为复杂噪声条件下弹道跟踪的实际应用提供了一种参考.

［1］de Campos Ferreira J C B，Waldmann J.Covariance intersection-based sensor fusion for sounding rocket tracking and impact area prediction［J］.Control Engineering Practice，2007(15):389-409.

［2］刘也.弹道目标实时跟踪的稳健高精度融合滤波方法［D］.长沙:国防科学技术大学，2011.

［3］徐明友.高等外弹道学［M］.北京:高等教育出版社，2003.

［4］程水英，张剑云.粒子滤波评述［J］.宇航学报，2008，29(4):1099-1111.Cheng Shuiying，Zhang Jianyun.Review on particle filters［J］.Journal of Astronautics，2008，29(4):1099-1111.(in Chinese)

［5］Cheng C，Ansari R.Kernel particle filter for visual tracking［J］.IEEE Signal Processing Letters，2005，12(3):242-245.

［6］Arasaratnam I，Haykin S，Elliott R J.Discrete-time nonlinear filtering algorithms using gauss-hermite quadrature［J］.Proceedings of the IEEE，2007，95(5):953-977.

［7］刘彦伟，张绍武，赵慧波，等.IMM-EKF 的弹道导弹轨道实时动态预测［J］.火力与指挥控制，2012，37(3):26-30.Liu Yanwei，Zhang Shaowu，Zhao Huibo，et al.The dynamic prediction of ballistic missile trajectory in real time based on IMM EKF［J］.Fir Control ＆ Command Control，2012，37(3):26-30.(in Chinese)

［8］徐长爱，李尚生，殷勇，等.基于粒子滤波的飞行目标跟踪［J］.电光与控制，2008，15(10):81-84.Xu Changai，Li Shangsheng，Yin Yong，et al.Ballistic object tracking based on particle filter［J］.Electronics Optics ＆ Control，2008，15(10):81-84.(in Chinese)

［9］陈志敏，薄煜明，吴盘龙，等.基于新型粒子群优化的粒子滤波雷达目标跟踪算法［J］.信息与控制，2012，41(2):413-418.Chen Zhimin，Bo Yuming，Wu Panlong，et al.A particle filter radar target tracking algorithm based on novel particle swarm optimization［J］.Information and Control，2012，41(2):413-418.(in Chinese)

［10］Gustafsson F，Bergman N.Particle filters for positioning，navigation，and tracking［J］.IEEE Transactions on signal processing，2002，50(2):425-437.

［11］Liu Huaping，Sun Fuchun.Efficient visual tracking using particle filter with incremental likelihood calculation［J］.Information Sciences，2012，195:141-153.

［12］张焱，沈振康，乔士东.一种改进型的粒子滤波器［J］.信号处理，2008，24(1):58-61.Zhang Yan，Shen Zhenkang，Qiao Shidong.An improved particle filter［J］.Signal Process，2008，24(1):58-61.(in Chinese)

［13］Jing W，Zhao H，Song C H，et al.A optimized particle filter based on PSO algorithm［C］.Sanya:Int Conf on Future BioMedical Information Engineering，2009:122-125.

［14］Clerc M，Kennedy J.The particle swarm:explosion，stability，and convergence in multi-dimensional complex space［J］.IEEE Transaction on Evolutionary Computation，2012，6(1):58-73.

［15］Zhao Jing，Li Zhiyuan.Particle filter based on particle swarm optimization resampling for vision tracking［J］.Expert Systems with Applications，2010，37:8910-8914.

［16］Cheng Wenchang.PSO algorithm particle filters for improving the performance of lane detection and tracking systems in difficult roads［J］.Sensors，2012(12):17168-17185.