一种基于短LT码的级联编译码算法

黄晓可 刘洛琨 郭 虹

（解放军信息工程大学信息系统工程学院，郑州，450002）

引 言

数字喷泉码［1］是一种新颖的基于图的纠删编码技术，具有优良的抗删除特性，在删除信道中有着比其他码更好的应用前景。M.Luby于1998年提出了喷泉码的概念，并在2002年提出了第一种高效可行的喷泉码，即LT（Luby transform）码［2］。之后，Shokrollahi等人提出 Raptor码［3］，其中一种系统Raptor码已被3GPP的多媒体广播多播业务采用［10］。

LT码等最早都是为删除信道设计的，如今已经从有线走向了无线，并被推广到越来越多的领域，比如无线多媒体广播和深空通信［4－7］等。通常喷泉码码长需要达到103或更高量级才能取得良好的性能［8－9］，但是码长较长将导致译码时延和接收缓存较大。针对多媒体广播的实时性需求和深空通信中设备小型化与资源受限的特点，短码长喷泉码的研究具有重要现实意义［10－12］。

本文提出了一种码长在102量级的短LT码与传统纠错码的级联方案，利用Reed Solomon码与卷积码的强纠错检错能力，构造等效删除信道。针对方案所用LT码码长较短的特点，本文将置信传播（Belief propagation，BP）算法与高斯消元（Gauss elimination，GE）算法合并作为译码方法，同时分析比较了几类现有度分布对短LT码的适用性，最后对级联方案的纠错能力进行了仿真验证。理论分析和仿真证明了该方案的有效性，级联系统在等效包删除概率不超过0.01时，译码开销约为0.12。

1 短LT码与RS－CC码级联方案

级联系统的原理框图如图1所示，对于实时性要求较高的传输系统可选用短LT码，图1中二进制信源被等长度分组，每个原始数据分组的长度设为l，l的大小按RS编码需求长度设计。LT码以数据分组为单位，每k个原始数据分组进行一次LT编码，即每次LT编码前数据长度为k×l比特，编码后分组个数为K，数据长度为K×l比特，K值大小由等效信道的删除概率决定。

图1 LT码与RS码级联系统Fig.1 Concatenated system diagram of LT codes and RS codes

LT编码后，各数据分组分别进行RS－卷积（Reed solomon－convolution coding，RS－CC）编码。RS－CC码是一类传统的前向纠错编码方法。它由Reed Solomon码、交织编码和卷积码级联而成。卷积码有较强的纠随机错误能力，但是如果在解码过程中发生错误，解码器的Viterbi译码可能导致突发错误，为了降低出现突发错误长度超出RS码纠错范围的概率，在RS码与卷积码之间加入了块交织，交织编码的优点是不增加附加的监督码元且提高了抗突发误码的能力。

RS码同时具有检错和纠错的能力，在误比特率超出RS码纠错范围时，仍可被RS码较大概率地检测出来。文献［4］对RS－CC级联码的译码差错概率作了详细分析，硬判决后的Viterbi译码的比特差错概率上边界为

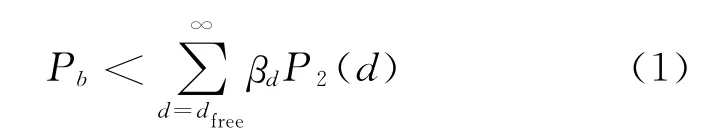
式中：dfree为卷积码的自由距离上边界；P2（d）为成对差错概率，因调制解调技术的不同而不同。在只有随机错误的情况下，有m个错误的概率为

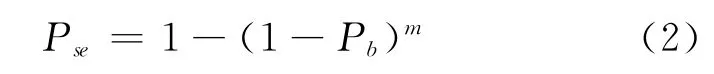
对于RS（n，l）码，信息符号长度为l，编码符号长度n≤2m－1，则其可纠错长度为即如果在一个编码符号内出现的错误数少于t个，则RS码可正确纠错，那么出现RS码不可纠的错误概率为

由于RS码可以检测出个数低于2t的错误，即出现RS码不可检的错误概率极低，因此可以将经过RS－CC级联码译码后的数据分为正确接收和检测出错误两类。RS－CC译码器检测并删除错误数据分组，只把正确数据分组传递给LT译码器，这样就将信道等效为删除信道，删除概率p＝Ppe，其中0≤p≤1。

K个编码数据分组经过删除概率为p的等效信道后，LT译码器收到K′＝K（1－p）个数据分组，然后运用适当的译码方法重构出k（k≤K′）个原始数据分组。可见，设计一种低复杂度且译码成功率高的LT码编译码算法是本方案的关键。级联方案确定后，通过改变喷泉码的输出分组个数k，若接收端接收到足够多正确的LT编码数据分组，可达到极低的误码率。

2 短LT码编译码算法与度分布函数设计

2.1 LT码编译码原理与算法

2.1.1 LT码编码

文献［2］对LT编码方法进行了详细的介绍分析，本文沿用了其中的一些定义与表示符号，假定原始数据长度为N，将其分为k组，则每个分组长度为l＝N／k，这些分组称为原始数据分组。由原始数据分组通过编码运算产生编码分组。LT码每个编码分组的产生过程如下：

（1）从给定度分布ρ（·）中随机产生一个度d。

（2）从k个原始分组中等概随机选取d个分组。

（3）将选取的d个分组进行异或运算，即得到一个编码分组。

（4）重复以上步骤即可源源不断地产生编码分组。

2.1.2 LT码译码

LT译码是对接收到的K′个编码分组进行处理来恢复出k个原始数据分组，一般要求K′略大于k。在删除信道中，对线性码的最大似然译码等同于解线性方程组，因此可以使用高斯消元算法来求解。对于给定的k个原始数据分组可用向量x＝ （x1，x2，…，xk）T表示，接收到的K′个编码分组可用向量y＝ （y1，y2，…，yK′）T表示。则整个译码过程可以视为用K′个方程联合求解k个未知数的一个线性方程组

式中：H为经过删除信道后的生成矩阵；hm为矩阵H第m列构成的列矢量，加法均为模2加运算。

但是，GE算法类似于矩阵求逆，在原始分组数k较大时运算量过大。因此，喷泉编码常采用置信传播迭代译码算法。

根据模2加的性质，则式（4）可以改写为

BP算法即是从矩阵H中找出一个重量为1的行，假设为第i行且该行唯一元素在第j列，则可直接得到yi＝xj，即xj被译出。则式（5）可写为

即

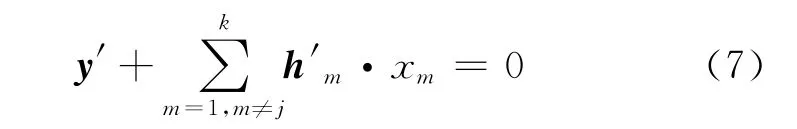
式中：编码分组集y更新为y′＝y＋hj·xj，矩阵H的第j列元素更新为全零，设为H′。因此，只要矩阵H′存在重量为1的行，以上过程就可以循环迭代进行。

2.1.3 译码算法分析与改进

GE算法译码运算量O（Kk2）随着原始数据分组个数的增加快速增长，而BP译码算法复杂度仅为O（klogk），实现简单。但BP算法的迭代过程容易因某一步没有解出新的数据就提前中止，导致无法完整译码。因此，采用BP算法时需要接收更多的编码分组以保证译码成功，而对于码长较短的喷泉码，BP算法的译码开销更大。对此，文献［8］提出了增强型高斯消元算法，但复杂度仍较高。文献［9，11］提出BP算法译码失败时可用其他算法求出一个新解继续进行迭代。

由于本文码长较短，将文献［9］的思想简化，提出置信传播高斯消元（Belief propagation Gauss elimination，BPGE）译码算法，即在BP译码失败时即对剩余未解出的分组全部采用GE译码，可以在保证与GE算法有相同译码成功率的条件下降低译码复杂度。

译码器首先采用BP算法译码，假设由于随机性的存在，在某次迭代之后矩阵H′中找不到重量为1的行，BP算法将被迫中止，此时剩余的方程即式（7）可写为

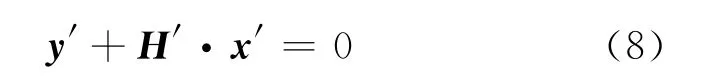
式中：x′为尚未译出的初始分组集合。

如果矩阵H列满秩即rank（H）＝k，即方程（5）有唯一解，则对应式（8）仍存在唯一解，此时，再采用高斯消元法求解式（8）。但是，如果rank（H）＜k，则说明译码失败，采用GE算法译码也无法求解，需要继续接收编码分组。可见，相对于直接用GE算法求解式（4），本文所提算法降低了复杂度且与GE算法有相同译码成功率。

2.2 度分布函数设计

在编码过程中，度分布函数的设计至关重要，好的度分布设计可以使得接收端用尽可能少的接收符号和尽可能小的复杂度恢复出原始信息。

2.2.1 常用度分布函数

文献［2］中给出了Ideal Soliton分布函数定义

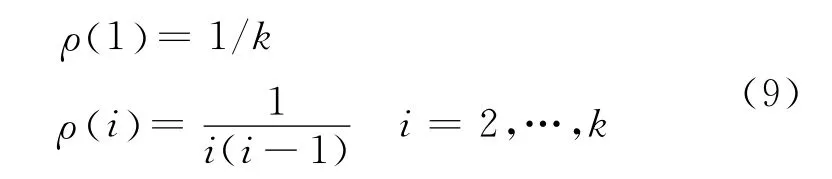
在此基础上，Robust Soliton分布引入了两个调节参数c和δ，其中，c为一大于零的可调常数，δ则与译码错误概率有关。定义

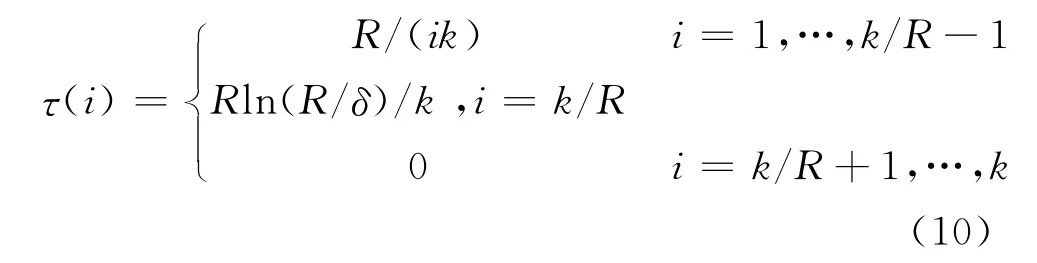
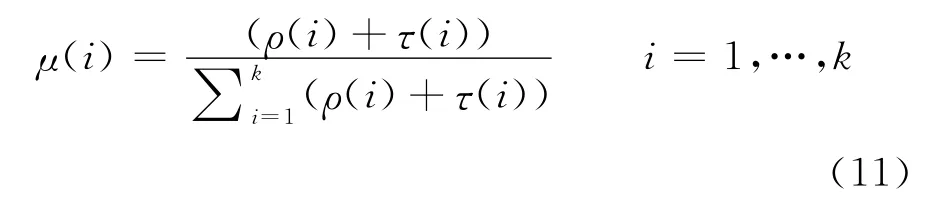
除了以上两种经典分布外，较著名的已被3GPP组织的多媒体广播多播业务标准采用的度分布［10］，其度分布函数如下

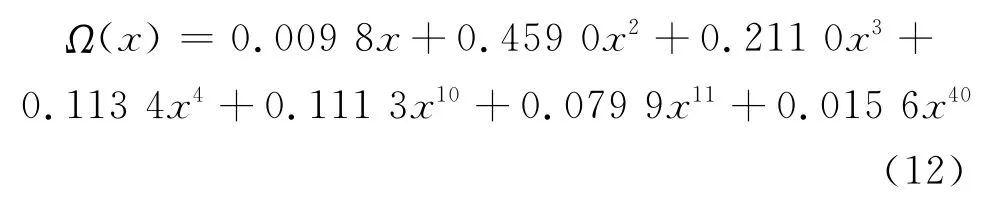
还有其他一些关于度分布优化方法的设计，比如用重要抽样法优化得到的短码长喷泉码的稀疏度分布函数［6］

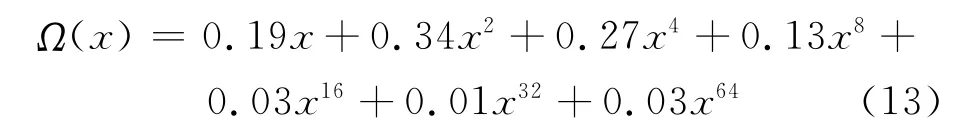
这两个度分布函数都是将Robust Soliton分布函数弱化，以在接收到K′＝k个编码分组时的译码成功率为目标函数，采用BP迭代译码算法，通过提高此时的译码成功率来优化得到的度分布。

2.2.2 短LT码度分布

针对短码长LT码，如果译码时采用BPGE译码算法，当经过删除信道后的生成矩阵H列满秩（rank（H）＝k）时，就可以成功译码。因此，优化度分布的目标即是满足rank（H）＝k的条件下尽可能降低所需接收编码分组数。文献［6］定义此优化目标函数为全部分组都译码成功时所需接收的平均编码分组数，记为MinAvg。

文献［2］在最初设计LT码时，得到度分布服从Ideal Soliton函数时LT码性能渐进最优，但实际应用中由于存在抽样误差，无法达到精准理论分布。其改进型Robust Soliton分布通过引入参数c和δ来调节性能，有较大实际应用价值。而削弱之后的度分布，如式（12）和（13），虽然降低了一定的编码复杂度，但对于码长较短的短LT码，其编码分组的度选择范围受到限制时，容易产生相同的编码分组，即引起短环，致使其成功译码时所需的MinAvg高于Robust Soliton分布。

因此，本方案采用优化参数后的Robust Soliton分布，并将在第3节仿真对比采用BPGE译码时各度分布的性能。

3 仿真分析

为了评估所提短LT码级联方案的性能，本节首先仿真对比了几类短码长LT码，验证相同接收包数下本文所提短LT码的译码成功率更高。然后对本文设计的级联方案在无线信道中的应用进行仿真，验证此级联方案的有效性，并给出了不同等效信道删除概率下的译码开销。

3.1 短LT码设计方法对比

本节构造了码长k＝100的短LT码，编码度分布服从参数为δ＝0.05，c＝0.03的 Robust Soliton函数，译码采用本文提出的BPGE算法。文献［6］中的短LT码采用式（13）度分布，译码采用BP算法。首先对这两种设计方案作性能对比。为了比较各类度分布的性能，在译码都采用BPGE算法时，本文也仿真了编码采用文献［6，10］中的度分布。

对以上4种设计方法分别进行104次蒙特卡洛仿真，每次仿真发送原始分组包数为k＝100，发送端按给定度分布持续产生并发送编码分组包，直至接收端正确译码，记录此时接收的分组包数。对记录结果进行统计，以成功译码时接收的分组包数为横轴，将包数对应的译码成功次数换算成占总实验数的比例作为纵轴，绘出柱状图如图2～5所示。

图2 本文方案：RS度分布，BPGE译码Fig.2 This Scheme：RS degree distribution，BPGE decoding

图3 式（13）度分布，BP译码Fig.3 Formula 13degree distribution，BP decoding

图4 式（13）度分布，BPGE译码Fig.4 Formula 13degree distribution，BPGE decoding

图5 式（12）度分布，BPGE译码Fig.5 Formula 12degree distribution，BP decoding

对比图3和图4可以看出，在采用相同度分布时，BP译码算法成功译码的分组数集中在115至135之间，在120处峰值比例为0.11；而BPGE译码算法成功译码的分组数集中在105至120之间，在110处到达峰值，峰值比例约为0.15。因此采用BPGE译码算法降低了译码成功所需接收的平均分组数MinAvg。

然后对比图2，4和5，本文设计方案的成功译码分组数集中在110以内，峰值比例为0.35；而按其他两类削弱的度分布编码时，译码都已采用BPGE算法时，但成功译码的分组数大多集中在100至120之间，峰值比例相对较低。因此在采用BPGE译码时，Robust Soliton度分布的 MinAvg最低，性能最优。

3.2 短LT码级联方案性能分析

在仿真中采用传统的RS－CC级联码构造等效删除信道，即RS（255，223）码与（7，1／2）卷积码级联，在二者之间加入交织编码，调制方式选用QPSK。接收端卷积码采用软判决Viterbi译码，RS译码检测出接收编码分组包有不可纠错误时删去此包，这样就可以把RS编码之前和RS译码之后的整个子系统等效为删除信道。不同的删除概率对应AWGN信道不同信噪比下的RS－CC码的不可纠错误概率。

仿真时，LT码的原始数据分组个数，数据分组长度为l＝1 784bit＝8×223bit，编码时选用δ＝0.05，c＝0.03的Robust Soliton度分布，设定每次仿真产生的编码分组个数为有限值K＝120，LT译码采用BPGE译码算法。仿真实验时信源产生的数据在同一指定的Eb／N0值上重复发送105次，求出平均译码成功概率。

经RS－CC编码后的误码率如图6所示，在Eb／N0为3dB左右时已达到10－5量级。因此，选取了Eb／N0在2～3.5dB这一区间测试级联LT码的性能。

图6同时给出了RS－CC码与LT码级联前后的误包率，其中，RS－CC码的误包率即是RS译码时的不可纠错误包概率，即等效删除信道的删除概率。从图中可以看出，在Eb／N0值大于2.5dB后，即等效信道的删除概率低于0.1之后，级联LT码的误包率迅速降低。当误包率在10－3附近时，级联短LT码后的编码增益约0.75dB。对于无码率的LT码，随着Eb／N0值的增加或等效包删除概率的降低，发送编码分组包的数量可适当降低。

图7显示了等效包删除概率p取0.01，0.1，0.2和0.4时，不同发送编码包数对应的成功译码概率，即在给定包删除概率条件下成功恢复的原始信息包数与k的比值。译码开销是在成功恢复出所有信息包时，发送端至少要发送的编码包个数K与k的差值除以k。从图7可以看出，在等效包删除概率为0.1时，接收端成功译码需要发送编码包个数为K＝126，因此译码开销为（K－k）／k＝0.26。当Eb／N0下降即等效包删除概率降低时，译码开销也迅速降低，如图当删除概率为0.01时，译码开销约为0.12。

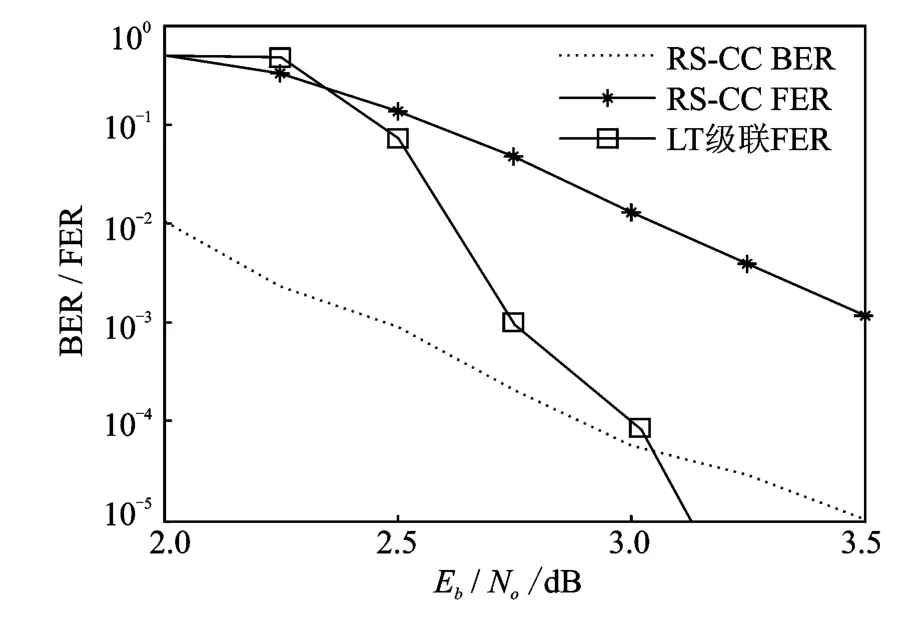
图6 LT码级联前后的误比特率与误包率Fig.6 BER and FER of LT concatenated coding

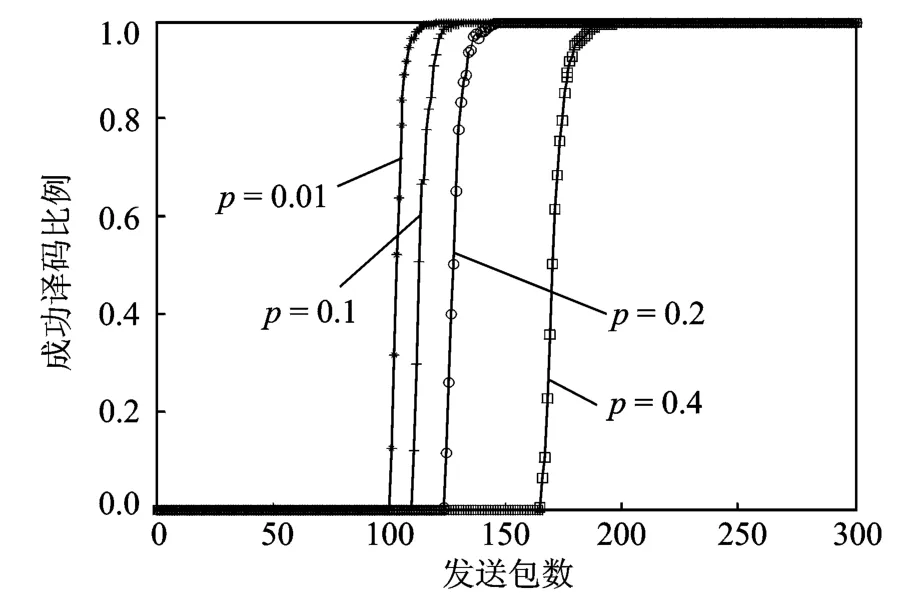
图7 发送编码包数与译码成功率Fig.7 Number of encoded frames and the success rate

4 结束语

该文通过分析喷泉码编译码算法与度分布的设计，提出了一种短LT码级联方案，方案利用RS－CC码的强纠错能力将无线信道构造为等效删除信道，再将文中设计的LT码与之级联，即可适应有实时通信要求的无线信道。仿真结果表明，此方案中的LT译码器只需正确接收略大于原始数据包数的编码包即可正确译码，当删除概率为0.01时译码开销约为0.12。并且信道Eb／N0大于2.5 dB后，该级联系统误包率较传统纠删码下降更迅速。但由于文中的LT码非系统码，在信噪比过低时系统性能反而恶化，因此短码长系统喷泉码是本文下一步的改进方向。

［1］Mackay D J.Fountain codes［J］.IEE Proceedings Communications，2005，152（6）：1062－1068.

［2］Luby M.LT codes［C］∥Proc 43rd Ann IEEE Symposium on Foundations of Computer Science，Vancouver.Canada：IEEE，2002：271－282.

［3］Shokrollahi A.Raptor codes［J］.IEEE Transactions on Information Theory，2006，52（6）：2551－2567.

［4］Lin Y，Wu C，Zhang Q，et al.Application of the concatenation of the concatenation of RS and LT codes in deep communications［C］∥Third IEEE International Conference on Space Mission Challenges for Information Technology （SMC－IT）.Pasadena：IEEE，2009：29－33.

［5］卞银兵，酆广增.一种低复杂度的短LDPC码级联译码算法［J］.数据采集与处理，2010，25（2）：250－254.Bian Yinbing，Feng Guangzeng.Novel concatenation decoding algorithm for short LDPC codes with lower complexities［J］.Journal of Data Acquisition and Processing，2010，25（2）：250－254.

［6］Hyytia E，Tirronen T，Virtamo J.Optimizing the degree distribution of LT codes with an importance sampling approach［C］∥Proceedings of the 6th International Workshop on Rare Event Simulation（RESIM 2006），Bamberg，Germany：Tinbergen Institute，2006：64－73.

［7］焦健，张钦宇，李安国.面向深空通信的喷泉编码技术［J］.宇航学报，2010，31（4）：1156－1161.Jiao Jian，Zhang Xinyu，Li Anguo.A method of concatenated fountain codes in deep space communication［J］.Journal of Astronautics，2010，31（4）：1156－1161.

［8］Kim S，Ko K，Chung S.Incremental Gaussian elimination decoding of raptor codes over BEC［J］.IEEE Communications Letters，2008，12：307－309.

［9］Shokrollahi A，Lassen S，Krap R.Systems and processes for decoding a chain reaction code through inactivation［P］.U.S Patent：7633413B2，2009－12－15.

［10］3rd Generation Partnership Project.3GPP－TS－26.364－V9.4.0，multi－media broadcast／multicast services（MBMS）protocols and codes（release 9）［S］.Valbonne，France：3GPP Organizational Partners，2010.

［11］Lu F，Chuan H F，Cai J，et al.LT codes decoding：design and analysis［C］∥The IEEE International Symposium on Information Theory.Seoul，Korea：IEEE，2009：2492－2496.

［12］林永照，吴成柯，刘薇.LT码和q－LDPC码级联方案在深空通信中的应用［J］.电子与信息学报，2010，32（8）：1898－1903.Lin Yongzhao，Wu Chengke，Liu Wei.Applications of the concatenation of q－LDPC and luby transform codes in deep communications［J］.Journal of Electronics ＆ Information Technology，2010，32（8）：1898－1903.