数字喷泉码及网络喷泉码的最新进展
徐大专 邵汉钦 张小飞 许生凯
(南京航空航天大学电子信息工程学院,南京,210016)
引 言
随着互联网与宽带移动通信技术的迅猛发展,大型软件、音视频文件和流媒体的网络数据流量爆发式增长,对通信网络的服务能力和质量提出了更高的要求。有限的网络带宽与迅速增长的网络数据流量之间的矛盾将长期存在,近年来出现的数字喷泉技术和网络编码技术为提高网络传输效率和可靠性开辟了新的途径[1-5]。
数字喷泉码[6-9]是针对大规模网络数据分发和可靠传输而提出的一种新的信道编码方法。与传统的分组码不同,数字喷泉码可以按照某种概率分布独立地产生任意数量的码字。接收端不必关心具体的编码分组及分组的顺序,只要接收到足够多的编码分组,就能实现正确的译码。因此,数字喷泉码的接收端不需要对传输的每个分组进行反馈确认,从而避免了网络组播情况下形成的“反馈风暴”问题,大幅度提高网络的传输效率。数字喷泉码还是大数据备份的理想选择,与传统的备份方法相比,只需很小的开销就能实现可靠备份,且能利用网络的空间资源实现分布式备份。数字喷泉码具有广阔的应用前景,目前已被DVB-H和3GPP TS 26.346等国际标准[10-11]采用,并且正在参与其他多项国际标准的制定。
网络编码[12-13]是另一种提高传输效率的有效方法。传统的网络路由机制认为,中间节点只需对传输的信息进行简单的存储和转发,而不需要进行任何处理。然而,传统算法均达不到网络组播传输的理论最大容量。网络编码彻底推翻了这一传统观点,网络的中间节点通过对接收分组进行信息处理,可以达到最大流传输的理论极限。网络编码还可以节省带宽资源,平衡链路负载,减少能量消耗。目前,网络编码已经成为网络信息理论领域最受瞩目的研究热点。
将数字喷泉码和网络编码相结合,研究网络环境中网络喷泉码的基本原理与性质,具有重要的理论意义和应用价值:(1)数字喷泉码是利用时间资源的信道编码方法,网络编码是根据网络状态信息利用空间资源的提高网络传输效率的方法,网络喷泉码可以更充分利用空时两维资源,逼近网络传输的理论极限。(2)数字喷泉码的特点适合于大规模网络信息的并发传输,网络喷泉码可以大幅度提高整个网络的吞吐量。(3)网络喷泉码的中继节点只需进行简单的网络编码处理,而不需要进行数字喷泉码的译码和编码转发,减小了系统的复杂性,提高了处理速度。(4)随着云计算技术的广泛应用,大数据备份技术已成为云计算时代的基础,网络喷泉码为提高大数据备份的效率和可靠性提供了一条新的途径。基于此,数字喷泉编码理论与网络编码理论相结合形成了明显的研究趋势,正逐步成为近年来的研究热点。
本文围绕数字喷泉码和网络喷泉码的基本原理和关键技术展开论述,以期推动网络喷泉码在大规模网络信息分发、并行下载、合作传输以及大数据备份等领域的研究和实际应用。首先对当前数字喷泉码及网络喷泉码的最新研究进展进行了介绍,系统地总结了当前同构网络喷泉码关键技术的研究成果;然后介绍了一种异构网络喷泉码,分析了其理论框架和优化设计模型;其次针对译码转发中继网络中存在的非理想协作问题,提出了用于放大转发的一种新的乘积型物理层中继网络编码模型,并建立了基于该模型的无线信道物理层网络喷泉码的理论框架和设计模型;最后指出了网络喷泉码研究中存在的一些关键问题,并对网络喷泉码理论及应用的发展趋势进行了展望。
1 数字喷泉码
1.1 LT码
Luby等人于1998年首次提出了数字喷泉码的概念,但并未给出实用的喷泉码设计方案[6]。直到2002年,Luby提出了第一种实用的数字喷泉码,称为LT(Luby transform)码[7]。LT码是一种真正意义上的随机编码,不仅具有实际应用价值,而且结构简单,编译码方法简单,复杂度相对较低,故常用于数字喷泉码的理论分析。LT码由数据分组长度k和度分布Ω(x)来描述,记为LT(k,Ω(x))。度分布是定义在整数集{1,2,…,k}上的概率分布(Ω1,Ω2,…,Ωk),其中Ωi表示一个码字由i个原始数据分组进行编码的概率。度分布可以表示成生成多项式的形式,即称为度分布函数。LT码的编码过程非常简单,按以下步骤进行:
(1)根据度分布随机选取一个整数d作为度;
(2)从k个原始数据分组中随机选取d个不同的分组;
(3)对选取的d个数据分组作比特异或,得到一个编码分组。
以上过程重复进行,可以源源不断地生成任意数量的编码分组。原始数据分组和编码分组的关系可以用图1所示的Tanner图来表示。上层的k个变量节点表示数据分组,底层的n个输出节点表示编码分组,连接变量节点和输出节点的边由度分布函数表征。Tanner图是理解数字喷泉码编码和译码算法的基础。
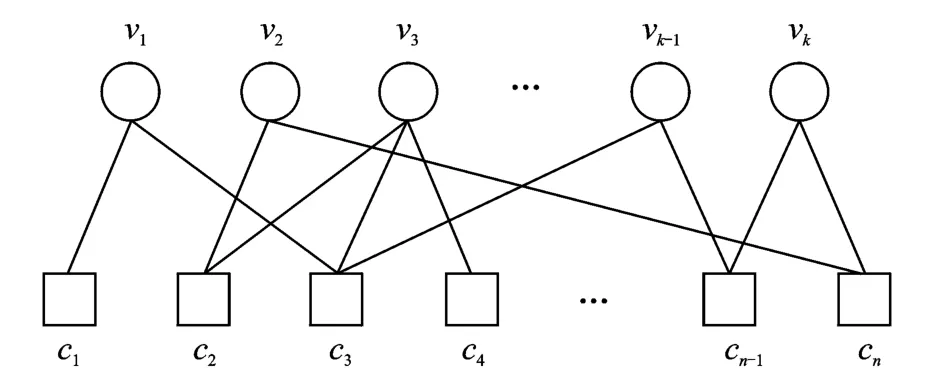
图1 LT码的Tanner图Fig.1 Tanner graph of a LT code
LT码的性能与译码方法密切相关[9],现有的译码方法分为置信传播(Belief propagation,BP)译码和高斯删除(Gaussian elimination,GE)译码两类。BP译码是一种低复杂度的迭代译码方法,译码过程如下[7]:
(1)任意选取一个度为1的编码分组。若不存在这样的编码分组,则译码结束;若存在,则通过复制可恢复与该编码分组相邻的唯一数据分组。
(2)根据Tanner图,将已恢复的数据分组的信息与相邻的所有其他编码分组进行模二和运算,更新编码分组的信息,并相应的将Tanner图中对应的边删除。
(3)重复以上步骤,直至找不到度为1的编码分组而结束译码。
GE译码是一种最大似然译码方法,虽然具有最好的误码率性能,但译码复杂度高,只适用于短码长喷泉码。Saejoon等[14]和 Bioglio等[15]分别改进了GE译码方法,分别提出了增量高斯删除译码方法和运行中高斯删除译码方法,对减小译码复杂度和时延有一定改善。朱宏鹏等[16]和朱宏杰等[17]则从混合译码的角度出发,将BP译码和GE译码或最大似然译码相结合,先进行BP译码,如果译码失败再对残留Tanner图进行GE译码或最大似然译码,减小了平均译码代价,提高了译码效率。
LT码的性能由其度分布决定,因此度分布的设计对LT码十分重要。常见的度分布为鲁棒孤波分布[7](Robust soliton distribution,RSD),定义如下
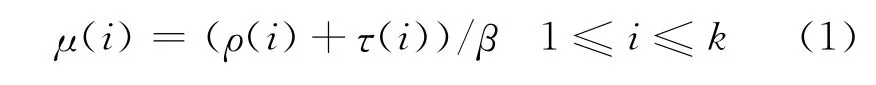

式中:R和δ为常数,且R≥1,δ∈[0,1]。RSD的性能较好,但仍不是最优的。朱宏鹏等[18]指出了LT码的最优度分布在实际应用中存在的问题,提出了一种实用的次优度分布。Zhu等[19]和焦健等[20]则致力于短码长LT码的度分布设计。
针对LT码的渐近性能分析,Luby等[21]提出了“与或树”分析方法。采用BP译码时,经过l次迭代,LT(k,Ω(x))码变量节点未正确恢复的概率为
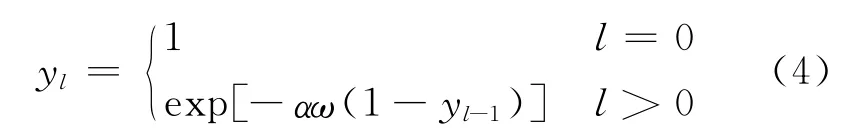
式中:α为平均输入度数,ω(x)=Ω′(x)/Ω′(1)为输出边分布。式(4)也称为密度演化方程,是喷泉码渐近译码性能分析的有力工具[21]。针对LT码的有限长分析,Karp等[22]提出了一种计算有限长LT码BP译码错误概率的方法,但复杂度较高。
1.2 Raptor码
LT码虽然编译码简单,但译码错误概率存在较高的平底效应,且编译码复杂度与分组长度呈非线性关系,因此不适用于长码。为此,Shokrollahi[8]提出了另一种改进的喷泉码,称为Raptor码。Raptor码是一种级联码,一般使用高码率的低密度奇偶校验(Low density parity check,LDPC)码或汉明码作为外码或预编码,以平均度数较小的弱LT码作为内码,其编码过程如图2所示。Raptor码的译码相应的也分为两步,首先采用BP译码恢复出中间符号,再利用传统的纠错码译码方法对中间符号进行译码。由于预编码具有一定的纠错能力,放松了对LT编码的要求,因此整体编译码复杂度降低为线性复杂度,并且克服了LT码的错误平底效应,在误码率和代价两方面都达到优越的性能。
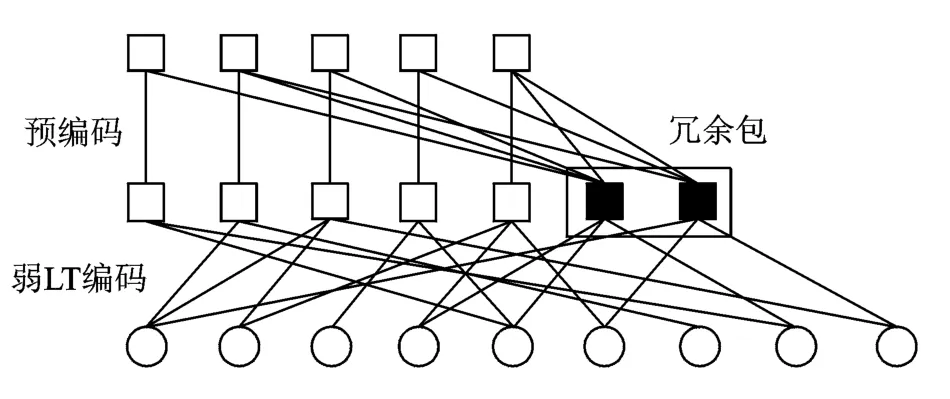
图2 Raptor码编码过程Fig.2 Encoding process of a Raptor code
1.3 不等保护喷泉码
针对实际应用中不同信息在重要性和交付时间程度方面的差异,需要设计不等错误保护(Unequal error protection,UEP)能力或不等恢复时间(Unequal recovery time,URT)喷泉码。Rahnavard等通过为不同类信息分配不同的概率权重,提出了一种加权LT(Weighed LT,WLT)码[23],可提供不等错误保护能力。Sejdinovic等对不同类信息分层,提出了一种扩展窗喷泉码(Expanding window fountain,EWF)[24],这种方法为喷泉码的设计带来更大的灵活性,所设计的EWF码具有 UEP/URT特性。Vukobratovic等[25]和Na-zir等[26]分别将EWF码应用于视频多播传输和H.264视频传输,获得了良好的性能。Talari等[27]提出了一种针对两源单中继网络的分布式UEP喷泉码,通过为两个源分配不同的分组长度来实现UEP能力。Arslan等[28]得到了一种广义的LT码,具有比WLT码和EWF码更好的性能。Ni等[29]提出了一种具有UEP特性的复制扩展窗喷泉码,将虚拟扩展技术引入到EWF码中。
1.4 无线信道数字喷泉码
数字喷泉码最初是针对二进制删除信道提出的一种前向纠删码。将数字喷泉码作为加性高斯白噪声(Additive white Gaussian noise,AWGN)信道或衰落信道的信道编码是最近的研究热点。早在2004年,Palanki和 Yedidia[30]指出LT码在噪声信道中存在明显的“差错平台”现象,而Raptor码则不存在明显的差错平台。Etesami和Shokrollahi[31]证明了删除信道中好的LT码和Raptor码在AWGN信道中仍具有较好的性能,并采用EXIT图方法对LT码进行了优化。Niesen等[32]研究了高斯多址接入信道下的喷泉码性能,提出了一种喷泉多址接入方案。Castura和Mao[33]提出了一种在衰落信道下进行喷泉编码传输的方案,当接收端未知信道状态信息时,该方案比传统的固定码率编码方案具有更好的性能。Venkiah等[34]分析了Raptor码的渐近性能,并对Raptor码的度分布进行了优化设计。Erez等[35]设计了一种无率码编译码方案,能够逼近AWGN信道的容量,且具有较低的译码复杂度。Bai等[36]提出了一种适用于AWGN信道和衰落信道的无速率码,能够有效地降低“差错平台”。Chen等[37]提出了一种适用于AWGN信道的非级联形式的喷泉AR码,解决了LT码在AWGN信道下的“差错平台”问题。
2 同构网络喷泉码
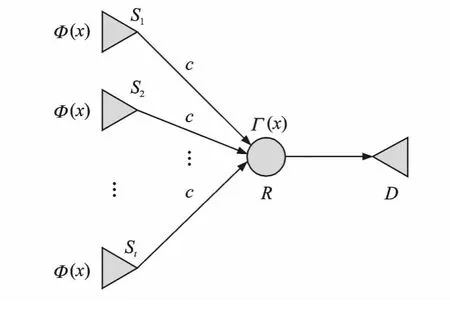
图3 同构网络模型Fig.3 Homogeneous network model
数字喷泉码与网络编码的融合是近几年涌现出的新的研究方向,两者的结合能够进一步提高网络的传输效率。本文将数字喷泉码和网络编码的有机结合称为网络喷泉码,并将各信源具有相同度分布或相同接入信道容量的多信源接入网络称为同构网络,如图3所示,相应的喷泉编码方案称为同构网络喷泉码。Puducheri等[38]针对同构网络提出了一种分布式LT(Distributed LT,DLT)编码方案,利用网络编码的思想,中继节点对多源输入分组进行异或转发。Sejdinovic等[39]将DLT码推广到任意个信源的情况,提出了选择分布式LT(Selective distributed LT,SDLT)码,但其研究仅限于同构信源,未涉及多个信源具有不同度分布的情况。2010年,他们用类似的分析和设计方法研究了一类非中心化的分布式LT码[40],能够适用于不同的场景,并且具有UEP能力。Liau等[41]针对两信源单中继的Y型网络提出了一种类孤波分布的喷泉编码(Soliton-like rateless coding,SLRC)方案,使得总体度分布能够接近孤波分布,从而可以采用BP译码算法进行高效译码,其性能优于DLT码和SDLT码。在2013年,他们在中继资源受限的情况下进一步改进了中继的再编码算法,降低了SLRC的复杂度[42]。
除了多信源接入网络外,不少学者对多跳线型中继网络[43-46]和协作中继网络[47-50]等网络模型中的网络喷泉码进行了研究。
3 异构网络喷泉码
针对多信源接入网络,目前大多数研究工作只限于同构信源同构信道的情况,而对异构信源异构信道的网络喷泉码问题则很少涉及。基于此,作者提出了一种异构网络喷泉码,将数字喷泉码从同构网络推广到了一般的异构网络环境[51],研究了其网络模型和网络编码策略,以及度分布描述方法和性能分析方法,并从设计上研究其优化设计模型及优化方法。
图4所示为含有t个信源、单个中继和单个目标节点的异构网络的一般模型。该模型中,Φi(xi)表示信源Si的度分布函数,Γ(x)表示中继进行喷泉编码的度分布,ci表示信源Si与中继之间接入信道的信道容量。
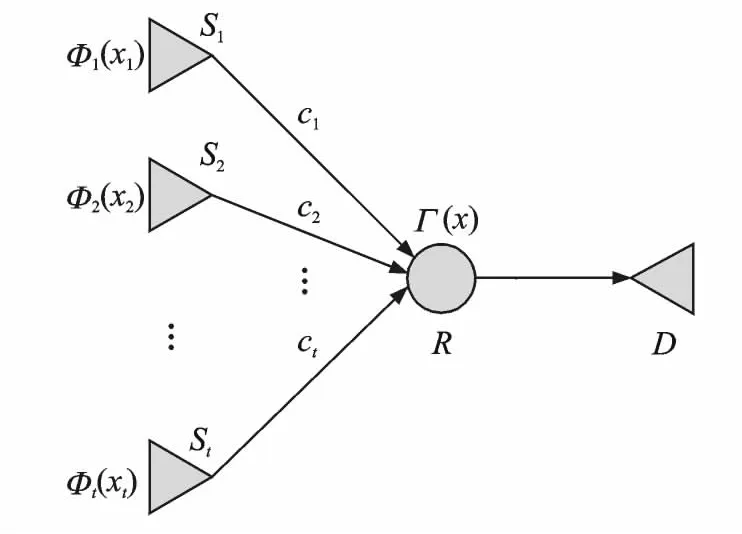
图4 异构网络模型Fig.4 Heterogeneous network model
在同步和异步的情况下,网络编码采取不同的策略。同步编码策略采用编码转发,异步编码策略要考虑接入信道容量差异和缓冲器的设计,以一定的概率进行编码转发和选择性转发。两种编码策略都改变了信源的度分布,需要将信源、中继和信道容量作为整体进行联合设计。
异构网络中不同信源的译码错误概率是不同的,该网络喷泉码的度分布函数不能用传统的一元度分布函数表示。为此,作者提出了多元度分布函数的概念[51],异构网络的多元输出度分布函数为
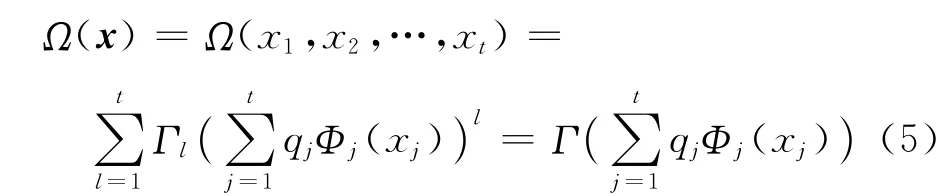
式中:qi为信源Si接入中继的概率,与信源Si接入信道的信道容量有关,可按qi=ci/c计算,且c=当各信源的输出度分布和接入信道容量相同时,输出度分布为一元函数Ω(x)=Γ(Φ(x)),即退化为同构信源的情况。
在同构信源同构信道的情况下,边的输出度分布用节点输出度分布的导数来定义,而在异构信源或者异构信道的情况下,不同信源边的输出度分布将由多元度分布函数的一组偏导数来定义[51]。图4所示异构网络的边的输出度分布函数为
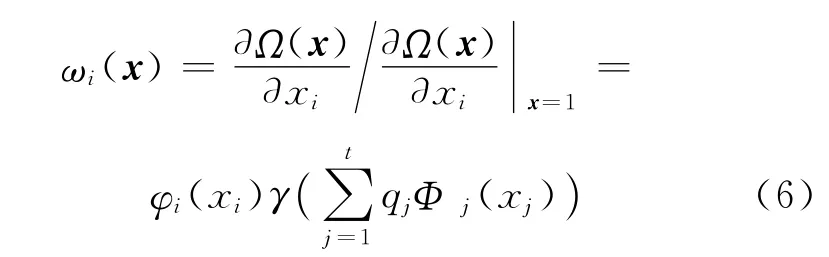
式中:φi(xi)=Φ′i(xi)/Φ′i(1)为各信源的边分布函数,γ(x)=Γ′(x)/Γ′(1)为中继的边分布函数。
在以上分析的基础上,可得多元密度演化方程组如下[51]
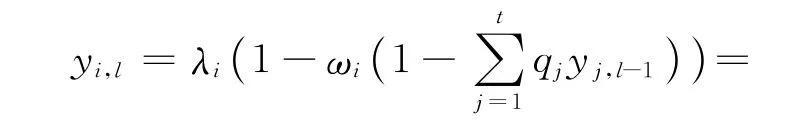
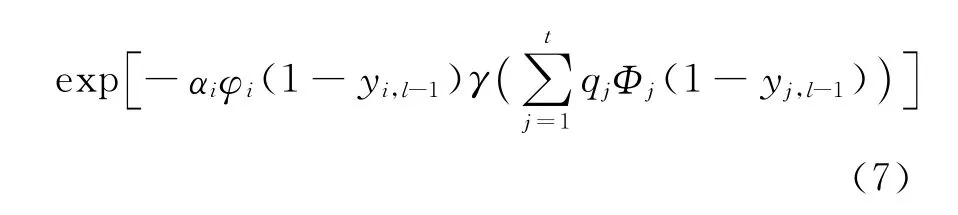
式中:αi为信源的平均输入度,下标l表示迭代的次数。当l趋于无穷大时,式(7)即为BP算法的渐近译码失败概率,可以用来分析异构网络喷泉码的渐近性能。此外,密度演化方程还是网络喷泉码优化设计的基础。以密度演化方程为主要约束条件,以最小开销或最小复杂度为优化目标,可以得到最优准则下的度分布优化设计模型。
4 无线网络喷泉码
在无线网络中,由于存在噪声的干扰,中继节点直接采用异或编码会使得网络喷泉码的总体度分布较为复杂,难以对其性能进行分析,因此目前大多采用译码转发的方案。Zhang等[52]针对两信源单中继网络,提出了一种基于喷泉码的联合信道编码和网络编码的方案,设计了一种适用于中继节点的二维LT编码方法,并对信源和中继进行联合设计,所提方案的性能优于传统的联合信道编码和网络编码方案。此外,Zhang等[53]还针对三时隙双向中继网络,提出了一种基于译码转发的联合信道编码和网络编码的方案,并在AWGN信道和Rayleigh衰落信道下进行了优化设计,取得了较好的性能。
译码转发无线中继网络中,网络编码以中继节点完全正确译码为前提,当中继存在译码错误时,存在非理想协作问题。为此,本文提出了一种乘积型物理层网络编码模型,可避免中继节点在译码转发时产生的误码扩散问题。该模型采用放大转发方式,避免了非理想协作问题,并大幅度减小了中继节点处理的复杂度。据此,本文提出了无线网络喷泉码的概念,并给出了关于无线网络喷泉码理论分析框架和设计模型的初步设想。
常见的无线网络模型如图5和图6所示。图5为分布式中继网络模型,信源S1和S2分别在时隙1和时隙2向中继R发送数据包,中继R对接收到的数据包进行编码后在时隙3发送数据包给目标节点D。图6为多信源/多目标协作中继网络模型,信源S1在时隙1向中继和目标D1发送数据包,信源S2在时隙2向中继和目标D2发送数据包,中继对接收到的数据包进行编码后在时隙3发送数据包给目标D1和D2。此外,双向中继网络和多跳中继网络等也是研究的基本网络模型。
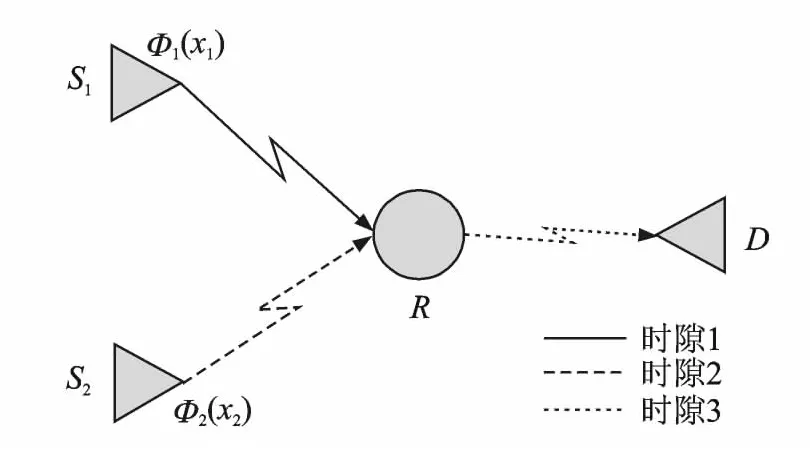
图5 分布式中继网络模型Fig.5 Distributed relay network model

图6 多信源/多目标协作中继网络模型Fig.6 Multi-source/multi-object cooperative relay network model
在乘积型物理层网络编码模型中,中继节点将时隙1和时隙2收到的模拟信号直接相乘,并放大转发,从而避免了译码转发网络编码存在的非理想协作问题。乘积型物理层网络编码方法的特点是将模拟域“乘法”运算等价于比特域的“异或”运算,如图7所示。
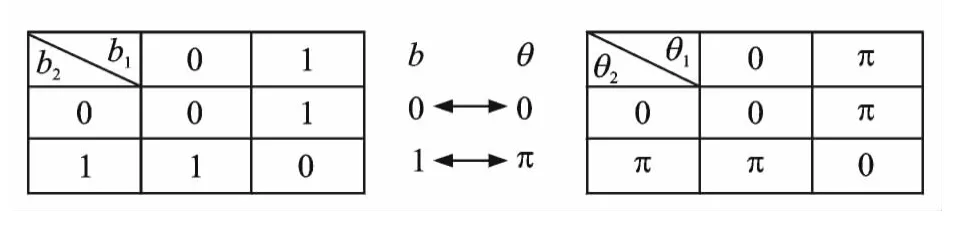
图7 BPSK调制系统中,模拟域“乘法”运算与比特域“异或”运算的等价关系Fig.7 Equivalent relationship between multiplication(on analog domain)and exclusive-or (on bit domain)in BPSK modulation systems
乘积型物理层网络编码模型的性能与普通模型相当。仿真结果表明,在AWGN信道上,乘积模型优于普通模型,而在Rayleigh信道上,普通模型优于乘积模型,相差都在1dB以内。
根据图7所示的等价关系,可得经过中继节点乘积编码后,无线网络喷泉码的总体度分布为
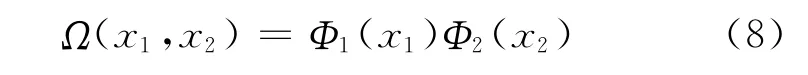
无线网络喷泉码的译码可以采用传统纠错码的译码方法,如BP迭代译码。令mloi为第l次译码迭代时输出节点o传递给输入节点i的对数似然比信息,为第l次译码迭代时输入节点i传递给输出节点o的对数似然比信息,Zo为每个输出节点对应的初始对数似然比信息,则第l次迭代时输出节点的信息更新公式为
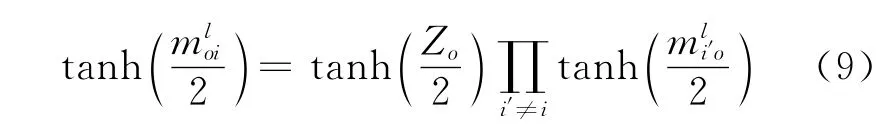
输入节点的信息更新公式为
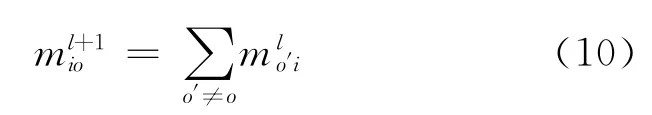
式中:l=0时的初值为=0,tanh(·)表示正切函数。
无线网络喷泉码的渐近性能分析可以采用与传统纠错码类似的密度演化分析方法,如高斯近似方法和EXIT图分析方法等。高斯近似假设每次迭代的传递信息都服从高斯分布,这与度数较大的输入节点较为吻合,而对度数较小的输出节点不成立。EXIT图分析方法用互信息表示外部信息转移函数,精度更高。令μl为第l次迭代时输入节点传递给输出节点的信息的均值,定义fd(μl)为

式中:Xi是均值为μl的相互独立的对称高斯变量,Z是信道的对数似然比信息,atanh(·)表示反正切函数,E[·]表示期望。因此,第l+1次迭代时输入节点传递给输出节点的信息的均值为
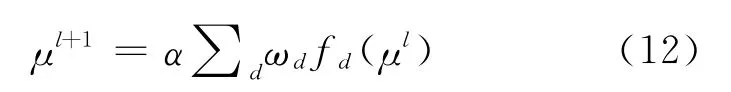
式中:ω(x)=∑dωdxd-1为输出节点的边度分布,α为平均输入度。式(12)就是基于EXIT图的密度演化方程,可用于分析无线网络喷泉码的渐近性能。
与异构网络喷泉码类似,EXIT图分析方法可以用于无线网络喷泉码的优化设计,同样可以最小开销或最小复杂度为目标函数构造优化模型。以最小复杂度优化模型为例,根据式(12)可以得到如下约束优化方程
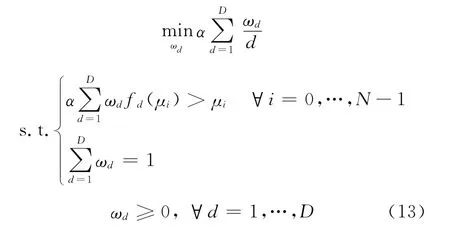
式(13)可以采用线性规划方法来求解。
5 结束语
从1998年Luby等提出数字喷泉编码的概念以来,数字喷泉码的研究已经取得了丰富的成果。网络喷泉码是数字喷泉码在网络环境中的自然扩展,也是当前数字喷泉码研究的一个重要趋势,正引起越来越多的关注。如何从网络整体考虑,研究网络编码策略和网络喷泉码的度分布问题,使网络吞吐量最大化是网络喷泉码面临的挑战。目前对于网络喷泉码的研究仍处于起步阶段,现有的成果仍是零散和局部的,系统性的理论分析框架和设计方法尚未形成,仍存在着许多重要的理论和技术问题亟待解决:
(1)目前的研究工作主要针对基本的网络模型如多跳中继网络、多信源接入网络和双向中继网络等展开,而对于一般的复杂网络模型中的网络喷泉码的编译码机制和性能分析,现有的研究工作非常有限,需要进一步的深入研究,以推动网络喷泉码在一般网络中的应用;
(2)目前对于无线网络喷泉码的研究主要基于译码转发异或型网络编码模型,而对放大转发异或型网络编码模型研究的较少。该模型中,总体度分布与各信源度分布的关系较为复杂,如何分析其渐近性能,并与已有方案进行比较,仍是有待解决的问题。对该问题的研究可以丰富无线网络编码理论。
(3)本文提出的乘积型物理层网络编码模型可以解决译码转发网络编码存在的非理想协作问题,但目前只适用于低阶PSK调制系统。对于高阶调制系统,模拟域的乘法运算与比特域的异或运算之间的对应关系仍有待进一步考察,乘积型物理层网络编码的性能还有待进一步研究;
网络喷泉码作为数字喷泉码的重要分支,是一项新兴的高效网络传输技术,目前正处于不断发展和完善的阶段。随着网络喷泉码理论和应用研究的不断深入和完善,研究成果必将丰富和发展网络信息理论,促进网络喷泉码在大规模数据传输和云数据备份领域的应用。
[1]Mitzenmacher M.Digital fountains:a survey and look forward[C]//2004IEEE Information Theory Workshop.San Antonio.USA:IEEE,2004:271-276.
[2]慕建君,焦晓鹏,曹训志.数字喷泉码及其应用的研究进展与展望[J].电子学报,2009,37(7):1571-1577.Mu Jianjun,Jiao Xiaopeng,Cao Xunzhi.A survey of digital fountain codes and its application[J].Acta Electronica Sinica,2009,37(7):1571-1577.
[3]Bassoli R,Marques H,Rodriguez J,et al.Network coding theory:a survey[J].IEEE Communications Surveys & Tutorials,2013,15(4):1950-1978.
[4]Matsuda T,Noguchi T,Takine T.Survey of network coding and its applications[J].IEICE Transactions on Communications,2011,E94-B(3):698-717.
[5]Liew S C,Zhang S,Lu L.Physical-layer network coding:Tutorial,survey,and beyond[J].Physical Communication,2013,6:4-42.
[6]Byers J W,Luby M,Mitzenmacher M,et al.A digital fountain approach to reliable distribution of bulk data[J].ACM Sigcomm Computer Communication Review,1998,28(4):56-67.
[7]Luby M.LT codes[C]//Proc 2002IEEE Symp Foundations of Computer Science(FOCS).Vancouver.Canada:IEEE,2002:271-280.
[8]Shokrollahi A.Raptor codes[J].IEEE Transactions on Information Theory,2006,52(6):2551-2567.
[9]Mackay D J C.Fountain codes[J].IEE Proceedings-Communications,2005,152(6):1062-1068.
[10]3rd Generation Partnership Project.Technical specification group services and system aspects;multimedia broadcast/multicast services(MBMS);protocols and codecs(Release 11)[S].3GPP TS 26.346V11.2.0-2012,Volbonne,France:3GPP,2012.
[11]石东新,杨占昕,张铨.3GPP MBMS中Raptor编解码研究[J].数据采集与处理,2010,25(S1):120-124.Shi Dongxin,Yang Zhanxin,Zhang Quan.Key technologies and performance analysis of raptor codes in 3GPP MBMS[J].Journal of Data Acquisition and Processing,2010,25(S1):120-124.
[12]Ahlswede R,Ning C,Li S Y R,et al.Network information flow[J].IEEE Transactions on Information Theory,2000,46(4):1204-1216.
[13]Li S Y R,Yeung R W,Ning C.Linear network coding[J].IEEE Transactions on Information Theory,2003,49(2):371-381.
[14]Saejoon K,Karam K,Sae-Young C.Incremental Gaussian elimination decoding of raptor codes over BEC[J].IEEE Communications Letters,2008,12(4):307-309.
[15]Bioglio V,Grangetto M,Gaeta R,et al.On the fly Gaussian elimination for LT codes[J].IEEE Communications Letters,2009,13(12):953-955.
[16]朱宏鹏,李广侠,冯少栋.LT码的BPML译码算法[J].计算机科学,2009,36(10):77-81.Zhu Hongpeng, Li Guangxia,Feng Shaodong.BPML decoding algorithm of LT codes[J].Computer Science,2009,36(10):77-81.
[17]朱宏杰,裴玉奎,陆建华.一种提高喷泉码译码成功率的算法[J].清华大学学报:自然科学版,2010,50(4):609-612.Zhu Hongji,Pei Yukui,Lu Jianhua.Algorithm improving the decoding performance of fountain codes[J].Journal of Tsinghua University:Science and Technology,2010,50(4):609-612.
[18]朱宏鹏,张更新,李广侠.卫星数据广播分发系统中LT码的研究[J].通信学报,2010,31(7):122-127.Zhu Hongpeng,Zhang Gengxin,Li Guangxia.Research of LT code in satellite data broadcasting system[J].Journal on Communications,2010,31(7):122-127.
[19]Zhu H,Zhang C,Lu J.Designing of fountain codes with short code-length[C]//The Third International Workshop on Signal Design and Its Applications in Communications(IWSDA 2007).Chengdu,China:IEEE,2007:65-68.
[20]焦健,杨志华,顾术实,等.基于随机置换展开与停止集的LT码联合编译码算法[J].通信学报,2013,34(2):31-39.Jiao Jian,Yang Zhihua,Gu Shushi,et al.Novel joint encoding/decoding algorithms of LT codes based on random permute egde-growth and stopping set[J].Journal on Communications,2013,34(2):31-39.
[21]Luby M G,Mitzenmacher M,Shokrollahi M A.A-nalysis of random processes via And-Or tree evaluation[C]//Proceedings of the Ninth Annual ACM-SIAM Symposium on Discrete Algorithms.San Francisco,USA:Society for Industrial and Applied Mathematics,1998:364-373.
[22]Karp R,Luby M,Shokrollahi A.Finite length analysis of LT codes[C]//2004IEEE International Symposium on Information Theory (ISIT).Chicago,USA:IEEE,2004:39.
[23]Rahnavard N,Vellambi B N,Fekri F.Rateless codes with unequal error protection property[J].IEEE Transactions on Information Theory,2007,53(4):1521-1532.
[24]Sejdinovic D,Vukobratovic D,Doufexi A,et al.Expanding window fountain codes for unequal error protection[J].IEEE Transactions on Communications,2009,57(9):2510-2516.
[25]Vukobratovic D,Stankovic V,Sejdinovic D,et al.Scalable video multicast using expanding window fountain codes[J].IEEE Transactions on Multimedia,2009,11(6):1094-1104.
[26]Nazir S,Stankovic V,Vukobratovic D.Expanding window random linear codes for data partitioned H.264video transmission over DVB-H network[C]//2011 18th IEEE International Conference on Image Processing(ICIP).Brussels,Belguim:IEEE,2011:2205-2208.
[27]Talari A,Rahnavard N.Distributed unequal error protection rateless codes over erasure channels:a two-source scenario[J].IEEE Transactions on Communications,2012(99):1-7.
[28]Arslan S S,Cosman P C,Milstein L B.Generalized unequal error protection LT codes for progressive data transmission[J].IEEE Transactions on Image Processing,2012,21(8):3586-3597.
[29]Ni C,Hou C,Xiang W.A novel UEP scheme based upon rateless codes[C]//2012IEEE Wireless Communications and Networking Conference(WCNC).Shanghai,China:IEEE,2012:592-596.
[30]Palanki R,Yedidia J S.Rateless codes on noisy channels[C]//2004IEEE International Symposium on Information Theory (ISIT).Chicago,USA:IEEE,2004:37.
[31]Etesami O,Shokrollahi A.Raptor codes on binary memoryless symmetric channels[J].IEEE Transactions on Information Theory,2006,52(5):2033-2051.
[32]Niesen U,Erez U,Shah D,et al.Rateless codes for the Gaussian multiple access channel[C]//2006IEEE Global Telecommunications Conference (GLOBECOM).San Francisco,USA:IEEE,2006:1-5.
[33]Castura J,Mao Y.Rateless coding over fading channels[J].IEEE Communications Letters,2006,10(1):46-48.
[34]Venkiah A,Poulliat C,Declercq D.Jointly decoded raptor codes:Analysis and design for the BIAWGN channel[J].Eurasip Journal on Wireless Communications and Networking,2009,10:1155.
[35]Erez U,Trott M D,Wornell G W.Rateless coding for Gaussian channels[J].IEEE Transactions on Information Theory,2012,58(2):530-547.
[36]Bai B,Bai B,Ma X.Simple rateless error-correcting codes for fading channels[J].Science China Information Sciences,2012,55(10):2194-2206.
[37]Chen S,Zhang Z,Zhu L,et al.Accumulate rateless codes and their performances over additive white gaussian noise channel[J].IET Communications,2013,7(4):372-381.
[38]Puducheri S,Kliewer J,Fuja T E.The design and performance of distributed LT Codes[J].IEEE Transactions on Information Theory,2007,53(10):3740-3754.
[39]Sejdinovic D,Piechocki R J,Doufexi A.AND-OR tree analysis of distributed LT codes[C]//Proceedings 2009IEEE Information Theory Workshop on Networking and Information Theory.Volos,Greece:IEEE,2009:261-265.
[40]Sejdinovic D,Piechocki R,Doufexi A,et al.Decentralised distributed fountain coding:asymptotic analysis and design[J].IEEE Communications Letters,2010,14(1):42-44.
[41]Liau A,Yousefi S,Il-Min K.Binary soliton-like rateless coding for the Y-Network[J].IEEE Transactions on Communications,2011,59(12):3217-3222.
[42]Liau A,Kim I,Yousefi S.Improved low-complexity soliton-like network coding for a resource-limited relay[J].IEEE Transactions on Communications,2013,61(8):3327-3335.
[43]Gummadi R,Sreenivas R S.Relaying a fountain code across multiple nodes[C]//2008IEEE Information Theory Workshop (ITW 2008).Porto,Portugal:IEEE,2008:149-153.
[44]Champel M L,Huguenin K,Kermarrec A M,et al.LT network codes[C]//2010International Conference on Distributed Computing Systems(ICDCS 2010).Genova,Italy:IEEE,2010:536-546.
[45]Apavatjrut A,Goursaud C,Jaffres-Runser K,et al.Toward increasing packet diversity for relaying LT fountain codes in wireless sensor networks[J].IEEE Communications Letters,2011,15(1):52-54.
[46]Lv S,Zhao Z,Zhang H.LT coding over the network[C]//2010International Conference on Wireless Communications and Signal Processing (WCSP).Suzhou,China:IEEE,2010:1-5.
[47]Castura J,Mao Y.Rateless coding for wireless relay channels[J].IEEE Transactions on Wireless Communications,2007,6(5):1638-1642.
[48]Gong C,Yue G,Wang X.Analysis and optimization of a rateless coded joint relay system[J].IEEE Transactions on Wireless Communications,2010,9(3):1175-1185.
[49]Lei W,Xie X,Li G.Performance analysis of wireless dynamic cooperative relay networks using fountain codes[J].Journal of Communications,2010,5(4):307-316.
[50]雷维嘉,谢显中,李广军.采用数字喷泉码的无线协作中继方案及其性能分析[J].电子学报,2010,38(1):228-233.Lei Weijia, Xie Xianzhong,Li Guangjun. The scheme and performance of wireless cooperative relay system using digital fountain codes[J].Acta Electronica Sinica,2010,38(1):228-233.
[51]Shao H,Xu D,Zhang X.Asymptotic analysis and optimization for generalized distributed fountain codes[J].IEEE Communications Letters,2013,17(5):988-991.
[52]Zhang Y,Zhang Z.Joint network-channel coding with rateless code over multiple access relay system[J].IEEE Transactions on Wireless Communications,2013,12(1):320-332.
[53]Zhang Y,Zhang Z,Yin R,et al.Joint networkchannel coding with rateless code in two-way relay systems[J].IEEE Transactions on Wireless Communications,2013,12(7):3158-3169.
——以鲁甸地震相关新浪微博为例

