宽线性波束形成技术综述
叶中付 徐东阳 曹圣红 徐 旭
(1.中国科学技术大学信息科学技术学院,合肥,230027;2.中国科学技术大学语音及语言信息处理国家工程实验室,合肥,230027)
引 言
线性滤波理论是信号处理的主要研究内容之一,它广泛应用于通信、雷达、声纳、射电天文、地震勘探等领域。
早期人们通常认为信号是圆的、平稳的,对于由期望信号s(t)、干扰m(t)和噪声v(t)叠加产生的观测信号x(t),线性滤波的目标是使期望信号s(t)最佳接收。线性滤波最基本的输出形式是y(t)≜wHx(t),w是时不变的权重矢量,x(t)是观测矢量[1]。当观测矢量x(t)是时间序列时,称为时域线性滤波,例如基于最小均方误差准则的维纳滤波[2]。当观测矢量x(t)是多天线数据时,称为空域线性滤波或波束形成,例如最小方差无畸变响应 (Minimum variance distortionless response,MVDR)波束形成[3]。
随着人们对信号统计特性认识的加深,发现在通信领域有些人工调制信号是非圆的,例如BPSK、AM、PAM、MASK 和 UQPSK[4]。非圆信号不仅存在协方差矩阵,还存在伪协方差矩阵(又称补协方差或共轭协方差矩阵)。为了同时利用这两个矩阵,滤波器的输出形式变为y(t)≜w1(t)H·x(t)+w2(t)Hx(t)*,其中w1(t)和w2(t)是时变的权重矢量,这种形式的滤波称为宽线性滤波[5-6]。当观测矢量x(t)是时间序列时,称为时域宽线性滤波,通常假设期望信号波形已知或存在训练数据,利用这些先验知识,很容易实现各种类型的时域宽线性滤波算法[7-15]。当观测矢量x(t)是多天线数据时,称为宽线性波束形成[16-20]。
最早提出的时不变宽线性波束形成算法假设干扰是非圆的,通过抑制非圆干扰来降低输出信号中干扰的影响[16]。这种宽线性波束形成算法仅仅考虑了干扰的非圆特性,没有考虑期望信号的非圆特性,因此性能还没有达到最优。为了利用期望信号的非圆特性,文献[17]提出了最优宽线性波束形成算法。该算法通过将期望信号的共轭分量正交分解为与期望信号相关的分量及其正交分量,获得了一个扩展的导向矢量,然后应用于传统的波束形成技术,提出了宽线性MVDR波束形成器。该算法大大提升了宽线性波束形成算法的性能上限,并能抑制多于阵元数的干扰。实现该算法的前提是已知期望信号的非圆系数或有训练序列用于估计扩展的导向矢量。然而在频谱感知和被动监听领域中这些条件很难满足,因此需要对期望信号的非圆系数进行估计。
文献[18]提出了一种非圆系数的估计算法,首先通过最大化波束输出功率得到非圆系数的初始估计,然后分析噪声的影响,对初始的非圆系数估计进行修正。考虑到非圆系数的估计误差会导致扩展的导向矢量失配,可以利用对角加载技术来减小估计误差对宽线性波束形成器性能的影响。另外,针对基带信号存在偏移频率的情况,文献[18]还提出了一种频移宽线性波束形成算法,该算法利用共轭循环相关系数代替非圆系数进行宽线性波束形成,当偏移频率不为零时,该算法优于最优宽线性波束形成算法。
在实际应用中,期望信号的名义导向矢量与真实导向矢量可能失配,这会导致波束形成器的性能急剧下降,因此需要研究稳健的宽线性波束形成算法。文献[20]提出了两种基于不确定集的稳健宽线性波束形成算法,算法中假设非圆系数误差和导向矢量误差是不相关的,通过约束这两类误差上限来进行稳健的宽线性波束形成。
1 信号模型和线性波束形成
1.1 圆信号与非圆信号
实际通信系统中,信号下变频到基带后,由同相分量和正交分量可得复信号,根据其统计特性的不同分为圆信号和非圆信号。信号的统计特性包含概率密度函数、矩函数及累积量等。由于波束形成中利用的是数据的矩,所有的宽线性波束形成均将圆特性和非圆特性定义为矩圆特性和矩非圆特性。所谓矩圆特性和矩非圆特性是指,信号乘以一个相位因子ejφ后,即绕圆心旋转,其二阶矩相对于不旋转的信号的变化情况。“圆”是指绕圆心旋转不变,“非圆”的含义相反。简言之,二阶矩具有旋转不变性的信号称为圆信号,反之不具有这一特性的称为非圆信号[21]。若s为均值为零的圆复随机信号,其协方差E[ss*]≠0,伪协方差E[s2]=0;若s为均值为0的非圆信号,则有E[ss*]≠0,E[s2]≠0。对于非圆信号s,其非圆系数γs定义为
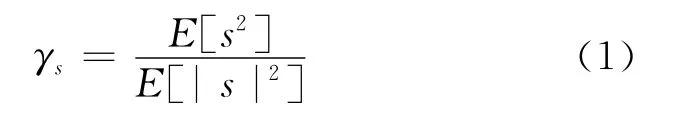
式中:γs=|γs|ejφ,|γs|称为非圆率,φ称为非圆相位。非圆率的取值区间为0≤|γs|≤1,|γs|=0表示信号是圆的,|γs|≠0表示信号是非圆的。特别地,当|γs|=1,信号在星座图直观上看是沿直线分布的,又称为直线信号,如BPSK,MSK信号。
1.2 阵列模型
由于非圆信号一般是窄带信号,本文考虑窄带信号模型。假设1个期望信号和K个干扰信号入射到阵元数为N、阵元间距为半波长的均匀线阵上,信号与干扰两两不相关,各阵元噪声是相互独立、功率相等的空时白噪声,则t时刻阵列接收数据可表示为
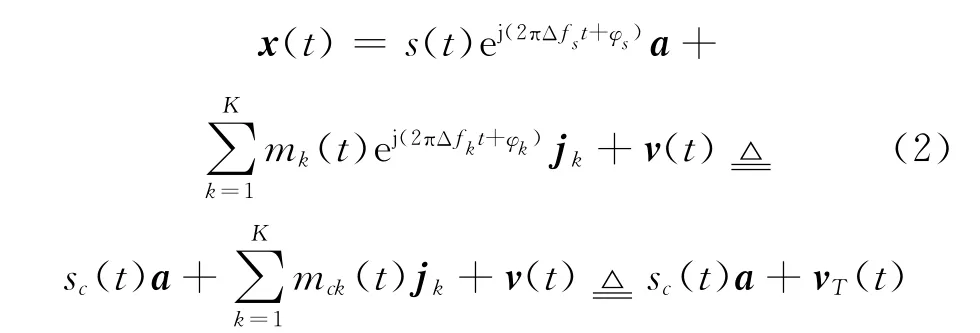
式中:v(t)是噪声矢量,Δfs,a,φs分别是期望信号的偏移频率、导向矢量、载波相位,Δfk,jk,φk分别是第k个干扰的偏移频率、导向矢量、载波相位,s(t)和mk(t)分别是期望信号和第k个干扰的基带波形,sc(t)和mck(t)分别是期望信号和第k个干扰,vT(t)是总干扰噪声矢量。阵列接收的协方差矩阵和伪协方差矩阵分别为

式中:[·]表示在观测时间窗[0,T0]的平均运算,πs、πk分别是信号和第k个干扰的功率,η是噪声功率,IN是一个N×N维的单位矩阵。
由于非圆信号是非平稳信号,因此需要用时间平均的非圆系数代替统计平均的非圆系数。对于期望信号sc(t)=s(t)ej(2πΔfst+φs),将其代入非圆系数的定义式(1),可得时间平均的非圆系数为
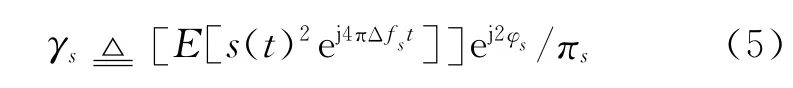
为简单起见,式(5)定义的时间平均非圆系数简称为非圆系数。如果定义sc(t)的本征非圆系数为从式(5)可以看出,|γs|≤|γs,0|。当基带信号s(t)是直线信号时,可以得到
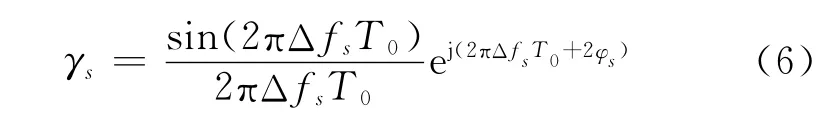
从式(6)可以看出当偏移频率为0时,|γs|=1;当偏移频率不为0时,|γs|是随观测时间变化的;随着ΔfsT0的增大,|γs|趋近于0。
1.3 最小方差无畸变响应波束形成算法
在介绍宽线性波束形成技术之前,先引入Capon提出的最小方差无畸变响应波束形成算法[3],它是宽线性波束形成技术的基础。为了减少阵列对非期望方向上激励的响应,MVDR波束形成算法构造了一个约束最优化问题。这一最优化问题的评判准则为:在期望方向上形成单位幅度增益的前提下,使波束的输出能量最小,用下式描述
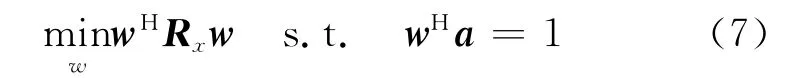
利用拉格朗日乘子法求解上式的最优化问题,可得最优权重矢量
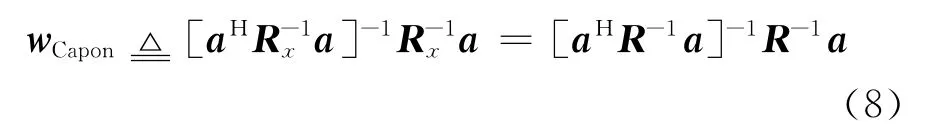
由式(8)可以计算信号的输出功率和干扰加噪声的输出功率,可以很容易地得到MVDR波束形成器的输出信干噪比(Signal to interference and noise ratio,SINR)
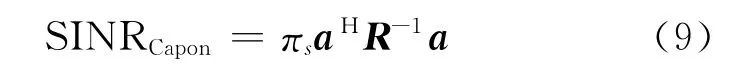
MVDR波束形成算法仅仅利用了观测矢量的协方差矩阵,最多能抑制N-1个干扰。当信号是非圆时,观测矢量还存在伪协方差矩阵,这意味信息没有得到充分利用。如何同时利用非圆信号的协方差矩阵和伪协方差矩阵是宽线性波束形成算法的关键。
2 宽线性波束形成
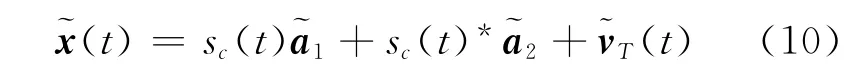
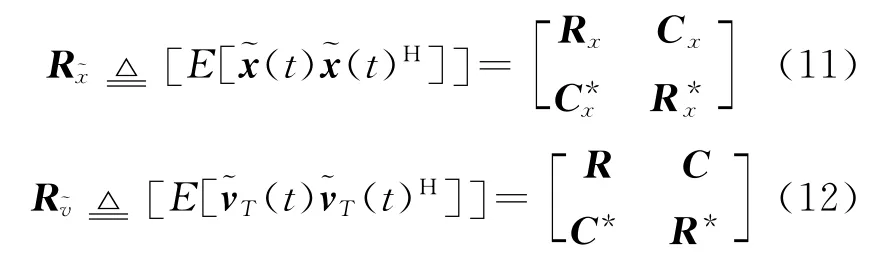
定义扩展的权重矢量为,则阵列的输出形式为
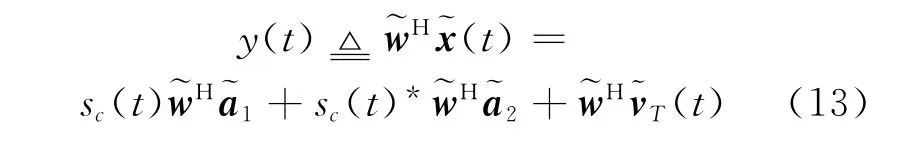
2.1 时不变宽线性最小方差无畸变响应波束形成算法
针对非圆干扰,文献[16]提出了一种时不变宽线性最小方差无畸变响应(TI WL MVDR)波束形成算法。该算法利用线性多约束技术(Linear constraint minimum variance,LCMV)[22],在保证期望方向无畸变响应的情况下,抑制非圆干扰。所以,TI WL MVDR波束形成的约束条件为
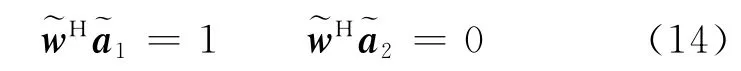
其最优化问题归纳为
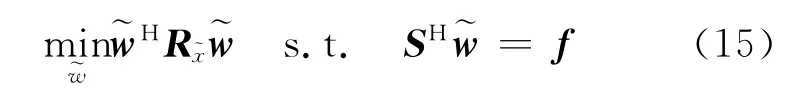
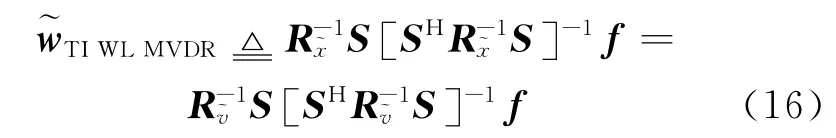
因此,TI WL MVDR波束形成器的输出信干噪比为
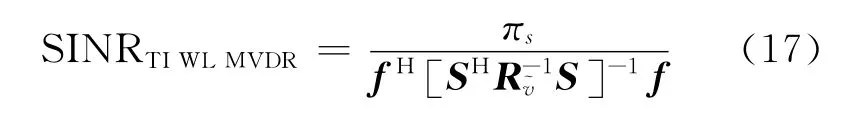
TI WL MVDR波束形成算法扩展了观测矢量维度,最多能抑制N-1+Int(Pr/2)个干扰,式中Int(·)表示取整运算,Pr表示直线干扰的个数。TI WL MVDR波束形成器假设期望信号的非圆性是未知的,而干扰是非圆的,相对于Capon′s MVDR算法,其性能的提升主要来自于对非圆干扰的抑制。由于没有考虑期望信号的非圆特性,因此该算法相对于Capon′s MVDR算法,信干噪比提升不够显著。
2.2 最优宽线性最小方差无畸变响应波束形成算法
为了利用期望信号的非圆特性,文献[17]提出了最优宽线性最小方差无畸变响应(Optimal WL MVDR)波束形成算法,该算法同时利用了信号和干扰的非圆特性,宽线性波束形成器的输出信干噪比相对于Capon′s MVDR波束器有较大提升。
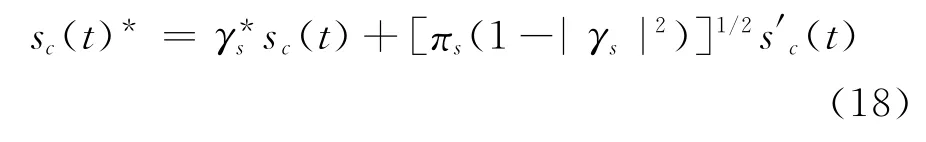
其中s′c(t)是与sc(t)正交的分量,满足
对式(10)应用上述分解,有如下表示
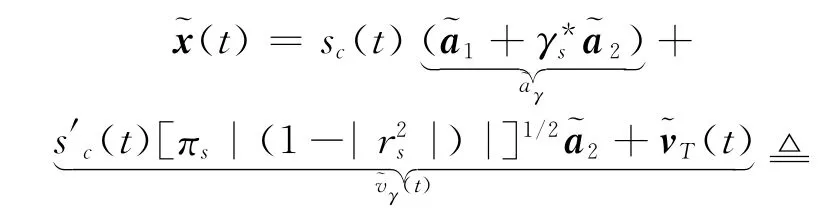
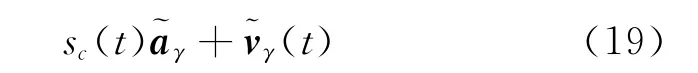
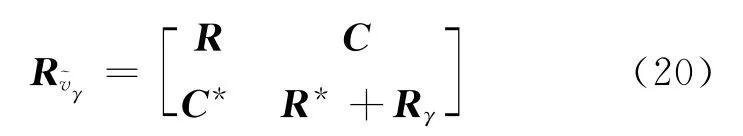
式中:Rγ=πs(1-|γs|2)a*aT。将式(19)代入式(13),宽线性波束形成器输出为
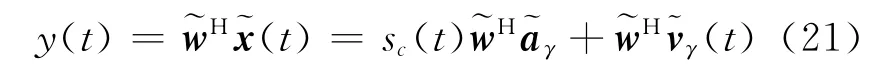
类似Capon′s MVDR算法,最优 WL MVDR波束形成算法的最优化问题归纳为
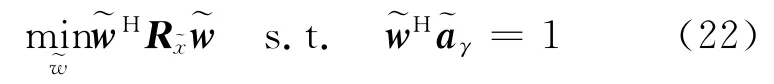
通过拉格朗日乘子法可得最优权重矢量

那么,最优WL MVDR波束形成器的输出信干噪比为
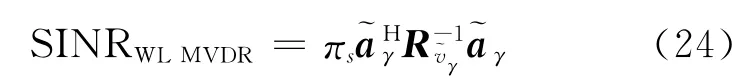
相对于TI WL MVDR波束形成算法,最优WL MVDR波束形成算法同时利用了期望信号和干扰的非圆信息,因此其输出信干噪比明显提升。最优WL MVDR波束形成算法最多能够抑制2(N-1)-Pnr+δ(1-|γs|)个干扰,其中Pnr为非直线干扰的个数对于最优WL MVDR波束形成算法的性能分析,读者可以参阅文献[19]。最优WL MVDR波束形成算法需要已知期望信号的非圆系数,或者通过训练序列估计扩展的导向矢量,估计表达式为式中s0(kTs)是训练序列、L是样本数、Ts是采样间隔。在频谱感知和被动监听中,很难获得期望信号的非圆系数或训练序列,因此该算法存在一定的局限性。
2.3 基于非圆系数估计的宽线性波束形成算法
为了能使最优WL MVDR波束形成算法应用于频谱感知和被动监听领域,需要对非圆系数进行估计。文献[18]提出了一种非圆系数估计算法。
将式(23)代入式(21),可得波束形成器的输出功率
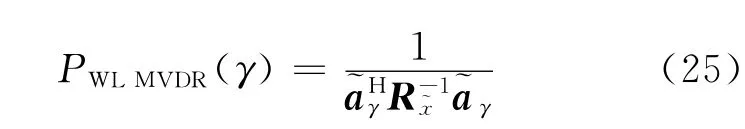
假如将参数γs视为一个变量γ,那么可以通过最大化阵列输出功率来对目标信号的非圆系数进行粗略估计。其最优化问题可以等价为
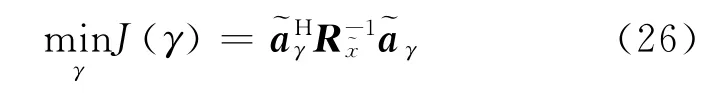
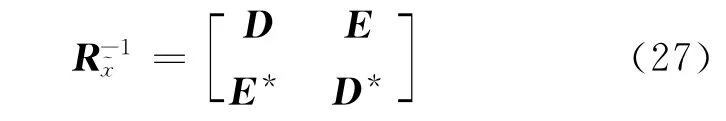
其中
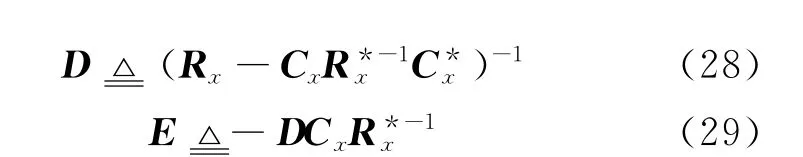
将式(27-29)式代入式(26),可得
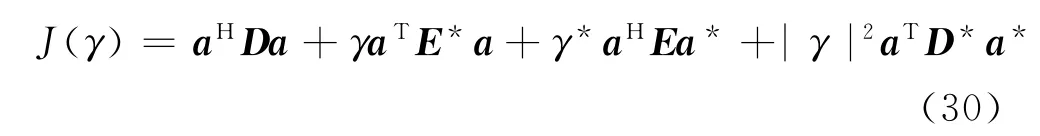
对J(γ)进行求共轭梯度,并令其等于零,可以求得使J(γ)达到最小值的γ值,记为
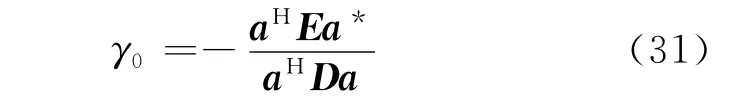
由于J(γ)中包含期望信号、干扰和噪声,仅仅考虑期望信号是不够的。文献[18]的法则1已经证明,当干扰不在波束主瓣内,MVDR类算法的输出功率受干扰的影响比较小。所以可以用一个只包含期望信号和噪声的信号模型来分析γ0受噪声的影响,通过简单的推导,可得

式中:εs≜(aHa)πs/η。一旦估计出期望信号和噪声的功率,就可得到γs的最终估计。其中期望信号功率πs可由Capon功率进行估计,即=1/,噪声功率η可以用协方差矩阵R~x的最小特征值估计。通过进一步分析,可得
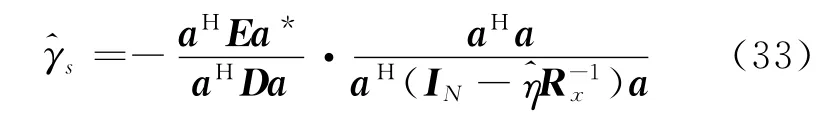
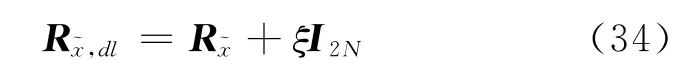
式中:ξ是对角加载等级,一般取10倍的噪声功率[24]。使用对角加载矩阵后,权重矢量为
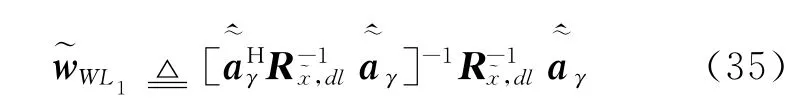
基于非圆系数估计的宽线性波束形成算法解决了非圆系数估计问题,使得最优WL MVDR波束形成算法能应用于实际信号环境。算法的缺点是干扰必须在波束主瓣以外。此外,当干扰数多于阵元数时,不能准确估计期望信号的功率,这会降低期望信号非圆系数的估计精度。
2.4 频移宽线性波束形成算法
载波信号经过下变频后,由于解调频率和载波频率不匹配,会导致期望信号存在偏移频率Δfs。当偏移频率不为0时,期望信号的非圆率小于其本征非圆率,并随观测时间的变长趋近于0。对于最优宽线性波束形成算法,只有当非圆率达到本征非圆率时,其性能才能达到最优[19]。因此如何在观测时间内保持期望信号的最大非圆率,是实现最优性能的关键。
在文献[18]中,使用期望信号的共轭循环相关系数替代非圆系数进行宽线性波束形成。期望信号的共轭循环相关系数定义为
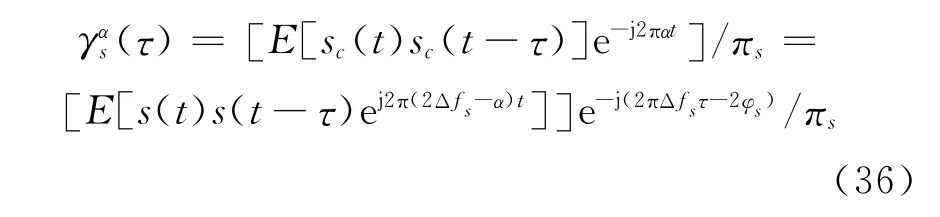
对于直线信号,当(α,τ)=(2Δfs,0),有因此,可以构建一个新的扩展观测矢量将式(2)代入,可得
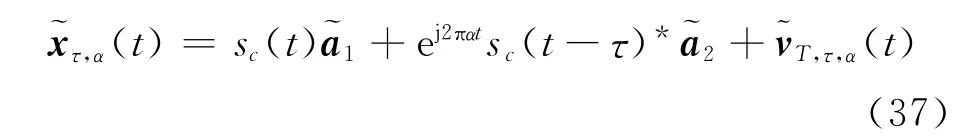
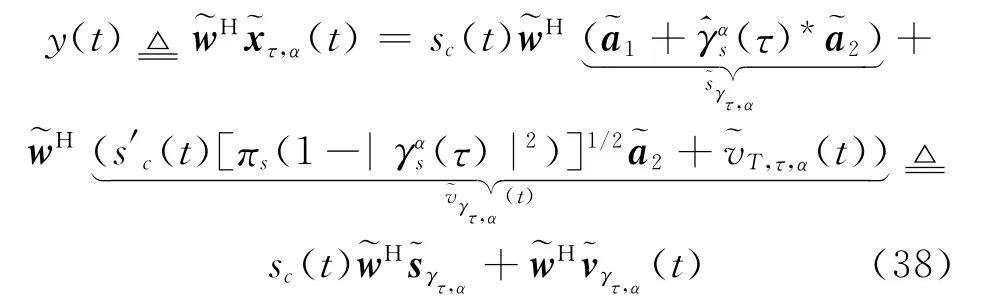
类似最优WL MVDR波束形成算法的推导过程,可得权重矢量
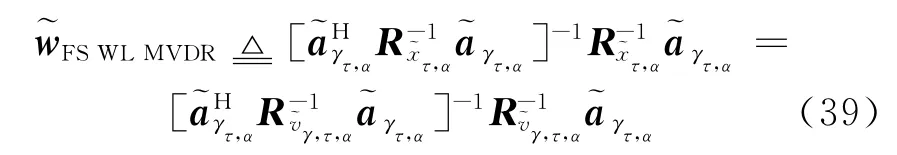
频移宽线性波束形成算法的输出信干噪比为
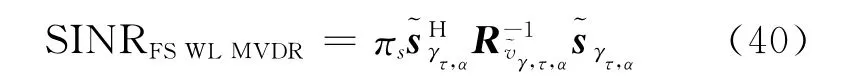
对于共轭循环相关系数(τ)的估计,只需将非圆系数估计算法中的观测矢量换为即可[18]。对于直线信号,(α,τ)=(2Δfs,0),偏移频率可以用文献[18]中的估计算法估计。对于非直线的非圆信号,其循环频率和延时需要用盲估计的方法估计[25-26]。
对于频移宽线性波束形成算法,当期望信号的偏移频率不为0时,其性能优于最优 WL MVDR波束形成器;当期望信号的频偏为0时,其性能等价于最优WL MVDR波束形成算法。此外,该波束形成器也可与对角加载技术结合来提升算法的稳健性。
2.5 基于非圆系数先验知识的稳健宽线性波束形成算法
在实际应用中,当期望信号的名义导向矢量与其真实值之间存在失配或快拍数很少时,波束形成器的性能将会急剧下降。因此,研究者们开始关注稳健宽线性波束形成算法的研究。
文献[20]提出了两种基于不确定约束集的稳健宽线性波束器,在最大化宽线性波束器输出功率的同时,对失配矢量进行约束。第一种方法是对扩展的导向矢量的总误差进行约束,最优化问题表示为
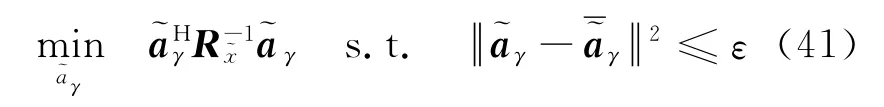
式中:ε是扩展的导向矢量的误差上限ˉγ*sˉaH]T,ˉa是假设的导向矢量,ˉγs是假设的非圆系数。ε与假设的导向矢量误差上限εa和非圆系数误差上限εγ有关,具体的表达形式参考文献[20]。
第二种方法把扩展的导向矢量分成两部分分别进行约束,其最优化问题表示为
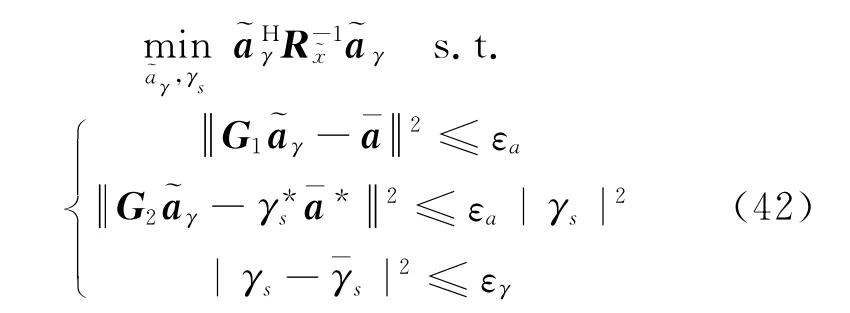
式中:G1和G2是选择矩阵,分别选择扩展的导向矢量的前一半和后一半。需要注意的是,式(41)和式(42)可以利用CVX优化包[27]进行求解。
文献[20]提出的这两种算法在非圆系数误差上限较小时性能较好,当非圆系数误差较大时,性能下降较大。算法的主要缺陷在于需要期望信号的非圆系数先验知识。
3 结 论
为了对宽线性波束形成技术有一个较深的理解,对文中提到的宽线性波束形成算法进行了总结。
非稳健的宽线性波束形成算法:(1)时不变宽线性MVDR波束形成器。该算法仅仅考虑了干扰的非圆特性,没有利用期望信号的非圆特性。(2)最优 WL MVDR波束形成器。该算法同时考虑了期望信号和干扰的非圆特性,相对于MVDR波束器,输出信干噪比明显提升,但是该算法需要已知期望信号的非圆系数,实际应用中很难实现。(3)基于非圆系数估计的宽线性波束形成算法。该算法对期望信号的非圆系数进行了估计,增加了可实用性。(4)频移宽线性波束形成算法。在当期望信号存在非0偏移频率时,该波束形成器优于最优WL MVDR波束器。对于它们的输出信干噪比,有以下关系[17-19]
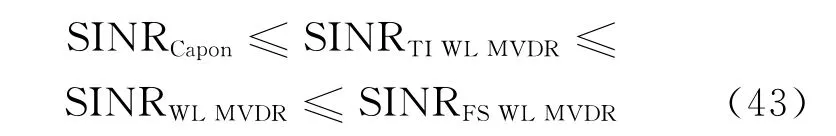
稳健的宽线性波束形成算法:基于非圆系数先验知识的稳健宽线性波束形成算法。该算法需要导向矢量和期望信号非圆系数的预估值和误差上限,实际应用中很难同时获得,并且当非圆系数误差较大时,性能较差。
本文综述的宽线性波束形成算法都要预估期望信号的导向矢量,对于阵列结构已知的场景,只需要预估期望信号相对于阵列的方位角。对于非圆信号的波达方向估计方法,可以参考文献[28-32]。
宽线性波束形成是当前阵列信号处理研究的热点,在通信领域有着广泛的应用。宽线性波束形成的研究已经取得很多成果,然而依然存在许多问题和可以研究的内容:
(1)期望信号的非圆系数估计问题至关重要,虽然文献[18]提出了一种估计方法,但当干扰数超过阵元数或干扰在主瓣内时,非圆系数的估计精度降低。如何在上述情况下给出一个准确的非圆系数估计仍需要进行深入研究。
(2)实际应用中期望信号非圆系数很难有先验知识,各种模型误差下基于非圆系数未知的稳健宽线性波束形成算法有待进一步研究。
(3)由于宽线性波束形成算法相对于传统的线性波束形成算法维数扩展了一倍,其运算复杂度也增加了一倍。如何降低宽线性波束形成的算法复杂度是一个需要解决的问题。
(4)本文所述算法只是基于观测矢量的二阶统计量,如何利用观测矢量的高阶统计量提升宽线性波束形成算法的性能是今后研究的新方向。
[1]Picinbon B.On circularity[J].IEEE Transaction on Signal Processing,1994,42(12):3473-3482.
[2]Wiener N.Extrapolation,interpolation,and smoot-hing of stationary time series:with engineering applications[M].New York:Technology Press of MIT and John Wiley&Sons,1949.
[3]Capon J.High resolution frequency wave number spectrum analysis [J].Proceeding of The IEEE,1969,57(8):1408-1418.
[4]Proakis J G.Digital communications[M].3rd ed.New York:McGraw-Hill,1995.
[5]Chevalier P.Filtrage d′antenne optimal pour signaux non stationnaires-Concepts,performances [C]∥GRETSI.Juan-Les-Pins:[s.n.],1995:233-236.
[6]Chevalier P,Delmas J,Oukaci A.Optimal array processing for nonstationary signals[C]∥IEEE International Conference on Acoustic,Speech and Signal Process.Atlanta:ICASSP,1996:2868-2871.
[7]Chevalier P,Pion F.New insights into optimal widely linear array receivers for the demodulation of BPSK,MSK and GMSK signals corrupted by noncircular iterferences-application to SAIC [J].IEEE Transaction on Signal Processing,2006,54(3):870-883.
[8]Yoon Y,Kim H.An efficient blind multiuser detection for improper DS/CDMA signals [J].IEEE Transaction on Vehicular Technology,2006,55(2):572-582.
[9]Song N,Lamare R,Haardt M,et al.Adaptive widely linear reduced-rank interference suppression based on the multistage Wiener filter [J].IEEE Transaction on Signal Processing,2012,60(8):986-994.
[10]Chevalier P,Pipon F.Optimal array receiver for synchronization of a BPSK signal corrupted by noncircular interferences[C]∥IEEE International Conference on Acoustic,Speech and Signal Process.Toulouse:ICASSP,2006:1061-1064.
[11]Gerstacker C W H,Schober R,Lampe A.Receivers with widely linear processing for frequency-selective channels[J].IEEE Transaction on Communication,2003,51(9):1512-1523.
[12]Schober R,Gerstacker W H,Lampe L.Data-aided and blind stochastic gradient algorithms for widely linear MMSE MAI suppression for DS-CDMA [J].IEEE Transaction on Signal Processing,2004,52(3):746-756.
[13]Buzzi S,Lops M,Tulino A M.A new family of MMSE multiuser rectivers for interference suppression in DS/CDMA systems employing BPSK modulation[J].IEEE Transaction on Communication,2001,49(1):154-167.
[14]Mattera D,Paura L,Sterle F.Widely linear decision-feedback equalizer for time-dispersive linear MIMO channels[J].IEEE Transaction on Signal Processing,2005,53(7):2525-2536.
[15]Aghaei A,Plataniotis K,Pasupathy S.Widely linear MMSE receivers for linear dispersion space-time block-codes[J].IEEE Transaction on Wireless Communication,2010,9(1):8-13.
[16]Chevalier P,Blin A.Widely linear MVDR beamformers for the reception of an unknown signal corrupted by noncircular interferences[J].IEEE Transaction on Signal Processing,2007,55(11):5323-5336.
[17]Chevalier P,Delmas J P,Oukaci A.Optimal widely linear MVDR beamforming for noncircular signals[C]∥IEEE International Conference on Acoustic,Speech and Signal Process.Taipei:ICASSP,2009:3573-3576.
[18]Xu Dongyang,Huang Lei,Xu Xu,et al.Widely linear MVDR beamformers for noncircular signals based on time-averaged second-order noncircularity coefficient Estimation[J].IEEE Transaction on Vehicular Technology,2014,62(7):3219-3227.
[19]Chevalier P,Delmas J P,Oukaci A.Performance analysis of the optimal widely linear MVDR beamformer[C]∥European Signal Processing Conference.Glasgow:[s.n.],2009:587-591.
[20]Wang G,Lie J P,See C S.A robust approach to optimum widely linear MVDR beamformer[C]∥IEEE International Conference on Acoustic,Speech and Signal Process.Kyoto:ICASSP,2012:2593-2596.
[21]刘剑.非圆信号波达方向估计算法研究 [D].长沙:国防科学技术大学,2007.Liu Jian.DOA estimation algorithms for noncircular signal using sensor arrays[D].Changsha:National University of Defense Technology,2007.
[22]Tseng C Y,Griffiths L J.A unified approach to the design of linear constraints in minimum variance adaptive beamformers[J].IEEE Transaction on Antennas Propagation,1992,40(12):1533-1542.
[23]Cox H,Zeskind R M,Owen M H.Robust adaptive beamforming[J].IEEE Transaction on Acoustic,Speech,Signal Processing,1987,35(10):1365-1376.
[24]Carlson B D.Covariance matrix estimation errors and diagonal loading in adaptive arrays[J].IEEE Transaction on Aerospace and Electronic Systems,1988,24(4):397-401.
[25]Zeng X,Ghrayeb A.A blind carrier frequency offset estimation scheme for OFDM systems with constant modulus signaling [J].IEEE Transaction on Communication,2008,56(7):1032-1037.
[26]Ciblat P,Loubaton P,Serpedin E,et al.Performance analysis of blind carrier frequency offset estimators for non-circular transmissions through frequency-selective channels[J].IEEE Transaction on Signal Processing,2002,50(1):130-140.
[27]Grant M,Boyd S,Ye Y Y.CVX:MATLAB software for disciplined convex programming,ver.2.0[EB/OL].http:∥cvxr.com/cvx/May.2013-5-6.
[28]Abeida H,Delmas J.MUSIC-like estimation of direction of arrival for noncircular sources[J].IEEE Transaction on Signal Processing,2006,54(7):.2678-2690.
[29]Gao F,Nallanathan A,Wang Y.Improved MUSIC under the coexistence of both circular and noncircular sources[J].IEEE Transaction on Signal Processing,2008,56(7):3033-3038.
[30]孙心宇,周建江.非圆传播算子DOA估计算法[J].数据采集与处理,2013,28(3):313-318.Sun Xinyu,Zhou Jianjiang.PM method for noncircu-lar signals[J].Journal of Data Acquisition and Processing,2013,28(3):313-318.
[31]郑春弟,冯大政,雷革.一种利用非圆信号特点的实值DOA估计算法[J].数据采集与处理,2009,24(2):193-197.Zheng Chundi,Feng Dazheng,Lei Ge.DOA estimation algorithm for non-circular sources using real-value algorithm [J].Journal of Data Acquisition and Processing,2009,24(2):193-197.
[32]郑春弟,解春维,李有才.基于实值特征值分解的求根 MUSIC算法[J].数据采集与处理,2010,25(2):154-159.Zheng Chundi,Xie Chunwei,Li Youcai.Root MUSIC algorithm based on real-valued eigenvalue decomposition [J].Journal of Data Acquisition and Processing,2010,25(2):154-159.

