一种改进的SURF快速匹配算法
崔振兴,曾 威,杨明强,韩 峰
(山东大学 信息科学与工程学院,山东 济南 250100)
0 引言
在图像处理与计算机视觉中,局部图像特征的描述与检测可以用来帮助辨识物体,因此对物体的局部特征提取具有很重要意义.1999年,Lowe[1]提出了SIFT(scale-invariant feature transform)算法,并在2004年进行了改进[2].SIFT算法用来检测与描述图像中的局部性特征,它在尺度空间中寻找极值点,提取出其位置、尺度、旋转不变量等特征值并生成128维的特征向量.但是由于SIFT统计的是关键点周围邻域的梯度信息,计算复杂度高,并且需要形成128维的高维向量,在特征匹配时耗时巨大,不能达到实时性要求.近年来,基于SIFT改进的算法层出不穷[3-4].为了提高匹配速度,文献[5]提出了主成分分析法(principal component analysis,PCA),运用PCA降低特征向量的维数.为了增强特征描述子的唯一性,文献[6]提出用以关键点作为圆心的同心圆代替棋盘格来计算梯度方向直方图,并计算得到一个272维的特征向量,然后通过主成分分析法将特征向量降成128维.此方法虽然能提高特征向量的独特性,并增加了特征匹配的准确率,但同时也增加了运算时间.Bay等[7]于2006年提出了SURF(speeded up robust features)算法,其速度比SIFT算法提高了3~5倍,准确度也有所提升.在基于视觉的目标识别过程中,人们最关心的问题是识别的准确度和能否实时处理.由于SURF算法特征描述子的维数为64维,与SIFT算法的描述子相比虽然已经减少了很多,但是要达到特征之间的实时匹配仍然显得吃力.相对于SIFT算法,SURF算法在速度上的提升是因为使用了积分图像和盒式滤波器(box filter),但是其在特征点的匹配上仍然采用一一对应相匹配[8].这样,不仅耗时高,而且容易出现误匹配.
本文针对SURF算法,在特征点的形成和匹配方面进行了改进.首先利用图像的Hessian矩阵进行极值点的检测,在确定了极值点之后再利用Haar小波对图像进行计算,得到特征点主方向和64维特征描述子.然后结合特征点的分类思想[9],根据特征点的主方向邻域内像素和之间的差值,形成一个4维的特征向量,与SURF的特征描述子相结合形成新的68维特征向量,以达到提高匹配速度的目的.在匹配时,首先对特征点按照其特征向量的前4维进行粗匹配,从而将特征点分成9组,然后将9组特征点分别进行组内匹配,这样就避免了不同组特征向量之间的相互匹配,从而提高匹配速度和准确率.本文算法流程如图1所示.
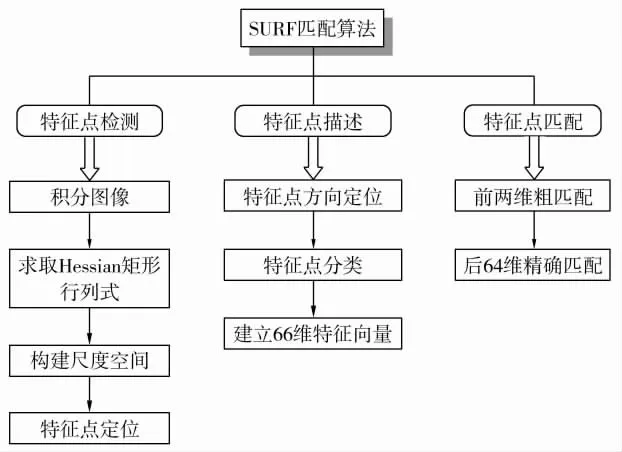
图1 算法流程图Fig.1 Flow chart of the algorithm
1 SURF算法特征点检测
SURF算法的设计步骤基本同于SIFT算法,它基于积分图像提取特征点,并通过Haar小波滤波器来描述特征点,是一种集特征提取和特征描述于一身的算法.SURF算法主要包括3个步骤:特征点检测、特征点描述和特征点匹配.
SURF算法使用近似的 Hessian矩阵[10]来检测特征点,并使用积分图像,大幅度减少了运算量.SURF算法之所以在计算速度上明显快于同类算法,主要是因为它引入了积分图像和盒式滤波器的概念.
1.1 积分图像
积分图像的概念最早是由Viola和Jones[11]提出的,其目的是为了能够快速计算矩形区域的像素和(或者是像素的平方和).它是一种中间图像,通过对原图像遍历即可得到.图2为积分图像示意图.假设图像中的任一点(i,j)的值为I(i,j),则对应积分图像的值IΣ(i,j)为
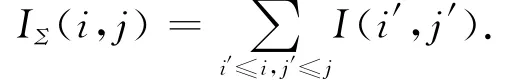
这样,通过积分图像就能够快速地计算图像中任意矩形区域的像素和,且计算的耗时与矩形区域面积大小无关.
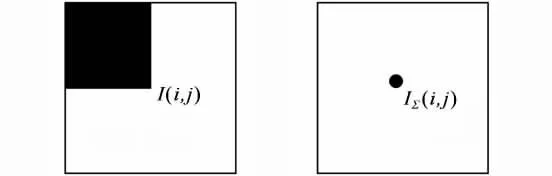
图2 积分图像Fig.2 Integral image
1.2 Hessian矩阵
对给定的一幅图像I,在其任意一点(x,y)处的Hessian矩阵表达式为
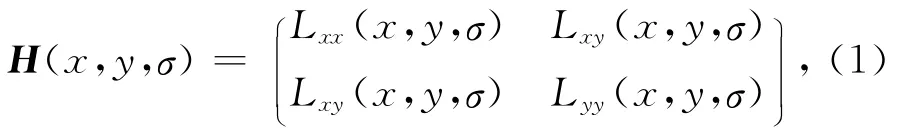
式中Lxx(x,y,σ),Lxy(x,y,σ),Lyy(x,y,σ)分别表示高斯二阶偏导数在点(x,y)处与原图像I的卷积.二维高斯核函数为
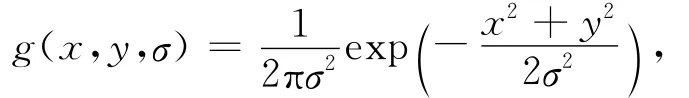
其中σ为标准差.
为了降低复杂度并提高算法的提取速度,Bay在算法中引入了盒式滤波器来近似高斯二阶差分模板.如图3所示,上面一行为高斯二阶差分在xx,yy,xy方向上的模板,下面一行为盒式滤波器对上面一行模板的近似.用Dxx,Dxy,Dyy来近似表示公式(1)中的Lxx,Lxy,Lyy,于是 Hessian矩阵行列式就可以近似表示为
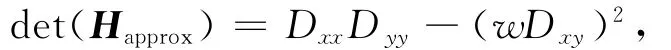
其中w为权重,一般取0.9.用式(1)求图像中每个像素点的响应就可以得到在对应尺度上的响应图.

图3 用盒式滤波器近似高斯滤波器Fig.3 Using box filter to approximate Gaussian filter
1.3 尺度空间
为了使SURF算法具有尺度不变性,可通过改变盒式滤波器的模板大小来建立尺度空间金字塔[12].如图4所示,图像金字塔共分为4层,对每一层进行4次滤波.在第1层中,相邻的模板尺寸相差6个像素,在第2层中相差12个像素,在第3层中相差24个像素,以此类推.每一层的第一个模板尺寸等于其上一层的第二个模板的尺寸.每次滤波对应的近似尺度可由下式计算:

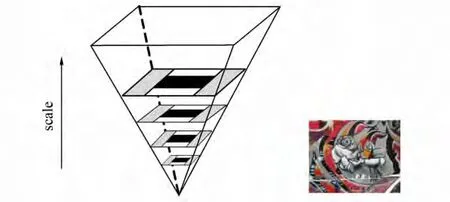
图4 SURF算法尺度空间金字塔Fig.4 Pyramid of scale space
特征点定位:
首先,为Hessian矩阵的响应值设定一个阈值,所有小于这个阈值的点都被去除.
其次,在3×3×3的立体邻域内进行非极大值抑制.只有那些比其上一尺度、下一尺度及本尺度周围的26个点的响应值都大或都小的点才被选为特征点.
最后,通过拟合3维二次函数从而精确确定特征点的位置和尺度.
1.4 特征点主方向定位
为了使SURF特征向量具有旋转不变的特性,需要为SURF特征点确定一个主方向.特征点主方向的确定过程主要分3步(图5):
1)在以特征点为圆心,以6σ(σ为特征点所在的尺度值)为半径的圆形邻域里,用边长为4σ的Haar小波模板[13-14]求x和y两个方向的 Haar小波响应;
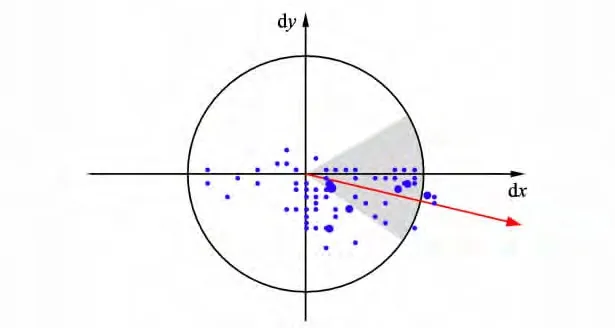
图5 主方向选择Fig.5 Main direction selection
2)以特征点为中心,用标准差为2σ的高斯函数对滤波后的区域进行加权;
3)以关键点为圆心,用一个圆心角为π/3的扇形窗口扫描一周,计算该扇形窗口每个角度内包括的图像点的Haar小波响应总和,取其中最大响应的方向为该关键点的方向.
2 改进SURF算法特征点的描述
2.1 特征点分类
本文算法结合特征点的分类思想,根据特征点主方向邻域内像素和之间的差值形成一个4维的特征向量,与SURF特征描述子相结合形成新的特征向量,进而达到提高速率的目的.
首先,将检测到的特征点在其相应尺度上按照其主方向旋转,将特征点的主方向作为平面直角坐标系xOy中的一个轴,然后以此特征点为圆心,以其所在尺度σ为半径作圆,将此圆形邻域划分为4个区域,分别为平面直角坐标系xOy的4个象限中的像素区域.对于第一象限,以象限内的某一像素点为起点,顺时针遍历象限内的所有点的灰度值至起点,并计算第一象限内所有像素点的灰度值之和Σ1.同理,分别计算Σ2,Σ3,Σ4,如图6所示.
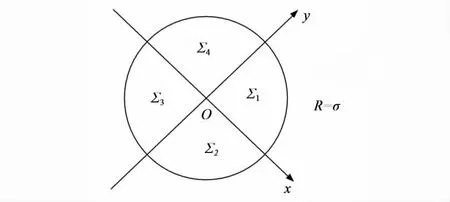
图6 特征点各象限像素点求和示意图Fig.6 Pixel sum in each quadrant
其次,计算Σ13=Σ1-Σ3和Σ24=Σ2-Σ4.设定阈值T0,求出特征向量τi(用二进制数表示):
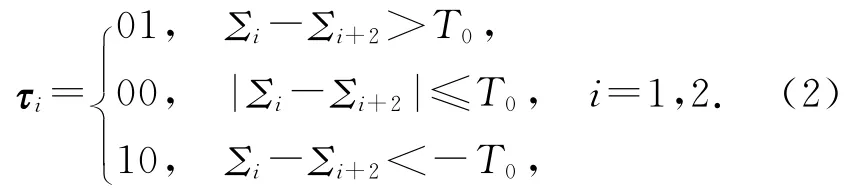
然后将τ1和τ2组合,形成一个4维特征向量.这样,在最后特征点的特征描述子生成之前,先根据τ1和τ2组合将特征点分为9类:0000,0001,0010,0100,0101,0110,1000,1001,1010.
阈值T0的选取原则:选取的阈值T0应该使9类特征点分组中每组特征点的个数尽量相同或者接近,这样可以最大地减小每组匹配耗时.对于不同图像库里的图像,因其特征点的分布不同,故阈值T0的选取也不同.
本文算法与文献[15]中提到的比较描述子思想类似但又不同.通过计算关于特征点对称区域的差值形成描述子,与SURF算法相比,这样计算简单方便,易于后续的特征匹配;而且就比较描述子而言,计算区域之间的差值,能增加描述子的抗噪能力,使匹配更精确.为了增加特征向量的准确度,设置阈值T0,将可以用一位二进制数表示的大小关系变成用两位描述,这样虽然增加了计算复杂度,但是增加了特征点的类别,使后续的匹配更加快速精确.
2.2 建立特征向量
将特征点的主方向作为平面直角坐标系xOy中的一个轴,以其特征点为原点,选取特征点周围的大小为20σ×20σ的矩形邻域,然后将其平均分成4×4个子区域,如图7所示.
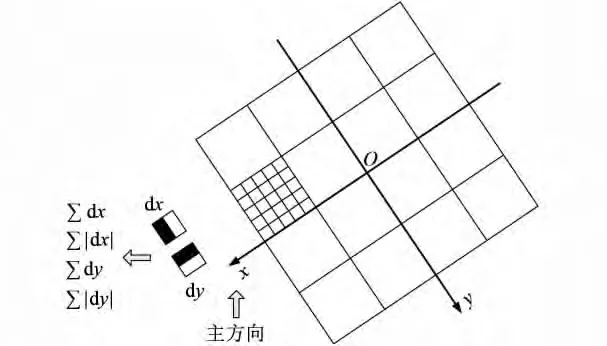
图7 特征描述子的生成示意图Fig.7 Generation of feature descriptor
在大小为5σ×5σ的16个子区域内用窗口尺寸为2σ的Haar小波进行滤波,Haar小波窗口在子区域内均匀移动25次,可得到25组x方向和y方向上的响应值dx,dy;再用标准差为3.3σ的高斯函数对其进行加权,统计子区域内 ∑dx,∑|dx|,∑dy,∑|dy|的值,形成子区域的特征向量;将4×4个子区域内的特征向量组合形成64维的向量;最后,将通过式(2)得到的4维向量与此64维向量结合形成68维向量v,并对此68维向量进行归一化处理,可得到特征点的改进SURF特征描述子.
3 SURF特征点匹配
图像特征提取的直接目的就是特征匹配.本文在提取出SURF特征向量后,首先根据前4维向量对得到的68维特征向量进行粗匹配分组,具体实现过程如下:取出每个特征点形成的68维特征向量v的前4维向量τ1和τ2(其中τ1和τ2都是两维);然后进行同或运算,当两个特征点前4位的同或结果为1111时,将这两个特征点视为同一类.经过一系列的同或运算之后,就可以将特征向量分成9组:0000,0001,0010,0100,0101,0110,1000,1001,1010.最后分别对这9组特征向量进行组内匹配.组内特征匹配的方法有很多,其中用向量的最近邻匹配法[16-17]可以找出潜在的匹配对而无需进行额外信息量的计算.本文算法进行组内匹配时,运用基于BBF搜索方法的最近邻匹配算法来完成对目标的检测和识别.匹配时进行双向匹配.对特征向量进行相似性测量[18],以两个特征向量的欧氏距离[19]作为特征相似的判别标准.设两幅图像I1和I2的SURF特征向量集分别为V1={v11,v12,…,v1m},V2={v21,v22,…,v2n},其中 m,n 分别是两图像上SURF特征点的个数.计算相似特征向量:
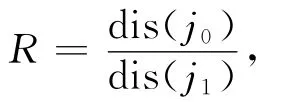
其中
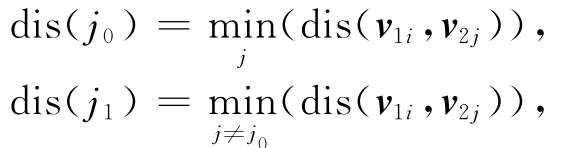
这里dis(v1i,v2j)表示两个特征向量的欧式距离.R即为最小距离与次小距离之比.设定阈值R0,当R>R0时,特征向量匹配不成功,反之则两向量为匹配向量对.
虽然对特征向量的分组会有一定时间损耗,但相比于SURF特征的欧氏距离的运算,这些计算都是少量的加减运算,计算量很小.
4 实验结果及分析
对经典SURF算法与本文改进的SURF算法在特征匹配速度和精度方面进行比较.实验在Windows XP下Matlab 2010a软件中实现.硬件条件为:CPU,Pentium(R)Dual-Core E5800;内 存,2 GB;主频,3.20GHz.
为便于比较,实验中取T0=0,此时公式(2)变为:
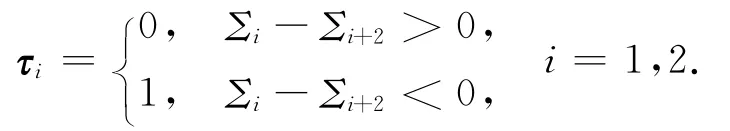
这样特征点被分成00,01,10,11共4组.
在特征向量的形成过程中,对子区域用Haar小波进行滤波,得到25组响应值后需要用高斯函数进行加权.本文从0.1σ开始,以0.1σ个单位递增,在Coil-100图像库中选取每种物体0°和35°两种图像进行验证,求取匹配的平均准确率.
试验结果(表1)表明,当高斯函数的标准差为3.3σ时匹配准确率最高,标准差再增大时准确率不变,因此选用标准差为3.3σ的高斯函数加权.
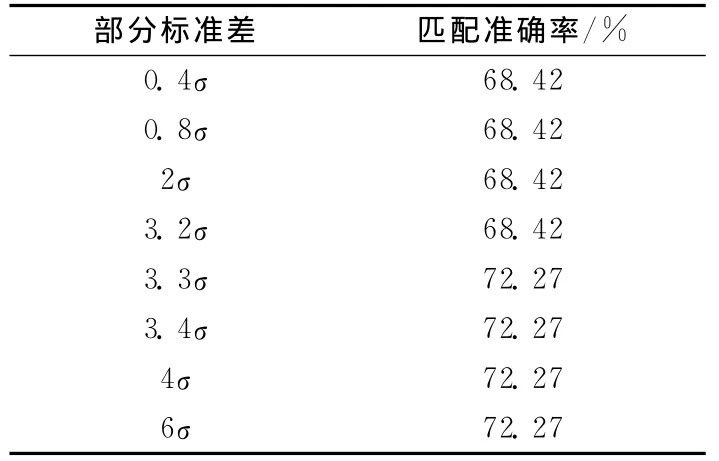
表1 不同高斯标准差对结果的影响Tab.1 Influence of differentσto the results
图8为实验用的原始图像与提取SURF特征后的图像,第一行为一对具有较强仿射变化和旋转变化同时相似性又较强的原始图像,图像大小为800像素×640像素.第二行为采用本文算法提取特征点后对应图像的特征点信息在图像上的显示,其中“·”,“+”,“△”,“*”分别表示4组特征向量.

图8 原始图像与提取SURF特征后的图像Fig.8 Original figure and SURF feature points
表2为原始图像的特征点信息.可以看出,本文算法在提取出的图像特征点上与经典SURF算法一致,即不会减少从原图像中提取出的特征点数目.

表2 原始图像提取特征点的数目Tab.2 Number of the feature points
在提取出特征点之后,对原始图像进行特征点的匹配(图9).图像为object0024.view01.jpg和object0024.view03.jpg.图像大小均为640像素×480像素,分辨率为96dpi.表3为按照本文算法分组后的两幅图像各自的特征点个数及匹配耗时.可以看出,本文算法实现两幅原始图像特征点的匹配耗时为0.046s,同时,本文算法在分组时所消耗的时间为0.009s,所以总耗时为0.046+0.009=0.054s.本文算法在速度与精度上较经典SURF算法都有一定提高,具体比较结果如表4所示.

图9 匹配结果图Fig.9 Matching results

表3 原始图像特征点分组情况及匹配耗时Tab.3 Group of the feature points and matching time-consuming

表4 本文算法与经典SURF算法对比结果Tab.4 Comparation of the two algorithms
可以看出,本文的改进算法比经典SURF算法所消耗的时间少0.090s,而正确匹配率也因为降低了噪声干扰而比经典SURF算法高.
为了验证本文算法在特征点提取与匹配方面的普遍适用性,在哥伦比亚大学的Coil-100图像库中做实验验证.Coil-100图像库为100种不同物体的各个不同视角不同尺度的图像.从Coil-100图像库中随机挑选30种不同物体,分别取其视角为0°,5°,10°,15°,20°,25°,30°,35°,40°,45°的10种图像进行特征匹配,取每次实验数据的平均值作为最后的结果,并与经典SURF算法相比较.图10为其中一组图像0°和35°的原图、特征点提取图及匹配结果图.结果显示,SURF算法平均匹配耗时为0.008s,而本文算法为0.005s.
由于Coil-100数据库中图像大小为128像素×128像素,提取特征点的数目也较少,因此用经典SURF算法匹配耗时比较短,准确率也较高,但从平均匹配耗时和图11仍然可以看出,在Coil-100图像库中,相较于经典SURF算法,本文算法在精确度不下降的情况下匹配时间仍有明显提高.

图10 原始图、特征点提取图及匹配结果图Fig.10 Original figure,feature points and matching results
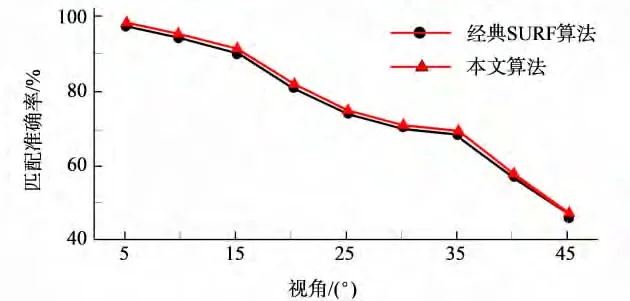
图11 两种算法在Coil-100库的匹配准确率Fig.11 Accurate of the two algorithms based on Coil-100
5 结语
经典SURF算法在匹配的过程中,对一幅图像上每一个选定的特征点都要与另一幅图像上所有的特征点一一进行匹配,耗时较高.基于此,本文提出了将特征点分组匹配的改进方法,根据特征点邻域内像素之间的差值形成一个4维的特征向量,与SURF的特征描述子相结合,以达到提高匹配速度和准确率的目的.通过对改进算法的理论分析和实验验证,结果表明:相对于经典SURF算法,本文算法在速度上有明显的提高,精确度也有所改善,更适用于对实时性要求较高的图像配准,如基于单目视觉的智能服务机器人的目标识别过程中,本文算法可以提高其目标识别的速度,以达到实时性要求.
[1]Lowe D G.Object recognition from local scale-invariant features[C]//7th International Conference on Computer Vision.September 20-25,Corfu,Greece.IEEE,1999,2:1150.
[2]Lowe D G.Distinctive image features from scale-invariant feature points[J].Int J Comput Vision,2004,60:91.
[3]胡海青,谭建龙.改进SIFT算法在文字图像匹配中的应用[J].计算机工程,2013,39(1):239.
[4]王民,刘伟光.基于改进SIFT特征的双目图像匹配算法[J].计算机工程与应用,2013,49(2):203.
[5]Ke Y,Sukthankar R.PCA-SIFT:a more distinctive representation for local image descriptors[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition.June 27-July 02,Washington DC,USA.IEEE,2004,2:506-513.
[6]Viola P,Jones M.Rapid object detection using a boosted cascade of simple features[C]//Proceedings of the 2001IEEE Computer Society Conference on Computer Vision and Pattern Recognition.December 08-14,Kauai,Hawaii.IEEE,2001,1:511-518.
[7]Bay H,Ess A,Tuytelaars T.SURF:speeded up robust features[J].Computer Vision & Image Understanding,2008,110(3):346.
[8]杜冬梅,王红旗,田昆鹏.一种改进的快速SURF算法[J].科学技术与工程,2013,13(5):1350.
[9]黄诗捷,王定祥,张征宇.一种同名像点快速匹配方法[J].兵工自动化,2012,31(3):51.
[10]康长青,袁磊,华丽.一种新的血管造影图像Hessian矩阵增强算法[J].计算机工程与科学,2012,34(10):104.
[11]Viola P,Jones M J.Robust real-time face detection[J].Int J Comput Vision,2004,57(2):137.
[12]方亦凯,程健.基于快速尺度空间特征检测的手势识别方法[J].图像图形学报,2009,14(2):214.
[13]陈景航,杨宜民.一种基于Harr小波的快速模板匹配算法[J].计算机工程,2005,31(22):167.
[14]赵沁平,车英慧.基于Harr小波的动态场景全频阴影绘制算法[J].软件学报,2011,22(8):1948.
[15]Rublee E,Rabaud V,Konolige K.ORB:an efficient alternative to SIFT or SURF[C]//IEEE International Conference on Computer Vision.Nov 6-13,Barcelona.IEEE,2011:2564-2571.
[16]蔡贺,张睿.k最近邻域分类算法分析与研究[J].甘肃科技,2012,28(18):14.
[17]赵璐璐,耿国华,李康.基于SURF和快速近似最近邻搜索的图像匹配算法[J].计算机应用研究,2013,30(3):921.
[18]贾克斌,方晟,沈兰荪.基于颜色和空间特征的彩色图像获取方法[J].电子学报,2003,31(6):895.
[19]刘相滨,邹北骥,王胜春.一种新的完全欧氏距离变换算法[J].计算机工程与应用,2005,41(13):44.

