类Mg离子的电子关联效应研究
胡 峰
(徐州工程学院 数学与物理科学学院,江苏 徐州 221111)
在天体物理和实验室物理中,已经观测到了类Mg离子的光谱,特别是其中的互组合线对于了解星际和实验室等离子体密度的变化和基本过程有重要的意义.为了解释观测到的现象,就要得到精确的类Mg离子的参数,例如跃迁能量、振子强度、跃迁几率等.近些年来,人们对类Mg离子已经做了大量的实验和理论研究,例如:在实验方面,Fawcett用激光产生的等离子体研究了低Z类 Mg离子[1],而Sugar、Churilov以及Litezén等[2-4]完成了高Z 类 Mg离子的研究.在理论方面,Froese Fisher等利用多组态 Hatree-Fock(MCHF)方法研究了Z=12~92类Mg离子的特性[5],Huang等用多组态相关任意相位近似(MCRRPA)研究了Z=12~22类Mg离子的激发能和振子强度[6],Bulter等利用R矩阵方法研究了选定的类Mg离子的能量(Z=12~14,16,18,20,26,28)[7-8],Chen等用组态相互作用(CI)研究了类 Mg离子的能级以及光电离截面[9],Tayal等用基于 CI方法的CIV3程序计算了(Z=20,24,29)类 Mg离子的能级和跃迁特性[10-12],Kang等利用多组态Dirac-Hartree-Fock方法研究了3s3p(3P0)能级的超精细结构[13],青波等利用构建全相对论的准完备基方法计算了Mg的能级,获得了很好的结果[14].最近Massacrier等利用FAC程序研究了Sc的相关类Mg离子的特性[15].但是,我们注意到很多理论结果和实验结果存在一定的差距,以及部分结果是以图的形式出现的,并不能够获取准确的数据.本文选取类Mg的Z=20~24的离子为研究对象,这些离子研究数据较少[5-6],且存在上述提到的2个原因,因此利用多组态Dirac-Fock(MCDF)方法,通过考虑电子关联效应,去获得更加精确的数据和理解差距产生的原因.
所谓电子关联效应,就是指价电子与原子实内的电子之间的相互作用.国外已经有大量的文献报道[6,16-17],我们小组也做了相应的工作[18-20].研究表明,电子关联效应对于原子的能级结构和跃迁特性有很大的影响,考虑了电子关联效应后能够获得更加精确的数据.本文主要研究类Mg离子的特性,这些离子闭壳层外有2个价电子,是典型电子关联效应研究的对象.和先前工作一样,我们选取基于多组态Dirac-Fock方法的GRASPVU程序包来进行计算.
1 理论计算方法
1.1 波函数和能级的计算
多组态Dirac-Fock理论方法在文献[21]中已有详细描述,这里仅作扼要的介绍.在多组态Dirac-Fock理论中,一个核电荷数为Z、具有N个电子的原子或离子体系的Dirac-Coulomb哈密顿量(原子单位)为

这里的^Hi是第i个电子的Dirac哈密顿量,可表示为
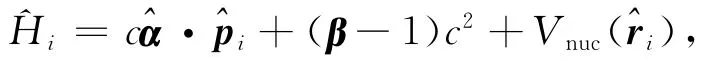
其中Vnuc()是核势场和β分别是Dirac矢量和标量矩阵是第i个电子的动量算符,c是真空中光速.在中心场近似下单电子的旋轨波函数[22]可表示为
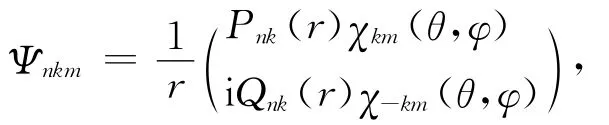
式中k为Dirac量子数,Pnk(r)和Qnk(r)分别为相对论径向波函数的大小分量,χkm为自旋函数.
N电子体系的组态波函数|Γr(PJM)〉是所有单电子旋轨波函数组成的N阶Slater行列式波函数|Ψp〉的线性组合,即
在MCDF方法中,任一原子态α的波函数|α(PJM)〉由具有相同P,J和M 量子数的组态波函数|Γr(PJM)〉线性组合而成,即

式中nc是组态波函数的个数,Cr(α)为组态混合系数.
对角化由原子波函数(1)式构造的哈密顿矩阵,则可得到相关原子态的能量和组态混合系数.对于其它高阶效应,如Breit修正和主要的量子电动力学QED效应,可作为微扰处理.
1.2 电子关联效应
在具体计算过程中,主要是通过逐渐增加基矢数目来考虑更多的组态相互作用,直至得到收敛的结果.可以把组态相互作用分为两类:
VV关联(valence-valence correlation) 价电子之间的相互作用.
CV关联(core-valence correlation) 原子实内的电子与价电子之间的相互作用.实际上描述的是原子实的极化效应.
一般来说,只考虑VV关联就能得到比较精确的结果,但是对于电子数目比较多的体系,如果要得到更精确的结构,则CV关联是必须考虑的.在本文的计算中,这2种关联都进行了考虑.
1.3 计算步骤
文献[17-21]已经详细介绍了电子关联作用,这里只作简单介绍.计算中考虑电子关联效应的2个步骤如下:
1)运行Dirac-Fock,初步得到1s22s22p63s2的径向波函数.在这一步里,选用Thomas-Fermi模型势作为计算的初始波函数.在自洽场计算中,对所有的轨道都进行了优化.
2)让n=1~2为闭壳层,也就是说主量子数为1和2的轨道上的电子是封闭的,既不允许这些电子向其它轨道跃迁也不允许其它轨道的电子跃迁到这2个轨道.允许n=3的轨道上一个电子可以跃迁到n=4,5,6,7轨道上,且任意分布,这样就考虑了VV关联,其扩展的轨道形式为1s22s22p6nln′l′.而对于CV关联来说,我们考虑2种情况,一种是2p轨道上一个电子不受限制,另一种是2s上一个电子不受限制.此时我们要求对于一个双激发,一个电子必须来自原子实中的2p(2s)轨道,另一个电子必须来自价电子.这样原子实n=2轨道电子和价电子之间的CV关联作用就考虑进去了,其扩展的轨道形式为1s22snl2p6n′l′n″l″和1s22s22p5nln′l′n″l″.
2 结果与讨论
2.1 能级
表1给出了基于MCDF方法的VV和CV 2种模型下类 Mg离子3s3p(3P0,1,2,1P1)的能级,结果包含了量子电动力学效应和特殊质量位移,其中量子电动力学效应考虑了2种修正:自能和真空极化.表1的实验结果来自于NIST[23].考虑电子关联效应后,组态波函数急剧增加,这对于计算的收敛性和程序本身的计算能力、计算时间要求相对提高很多,因此在保证计算精度的条件下,有必要对扩展的主量子数进行限制.对于VV模型,主量子数限定在n≤7,其对应的最大波函数数目为698;CV模型n≤6,其波函数数为13 069.尽管对主量子数进行了限制,计算的结果仍然可信,这是因为本文的结果正是建立在增加波函数基矢数目的基础上来考虑电子关联效应的.
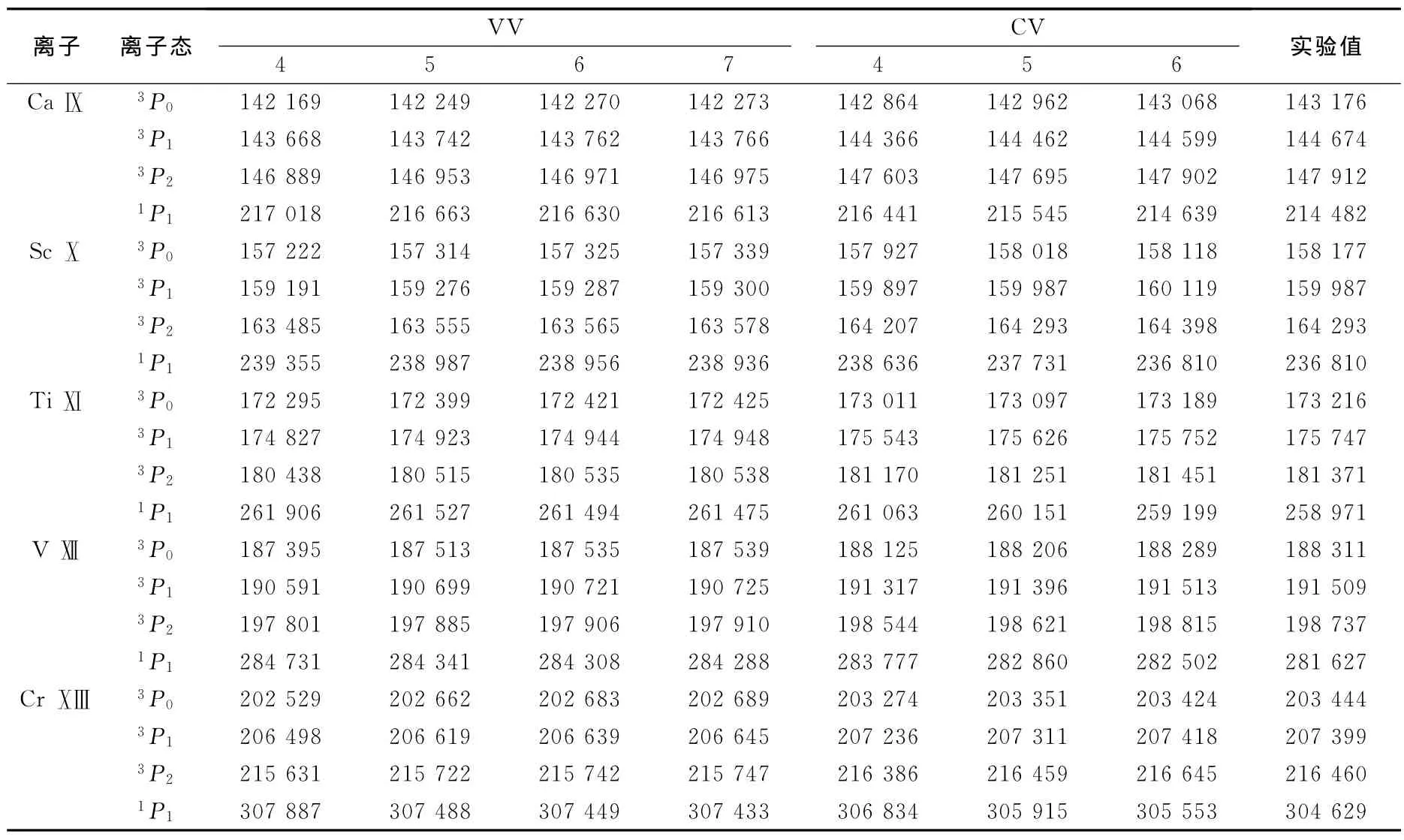
表1 类Mg的离子的3s3p能级Tab.1 The energies of Mg-like 3s3p levels cm-1
从表1可以看出,CV的结果更加接近于实验值.若不考虑1P1能级,VV的计算值与实验值的偏差在0.21%~0.76%之间,而CV的偏差在0.001%~0.040%之间.CV模型下的1P1能级与实验值的偏差则在0.01%~0.31%之间,但是如果没有考虑电子关联效应,1P1的能级与实验值偏差在0.89%~0.99%之间,因此可认为,考虑电子关联效应后,CV计算的能级与实验值符合得很好.为了更好地说明电子关联效应对1P1能级的影响,图1给出了随扩展主量子数变化的VV,CV与实验值的偏差(ΔE=E计算值-E实验值).
总之,对于2种模型来说,随着主量子数的扩大,2种模型的结果与实验值更加接近,但是对于VV模型来说,n=6与n=7的结果最大偏差只有22cm-1,也就是说n=7的轨道对于3s2和3s3p能级的影响相当小,也从一个侧面说明了当前计算对于主量子数的限制是可行的.同时可以发现,高n层的旁观电子对于计算的结果有很大的影响,CV模型更为明显,这点在我们先前的文章中也有类似的结论[18-20].
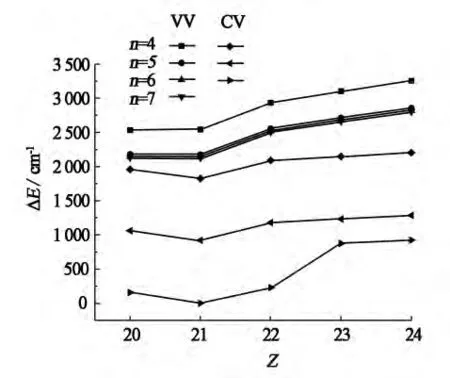
图1 电子关联效应对1 P1能级的影响Fig.1 The electron correlation on 1 P1energy level
为了说明当前计算结果是可信的,在表2中比较了不同方法计算出的类Mg离子的CaⅨ能级值.其中CIV3的计算结果是由Tayal等[10]由基于组态相互作用的CIV3程序给出的,SST的结果来自Tayal[24],BCF的结果是Fawcett[1]利用Cowan程序给出的,而 MCHF的结果则是由Tachieve等[5]给出的.从表2可以看出,CV的计算值要优于CIV3,SST,MCHF的,大部分优于BCF的;同时,我们注意到,对于1P1能级而言,除了BCF结果外,其它理论结果与实验值偏差都有点大.总之,考虑了电子关联效应后,CV值要优于其它理论计算值.

表2 CaⅨ能级的实验值和理论计算值Tab.2 The experimental and theoretical results of CaⅨ cm-1
2.2 波长
分析低密度等离子体中发射的自旋禁戒谱线的信息是诊断等离子体温度和密度的很好手段之一,因此,准确的波长对于研究等离子体的状态是必不可少的.为了验证当前计算的可信性,表3给出了Z=20~24的类Mg离子的理论值和实验值,其中实验值来自文献[23,25-26],MCHF来自[5].从表3可以看出,2种模型和MCHF方法给出的CaⅨ~CrⅩⅢ离子1S0-3P1跃迁波长都比实验值偏高,其中 VV 偏高在0.116 1~0.332 2nm 之间,CV偏高在0.001 4~0.030 5nm之间,而 MCHF偏高在0.148 0~0.235 8nm之间.CV与实验值的最大偏差为0.034nm,明显好于MCHF和VV的计算值,因此认为考虑电子关联效应后,提高了波长的精度.
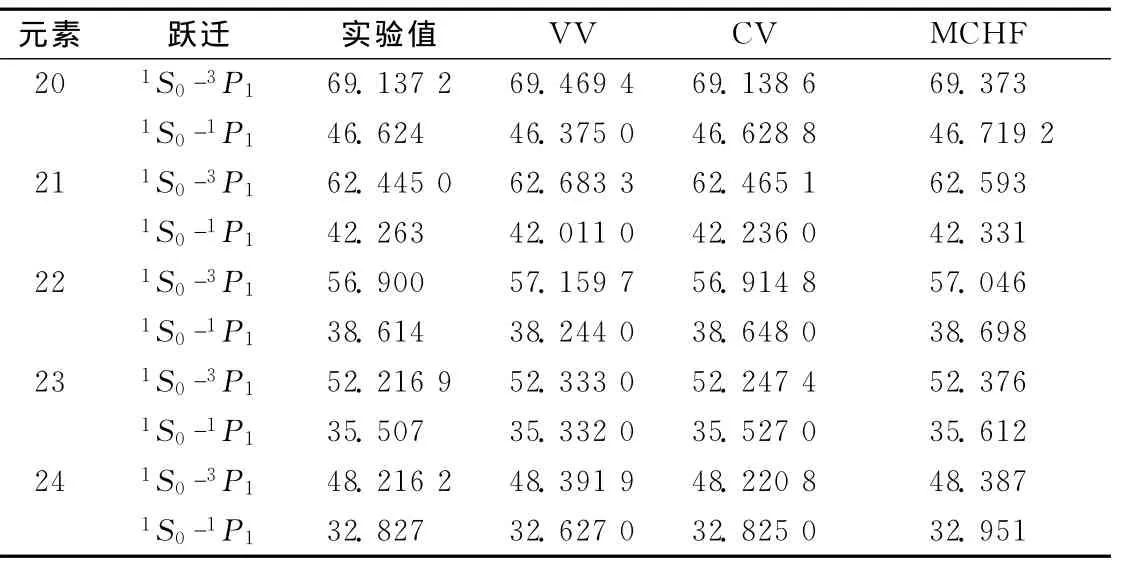
表3 类Mg离子(CaⅨ~CrⅩⅢ)的波长Tab.3 The wavelengths of Mg-like ions(CaⅨ~CrⅩⅢ) nm
2.3 振子强度
从i态到j态跃迁的振子强度和跃迁几率的关系公式[27]如下:

其中m和e分别是电子质量和电荷,c是光速,λji是跃迁波长(nm),ωi和ωj分别是下能级i和上能级j的权重(简并度).对于电偶极跃迁(E1)来说,跃迁几率和振子强度可以给出如下的形式:

其中S是线强度,单位为原子单位(au).
表4给出了类 Mg离子的3s2-3s3p(3P1,1P1)跃迁的振子强度,同时也给出了来自 MCHF[5]、Safronova等[28]以及 Huang等[6]的结果.

表4 类 Mg离子3s2-3s3p(3 P1,1 P1)跃迁的振子强度(表中数据a(b)为a×10b 的缩写)Tab.4 The oscillator strengths of 3s2-3s3p(3 P1,1 P1)transitions of Mg-like ions
可以看出,类Mg离子1S0-1P1跃迁的振子强度随元素序数的增加而减少.MBPT的计算值要低于其它所有理论的计算值,但是随着元素序数的增加,偏差也在逐渐缩小.VV,CV,MCHF以及Huang的结果大体在一个数量级上,彼此之间的偏差不超过10%.NIST给出的CaⅨ,ScⅩ以及TiⅪ1S0-1P1跃迁的振子强度分别为1.10,1.05和0.993,这些值与CV给出的结果符合得很好(小于1.44%).Huang等的结果与NIST给出的结果相差也小于1%,因此可以通过比较CV与Huang等的结果来确保当前计算的可信性.可以看出,CV的计算值与Huang等的结果数值上很接近,因此认为当前的计算是可信而且准确的.
2.4 能级寿命
算的准确性.因此在表5和表6分别给出了3s3p(3P1和1P1)的能级寿命,其中,表格中的拟合值为Curtis在1991年根据当时的实验值和一些理论结果拟合产生的[29].对于3P1,VV的计算结果与拟合值偏差为1.89%~8.89%,CV 与拟合值的偏差为1.09%~2.23%,MCHF与拟合值的偏差为3.83%~11.0%,而MBPT与拟合值的偏差为4.73%~25.4%.可以看出,考虑电子关联效应后,CV的计算值与拟合值更加接近.对于CrⅫ,如果考虑NIST[23]给出的5.55×10-8s,则CV与实验值的偏差仅为0.36%.
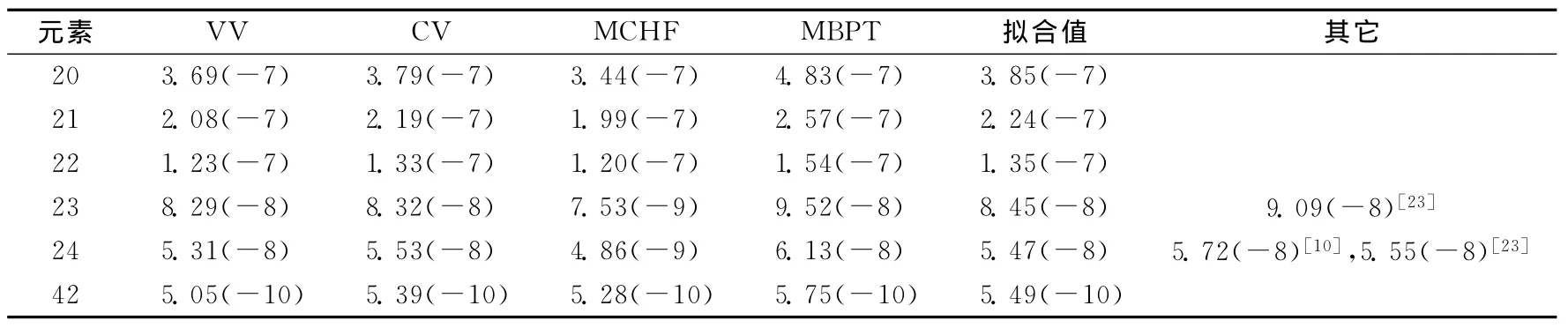
表5 类Mg离子3 P1的能级寿命Tab.5 The lifetimes of Mg-like ions 3 P1energy levels

表6 类Mg离子1 P1的能级寿命Tab.6 The lifetimes of Mg-like ions 1 P1energy level 10-11 s
对于类Mg离子1P1的能级寿命而言,我们发现理论值与拟合值的符合要比3P1的情况要好,VV的计算结果与拟合值偏差为1.50%~6.68%,CV与拟合值的偏差为0.29%~0.56%,MBPT与拟合值的偏差为7.48%~12.3%,MCHF与拟合值的偏差为4.77%~8.83%.同时注意到表5和表6中NIST给出的实验值与拟合值有0.29%~6.94%的偏差,我们认为有2个原因,一是NIST给出的实验值,其自身的不确定度就在20%;二是当时拟合时,实验数据较少,因而拟合点少造成拟合公式不是很精确.如果考虑这2个因素,我们认为考虑电子关联效应后,CV的值是可信的.但是由于类Mg的实验大多是在1980年代完成的,受制于当时条件,造成实验精度不是很高,因此,能级寿命的测量需要更加精确的实验来完成.
3 结语
本文在MCDF方法的基础上,考虑电子关联效应,详细计算了类Mg离子的能级、波长、振子强度和能级寿命,结果表明考虑电子关联效应后,当前CV的结果与已有的实验结果及理论结果符合很好.这些结果对于理解类Mg离子的不同效应有重要的意义,同时对于分析已有的实验结果和指导未来的实验也有重要的意义.然而,需要指出的是当前计算结果是在重点考虑3s2和3s3p组态基础上给出的,因此,可以看出本文的一些计算结果与实验值仍有一定的差距,在今后的计算中,需要更多的组态以获得更好的结果.
[1]Fawcett B C.Calculated oscillator strengths and wavelengths for allowed transitions within the third shell for ions in the Mg-like isoelectronic sequence between SⅤand NiⅩⅦ[J].At Data Nucl Data Tables,1983,28(3):579.
[2]Suagr J,Kaufman V.Copper spectra in a laser-generated plasma:measurements and classifications of CuⅫto CuⅩⅪ[J].J Opt Soc Am B,1986,3(5):704.
[3]Chrilov S S,Levashov V E,Wyart J F.Extended analysis of the 3d2-3p3dtransitions in the sequence KⅧ-CuⅩⅧand isoelectronic trends in Mg-like ions through KrⅩⅩⅤ[J].Phys Scr,1989,40(5):625.
[4]Litzén U,Redfors A.Fine structure splitting of the term 3s3p24Pin Al-like ions[J].Phys Lett A,1988,127(2):88.
[5]Tachieve G,Fischer Froese C.MCHF/MCDHF database[DB/OL].[2014-03-10].http://www.vuse.vanderbilt.edu/~cff/mchf_ collection/.
[6]Huang K N,Johnson W R.Resonance transition of Mg-and Zn-like ions from multiconfiguration relativistic random-phase approximation[J].Nucl Instrum Methods Phys Res B,1985,9(4):502.
[7]Bulter K,Mendoza C,Zeippen C J.Atomic data for opacity calculations.ⅩⅨThe magnesium isoelectronic sequence[J].J Phys B:At Mol Opt Phys,1993,26(23):4409.
[8]Hudson C E,Norrington P H,Ramsbottom C A,et al.Dirac R-matrix collision strengths and effective collision strengths for transitions of NiⅩⅦ[J].Astron Astrophys,2012,537:A12.
[9]Chen M H,Cheng K T.Large-scale relativistic configuration-interaction calculations of the 3s21S0-3s3p1,3P1transitions[J].Phys Rev A,1997,55(5):3440.
[10]Tayval V,Gupta G P,Msezane A Z.Excitation energies,oscillator strengths and lifetimes in CaⅨ[J].Phys Scr,2005,71(6):627.
[11]Tayval V,Gupta G P.Fine-structure energy levels,oscillator strengths and lifetimes in Mg-like chromium[J].Eur phys J D,2007,44(3):449.
[12]Tayval V,Gupta G P.Fine-structure energy levels,oscillator strengths and lifetimes in CuⅩⅧ[J].Phys Scr,2009,80(5):055301.
[13]Kang Huihui,Li Jiguang,Dong Chenzhong,et al.Hyperfine quenching of the 3s3p3P0level in the Mg-like ions[J].J Phys B:At Mol Opt Phys,2009,42(19),195002.
[14]青波,程诚,高翔,等.全相对论多组态原子结构及物理量的精密计算——构建准完备基以及组态相互作用[J].物理学报,2010,59(7):4547.
[15]Massacrier G,Artru M C.Extensive spectroscopic data for multiply ionized scandium:ScⅢto ScⅩⅪ[J].Astron Astrophys,2012,538:A52.
[16]Jönsson P,Froese Fisher C.Accurate multiconfiguration Dirac-Fock calculations of transition probabilities in the Mg isoelectronic sequence[J].J Phys B:At Mol Opt Phys,1997,30(24):5861.
[17]Chen M H,Cheng T K.A large-scale relativistic configuration-interaction approach:application to the 4s2-4s4p transition energies and E1rates for Zn-like ions[J].J Phys B:At Mol Opt Phys,2010,43(7):074019.
[18]Hu Feng,Jiang Gang,Yang Jiamin,et al.Multiconfiguration Dirac-Hartree-Fock(MCDHF)calculations for Zn-like sequence fromZ=48to 54[J].Chin Phys B,2011,20(6):063103.
[19]Hu Feng,Yang Jiamin,Wang Chuanke,et al.Multiconfihuration Dirac-Fock calculations in multi-valence-electron systems:benchmarks on Ga-like ions[J].Phys Rev A,2011,84(4):042506.
[20]胡峰,杨家敏,王传珂,等.电子关联效应对金离子的影响[J].物理学报,2011,60(10):103104.
[21]Song Shuqiang,Peng Feng,Jiang Gang.Properties of K-alpha and K-beta X-ray transitions in CuⅩⅩthrough CuⅩⅩⅧ[J].J Phys B:At Mol Opt Phys,2006,39(1):2087.
[22]王晶,刘凯,王道光,等.高离化态镁的 Kα线理论研究[J].徐州师范大学学报:自然科学版,2009,27(2):59.
[23]Kramida A,Ralchenko Y,Reader J,et al.NIST atomic spectra database[DB/OL].[2014-03-10].http://physics.nist.gov/PhysRefData/ASD.
[24]Tayal S S.Oscillator strengths for ArⅦ,CaⅨ and FeⅩⅤ[J].J Phys B:At Mol Opt Phys,1986,19(10):3421.
[25]Seely J F,Ekberg J O,Feldman U,et al.Wavelengths for the 3s21S0-3s3p3P1transition of the magnesium like ions Fe14+through Nd48+[J].J Opt Soc Am B,1998,5(3):602.
[26]Sugar J,Kaufman V,Indelicato P,et al.Analysis of magnesium like spectra from CuⅩⅧto MoⅩⅩⅪ[J].J Opt Soc Am B,1986,6(1):1437.
[27]Aggarwal K M,Keenan F P.Energy levels,radiative rates and electron impact excitation rates for transitions in He-like FeⅩⅩⅤ,CO ⅩⅩⅥ,NiⅩⅩⅦ,CuⅩⅩⅦand ZnⅩⅩⅨ[J].Phys Scr,2013,87(5):055302.
[28]Safronova U I,Johnson W R,Berry H G.Excitation energies and transition rates in magnesiumlike ions[J].Phys Rev A,2000,61(5):052503.
[29]Curtis L J.Isoelectronic smoothing of line strengths in intermediate coupling[J].Phys Scr,1991,43(2):137.
[30]Froese Fisher C,Godefroid M.Short-range interactions involving plunging configurations of the n=3singlet complex in the Mg sequence[J].Phys Scr,1982,25(2):394.

