偏心拉杆极值应力的电测法研究
蔡瑜玮,李顺才,吴明明
(江苏师范大学 机电学院,江苏 徐州 221116)
当杆件所受外力作用线与杆轴线平行但与轴线不重合时,将使杆产生偏心拉伸或压缩现象[1],承受偏心拉压的构件在工程中很常见.杆件承受偏心拉压时由于存在附加的弯曲变形,其变形属于轴向拉伸(或压缩)与弯曲的组合变形,因此,杆件横截面危险点的应力往往高于单一轴向拉伸时的应力,导致杆件承载能力的降低,其影响的程度则由偏心距来决定[2].在对工程结构和机器的零部件进行设计或理论计算时,常需要用电测法测定作用力的大小与方位.电测应力、应变试验方法(简称电测法),不仅用于验证材料力学的理论、测定材料的机械性能,而且作为重要的试验手段为解决工程问题及从事研究工作,提供良好的试验基础.电测法的基本原理是将电阻应变片(简称应变片)粘贴在被测构件的表面,当构件发生变形时,应变片随着构件一起变形,应变片的电阻值将发生相应的变化,通过电阻应变仪可测量出应变片中电阻值的变化,并换算成应变值,或输出与应变成正比的模拟电信号(电压或电流),用记录仪记录下来,也可用计算机按预定的要求进行数据处理,得到所需要的应变或应力值[3-4].电测法属于无损伤测试,它使用的测试设备和电阻应变片的安装工艺比较简单,而且测量精确度高,因此电测法在工程测试中很常用.如赵德平等用电阻应变法测定了圆形、圆环形、矩形和口字形截面杆在偏心拉伸或压缩时的作用力及其方位,同时给出了不同的贴片方案和一、二次加载方法,结合力学理论推导出计算偏心拉压作用力及其方位的公式[5];孙斌祥[6]研究了偏心拉杆存在应力损伤时的极限承载能力;曹万林等[7]研究了往复偏心拉压荷载下矩形钢管混凝土柱的工作性能;阴存欣[8]研究了异形截面钢筋混凝土偏心拉压构件承载能力分析的电算法,并编制了相应的程序.本文通过电测法测试偏心拉杆的极限拉、压应力,并与理论应力值进行对比来验证本文中电测法的可靠性.
1 偏心拉杆危险点应力的理论公式
所用的偏心拉杆如图1所示(图中数据单位均为mm),中间等截面段的横截面面积为A=30mm×5mm,试件两端通过∅8mm的插销孔与加载装置连接,偏心拉力为F,偏心距e=10mm.对于试件中段的任意横截面,其内力有轴力N及弯矩M,且

横截面上由轴力N引起的正应力及弯矩M 引起的最大正应力分别为

其中抗弯截面模量Wz=×5×303mm3=11 2502 mm3.
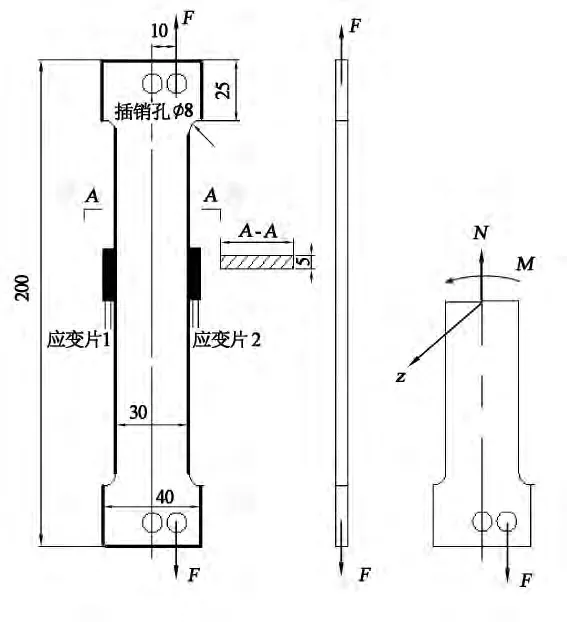
图1 偏心拉伸试件Fig.1 Eccentric tensile specimen
由图1可知,杆件最左侧、最右侧棱边上的点为危险点,对应的最大压应力、最大拉应力分别为

若以εN,εM分别表示由轴力和弯矩产生的正应变,根据胡克定律σ=Eε,可得

在试件的边缘沿轴向粘贴电阻应变片1,2,它们的电阻值为R,灵敏系数K=2.03,应变片1,2在偏心载荷F作用下的工作应变ε1F,ε2F为

由式(2)可得

则弹性模量为

2 设备及原理
偏心拉杆电测法的主要试验设备有:材料力学多功能试验台、XL2118A型应变综合参数测试仪.电阻应变测量法的关键技术之一是惠斯通电桥桥路的设计,如图2所示,其中E1是电源电动势,UBD是桥路的输出电压,R1~R4为4个阻值相同的应变片.

图2 惠斯通电桥Fig.2 Wheatstone bridge
设电桥4个桥臂的应变分别为ε1,ε2,ε3,ε4,应变片的灵敏度系数为K,则

εd为电阻应变仪的读数,即

常用的桥式测量电路有1/4桥(半桥单臂)、半桥双臂、全桥对臂和全桥4臂测量桥路.测试中一般根据实际情况需要进行各种方式的组桥,恰当的组桥方式不仅可以消除因载荷偏心造成的影响,也可以消除由于温度变化带来的影响,提高灵敏度.本次试验中试件表面粘贴两枚应变片,可采用1/4桥、半桥和全桥对臂等桥路来完成应力的测试.
2.1 方案1——半桥单臂测量
如图3所示,将承受机械变形的工作片接入AB桥臂,BC桥臂接公共温度补偿片,其他两臂接应变仪内部标准电阻.

图3 半桥单臂测量Fig.3 Half bridge-single arm measure
设环境温度变化引起的温度应变为εt,则当应变片1与应变片2单独接入AB桥臂时,根据式(5)可得应变仪读数分别为

式(6)表明,采用半桥单臂测量时,应变仪的读数即为每枚工作片在偏心载荷作用下的实际应变值.结合式(3)可计算杆件材料的拉压弹性模量,结合式(4)可计算危险点应力σ1,σ2,且

2.2 方案2——半桥双臂及全桥对臂测量
半桥双臂测量电路如图4所示,应变片1,2分别接入AB与BC桥臂,其他两臂接应变仪内部标准电阻.

图4 半桥双臂测量Fig.4 Half bridge-dual arm measure
根据式(5)可得应变仪读数为

式(8)表明,采用半桥双臂测量时,应变仪的读数即为弯矩应变εM大小的负2倍.
全桥对臂测量如图5所示,应变片1,2分别接入AB与CD桥臂,其他两臂接温度补偿片.

图5 全桥对臂测量Fig.5 Full bridge-opposite arm measure
根据式(5)可得应变仪读数为

式(9)表明,采用全桥对臂测量时,应变仪的读数是轴力所产生拉应变εN的2倍.
由式(8),(9)测到应变εN,εM后,即可由式(2)计算ε1F,ε2F.进一步,由式(7)计算得到应变片1,2的工作应力σ1,σ2.
3 试验步骤
1)测量试件的尺寸,按式(1)计算危险点的理论应力值,按图1粘贴两枚应变片.
2)安装试样,调整机上、下铰座距离至合适高度.按试验要求接好电路、调试仪器、检查整个系统是否处于正常工作状态.
3)按半桥单臂桥路接线,测定材料的弹性模量及试件的危险点应力.均匀缓慢加载至初载荷,记下应变片的初始读数,然后分级等增量加载,依次记录各级载荷作用下应变的读数,直到载荷达到预设值.重复3次后卸载.
4)分别按半桥双臂、全桥对臂桥路接线,按上述方法加载,测定轴力及附加弯矩引起的拉伸应变,该2种方案的试验重复2次.
5)试验结束后,卸掉载荷,仔细观察试件的变化.关闭电源,整理好所用仪器设备,清理试验现场并将设备复原.
4 结果及分析
半桥单臂方案中应变片1与应变片2的3次记录及平均值如表1所示,半桥双臂及全桥对臂方案中应变εN,εM的2次试验记录及平均值见表2.
利用表1及式(4)可求得弹性模量并取均值得到E1=215GPa.再由式(7)计算得到半桥单臂方案中应变片1,2的工作应力,如表3所示.表3中应力的理论值由式(1)计算.
由表2中的载荷及εN均值,利用式(4)可计算得到表2方案中弹性模量的均值为E2=216GPa.将表2中εN,εM的平均值代入式(2),求得ε1F,ε2F,再由式(7)及E2,求得方案2中应变片1,2的工作应力σ1,σ2,并分别计算试验所得应力与理论值的相对误差,结果见表3.
根据表3,方案1与方案2中σ1的相对误差均值分别为3.8%,4.5%;σ2的相对误差均值分别为1.2%,1.4%.因此,第1种方案优于第2种方案,而且绝大部分载荷下2种试验方案的相对误差都小于5%,说明本文中的试验方案是可行的.

表1 半桥单臂试验结果Tab.1 Experimental result by the half bridge-single arm method

表2 半桥双臂及全桥对臂试验记录Tab.2 Experimental results by the half bridge-dual arm method and full bridge-opposite arm method

表3 应力理论值与各方案试验值对比结果Tab.3 Comparison of theoretical values with experimental values of each scheme
5 结论
在偏心拉杆两侧分别粘贴一枚应变片,通过电阻应变测量法,采用2种方案测得了偏心拉杆横截面上危险点的应力.第1种方案采用半桥单臂电桥直接测得材料的杨氏弹性模量及极值应力;第2种方案采用半桥双臂电桥、全桥对臂电桥分别测得轴向力及附加弯矩单独作用下的轴向线应变,然后叠加得到危险点的总应变及极值应力.2种试验方案所得应力值与理论解非常接近,验证了本文中电测试验方法的可行性.
[1]刘鸿文.材料力学[M].北京:高等教育出版社,2008.
[2]邱克.材料力学[M].北京:国防工业出版社,2009.
[3]潘少川,刘耀乙,钱浩生.试验应力分析[M].北京:高等教育出版社,1988.
[4]陈健华.试验应力分析[M].北京:中国铁道出版社,1984.
[5]赵德平,毕杰春.偏心拉压作用力及其方位的测定方法[J].沈阳工业大学学报,1999,21(6):541.
[6]孙斌祥.偏心拉伸的应力损伤分析和承载能力研究[J].工程力学,2001,18(增刊):397.
[7]曹万林,段修斌,张境洁,等.往复偏心拉压荷载下矩形钢管混凝土柱工作性能研究[J].结构工程师,2012,28(4):133.
[8]阴存欣.异形截面钢筋混凝土偏心拉压构件承载能力分析的电算方法[J].城市道桥与防洪,2009(12):117.

