类比法在高等数学教学中的应用

朱彩兰

（江海职业技术学院基础部，江苏扬州，225101）

所谓类比，就是根据两个对象之间的某些相同或相似的性质，推断它们在其他方面也可能具有相同或相似的性质的一种思想方法。按照哲学的观点，万事万物之间都是有联系的，既然有联系，那么必然有联系点即类比点。在教学中只要我们找到合理的类比点，可以说就较为准确地找到了学生的“最近发展区”，这样学生会较为顺利地依次达到他们的“最近发展区”，从而较大限度地挖掘他们的潜能。

一、类比法教学的教育意义

通过类比法教学，既使学生更易掌握新知识，又有助于培养学生以下方面的能力。

（一）培养发现问题的能力

爱因斯坦曾经说过：“提出一个问题往往比解决一个问题更重要，因为解决问题也许仅仅是一个数学上或实验上的技能而已。而提出新的问题、新的可能性，从新的角度去看旧的问题，却需要创造性的想象力，而且标志着科学的真正进步。”[1]既然事物之间是有联系的，通过与某一事物的类比会发现另一事物的某一方面的特点，使得类比成为发现问题的一个重要源泉。通过类比来提出问题，不仅可以使学生温故知新，而且可以帮助学生更好地理解、记忆和运用所学的知识。

（二）提高分析问题的能力

世界上没有能够解决一切问题的“万能钥匙”。学生的人生各阶段必然会遇到各种各样、甚至稀奇古怪的问题，其中一些问题还可能是教师所没遇到过，这样的问题如何解决，就需要他们自己去分析思考，他们也只能在已有知识的基础上去寻求解决新问题的办法，而利用旧知识去解决新问题就需要寻求新问题与旧知识的类比点，进而发现解决新问题的方法。

（三）提高创新能力

虽然世间万事万物是有联系的，但是关键在于找到它们之间有价值的联系，只要找到它们之间本质的联系点，才可能有所创新。如建筑设计师在设计高层建筑物时需要考虑高层建筑在外力（如风力）的影响下发生震动而产生的安全问题，这个问题的解决就是通过与弹簧的震动作类比来解决的[2]。在科学研究中合理的运用类比法，不仅可以创新地解决新问题，还可以有新的发明创造，如木匠用的锯，据说就是鲁班根据自己被带齿的草叶划破手与锯断木头作类比而发明的，类比的重要性就在于它是发明的源泉之一。

二、《高等数学》类比法教学程序

高等数学的核心内容是一元函数微积分与多元函数微积分，在教学中可以根据一元函数与多元函数都是描述一个变量与另外（一个或多个）变量之间的关系这一相同点，由一元函数的知识通过类比，猜测多元函数也可能具有相同或相似的结论，然后再去验证这些结论，其教学程序如图1所示。

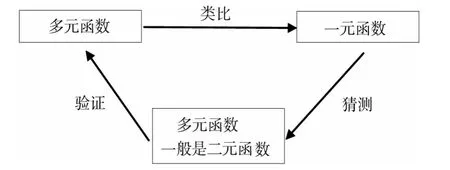
图1 类比法教学程序示意图

三、类比教学法的应用举例与教学效果的显现

（一）关于不定积分的分部积分法

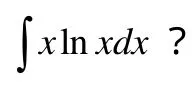
（二）关于积分区间（域）的可加性

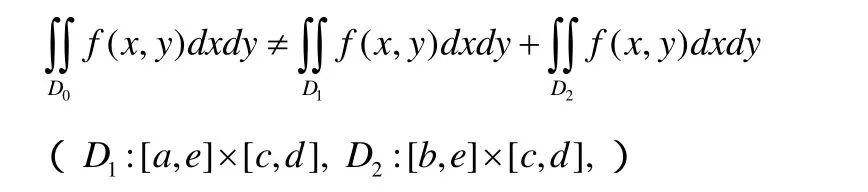
但对于图5有

[1]爱因斯坦，英费而德.物理学的进化[M].上海：上海科技出版社，1962.

[2]戴朝寿，孙世良.数学建摸简明教程[M].北京：高等教育出版社，2007：20-21.

[3]余敏.类比思维在高等数学中的应用[J].河南广播电视大学学报，2012(4)：103-104.

[4]张莉，檀结庆，唐烁，等.高等数学课堂教学与一题多解[J].大学数学，2012(6)：144-148.

[5]华东师范大学数学系.数学分析（上、下册）[M].北京：高等教育出版社，1991.