土力学中关于土的强度理论的计算分析

许多文

(武威职业学院，甘肃武威 733000)

土力学中关于土的强度理论涉及三个方面的问题:土中一点的应力计算，土的极限平衡状态和极限平衡条件。很多的资料和参考书中，直接给定了应力计算结果的解析表达式，而对于其得出的过程鲜有推导。对于土的极限平衡条件，根据图解法中的相切关系，求解主应力之间的逆向关系式也是省略的。所以，如何更加完整又准确的诠释土力学中一点的应力状态及其推导过程，如何运用微元思想与数学工具采取定性描述与定量表达相结合的数学模型来求解，及极限平衡条件下的逆向主应力求解和判断技巧都是亟需补充与解决的问题。

1 土中一点的应力状态

1.1 解析法

材料力学中，设从受力物体内某点取出一单元体，它的前后两个面上的应力等于零，其他两对互相垂直的面上分别作用着已知的应力，即在X截面(外法线与X轴平行的截面)上作用着应力σx，τx，在Y截面(外法线与 Y轴平行的截面)上作用着应力 σy，τy。这些应力均与XY平面相平行。这种应力状态一般为平面应力状态。为了方便起见，将该单元体用平面图表示，如图1a)所示。应力的符号规定为，正应力以拉应力为正而压应力为负，切应力以对单元体内任一点顺时针转为正，反之为负。在图1a)中的 σx，σy，τx皆为正值，而 τy为负值，并且根据切应力互等定理有τx= － τy。

现在研究与单元体前后两面垂直的斜截面ef，ef截面的外法线n和x轴的夹角为α，以后称此截面为α截面，并规定α角由x轴逆时针转到n时为正。用ef截面将单元体截开，并取efb部分来研究其平衡见图1b)。α截面上的应力用σα和τα表示，并均设为正值。ef截面的面积用dA表示，则eb和bf截面的面积分别为dAcosα和dAsinα。取n和t为参考坐标轴见图1b)，写出平衡方程:

图1 应力平面数力分析图

由此可得:

根据切应力互等定理可知，τx和τy数值相等;又由三角公式可知:

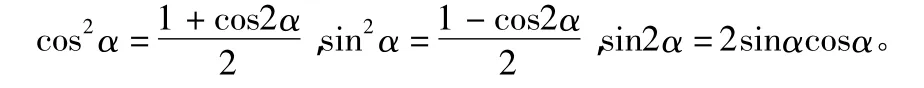
将上述关系式代入式(1)和式(2)，于是得:

以上两式为平面应力状态下斜截面上应力表达的一般公式。应力公式应用时，要注意应力及其斜面方位角的正负。此方法为解析法。

1.2 图解法

平面应力状态下，除了用解析表达式(3)和式(4)来确定斜截面上应力σα和τα，还可以用解析法演变而来的图解法求解。其推导过程如下:

式(3)变形得:

此圆即为应力圆或莫尔圆。单元体的任一截面上的应力与应力圆上的点坐标存在一一对应的关系。在土力学中，假设某面积为dxdz的一土体单元，作用着大小主应力σ1和σ3，见图2b)，则在土体内与大主应力σ1作用平面成任意角α的平面上的正应力σα和τα可以用τ—σ坐标系中直径为(σ1－σ3)的应力圆上的一点(逆时针旋转2α，见图2a)中的A点)的坐标来表示。

式(5)左、右两边平方加上式(4)左、右两边平方，得:

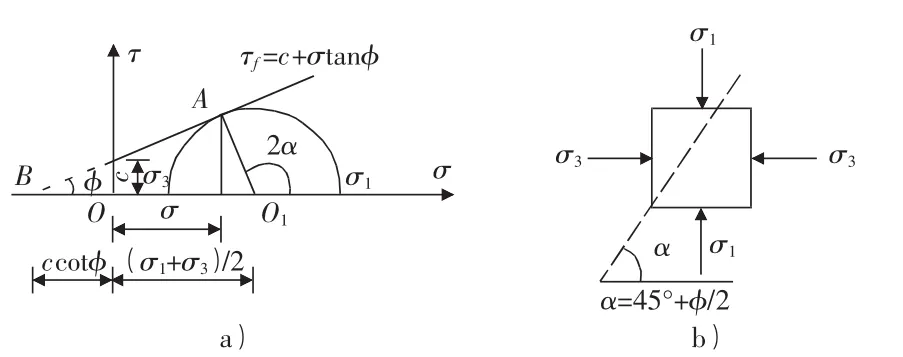
图2 应力圆与库仑强度线关系图

故求解中，对照于式(6)，相对于在土力学中 τx=0，σ1=σy，σ3= σx，得:

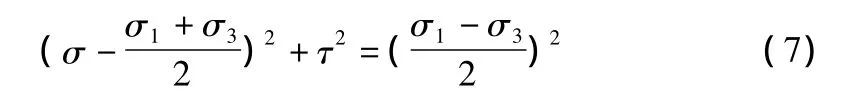
2 土的极限平衡状态

如果把代表土中某点应力状态的莫尔应力圆，与该土的库仑强度线画在同一个τ—σ坐标图中，根据图形之间的相对位置关系，共有三种状态:相切，相离和相割。相切是表明该点处于极限平衡状态，见图3。相离是指莫尔应力圆位于库仑强度线的下方，说明通过该点任意平面上的剪应力都小于土的抗剪强度，因此不会发生剪切破坏。相割实际上是不复存在，因为该点土体已经被破坏。

图3 极限平衡状态判断图

3 土的极限平衡条件

3.1 推导过程

对照于图3中，根据极限应力圆与强度线相切于A点的几何关系，将抗剪强度线延长与σ轴相交于B点，由直角三角形ABO1可知:

由此得:

化简并通过三角函数间的变换(万能公式、和差角公式)从而得到土的极限平衡条件时主应力之间的关系表达式:

由直角三角形ABO1内角与外角的关系可得:

3.2 极限平衡状态判断

极限平衡状态判断中，已知条件给出了土样内摩擦角φ和粘聚力c，大主应力σ1和小主应力σ3，此时是否达到极限平衡状态，判断见图 3。由 σ1→σ3f时，比较若得 σ3f＜ σ3，则有半径，故该土样未达到极限平衡状态;反之，则发生了剪切破坏。由 σ3→σ1f时，比较若得 σ1＜σ1f，则有半径，故该土样未达到极限平衡状态;反之，则发生了剪切破坏。

4 结语

土力学中某点的应力状态其计算值理论仍溯源到材料力学中平面应力状态的求解，待分析土体中任一点的主应力方向与之相反，但计算原理一致，并且解析法是计算的基础，图解法为外在图形表达，所以力学分析的思想是一脉相承的。土的极限平衡状态是从库仑强度线与莫尔应力圆的图形位置关系上来判定，直观明了。根据最大、最小主应力及土体的抗剪强度指标来判断土的极限平衡条件，实为逆向求解的过程。整个土的强度理论的计算过程充分运用了数学工具的微元体思想、万能公式及和差角公式等，对于相关的土力学理论学习有很好的借鉴意义。

［1］董建国，沈锡英，钟才根.土力学与地基基础［M］.上海:同济大学出版社，2011:138-141.

［2］付红梅.土力学与地基基础［M］.西安:西安交通大学出版社，2011:74-75.

［3］苏振超，张丽娜.建筑力学［M］.西安:西安交通大学出版社，2012:393-397.