巧用“8”字形和“A”字形解决问题

杨翠荣

（敦化市第三中学，吉林 敦化 133700）

问题引入（一）：如图（1）点 P是⊿ABC内任意一点，连接BP、CP，试探究：∠P与∠1、∠2有什么关系？

常见的方法是延长BP交AC于点D，不难发现∠BPC=∠2+∠PDC, 而∠PDC=∠1 +∠A;由此可得∠BPC=∠2 +∠1+∠A.

构建模型：若将线段BC去掉，得到的模型类似于“A”字形，由上面的原理可知，只要具备“A”字形的问题，都可用其结论解决问题。

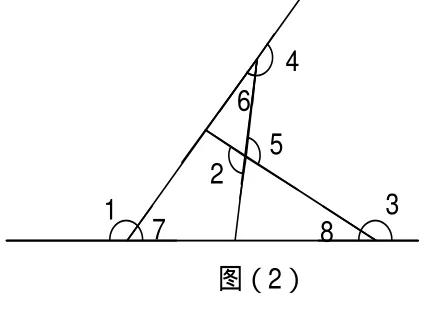
例1.如图（2）求∠1+∠2+∠3+∠4的度数。

略解：由“A”字形可知∠2=∠5=∠6+∠7+∠8，而易发现∠6+∠4=180°①；∠1 +∠7=180°②；∠3+∠8=180°③；然后①+②+③便可知∠1+∠2+∠3+∠4=540°，由此可见抓住模型解决问题非常简单。学生学习几何不再困惑，而是感到很有趣，遇到问题不会再束手无策。

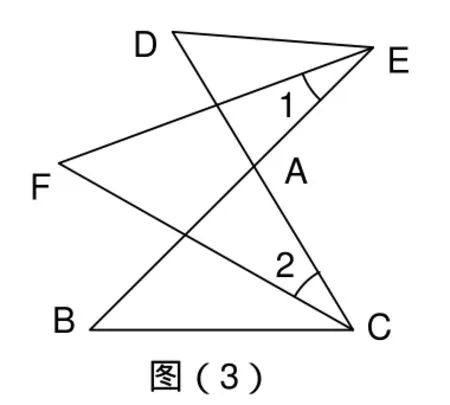
例2.如图（3）BE与CD相交于点A，CF为∠BCD的平分线，EF为∠BED的平分线，

（1）试探求∠B、∠D、∠F之间存在何种数量关系？

（2）若∠B:∠D:∠F=2:4:a,求a的值

略解：（1）∵∠EAC=∠1+∠2+∠F,

（2）由（1）的结论便可求解。略解：∵∠B:∠D:∠F=2:4:a，

∠B+∠D=2∠F，∴2a=6, ∴a=3

利用此模型也可解决很多问题，如后面的例3以及练习1都可以用此模型来解。用此模型解就是∠BOC=∠A+∠B+∠C,而∠BOC=∠EOF,所求的五个角的和就化归到△EOF中了。而练习1用模型解就是∠DOC=∠A+∠D+∠C=∠BOE,所求的五个角的和就化归到△BOE中了。显而易见，学生掌握模型、抓住模型的特点对学生解题是非常有利的，这样不仅解决了问题，同时又拓宽了学生的解题思路，培养了学生灵活解决问题的能力。

问题引入（二）：初一几何中有这样一道简单的求角的度数的问题，如图（4）已知∠A=40°，∠D=60°，∠C=30°求∠B的度数。

其基本解法有两种：一种是先求出∠AOD的度数，然后利用对顶角相等这一原理求出∠BOC的度数，再利用三角形的内角和180°便可求出∠B=70°；另一种方法是由三角形的内角和180度，可得∠A+∠D=∠B+∠C，便可求出∠B=70°，方法很巧妙，思路很简捷。由此发现只要是这种模型——“8”字形就一定存在这一结论，而且在教学中发现这样的问题很多见，有的是小题，有的是在证明题中会间接应用它，用它可以很快捷的解决很多问题。

构建模型：具有上述图形特点的问题都可用其原理求解，由于图形象“8”字，就称其为“8”字形，只要具备这一模型特征，就可以用它快捷的解决问题，思维简单明了，学生运用起来也灵活自如，在教学中应用此法，学生们的思路、速度快了很多。

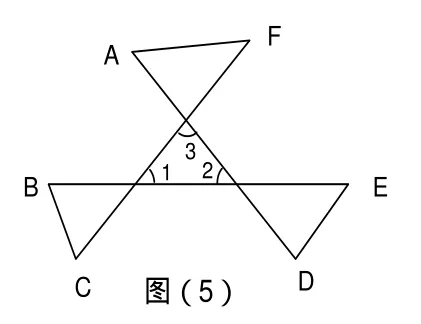
具体应用如例3：如图（5）求∠A+∠B+∠C+∠D+∠E+∠F的度数。

很容易发现此题属于典型的“8”字型问题，题中蕴含了三个“8”字形，用“8”字形的结论便可得:①∠A+∠F=∠1+∠2;②∠B+∠C=∠2+∠3; ③∠E+∠D=∠1+∠3; 将①、②、③相加便可得∠A+∠B+∠C+∠D+∠E+∠F=2（∠1+∠2+∠3）=360°.发现用此种方法解题思路特别顺畅。

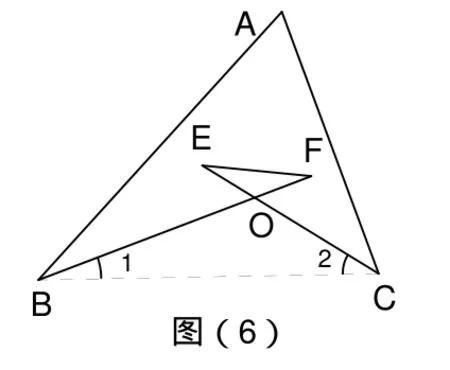
例3.如图（6）计算∠A+∠B+∠C+∠E+∠F的度数。

观察中发现此题很象“8”字形，但还差一点，只要连接BC便可得到“8”字形，因此想到了作辅助线的方法——连接 BC,则有∠E+∠F=∠1+∠2，所以∠A+∠B+∠C+∠E+∠F=∠A+∠B+∠C+∠1+∠2=180°，将这 5个角化归到同一个三角形中问题得以解决。

以下是一组练习：1.如图（7）求∠A+∠B+∠C+∠D+∠E的度数。

提示：连接图中任意相邻两点便可构成“8”字形，很容易的将这5个角化归到同一个三角形中，使问题得已解决。（如连接 CD,则∠E+∠B=∠1+∠2, ∴∠A+∠B+∠C+∠E+∠F=180°）

2.如图（8）求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数。

提示：连接NQ便可得两个“8”字形；再连接 MR又可得两个“8”字形，便将所求的8个角全部归到四边形MQRN中，利用四边形的内角和便可求得。

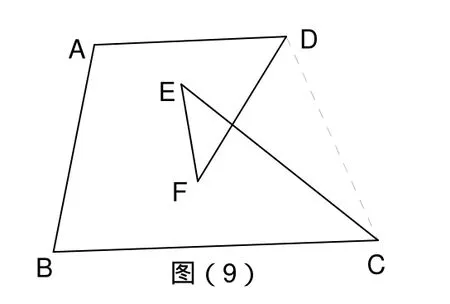
3.如图（9）求∠A+∠B+∠C+∠D+∠E+∠F的度数

提示：连接CD就可构造出模型，利用模型就很容易的将这六个角化归到四边形ABCD中，利用四边形的内角和求得；六个角的和为360°。

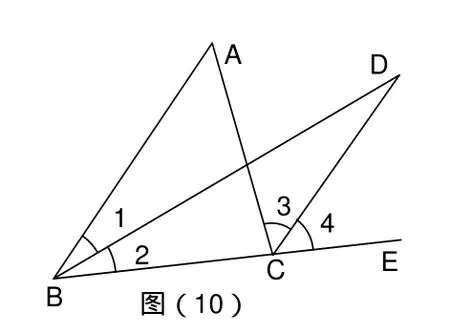
“8”字形也可用在证明题中。如图（10），已知BD为∠ABC的平分线，CD为⊿ABC的外角∠ACE的平分线，CD与BD交于点D，试说明∠A=2∠D.

分析：图中很明显有“8”字形，利用其原理可得∠A+∠1=∠D+∠3;又由内外角关系可得∠4=∠D+∠2，而BD为∠ABC的平分线可得∠1=∠2，CD为⊿ABC的外角平分线可得∠3=∠4；所以∠A+∠1=∠2 +∠D +∠D；所以∠A=2∠D

“8”字形不仅仅在求角的计算问题中出现，而且在解“相似三角形”问题时也会用到。

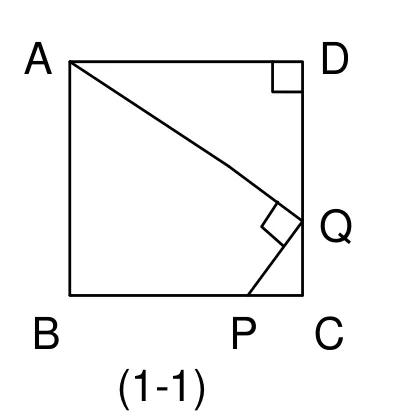
引例：如图(1-1)，正方形ABCD中，P是BC上一点，Q是CD上一点，且AQ⊥P Q,求证; △ADQ∽△QCP.

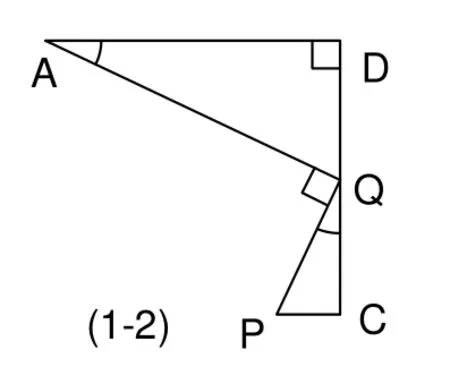
分析：由正方形和AQ⊥PQ不难证出∠DAQ=∠PQC,再加上∠D=∠C就可证出△ADQ∽△QC P.因此，只要有三个垂直就可得到两个三角形相似。若图形中只要两个三角形，就会发现这个图形也象“8”字形如图（1-2），而且这个模型在相似形这部分应用非常广泛，无论是计算还是证明或者实际应用问题都会用到它，因此，掌握这一模型对我们今后解决问题会有很大帮助。

比如：1.运用这一模型可以求线段的长度。如图（1-3），在梯形 ABCD中，AB∥DC,∠B=90°，E为BC上一点，且AE⊥ED,BC=12，DC=7，BE:EC=1：3，求AB的长。

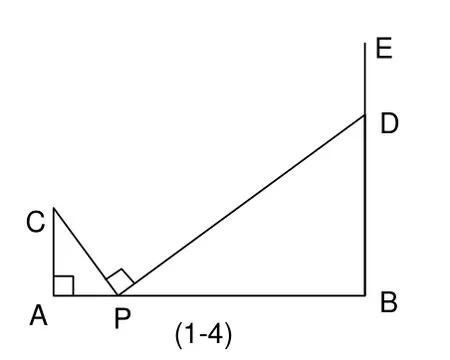
2.实际操作问题：如图（1-4），A C⊥AB,BE⊥AB,AB=1 0，AC=2，用三角板进行如下操作：将直角顶点P在线段AB上滑动，直角边始终经过C点，另一条直角边与BE相交于点D，且BD=8，求AP的长。

分析：将直角三角板的直角顶点P在线段AB上滑动就会出现1题的情况，即与模型相似。因此解法与1题解法类似，解出之后满足条件的点P有两个。

3.变式题——解决动点问题：如图（1-5），已知AB⊥BC 于 B,CD⊥BC于 C,AB=4，CD=6，BC=14，P为BC上一点。则BP为何值时，△ABP与△PCD相似？

分析：不难发现，此题与前两题类似,唯一不同的就是有两种情况（1）△ABP∽△PCD，（2）△ABP∽△DCP.即当∠A=∠DPC时满足（1）的情况，此时AP⊥PD;当∠A=∠D时满足（2）的情况。此时AP不垂直于PD。解出后满足条件的点P有三个。

略解：∵AB⊥BC,DC⊥BC, ∴∠B=∠C=90°,

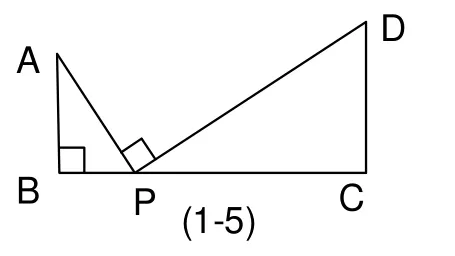
4.实际应用。如图(1-6)，某同学要测量某烟囱的高度，他将一面镜子放到地面上某一位置，然后站到与镜面、烟囱成一直线的地方，刚好看到烟囱顶部的像。如果这名同学的眼睛到地面的距离AB=1.6m，他到镜面的距离BO为2m，测得镜面到烟囱的距离OD为30m，求烟囱的高度。

分析；将本题的实际问题抽象出几何图形如图所示，不难发现，其实本题运用的基本原理就是模型中的原理，所不同的是由于放在地面上的是平面镜，所以利用入射角等于反射角这一原理就可以得出∠AOB=∠DOC,再加上两个直角，就可得到两个三角形相似。利用对应边成比例就可直接求出烟囱的高度。

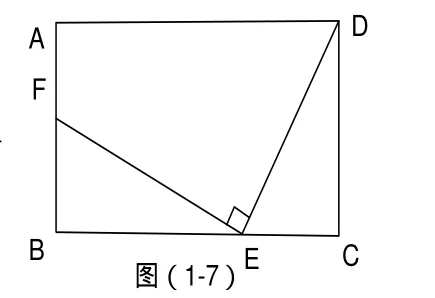
5.利用模型求函数的解析式。如图（1-7）在矩形ABCD中，AB=m（m是大于0的常数），BC=8,点E为线段BC上的动点（不与B、C重合），连接 DE,作EF⊥DE,EF与射线BA交于点F，设CE=x,BF=y.(1)求y关于x的函数关系式；(2)若m=8,求x为何值时，y的值最大，最大值是多少？

从以上的问题可以看出，只要具备这两个特点——“8”字形、“A”字形的问题，就都可以用它们的模型来解决问题，而且抓住模型特点，学生在解决问题时思路非常快捷。