区间集上R0-代数的表示形式及其性质*

乔希民，张东翰

(商洛学院数学与计算机应用学院，陕西商洛726000)

自美国模糊控制专家Zadeh于1965年发表模糊集理论［1］以来，模糊集理论上的模糊逻辑就成为一种非古典、非标准的现代逻辑，即形成了现代逻辑科学中以模糊逻辑为主要研究对象的非经典数理逻辑学［2］，而这种非经典数理逻辑学完备性问题的讨论，则可归结为其相应代数系统的完备性研究.比如，Chang于1958年为研究Łukasiewicz逻辑系统所建立的MV-代数理论［3，4］;1996年，捷克逻辑学家Hájek提出了与基本逻辑系统BL相对应的BL-代数及其虑子理论［5］;而我国数学家王国俊教授则提出了一种新的模糊命题演算的形式系统L*［6，7］，继而经多次修改趋于完善的L*系统，被视为是一种基于R0型t-模及其剩余蕴涵R0蕴涵算子，即为证明模糊逻辑形式系统L*的完备性而建立了与之相匹配的R0-代数系统［2，8］.此处拟在国内外诸多学者对区间集［9-12］与相关R0-代数理论系统［13-16］研究的基础上，运用其基本思想方法，构造性地给出了区间集上R0-代数的表示形式，同时证明了区间集上R0-代数定义表示形式的可行性与合理性，最后讨论了其有趣的基本性质.

1 基本概念

定义1［9-12］设A=［Al，Au］是一个区间集，其中Al，Au是任意经典集合且Al⊆Au.区间集是用上、下界集合对来表示，且其定义如下:设U为论域，2U是U的幂集，那么区间集上2U的子集形式为A=［Al，Au］={A∈2U|Al⊆A⊆Au}，称其为一个闭区间集.闭区间上的所有区间集的集合记为 I(2U)={［Al，Au］|Al，Au⊆U，Al⊆Au}.

注1 当 Al=Au时，区间集 A=［Al，Au］成为经典集合 A，尤其全集 U=［U，U］，空集∅ =［∅，∅］.

定义2［9-12］设A，B是任意的区间集，则在I(2U)上定义如下:

A⊆B 当且仅当 Al⊆Bl和 Au⊆Bu.

定理1 设A，B，C∈I(2U)，则下列各结论成立:

(1)∅⊆A⊆U(有界性);

(2)A⊆A(自反性);

(3)A⊆B，B⊆A⇒A=B(反对称性);

(4)A⊆B，B⊆C⇒A⊆C(传递性).

这样由定理1中的(2)(3)(4)易知“⊆”是I(2U)上的一种偏序关系，带偏序的区间集集合〈I(2U)，⊆〉为偏序集.

2 区间集间的运算与性质

定义3［9-13］设A，B是任意的区间集，那么区间集上的交、并、补、伪补与蕴涵规定为

(1)A∩B≜［Al∩Bl，Au∩Bu］，称为区间集 A 与 B 的交集;

(2)A∪≜B［Al∪Bl，Au∪Bu］，称为区间集 A 与 B 的并集;

(3)A'≜［U-Au，U-Al］，称为区间集 A 的补集或余集;

(4)A*≜［U-Al，U-Al］，称为区间集 A 的伪补集;

(5)A⇒B≜A'∪B∪(A*∩(B')*)，称为区间集A蕴涵区间集B，简称蕴涵区间集.

其中符号“≜”表示“被定义为”.

注2 A'与A*是两种完全不同的定义方式.

定理2 设 A，B，C∈I(2U)，则

(1)幂等律 A∪A=A，A∩A=A;

(2)交换律A∪B=B∪A，A∩B=B∩A;

(3)结合律 (A∪B)∪C=A∪(B∪C)，(A∩B)∩C=A∩(B∩C);

(4)分配律 A∪(B∩C)=(A∩B)∪(A∪C)，A∪(B∩C)=(A∪B)∩(A∪C);

(5)吸收律 (A∩B)∪A=A，(A∪)∩A=A;

(6)同一律 A∪U=U，A∩U=A，A∪∅ =A，A∪∅ =∅;

(7)排中律 A∪A'=U，A∪A'=∅;

(8)De Morgan对偶律

(ⅰ)区间补对偶律(A∩B)'=A'∪B'，(A∩B)'=A'∩B';

(ⅱ)区间伪补对偶律(A∩B)*=A*∩B*，(A∪B)*=A*∩B*.

该定理的证明只需直接利用定义3，同时注意到经典集合运算的性质即可.

注3 上述两个区间集的并、交运算可推广到任意多个区间集的并、交运算.

定理3［9-12］设A，B是任意的区间集，则区间集的补A'，B'和区间集伪补A*，B*之间的多重否定与多重伪补及混合运算，具有下列性质:

(1)A'⊆A*，A＊＊⊆A'*;

(2)A″=A，A‴=A';

(3)A'*=［Au，Au］，A*'=A＊＊=［Al，Al］;

(4)A'*'*=A'*=［Au，Au］;

(5)A'*'=A'＊＊=［U-Au，U-Au］;

(6)A″*=A*'*=A＊＊＊=A＊＊'=A*''=A*;

(7)A'∪A*=A*，A'∩A*=A';

(8)A∪A*=U，A∩A*=∅.

证明 直接根据定义3证得.

定理4［9-12］设A，B是任意的区间集，则区间集补和区间集伪补所满足的对偶性质有:

(A∩B)'*=A'*∪B'*;(A∪B)'*=A'*∩B'*;(A∩B)*'=A*'∪B*';(A∪)B*'=A*'∩B*'.

证明 由定理2中的(8)证得.

定理5［9-12］如果'是I(2U)→I(2U)的一个自身逆序对合映射，即

(1)A⊆B当且仅当B'⊆A'('是逆序对应);

(2)A″=A('是对合对应).

则称格〈I(2U)，B，B，'，*〉为有余格.

3 区间集上R0-代数的表示形式

为方便起见，由定义1、定理2、定理3还可将区间蕴涵表示为

命题1［13］设A，B是任意的区间集，“'”为区间集上的补，“⇒”为区间集的蕴涵，则

(1)A⇒B=［(U-Au)∪Bl∪((U-Al)∩Bu)，(U-Al)∪Bu］;

(2)A⇒B=［((U-Al)∪Bl)∩((U-Au)∪Bu)，(U-Al)∪Bu］;

(3)A'⇒B=［Al∪Bl∪(Au∩Bu)，Au∪Bu］，记 A△B≜A'⇒B;

(4)(A⇒B')'=［Al∩Bl，Au∩Bu∩(Al∪Bl)］=(A'△B')'，记 A⊗B≜(A'△B')'=(A'⇒B')'.

命题2 设X，Y，Z是任意的区间集，则⇒:I(2U)×I(2U)→I(2U)是一映射，“⊆”是I(2U)上的偏序，U是I(2U)上的有界最大元，“'”是关于序⊆逆序对合对应，且满足以下性质:

(1)X'⇒Y'=Y⇒X;

(2)U⇒X=X，X⇒X=U;

(3)Y⇒Z⊆(X⇒Y)⇒(X⇒Z);

(4)X⇒(Y⇒Z)=Y⇒(X⇒Z);

(5)X⇒(Y∪Z)=(X⇒Y)∪(X⇒Z)，X⇒(Y∪Z)=(X⇒Y)∪(X⇒Z);

(6)(X⇒Y)∪((X⇒Y)⇒(X'∪Y))=U.

证明 (1)由区间集蕴涵定义及定理2、定理3得

X'⇒Y'=X″∪Y'∪(X'*∩Y″*)=X∪Y'∪(X'*∩Y*)=Y'∪X∪(Y*∩X'*)=Y⇒X

故证得(1)成立.

(2)根据区间集蕴涵的区间表示式，得

U⇒X= ［(U-U)∪Xl∪((U-U)∩Xu)，(U-U)∪Xu］=［Xl，Xu］=X

X⇒X=［((U-Xl)∪Xl)∩((U-Xu)∪Xu)，(U-Xl)∪Xu］=［U，U］=U故证得(2)成立.

(3)依区间集蕴涵的意义得

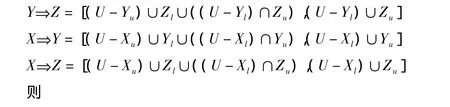
从而证得(3)成立.

(4)利用区间集蕴涵的意义与定理2，3，4得:

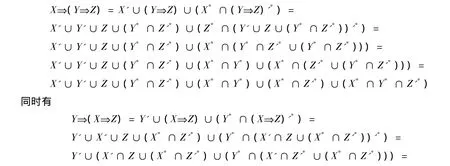
故证得(5)成立.

(6)由区间集蕴涵、补及并的定义有

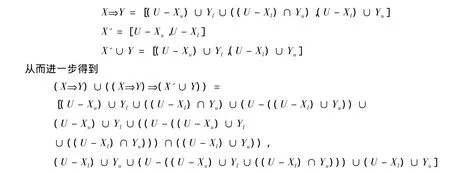
因为区间集较为冗长，所以分别计算证明其上确界值和下确界值.

在区间集上确界值中，利用经典集合排中律及幂等律得

故证得(6)成立.

注4 在命题2中，式(1)-(6)均可用定义3及命题1证得.

这样，受文献［2，8］的启发，给出区间集上R0-代数的定义如下:

定义4 设 X，Y，Z 是任意的区间集，一个(2，2，2，1，1，0，0)型代数〈I(2U)，⇒，⊆，∪，'，*，U，∅〉是区间集上R0-代数，若以下条件成立:

4 区间集上R0-代数的性质

命题3 设〈I(2U)，⇒，⊆，∪，'，*，U，∅〉是区间集上R0-代数，X，Y，Z是任意的区间集，则以下性质成立:

(P1)X⇒Y=U当且仅当X⊆Y当且仅当Y'⊆X';

(P2)X⊆Y时，有Y⇒Z⊆X⇒Z即X⇒Y关于X不增，继而由此得到X⇒Y=U，另外特别地有Y'⊆X';

(P3)X⊆(X⇒Y)⇒Y;

(P4)X⊆Y⇒Z当且仅当Y⊆X⇒Z;

(P5)(X∪Y)⇒Z=(X⇒Z)∩(Y⇒Z)，(X∩Y)⇒Z=(X⇒Z)∪(Y⇒Z);

(P6)(X⇒Y)∪(Y⇒X)=U;

(P7)X∪X'⊆Y∪Y';

(P8)X⇒(X'⇒Y)=U;

(P9)X⇒(Y⇒X)=U;

(P10)X∪Y⊆((X⇒Y)⇒Y)∩((Y⇒X)⇒X);

(P11)X⇒Y⊆(X∪Z)⇒(Y∪Z)，X⇒Y⊆(X∪Z)⇒(Y∩Z);

(P12)X⇒Y⊆(X⇒Z)∪(Z⇒Y).

命题4 设〈I(2U)，⇒，⊆，∪，'，*，U，∅〉是区间集上R0-代数，X，Y，Z是任意的区间集，利用命题1中的(3)(4)所引入的两个新的算子“Δ”与“⊗”，则以下性质成立:

(P13)X⊗Y⊆X∩Y⊆X∪Y⊆X△Y;

(P14)X⊗Y⊆Z当且仅当X⊆Y⇒Z;

(P15)(X⊗Y)⇒Z=X⇒(Y⇒Z)，X⇒(Y⇒(X⊗Y))=U;

(P16)X⊗X'=∅，X△X'=U;

(P17)nX=2X，Xn=X2，这里n是大于2的整数，nX=X△X△…△X，(X)n=X⊗X⊗…⊗X(以上各式均有n个X);

(P18)X⊗(Y∪Z)=(X⊗Y)∪(X⊗Z);X⊗(Y∩Z)=(X⊗Y)∩(X⊗Z)

(P19)(X∪Y)n=Xn∪Yn;

(P20)X2⇒(Y⇒Z)=(X2⇒Y)⇒(X2⇒Z).

5 结束语

此处是基于区间集上R0-代数及其性质的讨论，对此区间集上R0-代数的定义是否可以进一步简化，具有哪些特征刻画，以及如何在区间集上建立相应的模糊逻辑形式系统ISL*等问题的研究，都将是另文所要深入探讨的课题.

［1］LOTFI A，ZADEN.Fuzzy Sets［J］.Information and Control，1965，8(3):338-353

［2］王国俊.非经典数理逻辑与近似推理［M］.2版.北京:科学出版社，2008

［3］CHANG C C.Algebacic Analysis of Many-valued Logics［J］.Transations of the Aemerican Mathematical Society，1958，88:467-490

［4］CHANG CC.A New Proof of the Completeness of the Lukasiewicz Axioms［J］.Transations of the American Mathematical Society，1959(93):74-90

［5］HÁJEK P.Metamathematics of Fuzzy Logic［M］.Boston:Kluwer Academic Publishers，1998

［6］王国俊.模糊命题演算的一种形式演绎系统［J］.科学通报，1997，42(10):1041-1045

［7］WANG G J.On the logic foundation of fuzzy reasoning［J］.Information Sciences，1999，177(1):47-88

［8］WANG G J，AHOU H J.Introduction to Mathematical logic and Resolution Principle［M］.2nd ed.Beijing:Science Press，2009

［9］YAO Y Y.Interval Sets and Interval-set Algebras［C］∥The 8th IEEE International Conference on Cognitive informatics.Hong Kong:IEEE Computer Society，2009:307-314

［10］姚一豫.区间集［M］∥王国胤，李德毅，姚一豫，等.云模型与粒计算.北京:科学出版社，2012

［11］YAO Y Y.Two Views of Theory of Rough Setsin Finite Universes［J］.International Journal of Approximation Rersoning，1996，15(4):291-317

［12］薛战熬，杜浩翠，尹昊喆，等.区间集上的格蕴涵代数、FI-代数、MV-代数的研究［J］.计算机科学，2010，37(12):218-223

［13］裴道武.基于三角模的模糊逻辑理论及其应用［M］.北京:科学出版社，2013

［14］张小红.模糊逻辑及其代数分析［M］.北京:科学出版社，2008

［15］乔希民，吴洪博.格上BR0-代数结构的表示定理［J］.山东大学学报:理学版，2010，45(9):38-42

［16］乔希民，吴洪博，罗俊丽.16种基础R0-代数结构的相对独立公理系统［J］.模糊系统与数学，2012，26(6):14-20