非均匀泵浦的半经典自洽场激光理论
刘勇,祁红艳,刘劲松,王可嘉
(1.湖北第二师范学院物理与电子信息学院,湖北 武 汉430205;
2.武汉光电国家实验室,华中科技大学光电子科学与工程学院,湖北 武 汉430074)
0 引言
激光是重要的非线性系统,在泵浦域值之上,这种系统能够产生一束干涉光,其频率从红外至紫外且低发散.由于当代纳米制造能力的快速发展,一系列新颖的激光系统已经出现.例如,垂直腔面发射激光器(VCSEL)[1]、光子晶体缺陷模激光(Phcs)[2]和随机激光器(RLs)[3~5].这一系列激光器所面临的理论挑战是对开腔的正确处理.在传统理论中,多模激光是用线性腔共振来描述的,其中一种较常用的处理方式是准态模(QB)[6].尽管准态模(QB)已广泛使用于标准的开腔分析,但是由于它们彼此不正交,所以使用准态模(QB)在增益区外光子流通量不守恒,而且这种方法不能处理模式相互作用及空间烧孔.近来,这些困难已由Hakan E Türeci和A Douglas Stone等人引入常通量模式constant flux(CF)态所克服[7],这种CF态所决定的光子流通量守恒.他们从采取旋转波近似以及缓慢包络近似的半经典激光方程出发,推导出了一个迭代可解的自洽积分方程,这个方程决定了激光谐振腔内的稳态激光模式.在这个模型中,半导体激光谐振腔有均匀的折射率和泵浦.
当泵浦区域(或折射率)不均匀时,必须对常通量模式作进一步处理.本文中扩展了自洽积分方程的适用范围,并扩展到一维边缘发光半导体激光器,分析了第一激光域值随着泵浦区域的变化趋势.计算结果显示,第一激光域值D(1)th与泵浦区域x0成反比.这种处理方式能够进一步应用于更复杂的谐振腔.
1 理论模型
Hakan E Türeci等人[7]从 Maxwell-Bloch方程出发,给出电场的多周期形式E(x,t)= ∑μψμ(x)e-ikμt,稳态非线性激光模式能够由常通量CF态的复矢量aμ方程得到:
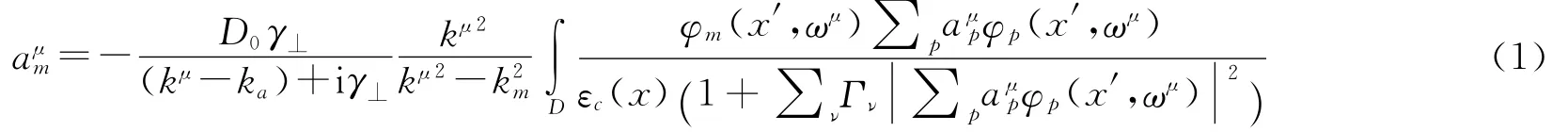
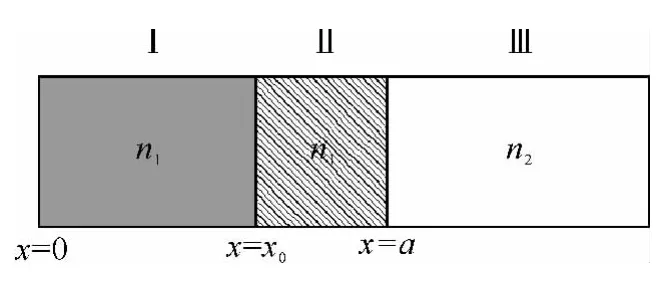
图1 仅有层Ⅰ为增益的一维边缘发光半导体激光谐振腔
为了处理不均匀泵浦时的常通量模式,忽略在未泵浦区域增益介质光子的重吸收.如图1,半导体谐振腔分为两层:层Ⅰ和层Ⅱ,它们分别是泵浦(x<x0)和未泵浦区域(x>x0),且层Ⅰ是持续泵浦的.腔的外部标注为层Ⅲ,为空气(n2=1).腔的左部(x=0)处是一面全反射镜.
腔内的CF态由下列方程决定:
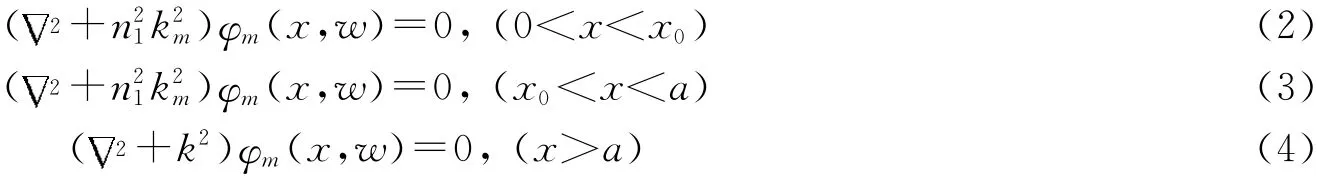
在x=0处,考虑Dirichlet边界条件.在x=a处,考虑辐射波边界条件(∂xφm(x=a)=ikφm(x=a)),(2)~(4)式决定的CF态经过简单地计算可得出:
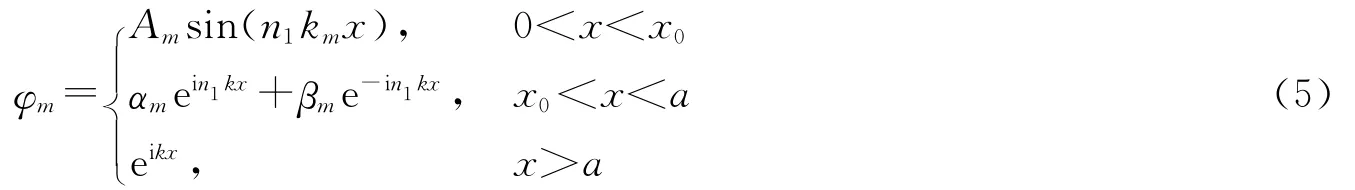
这里,层Ⅱ中波矢k选择为实数并恒定,因为层Ⅱ中增益介质并没有泵浦,所以激光模式无法放大.又由φm在x=x0及x=a处连续性条件,可以推得层Ⅰ中CF态频率km满足下列方程:
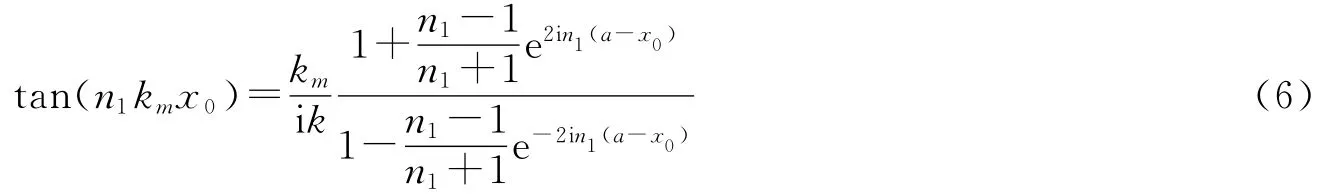
为了简化公式,定义

则(6)式简化为

这样(8)式和参考文献[5]中的公式有了相同的形式,在域值上,k标注为kμth.为了求出CF态的系数,对(5)式在x=x0及x=a引入Dirchlet条件,推得
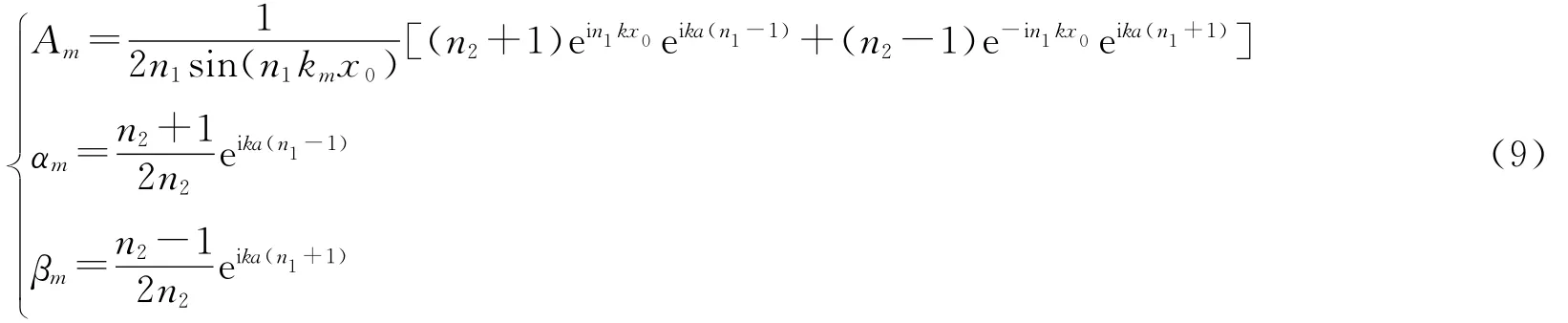
(1)式化为:
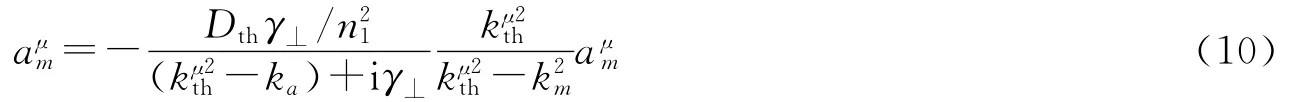
为了解(10)式,必须应用全局相位条件.通常取的系数是实数且为1.第一域值频率及第一泵浦域值为:


上式中,

联立(8)式、(11)式和(13)式,即可得解得第一域值频率和km,再由式(12)求得第一泵浦域值
2 模拟与讨论
首先,计算第一域值与泵浦区域的关系.假设腔外的稳定波矢K=20,分别取泵浦区域x0=0.3,0.5,0.7,0.9,使用(8)式计算CF态的频率,在计算中取m=9,然后代入(9)式得到CF模式系数,从而计算出CF态φm,作出图2,计算参数与参考文献[8]中的一致,如下:a=1,ka=19.89,n1=1.5,n2=1.0,γ⊥=4.从图2可以看出,边界x=a处强度相等,这时CF态放大率明显不同.经过仔细考察,层Ⅰ的放大率与增益区域x0(即泵浦区域)成反比,这说明随着增益区域x0的减小,需要更高的泵浦补偿未泵浦腔长(a-x0)的损耗.在腔外,强度为常数,这是由于光子流通量守恒,也是CF态理论与传统的准态模理论的根本区别.
如图3,改变泵浦区域x0,分别计算第一泵浦域值.随着泵浦区域x0的增大,泵浦域值减小,即第一泵浦域值与泵浦区域x0成反比.
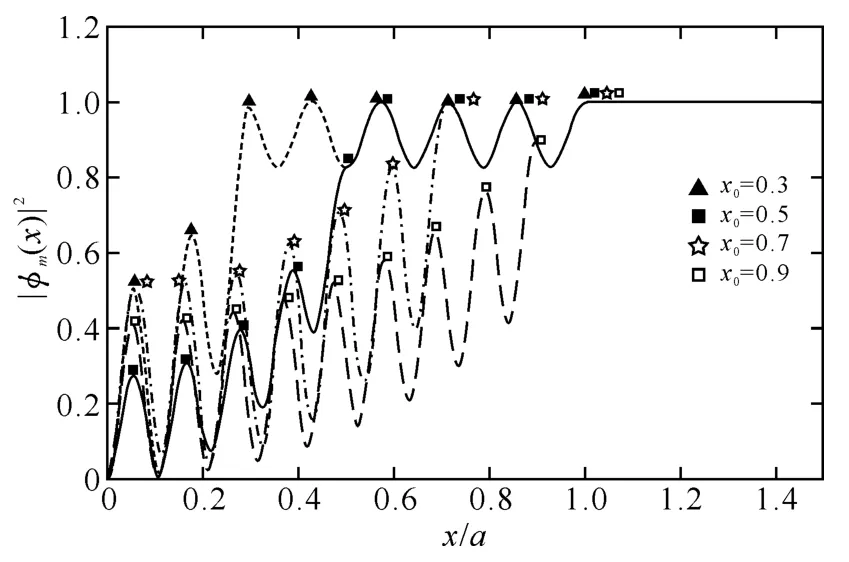
图2 边缘发光腔中计算的一系列增益区域CF态分布
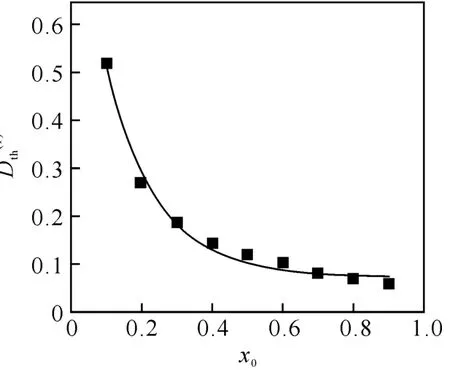
图3 第一泵浦域值随泵浦区域x0的变化规律
3 结 论
将半经典自洽场激光理论由均匀泵浦扩展到不均匀泵浦,并以一维半导体边缘发光为例,详细阐述了我们的计算策略,希望这种新的理论能够应用到解决复杂结构以及随机激光的增益阈值的求解.
[1]Fumio Koyama.Recent advances of VCSEL photonics[J].J Lightwave Technol,2006,24(1):4502-4513.
[2]Noda S,Chutinan A,MImada.Trapping and emission of photons by a single defect in a photonic bandgap structure[J].Nature,2000,407(5):608-610.
[3]Lawandy N W,Balachandran R M,Gomes A S L,et al.Laser action in strongly scattering media[J].Nature,1994,368(6470):436-438.
[4]Sun T,Wong K S.Time-resolved study of the random lasing in ZnO powder[J].Acta Phys Sin,2003,52(9):2127-2132.
[5]Liu J S,Wang H.Influence of spatial localization on the threshold of quasi-state cavities in random lasers[J].Acta Phys Sin,2004,53(12):4224-4228.
[6]Wiersig J,Hentshcel M.Combining directinal light output and ultralow loss in deformed microdisks[J].Phys Rev Lett,2008,100(3):033901-033904.
[7]H Türeci E,Stone A D,Collier B.Steady-state ab initio laser theory:generalizations and analytic results[J].Phys Rev A,2006,74(4):043822-043838.

