基于一类负相依市场下的log－最优资产组合模型

黄敏，黄朝炎

（1．中南财经政法大学武汉学院信息系，湖北 武 汉430079；2．湖北大学数学与统计学学院，湖北 武 汉430062）

0 引言

现代证券组合理论（modern portfolio theory）是关于在收益不确定条件下投资行为的理论，它是由美国经济学家Harry Markowits在20世纪50年代提出来的．文献［1－2］研究了市场不允许卖空及市场为独立情形下log－最优资产组合的问题．但是，实际的经济生活中证券市场存在大量的卖空操作，市场也通常不独立，因此对市场不独立情形的研究无疑是非常重要的．本文中研究了允许卖空的离散时间金融市场，从无风险控制和有风险控制两个方面探讨允许卖空的log－最优资产组合投资问题，当市场满足一类负相依随机变量序列条件下，得到关于log－最优资产组合的一些性质．

1 无风险控制条件下log－最优资产组合的性质

先考虑单周期情形．设（Ω，F，P）是其构成的概率空间，其中Ω表示证券收益所有可能状态．记ω＝（ω1，ω2，…，ωm）T为资产组合向量．这里ωi，i＝1，2，…，m 可以大于等于0也可以小于0．在文献［1］中，假设ωi≥0，不允许卖空，但现实的证券市场中卖空的操作大量存在，所以考虑ωi＜0，即表明允许卖空的情形．

记X＝（X1，X2，…，Xm）T为收益向量，T表示转置，其中Xi表示把单位资金投资于第i种证券，经一定时间后得到的收益．X 的联合分布函数记为F（x）．记B＝｛ω∈Rm｜eTω＝1，ωTX＞0，e＝（1，1，…，1）T｝为全体资产组合向量集．对数是一种常用效用函数，在多周期情形中为了在数学上便于处理，我们对累计资金ωTX 求 取对数，令为倍率函数．投资者是厌恶风险者，所以投资者目标是使倍率函数W（ω，X）达到最大值，称）为最优倍率函数．对于单周期允许卖空的市场，最优倍率函数有如下性质．

引理1［1］对于给定的ω，W（ω，X）是F（x）的线性函数．对于给定的F（x），W（ω，X）是ω的凹函数．

W＊（X）是F（x）的凸函数．

引理2［2］使倍率函数W（ω，X）达到最大的log－最优资产组合ω＊冰满足条件

再考虑多周期情形．由于投资者实际上是连续投资，设n为一个有限时间，所有到n时刻为止的市场不确定性形成概率空间（Ω，F，P），并在其上形成一个σ－域流Fk，Fk＝σ（Xi，i≤k），且F1⊆F2⊆…⊆Fn⊆F．

令ω＝（ω ，ω ，…，ω ）T为投资者第i个周期的资产组合向量．X＝（X，X，…，X）T为收益向量，则到第几个周期末投资者拥有的资金累计为），相应的log－收益为为第i个周期的log－收益，即记为第i个周期达到的log－最优资产组合即

引理3［3］设｛Xn，n≥1｝是随机变量序列，｛an，n≥1｝是正实数列且an↑∞（n→∞）．若其满足下列条件

则强大数定律

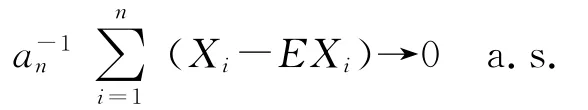
成立．

定理1 设｛Xn，n≥1｝为市场收益向量序列，记为第i个周期的log－收益，若它是一类负相依序列，即

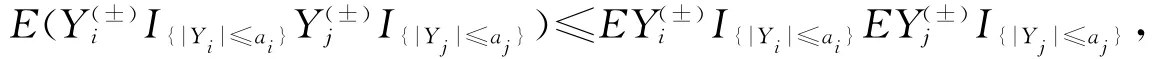
其中i≠j，i，j＝1，2，…，则

定理1的证明 由条件知

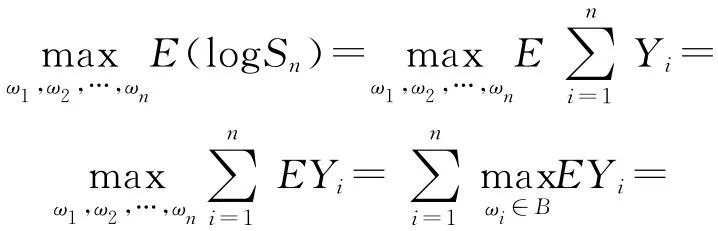
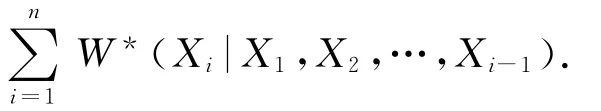
又

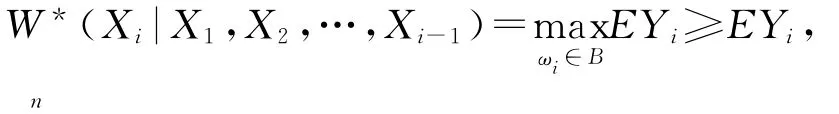
定理2 设｛Xn，n≥1｝为收益向量序列，记）为第i个周期达到log－最优组合投资的log－收益，若它是一类负相依序列，即

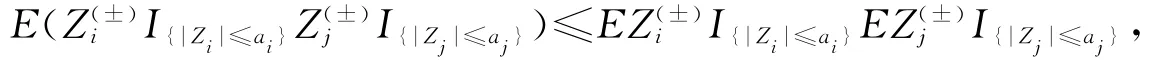
其中i≠j，i，j＝1，2，…．而Zi满足

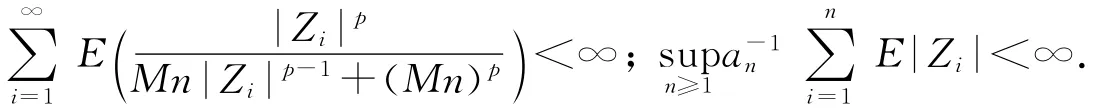
定理2的证明 由于｛Zn，n≥1｝满足条件

其中i≠j，i，j＝1，2，…．由引理3知

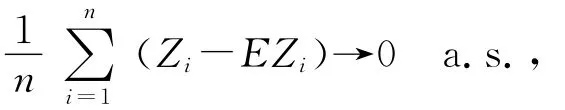
即

由定理1有

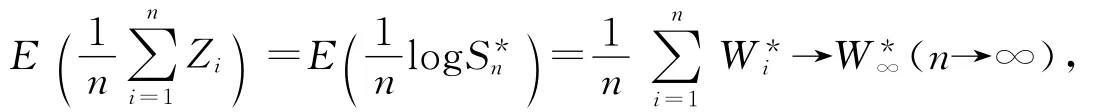
故

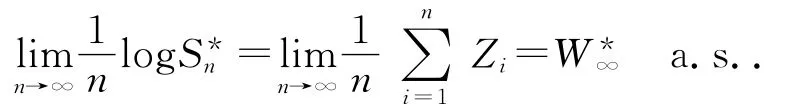
于是（1）式成立．

又由引理2知，对每个周期有

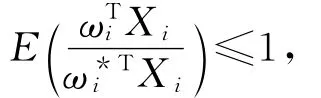
于是

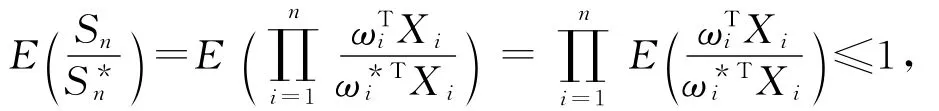
利用Markov不等式可得

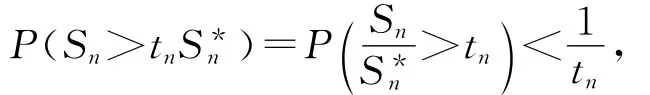
从而

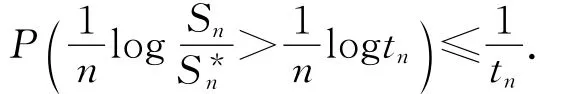
取tn＝n2，并对n求和得

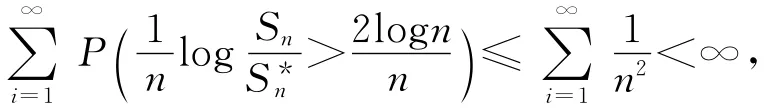
则由Borel－Cantelli引理有

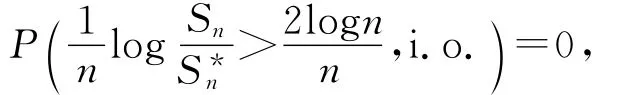
即存存N，当n＞N时．有

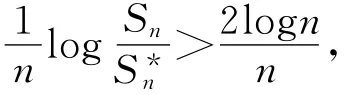
从而有

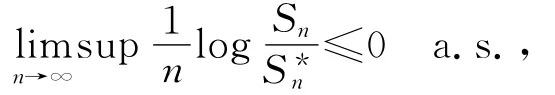
即（2）式成立．

3 有风险控制条件下log－最优资产组合的性质

上面我们讨论了在无风险控制条件下log－最优资产组合的问题，但在实际投资策略中，风险是必然存在的，所以我们必须考虑如何规避风险、考虑对风险的承受程度，在风险不超过一定程度下寻求投资效益的最大化，或者在收益不低于一定程度时寻求投资风险的最小化．在投资活动中风险是投资决策的实际结局可能偏离其期望结局的程度，收益的方差或标准差、半方差是用于风险度量的最常用的讨论．为此，下面我们将用更一般的数学度量来讨论有风险控制条件下log－最优资产组合的问题．

设‖·‖为R的凸函数，定义风险控制函数为R（ω）＝E‖ωTX－E（ωTX）‖．记投资风险不超过r的投资组合的全体为Br＝｛ωr∈B：R（ωr）≤r｝．为了刻划在风险水平不超过r的资产组合中能达到的log－最优投资收益，令

为最优倍率－风险函数．

当r＝∞时，W＊（∞，F）＝W＊（F），此时最优倍率－风险函数即为上节中的最优倍率函数W＊（F）．若最优资产组合记为，则W＊，F）＝W＊（r，F）．

在单周期情形中，类似于上一节无风险的情形，我们有如下结论：

引理3［1］倍率函数W（ωr）是ωr的凹函数．

引理4［2］达到log－优倍率－风险函数的资产组合ωr＊满足条件：

在多周期情形中，定义第i个周期投资的资产组合的最优倍率－风险函数为，到第n个周期末为），其中最大值满足如下集合

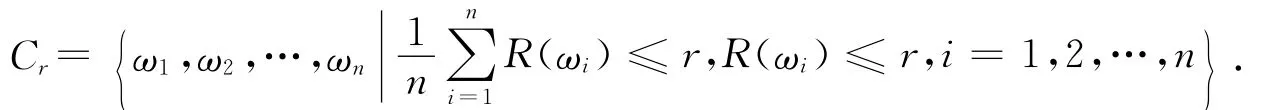
定理3 设｛Xn，n≥1｝为市场收益向量序列，记Yi＝log（ωtiXi）为第i个周期的log－收益，若它是一类负相依序列，即

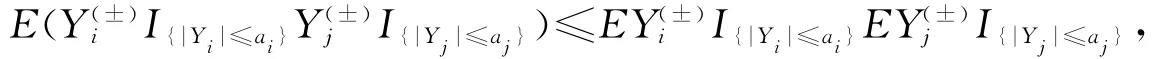
其中i≠j，i，j＝1，2，…．则

定理3的证明 根据集合Cr的限制可得如下不等式

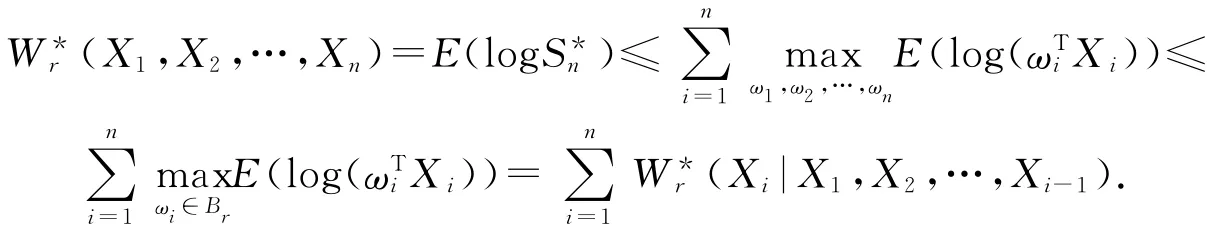
即

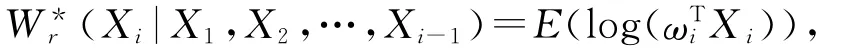
但由于集合Cr的限制未必能达到），从而有

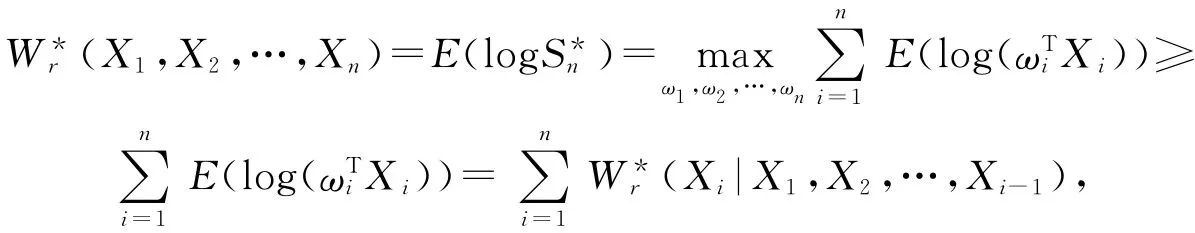
即

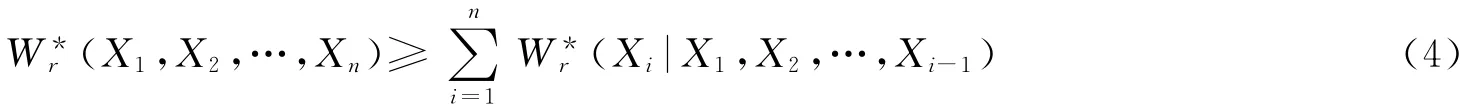
由（3）～（4）式可知

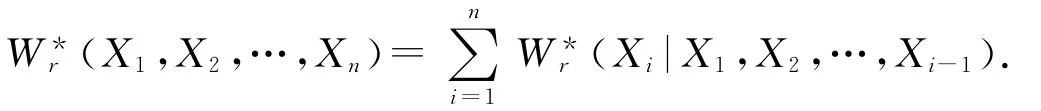
类似定理2的证明，可以得到如下定理．

定理4 设｛Xn，n≥1｝为收益向量序列，记，即Zi为第i个周期达到log－最优组合投资的log－收益，若它是一类负相依序列，即

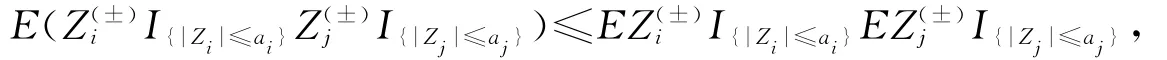
其中i≠j，i，j＝1，2，…．而Zi满足

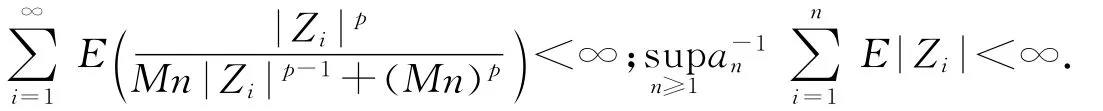
［1］叶中行，林建中．数理金融［M］．北京：科学出版社，2000．

［2］刘莉，周红霞．允许卖空的log－最优资产组合投资模型［J］．应用数学，2002，15（2）：97－101．

［3］黄敏，黄朝炎．一类负相依随机变量序列线性形式的强稳定性［J］．湖北大学学报：自然科学版，2011，33（3）：346－350．

［4］陆传荣，林正炎．混合相依变量极限理论［M］．北京：科学出版社，2000．

［5］Ye Z X，Li J．Optimal portfolio with risk control［J］．Applied Probability and Statistics，1998，14（3）：326－338．

［6］Pham H．Minimizing shortfall risk and applications to finance and insurance problems［M］．Preprint：University of Mame－la－Vallée，1999．

［7］Schachermayer W．Optimal investmemt in incomplete financial Markets［M］．Geman H，Madam D，Pliska S，et al．Mathematical Finance，Bachelier Congress，Berlin：Springer，2000．

［8］Kabanov Yu M，Striker C．On the optimal portfolio for lévy process［J］．Mathematical Methods of Operation Research，2000，51（3）：357－374．