纳米尺度的极化磁化理论
王洪吉
(天津理工大学理学院,天津300391)
0 引言
众所周知,纳米尺度的物质包含的原子非常多,因此不能直接利用量子力学来讨论.但这种尺度的物质又不能摆脱量子效应的影响,不单纯服从宏观的经典物理理论.截至目前为止,还没有一种非常适合纳米尺度的物理学理论.纳米材料有几种效应:小尺寸效应﹑表面效应﹑量子尺寸效应﹑宏观量子隧道效应和介电限域效应等.笔者认为,在这些效应中,小尺度效应,也就是纳米尺度效应,是最基本的和最重要的效应,因为它是产生和引起其它效应的根源.由于纳米尺度效应,纳米材料的力学、电磁学、光学、热学等性质发生了根本的改变.笔者认为,纳米物质的电磁学性质的改变是最基本的,其它力学、热学、光学等性质的改变是由于电磁学性质的改变引起的.
本文中介绍介质的极化磁化新方程,研究纳米材料的极化、磁化、简并和相变,给出纳米尺度的极化磁化方程、电子自旋的数学和物理模型,研究二维纳米材料和石墨烯传导电子自旋的原因.
1 极化磁化新方程
在经典电磁理论中,有关于介质极化和磁化的方程.如

式中P和M 分别为介质的极化强度和磁化强度,c为真空中的光速,ρp和Ji分别为介质的极化电荷密度和诱导电流密度.根据(1)式和(2)式,笔者曾利用八元数方法给出新的极化和磁化方程[1-4]Δ

(3)式说明磁化过程中不会产生磁荷,磁荷的不存在从一个侧面证明了(3)式的正确性.(4)式说明变化的磁化场,产生涡旋的极化场,磁化过程和极化过程是相互关联、共同存在的.(1)~(4)式与麦克斯韦方程组类似,根据(1)~(4)式还可以得到极化强度和磁化强度的波动方程[3],证实了极化波和磁化波也可以光速c在介质中传播.将(4)式整理并和法拉第电磁感应定律相加,可得到

(5)式是用电位移矢量D和磁场强度矢量H表示的法拉第电磁感应定律,是普遍适用的.在真空中,极化强度矢量P=0,磁化强度矢量M=0,(5)式简化为法拉第电磁感应定律.
2 纳米尺度的极化、磁化、简并和相变
宏观电介质在外电场的作用下,会发生极化现象.电介质的极化用电偶极矩描述.在纳米尺度下,材料中的电子有了新的排列方式.比如,有些金属导体,在纳米尺度下,其原子的自由电子被束缚,可能成为绝缘体.这些金属产生了极化现象,这种极化不是在外电场的作用下发生的,而是由于介质的尺寸减小到纳米尺度产生的,笔者认为这种极化可以称为纳米极化.纳米尺度下材料中的极化,也可以用电偶极矩描述.
通常电子材料中电子自旋的取向杂乱,一半自旋向上,另一半自旋向下.经典的电磁学理论忽略了电子的自旋.在纳米尺度下,材料中的电子自旋不能忽略,呈现一种新的有序状态,纳米材料被磁化了,本人认为这种磁化可以称为纳米磁化.比如,在三明治的单晶巨磁电阻材料中,电子自旋的分布是有序的.在没有外磁场情形下,两边的铁磁层中的电子自旋方向相反.又比如,在轨道与自旋耦合的自旋霍尔效应的纳米尺度的拓扑绝缘体材料中,在没有外磁场的情况下,电子自旋的方向也呈现了一种反对称分布.
普通大块晶体内含有大量原子(或原胞),其能带中的能级间距很小,呈准连续结构.纳米尺度的晶体只能包含有限数目的原胞,使能级离散化,能级出现了明显的简并现象.这种简并状态是在纳米尺度下出现的,可以称为纳米简并.这种能级的简并与材料的极化和磁化以及电子的有序分布相对应.
纳米尺度的物质不仅由于尺度效应会自发出现极化和磁化现象,而且还会发生相变.比如铁磁质的磁畴,在某个纳米尺度会转变为单个粒子的磁畴.这种相变可以称作纳米相变.
以上的极化、磁化、简并和相变都是小尺度效应、即纳米尺度效应导致的.
3 纳米尺度的极化磁化方程
在经典电磁理论中,介质的极化强度P和磁化强度M 分别由微观物理量电偶极矩pi和磁偶极矩mi定义.将介质的极化强度P的定义式和介质的磁化强度M 的定义式

分别代入(3)式和(4)式,并化简,得[3-4]


在纳米尺度时,材料会发生纳米极化和纳米磁化现象,电子的个性(单个效应),量子效应(离散化效应)明显显现出来,如库伦堵塞效应、电子自旋效应、单粒子磁畴、轨道自旋耦合、能级简并、能级分裂、相变等.根据(8)式、(9)式以及物质在纳米尺度时的状态,不同于该物质在整体状态时所表现的物理状态.假定在纳米尺度时以下方程成立 Δ(11)式表明,纳米尺度的微观客体,其电偶极矩pi与磁偶极矩mi是互相关联的.
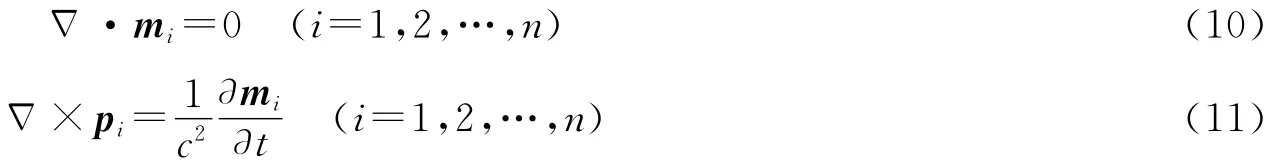
(10)式、(11)式为纳米尺度下物质的极化磁化方程.从数学上分析,(10)式、(11)式仅是(8)式、(9)式成立的充分条件,不是必要条件.由于磁荷不存在,(10)式是正确的.
宏观尺度的物质是集体化的,由(3)式、(4)式或(8)式、(9)式描述.电子的自旋正负抵消,对外不显现其作用,除铁磁材料等例外.
纳米尺度的物质是属于个体的,由(10)式、(11)式描述.此时个性突出,电子自旋不再互相抵消,物质中的电偶极矩不再互相抵消,出现了纳米极化、磁化、简并、相变等物理现象.
4 电子自旋的数学和物理模式
在数学上,矢量函数A(t)模不变的的充分必要条件是[5]

电子的自旋量子数等于±1/2,电子的自旋角动量是矢量,角动量是轴矢量,因此把电子自旋看成模等于1/2的轴矢量.磁偶极矩mi是轴矢量.可以利用磁偶极矩mi表示电子的自旋,因此表示电子自旋的磁偶极矩mi的模为1/2,是模不变的矢量.于是有[4]

即电子自旋矢量与其导矢量互相垂直.根据(11)式,电子极化产生的电偶极矩与电子的自旋矢量在同一平面,是共面的.
设有矢量场A,若其散度Δ·A≡0,则称此矢量场为管型场或无源场.矢量场A为管型场的充分必要条件是它为另外一个矢量场B的旋度场[5].因此由(10)式,mi也可以表示为另外一个矢量的旋度.

若磁偶极矩mi看作是电子自旋磁矩的表达式,则电子的自旋是矢量ci的旋度,电子自旋是个旋度.旋度是矢量,其大小为环量面密度的最大值,其方向为环量面密度最大值的方向.环量是沿闭合曲线的曲线积分,环量面密度是闭合曲线对其所包围的面积的比值的极限,即环量对面积的变化率.磁偶极矩的物理模型是闭合电流产生的磁矩.因此,数学模式与物理模型吻合[4].
根据磁化电流密度的定义,定义
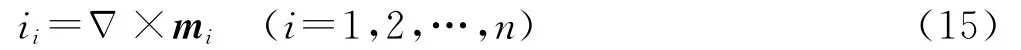
为电子自旋的磁化电流密度.电子自旋的磁化电流密度也是旋度,但是与电子自旋不同的是,电子自旋的磁化电流密度是极矢量,电子自旋是轴矢量.
利用(11)式、(13)式和(15)式,可以分析纳米材料中电偶极矩方向、自旋磁矩方向、自旋极化电流方向(自旋的磁化电流密度方向)、自旋旋转变化方向.下面将利用这些表达式研究二维纳米材料和石墨烯.
5 二维纳米材料研究
由于一维纳米材料可以看成二维纳米材料的特例,一些功能材料薄膜都属于二维纳米材料,二维纳米材料是比较典型的纳米材料.有一维是纳米尺度,另外两维为宏观尺度的二维纳米材料.为便于描述,把它简化为无限大平面.由于纳米尺度的尺度效应,材料自发发生了极化和磁化.磁化使材料中电子的自旋不能忽略不计.极化出现了电偶极矩,假定电偶极矩的方向与平面平行.根据(11)式和(13)式,电子自旋的方向也与平面平行.根据(15)式,电子自旋的磁化电流密度(电子自旋的极化电流)的方向垂直于平面.
在巨磁电阻的三明治结构中,电子的自旋方向,电子的自旋极化电流密度的方向恰好满足这种结构.电子自旋方向在平面内,电子的自旋极化电流密度的方向垂直于平面.
6 石墨烯传导电子自旋的原因
石墨烯是由碳原子组成的二维晶体,仅有一层碳原子的厚度.石墨烯是目前人们发现的最薄和最硬的一种材料,其导电和导热性能极强,几乎完全透明,而且能有效传导电子自旋,电子在其中能象光子一样高速运动.因此,石墨烯在很多方面都具有潜在的和重要的应用价值.
如前所述,电子的自旋是矢量的旋度.旋度是矢量,是环量面密度,其方向为最大的环量面密度的方向.而石墨烯由非常对称的环状的键组成,具有天然的环状结构.因此石墨烯的几何结构与电子自旋的数学结构相同.把蜜蜂比作电子的自旋,而石墨烯恰好就是蜜蜂的蜂窝.石墨烯本身的结构是传导电子自旋的“桥梁”.因此石墨烯能有效的传导电子的自旋.
根据以上分析,若电子自旋方向垂直于石墨烯平面,根据(15)式,电子自旋的磁化电流密度平行于石墨烯平面,与电子的自旋矢量垂直.
另外,根据(1)~(4)式可以得到极化强度和磁化强度的波动方程.极化波和磁化波可以以光速在介质中传播.
与石墨烯类似的六角环状结构的纳米晶体,都有可能成为传播电子自旋的合适材料.硅烯具有与石墨烯类似的六角环状结构,现已证实具有与石墨烯类似的电子结构.
7 结果讨论
本文中的简化处理,忽略了温度等其它因素.事实上,在纳米尺度,材料的相变温度发生了变化,很多其它因素是不能忽略的.
纳米尺度的极化磁化方程和理论,电子自旋的数学和物理模型,只是为解释纳米材料的极化磁化现象提供的一种新线索和新方法,并不是取代其它纳米理论和方法.
电子自旋是旋度,电子自旋的磁化电流也是旋度.粗略地说,旋度是闭合环路积分对面积的最大变化率.凡是具有环状的纳米材料都适合电子的自旋和自旋的磁化电流(极化电流).
[1]王洪吉.八卦数学物理原理[M].香港:中国国际教育出版社,2002.
[2]Wang Hongji.The application of octonion to physics[C].Beijing:Higher Education Press,2002:292-293.
[3]王洪吉.介质极化和磁化的八元数理论[J].商丘师范学院学报,2003,19(2):25-27.
[4]王洪吉.极化和磁化方程应用研究[EB/OL].http://www.paper.edu.cn/releasepaper/content/200711-553.
[5]谢树艺.矢量分析与场论[M].北京:人民教育出版社,1978:8-56.

