一种常微分方程数值计算的新方法

孟波，孟纯青

（1．联科应用研究所，山东 济 南250031；2．山东省济南中学，山东 济 南250001）

0 引言与基本知识介绍

提出一种构建常微分方程数值方法的新思路，按照这种思路，构建一些具体的计算公式．先介绍一阶和二阶偏差分．

对于函数f（x，y）在点（xi，yi）处的的一阶形式如下．

对于二阶偏差分有以下形式．

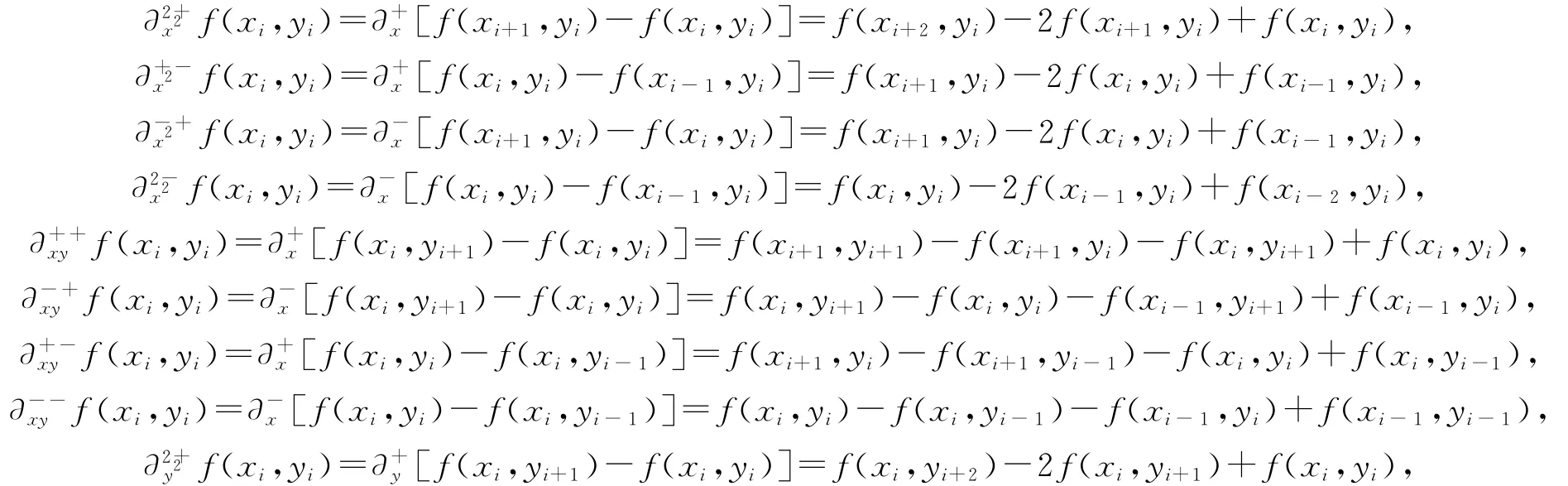
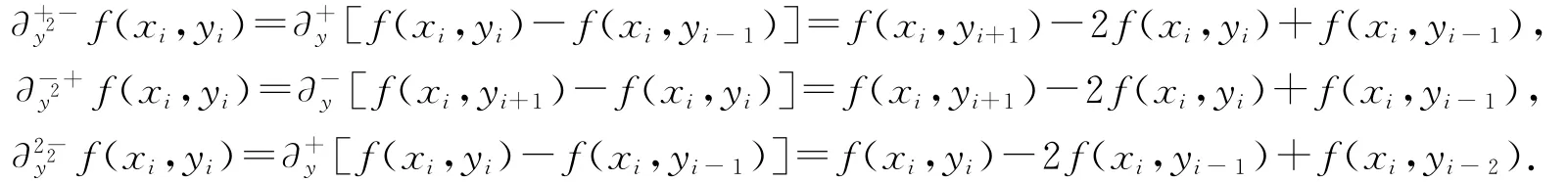
最后给出两个变量的两种Taylor公式．

1 新方法的基本思想与相关公式的推导

设存在常微分方程初值问题f（x，y）关于y满足Lipschitz条件，即对于y1、y2有｜f（x，y1）－f（x，y2）｜≤L｜y1－y2｜．设步长为h，这时有xi＋1＝xi＋h，xi－1＝xi－h．现在介绍新方法的基本思想．

如果假设yi＋1－yi＝ki，忽略余项，（1）式和（2）式可以写成以下形式：

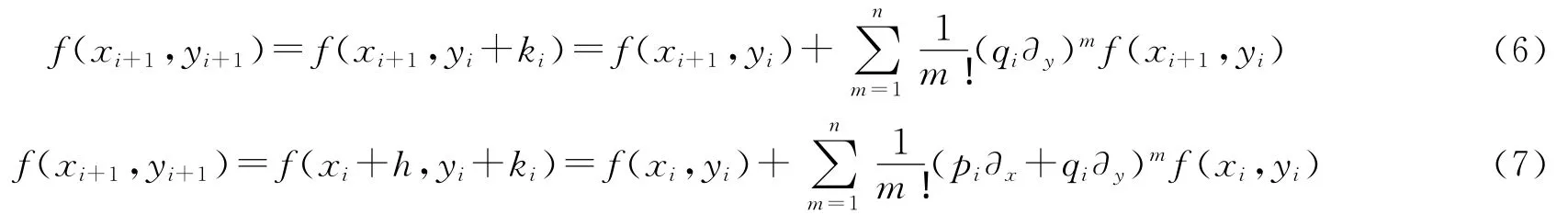
把（6）～（7）式跟一些传统方法结合起来就得到新方法中的公式，这些公式的形式可参见文献［1－3］．

隐式Euler方法的形式为：

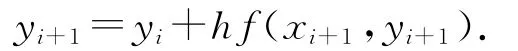
如果把右边的f（xi＋1，yi＋1）按照（6）～（7）式展开后得到

公式（A1）、（A2）就是两种n阶新方法中的公式，其中（A1）是按照（6）式推导出来的，称为新方法中的单差分公式，（A2）式是按照（7）式推导出来的，称为双差分公式．选择具体的偏差分形式可以构建不同的计算公式．下面就是一些具体公式．

如果只考虑到一阶偏差分，对于（A1）式，设0≤r≤1，记：

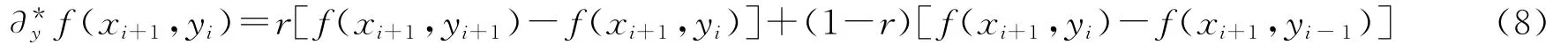
有计算公式：

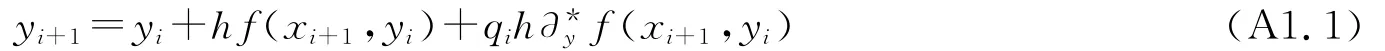
对于（A2）式，设0≤r1，r2≤1，记：

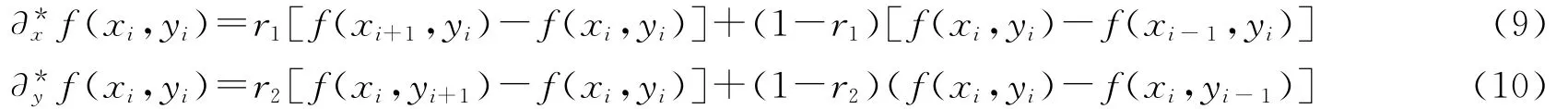
有计算公式：

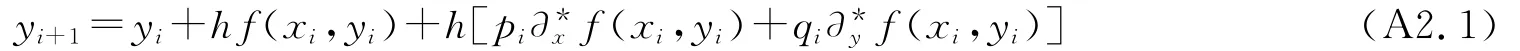
设0＜s＜1，把以上思想用于加权梯形公式得到：

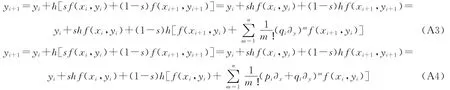
如果只考虑到一阶偏差分，把（8）～（10）式代入得到以下公式：

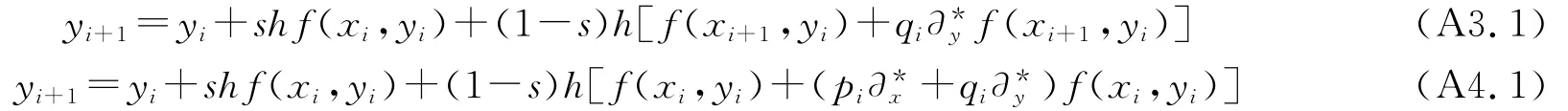
如果只计算到二阶偏差分，公式（A4）的一种具体形式为：

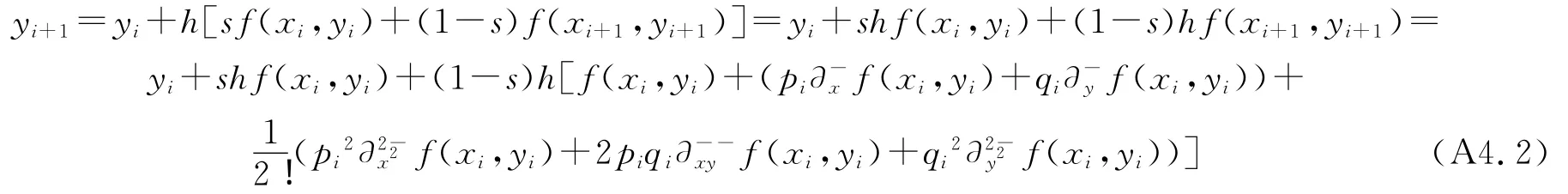
把以上思想和其他公式相结合，可以得到许多新方法中的公式．

与Adams隐式方法相结合可以得到许多公式，以下仅列出从三阶、四阶Adams隐式方法推导出来的新公式．

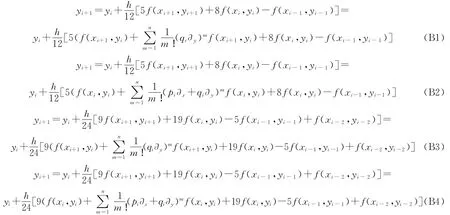
如果计算到二阶偏差分，公式（B4）的一种具体形式为

从Gear方法中可以推出许多新方法中的公式．以下给出三步新方法中的公式

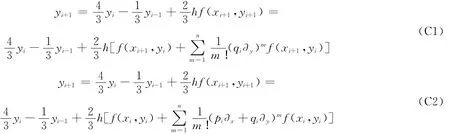
如果只计算到二阶偏差分，公式（C2）的一种具体形式为：

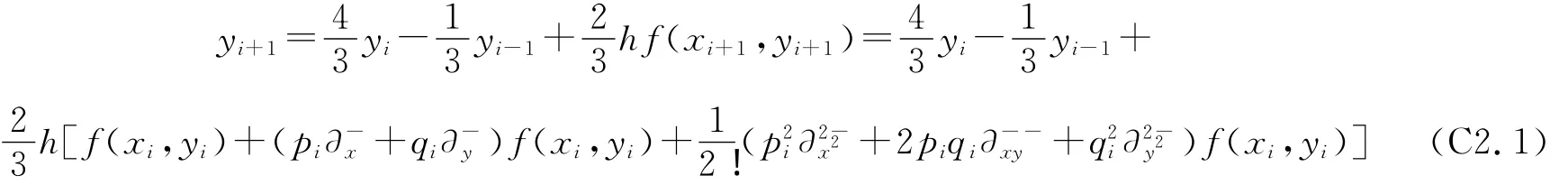
用以上思想可以构造出许多新方法中的公式，这类公式数量极多，本文中不再一一列举．

2 新方法中的加权平均公式和预估校正公式

按照笔者的思路，可以构造很多具体的加权平均公式和预估校正公式，限于篇幅分别给出一例．

设存在r1，r2，满足0＜r1，r2＜1，则（A1）式和（A2）式的加权平均公式为：

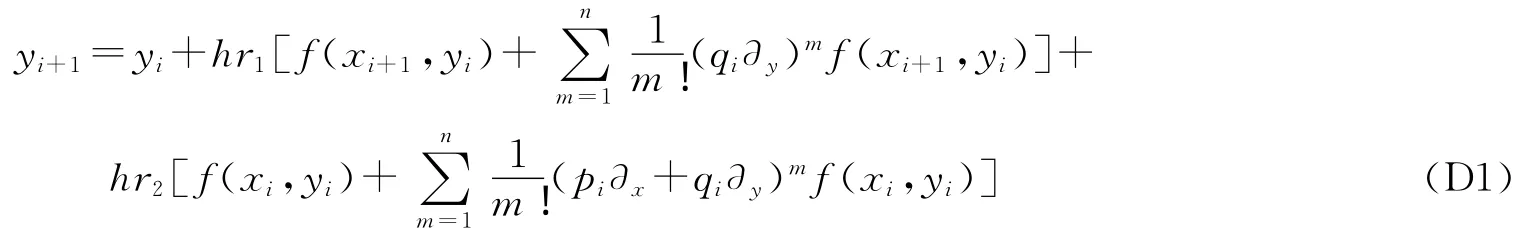
使用具体的r1，r2，构建具体的加权平均公式，按照以上思路，可以构造出许多加权平均公式．

新方法中的显式公式可以跟隐式公式相结合形成预估校正公式（A4．1）中一个的具体公式和梯形公式组成的预估校正公式为：

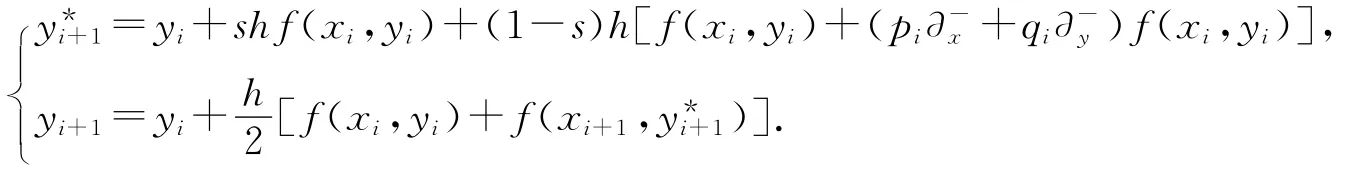
3 pi、qi值的确定

以上算法中出现了pi、qi两个参数，现在来讨论pi、qi的计算方法，计算方法可以有多种形式．

如果假设∂xi＝dxi＝h，即dyi＝hf（xi，yi），则

如果存在常数r1，r2，满足∂yi＝r1（yi＋1－yi）＋r2（yi－yi－1），则：

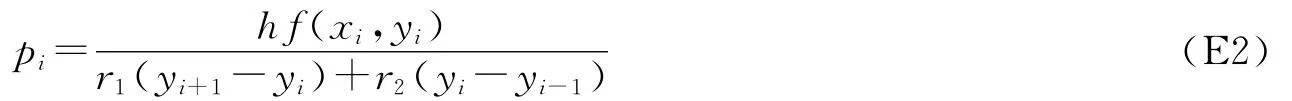
对于qi则可以有以下选择．

如果假设∂yi＝yi＋1－yi，那么

如果假设∂yi＝yi－yi－1，那么

如果存在常数r1，r2，满足∂yi＝r1（yi＋1－yi）＋r2（yi－yi－1），那么：

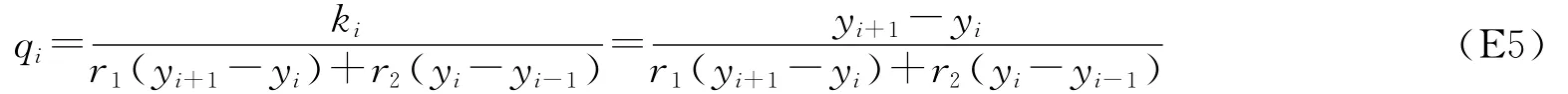
由于（E2）式、（E4）式、（E5）式出现了yi＋1，这就变成了隐式公式．为便于计算，可用一些近似方法．

一是直接计算方法：把某种显式公式代入直接给出yi＋1的表达式；二是采用预估校正的方法得到相应的计算公式．以下给出几个具体公式．

直接计算公式．如果假设yi＋1＝yi＋hf（xi，yi），则代入（E2）式、（E4）式得到

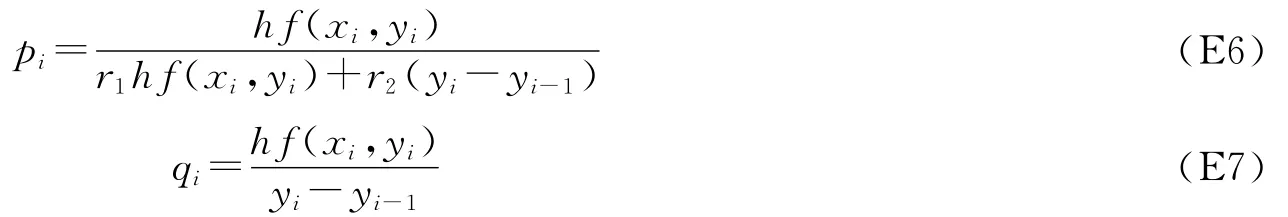
代入（E5）式得到

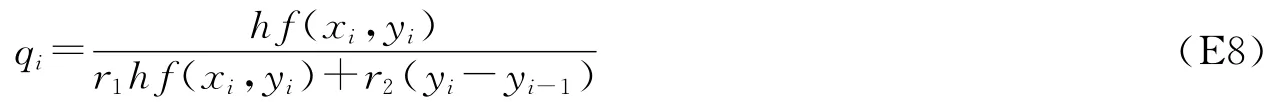
预估校正公式有很多，下面介绍两种．

一阶单差分预估校正公式：

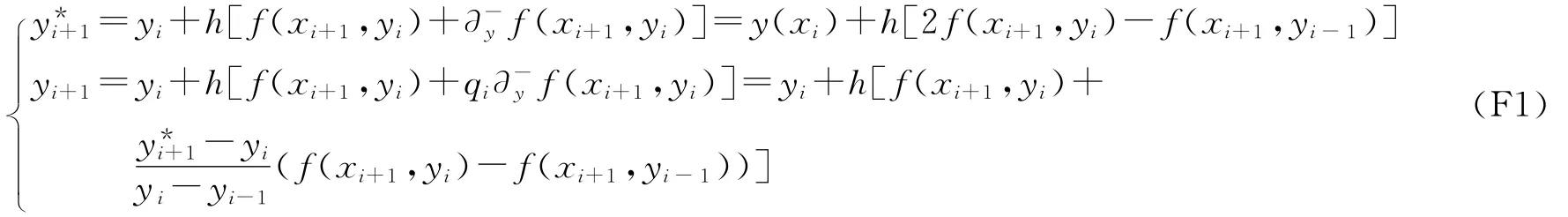
二阶双差分预估校正公式：

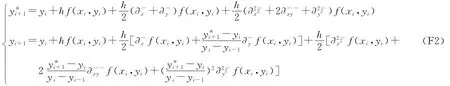
直接计算公式和预估校正公式还可以有其它形式，限于篇幅本文只给出以上形式的公式．

4 递进计算公式

实际计算时，为了提高精度，可以采用递进计算公式，计算步骤如下：

对于显式公式，当计算第i＋1步的数值时，可以使用第i，i－1，i－2，…，i－j步时的数据，这样可以按照实际的计算步数来确定计算公式的阶数．当计算第一步数据时，j＝1，当计算第二步数据时j＝2，当计算第k步数据时，j最多可以等于k，这样层层递进从而得到一个递进计算公式．递进计算公式实际上是一个变阶计算公式．

5 相容性、收敛性和稳定性分析

以下讨论相容性，收敛性和稳定性．这涉及到qi的表达式的选择，由于yi＋1可以预估而yi，yi－1已知，这样每一个qi也可以得到一个预估值．所以下面的讨论将每一个qi当作常数．

先讨论相容性．限于篇幅，仅讨论（A2．1）式，为了简便起见，设，对于（A2．1）式，取，显然当h→0时，均有偏差分∂xf（xi，yi）→0，∂yf（xi，yi）→0，于是ψ（x，y，0）＝f（x，y）．因此方法具有相容性．

下面讨论收敛性．对于（A2．1）式，为了简便起见，设r1＝0，r2＝0．对于y1，y2，有

设｜y1－δ－y2－δ｜＝w｜y1－y2｜，则上式满足

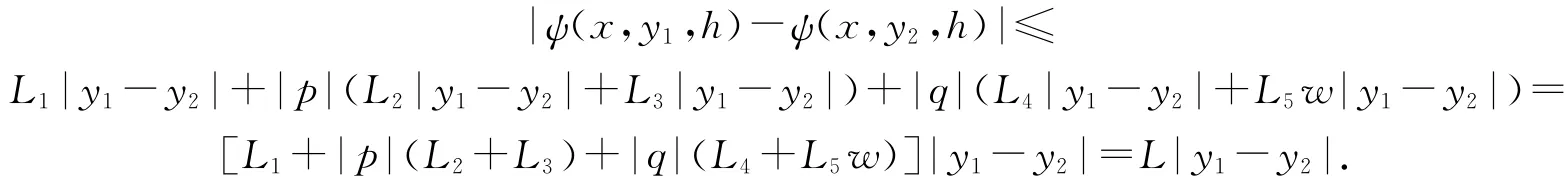
因此ψ（x，y，h）关于y满足Lipschitz条件，再考虑到相容性，故算法是收敛的．可用类似的方法讨论其他新方法的相容性和收敛性．

最后讨论稳定性．限于篇幅以下仅讨论（A3）式和（A4）式的稳定性．设存在以下实验方程：

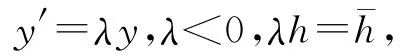
代入（A3）式或（A4）式，这时两个公式一样．现给出代入（A4）式的情形．设s＝0．5．

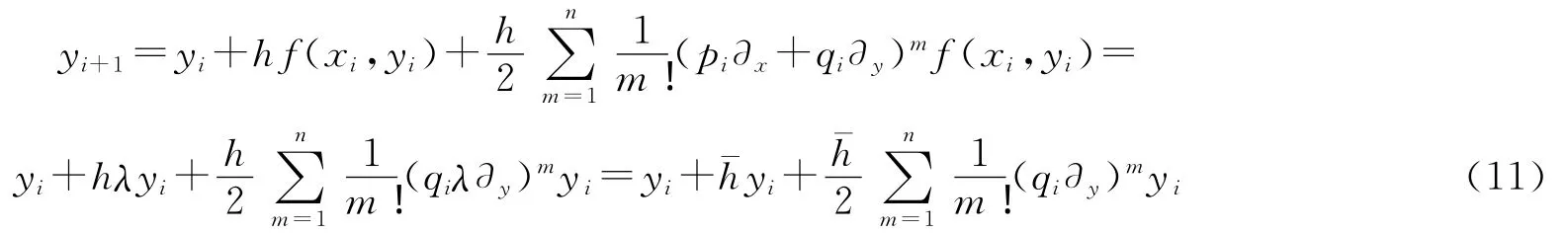
限于篇幅，以下仅讨论到n＝1时的情况．如果取∂yyi＝∂yi＝yi－yi－1，qi＝1代入（11）式有：

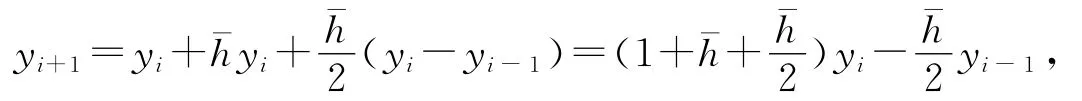
移项后得到：

相应的特征方程为：

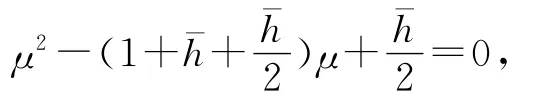
如果取∂yyi＝∂yi＝yi＋1－yi，代入（11）式有：

移项后得到：

6 实例计算

例：求解下列常微分方程初值问题，y′＝x－y＋1，y0＝1，h＝0．1，0≤x≤1．

本例有精确解y＝x＋e－x，其传统方法的计算结果可见参考文献［4］．为了比较各方法的精确度，以下采用多种方法进行求解，以便比较各种方法的精确度，同一个公式使用pi＝1，而使用不同的qi分别计算，以便观察计算精度．

现把一些相关的计算公式列举如下：公式（B4．1），公式（C2．1），（A4．2）．以上公式分别根据不同的qi的值或者表达式进行计算．

表2给出了公式（B4．1），公式（C2．1）的计算结果，其中前3个公式为（B4．1）的计算结果，后3个公式为（C2．1）的计算结果．6个公式的参数分别为：

在计算中由于一些公式是高阶公式，所以前两个或3个值使用精确解的数值．前3个精确值为：y0＝1，y1＝1．004 837 418，y2＝1．018 730 753．计算结果如下：

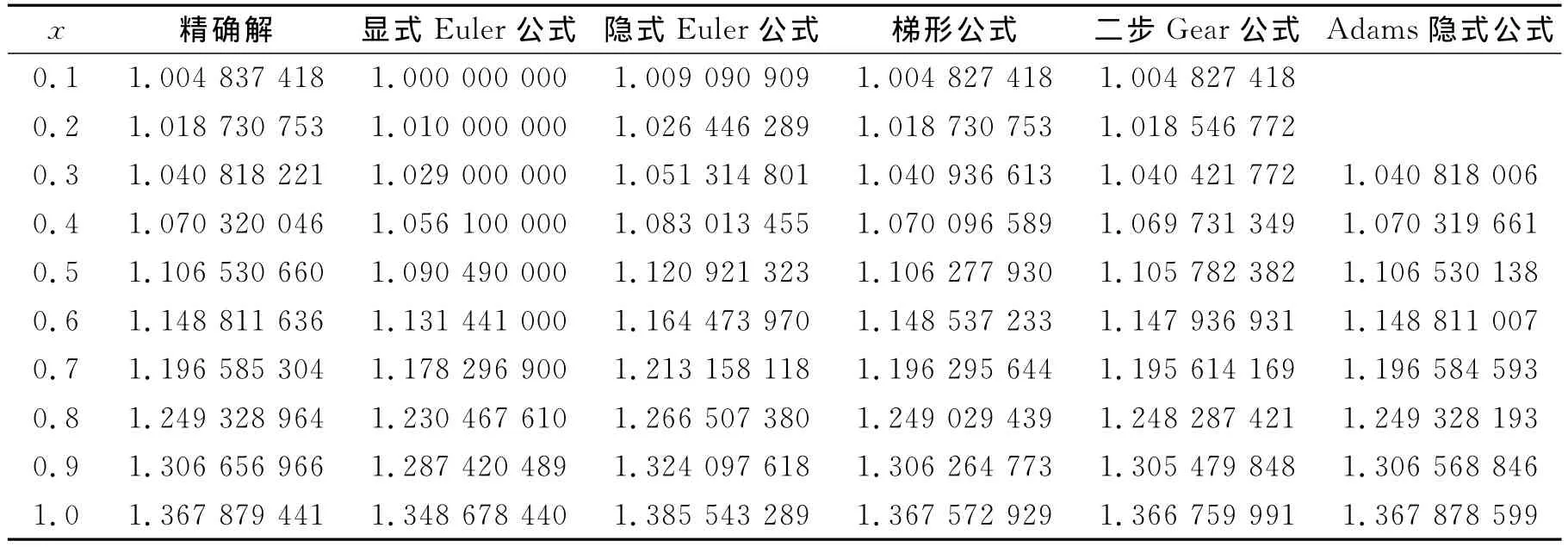
表1 传统公式计算结果及精确解

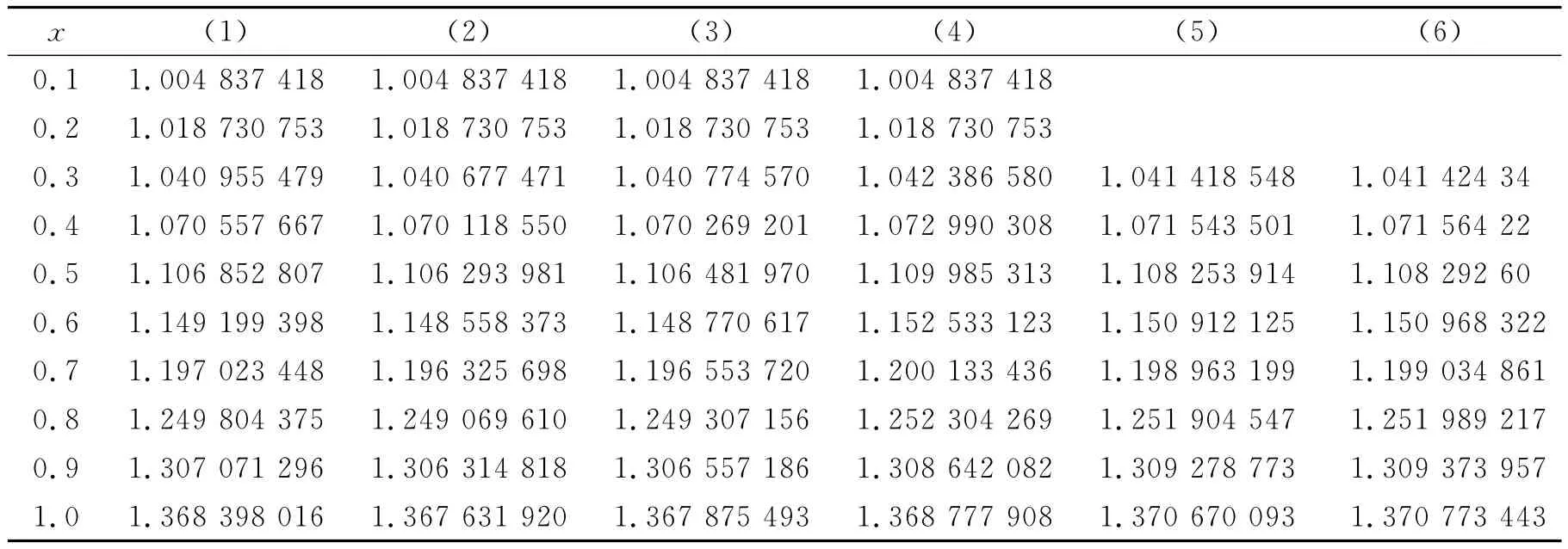
表2 公式（B4．1）、（C2．1）的计算结果

表3 公式（A4．2）的计算结果

从以上计算结果看出：以上公式的计算结果明显好于隐式Euler公式，（C2．1）式的计算结果与两步Gear公式相当，精度高低跟选择的具体参数有关，（B4．1）式的3个公式计算结果比隐式Adams公式略差，（A4．2）式的计算结果跟梯形公式大致相当，精度的高低跟具体的参数选择有关，第5个公式的计算结果跟精确解非常接近．

新差分方法具有以下特点：可以把隐式公式变成显式公式，这大大减少了计算难度；二是可根据不同的差分形式得到种类繁多的具体计算公式．可以根据具体情况酌情使用，这对实际计算非常有利；三是可以构造出种类繁多的加权平均公式．笔者认为，新方法是一种值得认真研究的常微分方程数值方法，具有极大的理论价值和应用价值．

［1］李荣华，刘播．微分方程数值解法［M］．4版．北京：高等教育出版社，2009：1－40．

［2］戴嘉尊．微分方程数值解法［M］．南京：东南大学出版社，2012：1－45．

［3］倪兴．常微分方程数值解法及其应用［D］．合肥：中国科学技术大学，2010．

［4］王立秋，魏焕彩，周学圣．工程数值分析［M］．济南：山东大学出版社，2002：350－370．