电子自旋角动量的升降算符*
呼和满都拉,丽 丽,杨洪涛,冀文慧,韩明初,孔令茹
(1.集宁师范学院;2.呼伦贝尔学院)
1 电子自旋角动量的升降算符的推导
以表示电子自旋角动量算符,假设其分量都是厄密的,等等)而且满足与轨道角动量一样的对易式,即

亦即

这样假设的理由是,轨道角动量曾从这种对易式出发,导出角动量(平方及投影)的本征值,其中的情况刚好和电子自旋相符合.
根据实验测量,S在任何方向的投影的取值只能是,因此成立下列算符关系:
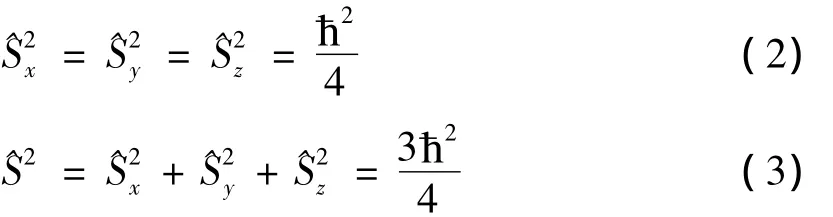
(1)至(3)式包括了电子自旋角动量的全部性质.其中(1)式是任何角动量的共性.(2),(3)式则是电子自旋特有的.
为了简化运算,引入无量纲的“泡利自旋算符”σ,

则(1)式变成

亦即

(2)式变成

(3)式变成
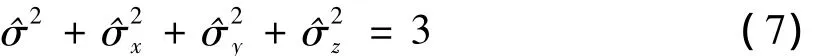
以σx分别从右和左乘(5)式,再利用(6)式,易得

类似地可证

以(8')式代入式(5),既得

(6),(8),(9)式可以统一成一个公式
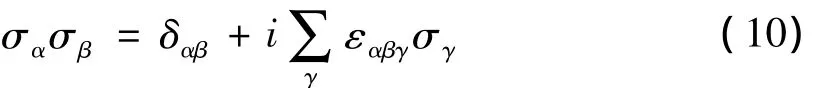
其中α,β,γ各自代表(x,y,z)三个分量中任何一个,εαβγ为 Levi- Civita 符号,定义为[1]
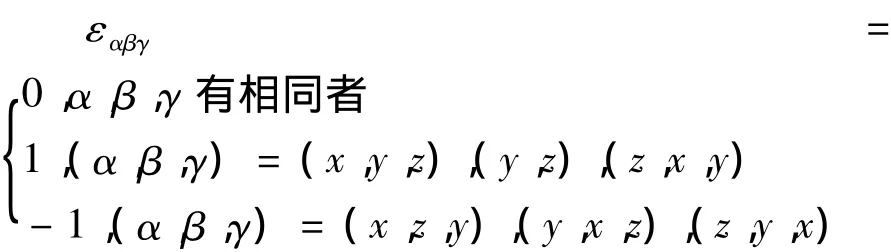
由于Sx,Sy,Sz互不对易,没有共同本征态,电子的自旋状态一般只能采用下述表达方式.任取的一个分量Sz,以它的本征态作为基本自旋函数,任何自旋态则表示成这些本征态的线性叠加.Sz取本征值时,本征态记为或α,本征值的本征态记为χ1或β即
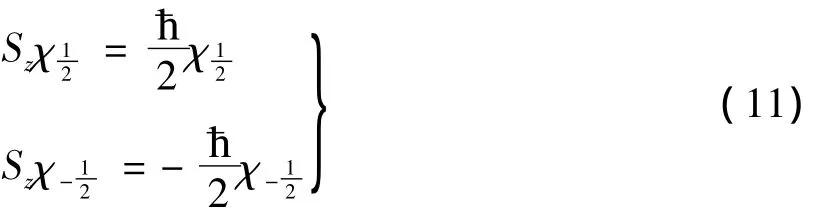

电子的任何自旋态χ可以表示成
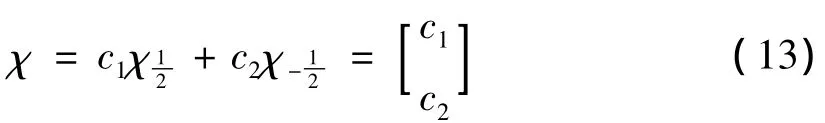
这就是以Sz作为自旋变量时自旋波函数的表示形式,所以(13)式左端也可写成χ(S2),c1和c2就是当S等于±时波函数χ的值,c和c的概z12率含义则是
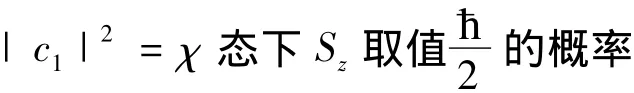

当然,自旋波函数应该满足归一化条件
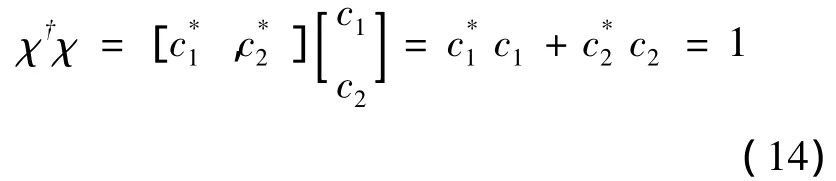
在Sz表象中,S及σ各分量应该表示成二阶厄密矩阵,其中Sz,σz为对角矩阵,对角元等于本征值.因此可以直接写出
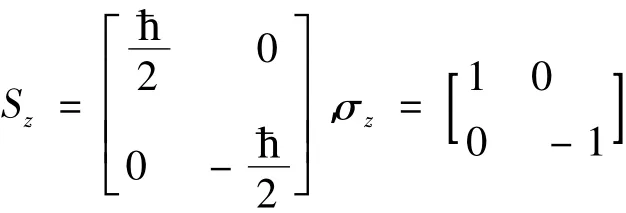
下面来确定σx和σy的矩阵表示,设[1]为实数,因为
由(8)式,易得a=c=0,而由(6)式,又得bb*=1至此已经没有公式可以利用了.作为一种简明的选择,取b=1,则

再利用(9)式(σzσx=iσy),即可定出σy,总的结果是
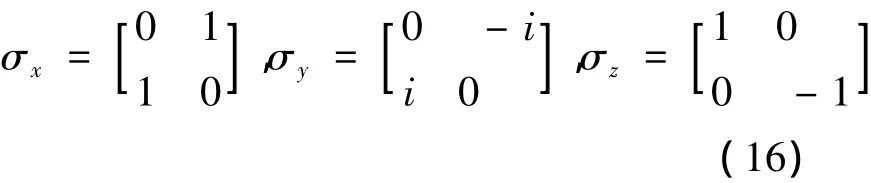
这就是著名的泡利矩阵.容易验证,这三个矩阵满足(6)至(9)全部关系式,泡利矩阵对于及的作用结果是

因此
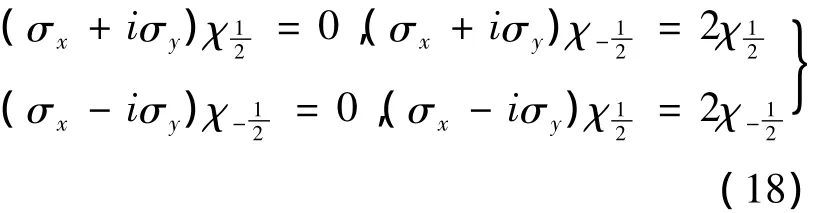
如将σ换成S,(18)式就是
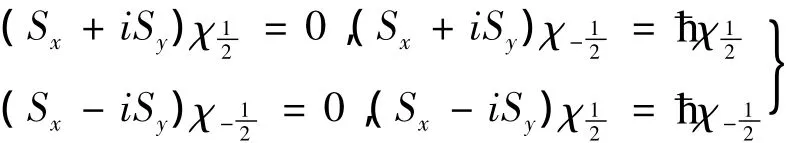
2 电子自旋角动量升降算符的性质
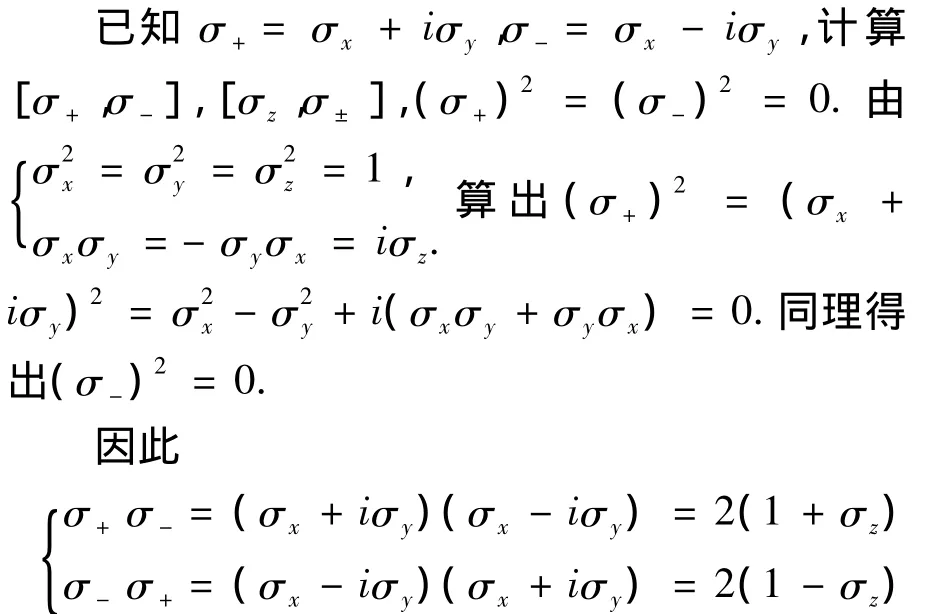
所以[σ+σ1]=4σz.
另外可得[σz,σ+]= [σz,σx]=i[σz,σy]=2σ+.
取共轭可得[σz,σ-]=-2σ-.
通过此题能深刻理解电子自旋角动量升降算符的性质.
3 电子自旋角动量升降算符的应用
(a)写出它们的具体函数表达式.
(b)对于χ10,说明它是下列哪几个算符的本征函数,本征值等于什么?
分析:(a)由二电子体系可直接写出其4个本征函数.
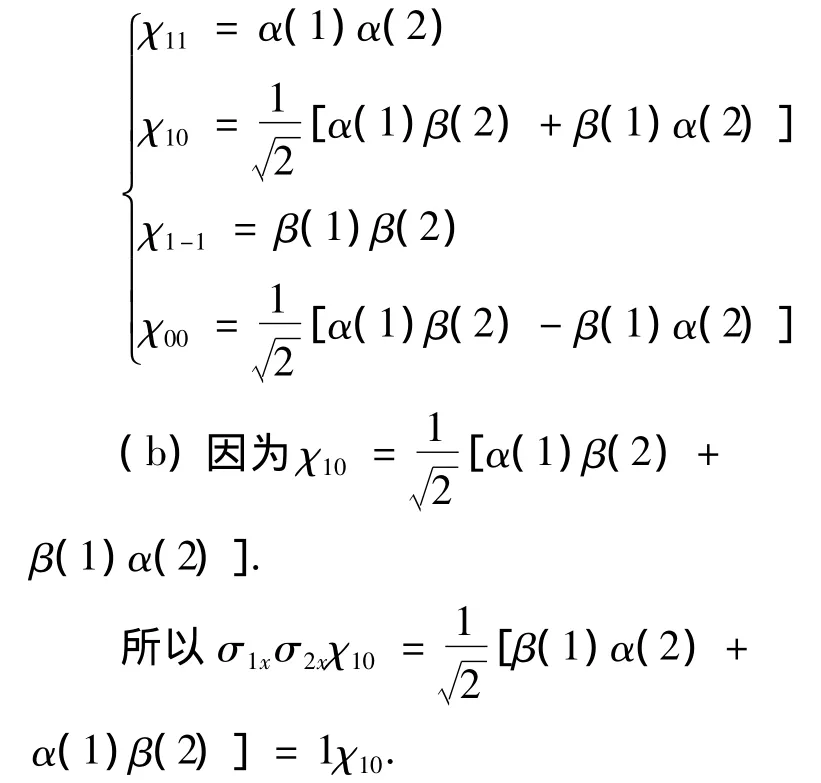

α(1)α(2)],故:χ10不是σ1x+σ2x的本征函数.
通过此题能深刻理解电子自旋角动量升降算符的应用.总结:在量子力学的所有力学量中,电子自旋角动量是最能显示微观世界基本物理特性的物理量之一[2].电子自旋角动量的升降算符的性质是量子力学中非常重要的性质,与其他算符同样重要,甚至重于其他算符,对这些推导及性质的熟练掌握会对解题有很大的帮助,能加深你对算符的理解.
[1]钱伯初.量子力学[M].北京:高等教育出版社,2005:151-162.
[2]周世勋.量子力学[M].北京:高等教育出版社,2009:172-184.

