结合傅立叶变换的差分进化算法在阵列波束展宽中的应用
谢欢欢,李长源,杨伯朝
(中国电子科技集团公司第二十研究所,西安 710068)
在阵列天线设计过程中,为了实现一些特定的目标,需要对阵列的波束形状进行优化设计。在实际应用中,有时要求展宽阵列天线的波束。如相控阵雷达在指定空间区域实现多目标的搜索和跟踪时,要求展宽相控阵天线的波束。相控阵雷达在进行宽波束搜索、多目标引导和宽波束导弹截获时,也需要其阵列天线具有宽波束的功能。除此以外,阵列波束展宽还应用于空间微波能量传输中,波束展宽能避免能量过于集中,对接收的整流设备造成击穿破坏,使能量在要求区域内均衡分布,接收设备的效率最大化。研究人员提出了很多阵列赋形算法来实现波束展宽,其通常可分为解析方法和数值方法。经典的解析方法有傅立叶变换法(Fourier Transform Method)[1]、Woodward综合法[2]等,这类方法计算速度快,但其精度较差,与要求的波形会存在一定差异。与解析方法相比,数值方法的精度高,适用范围广,越来越受到重视。然而数值方法的计算量比较大,存在变量多及方向图综合全局优化较困难等问题。
种群进化类算法在解决多维、非线性、全局寻优方面具有传统算法不具备的优点,在阵列方向图综合方面得到了广泛应用。进化算法中的遗传算法(GA)在降低阵列天线的副瓣电平有较好应用[3]。粒子群优化算法(PSO)已成功应用于二维阵列、共形阵列波束优化上[4-5]。差分进化算法是一种在连续空间中进行启发式随机搜索的智能优化算法[6],差分进化算法已用于阵列天线波束赋形上[7-8]。然而目前的进化类智能算法都存在易陷入局部最优、容易早熟、收敛速度慢的问题。
本文使用差分进化算法结合傅立叶变换的初值对阵列天线波束进行展宽设计。该方法首先使用傅立叶变换计算展宽后阵列天线的幅相,将得到的幅相作为差分进化算法的一个初始值进行进一步的优化计算。这能提高傅立叶变换计算的精度,使展宽后的波束效果更好。而以一个相对较优的幅相值作为差分进化算法的初始值时,能使差分进化算法的收敛速度更快,避免陷入局部最优的现象。使用该方法对一个21元的一维直线阵进行波束展宽设计。阵列在等幅同相时的3 dB波束宽度为4.02º,使用文中方法展宽波束后,3 dB波束宽度变为19.6º,主波束范围内的平坦度为0.21 dB,优于仅使用傅立叶变换获得的结果。
1 算法原理
该算法将傅立叶级数变换和差分进化算法结合,使用傅立叶级数变换获取差分进化算法其中的一个初始值,再使用差分进化算法对傅立叶级数变换的结果进行优化,获得更佳的波束形状。
1.1 傅立叶级数变换法
N元规则直线阵的阵因子可表示为:

其中,Φ=kd sin(θ),k=2πf /c0,f是工作频率,c0是光速,为3×108m/s,d是单元间距,Am是激励的电流信号,为复数。令参考位置点为阵列的中心,当单元数为奇数时,阵因子为:

当单元数为偶数时,阵因子为:

当m不在阵列区域范围内时Am=0,即单元为奇数时,Am=0( m< -(N -1)/2或m>(N -1)/2);单元为偶数时,Am=0( m<- N/2或 m> N/2)。因而式(2)可转化为:
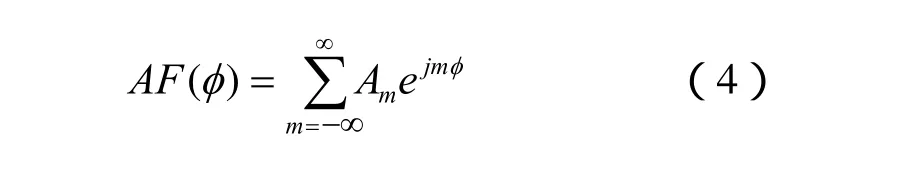
式(3)可转化为:
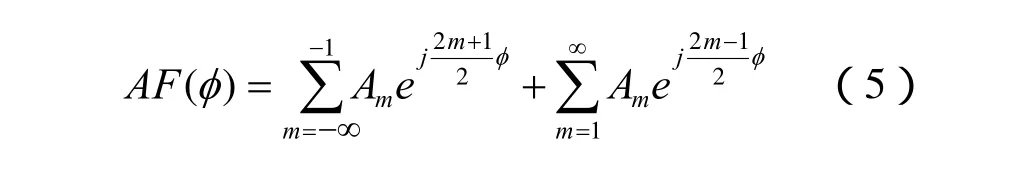
对式(4)和式(5)进行傅立叶变换可得,奇数单元激励的信号为:
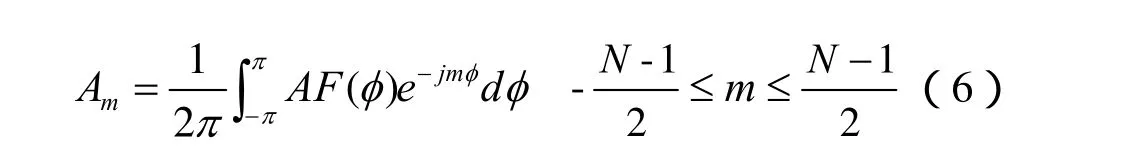
偶数单元激励的信号为:
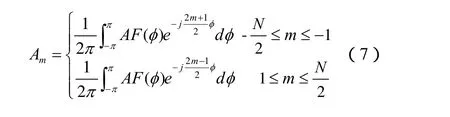
求解的激励信号为复数,包含了激励的幅度和相位。
1.2 差分进化算法
差分进化算法是一种基于种群的随机进化类优化算法,它始于一个随机选择的初始种群向量,主要过程包括初始化种群、变异、交叉和选择[7]操作,重复其变异、交叉和选择操作使计算结果满足设定目标或达到最大迭代次数,计算结束。其计算过程参考文献7。
本文根据算法的实际应用情况,在初始化种群计算时,将其中的一个种群个体设为傅立叶级数变换获得的激励信号,其他NP-1个个体为随机产生。该操作能加速算法收敛速度,避免其陷入局部最优,这里我们令NP个个体的第一个为傅立叶级数变换获得的激励信号,则操作过程如下:
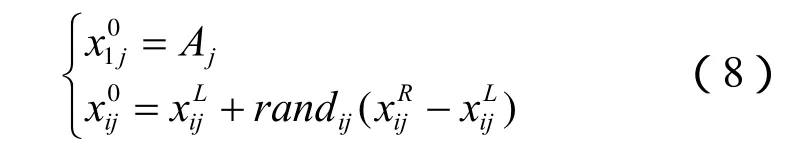
式中,Ai是由傅立叶级数变换得到的幅相值;i =2,3,…,NP,j=1,2,…,D;和分别是第 j个变量的下界和上界;randij是[0,1]之间的随机小数。算法的变异、交叉和选择操作和文献7一致。
2 21元直线阵
为了验证上述方法的可行性,设计了一个21元的直线阵并使用推荐方法进行波束展宽计算。设天线单元为点源,阵列的单元间距d=0.6λ,λ是工作波长,阵列中心为参考的0位置。则天线阵列的电场可表式为:

从图1中可以看到,等幅同相时,天线的3 dB波束宽度为4.02º,副瓣电平为-13.2 dB。

图1 等幅同相情况下,阵列归一化的增益方向图
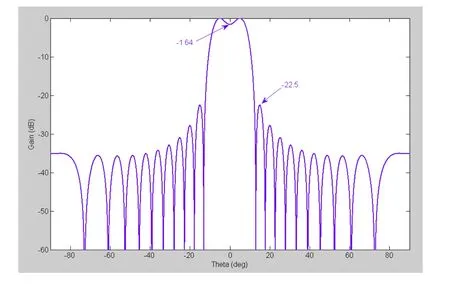
图2 傅立叶级数变换后,阵列归一化的增益方向图
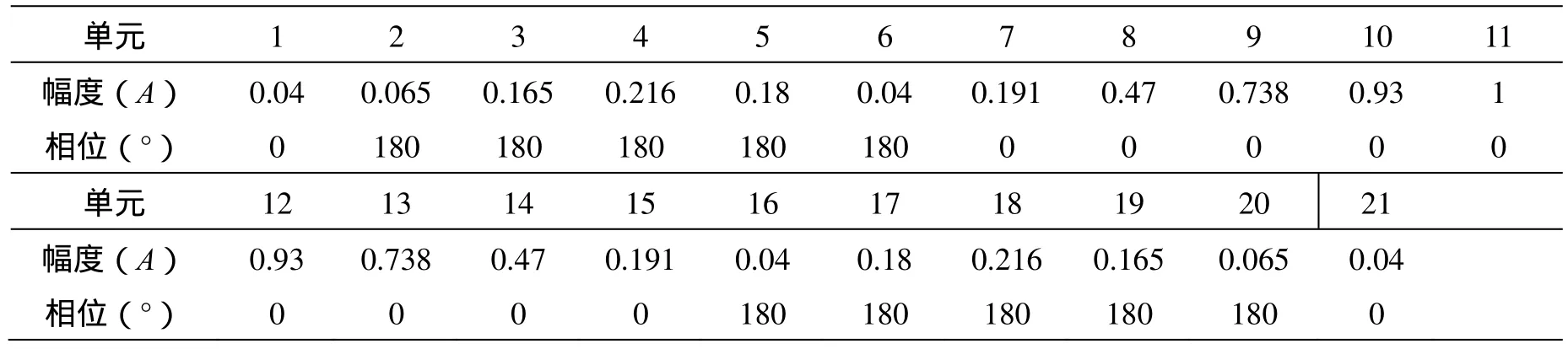
表1 傅立叶级数变换计算获得的幅相值
3 波束展宽设计及结果
将21元直线阵的波束展宽,设计展宽后的3 dB波束宽度为20º,使用傅立叶级数变换法进行计算,得到阵列激励的信号为:

由式(10)计算激励的幅度和相位如表1所示,其归一化的增益方向图如图2所示。从表1数据可以看到,傅立叶级数变换后,得到一些单元激励的幅度很小,如:单元1、2、6、16、20、21,这些端口的幅度都小于 0.1,这会加大单元激励的难度。从表1的数据可以看到,获得的幅度和相位是以中间单元呈现对称关系。从图2的方向图曲线可以看到,阵列的3 dB波束宽度为16.96º,与要求的20º有一定差距。副瓣电平为-22.5 dB,阵列主波束有凹坑,其平坦度为1.64 dB,这说明使用傅立叶级数变换获得的幅相效果不太好。我们以傅立叶级数变换得到的幅相为基础,将其作为差分进化算法其中的一个初始值,进一步提升波束展宽效果,主要从以下三个方面进行改进:
1)增加单元激励的幅度值;
2)提高天线主波束的平坦度;
3)进一步减少副瓣电平。
以此为目标,将激励的幅度设为[0.1,1],波束平坦度设为0,阵列波束的副瓣电平设为-25 dB。则其适应度函数S(θ)可表式为:
G(θ)是由电场方向图E(θ)得到的归一化增益方向图。计算得到的归一化增益方向图如图3所示,其激励的幅度和相位如表2所示。
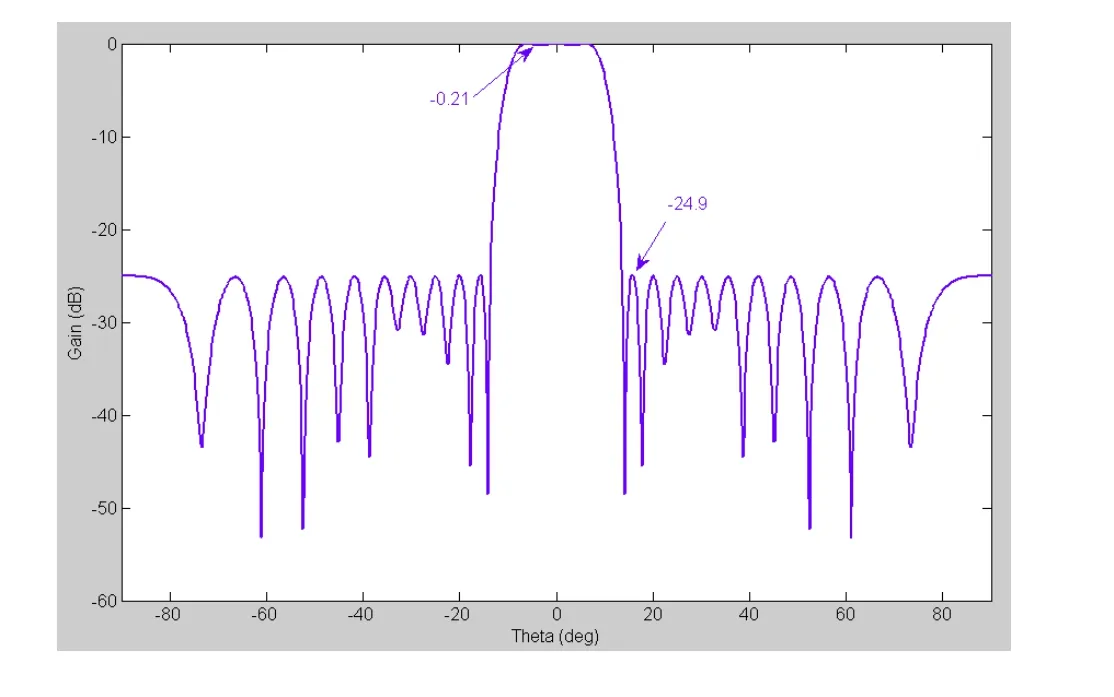
图3 推荐方法计算后,阵列归一化的增益方向图

表2 推荐方法计算获得的幅相值
从表2的数据可以看到,单元激励的幅度都大于 0.1。从图 3可以看到,阵列 3 dB波束宽度为19.6º,幅瓣电平为-24.9 dB,主波束平坦度为0.21 dB,基本达到了设定的要求。
4 结论
本文使用差分进化算法结合傅立叶变换的初值对阵列波束进行展宽设计,该方法比普通傅立叶级数变换获得的波束形状更好,能克服传统差分进化算法收敛速度慢、易陷入局部最优的问题。通过对一个 21元的直线阵进行波束展宽设计,使阵列的3 dB波束宽主扩展到19.6º,主波束范围内的平坦度为0.21 dB,副瓣电平为-24.9 dB,证实该设计方法是切实可行的。
[1]C.A.Balanis, Antenna Theory Analysis and Design [M].Third Edition, Published by John Wiley & Sons, Inc.,Hoboken, New Jersey, 2005.
[2]束咸荣,何炳发,高铁.相控阵雷达天线[M].北京:国防工业出版社.2007
[3]K.K.Yan, and Y.Lu Side Lobe Reduction in Array-pattern Synthesis Using Genetic Algorithm [J].IEEE Trans.Antennas and Propagation, 1997.45(7):1117-1121.
[4]袁智皓, 耿军平, 金荣洪, 范瑜.基于改进的粒子群算法的二维阵列天线方向图综合技术[J].电子与信息学报,2007.29(5): 1236-1239.
[5]D W Boeringer, D H Werner.Efficiency Constrained Particle Swarm Optimization of a Modified Bernstein Polynomial for Conformal Array Excitation Amplitude Synthesis [J].IEEE Trans on Antennas and Propagation,2005.53 (8): 2662-2673.
[6]R Storn, and K.Price, Differential evolution - a simple and efficient heuristic for global optimization over continuous space [J].Journal of Global Optimization,1997.11 (4):3412359.
[7]谢欢欢, 杨伯朝.基于差分进化算法的阵列天线波束赋形研究[J].现代导航, 2012.3: 219-224.
[8]S.Yang, Y.B.Gan, and A.Qing.Sideband suppression in time-modulated linear arrays by the differential evolution algorithm [J].IEEE Antennas and Wireless Propagation Letters, 2002.1: 173-175.

