IIR数字滤波器的仿真实现研究

韩大伟

（河南工程学院，河南郑州 451191）

数字滤波器能通过关系运算转变数字信号的频率，从而进行信号输入输出，它是一种能改变信号频谱的算法装置，是处理信号的利器。人类生活中普遍地出现了数字信号系统，使得数字滤波器设计受到广泛地关注。如今能通过计算机运行MATLAB软件实现IIR数字滤波器的仿真设计。

1 数字滤波器和MATLAB软件

(1)数字滤波器

数字滤波器按照结构的划分，有FIR数字滤波器和IIR数字滤波器。前者非常稳定且具有严格的线性相位，不会造成线条及其边缘部分出现失真现象，广泛应用于通过波传递信息的领域，例如图像传输和数字通信等;而后者的特征则是非线性相位，但较前者而言不但更易实现，且具有较高的经济效益，因此在相位要求不高的领域具有非同寻常的用处，比如说语音通信。

(2)MATLAB软件

MATLAB(matrix＆laboratory)其原意是矩阵实验室，是美国MathWorks公司推出的面向于科学计算、可视化以及交互式程序设计的高科技计算环境，集数值分析、信号处理、矩阵运算以及非线性动态系统的建模与仿真等功能于一体的高度集成系统，它的用户界面极其友好且具有良好的帮助功能，其编辑模式不同于传统的非交互式程序设计语言(如Fortran、C语言等)，标志着国际最先进的科学计算软件水平。

而IIR数字滤波器具有无限持续时间的冲击响应，伴有非线性相位特征，对此本文将探究如何利用MATLAB软件实现IIR数字滤波器的仿真设计。

2 IIR数字滤波器

一般地，由于IIR数字滤波器的系统传递函数包括有两组可调因素，即零点和极点，同时极点能够处在单位圆内的所有位置。因此与FIR数字滤波器相比，它拥有更高的选频特性、更低的通带群延迟，在实现相同频率特性的情况下占据更少的乘法单元，能广泛地应用于高选频、低延迟以及快速处理等领域;但是必须基于相位的非线性之上，往往选择性越好，其相位非线性就越严重，而IIR数字滤波器不具备内禀稳定性及其线性相位不精确，造成其设计的数学模型时常是非线性约束、非凸规划的，从而就必须采用递归结构来配置极点，使之处在单位圆之中。在N阶IIR数字滤波器中，它的传递函数表示如下:

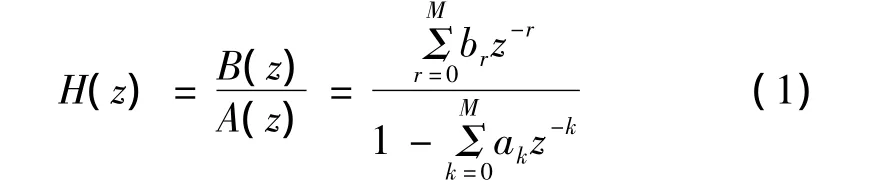
为满足实际需求，大多数情况下M与N取自然数且N＞M;函数A(z)与B(z)是关于z-1的多项式，其中前者是分母多项式，后者是分子多项式;同时M与N分别是分子阶数和分母阶数。

与式(1)相符合的差分方程如下:

图1 直接Ⅱ型结构IIR数字滤波器

3 MATLAB与IIR数字滤波器系数设计

MATLAB 软件提供了包括有 butter、ellip、cheby1、cheby2以及bessel等专用函数，在进行IIR滤波器设计时直接调用函数就可以设计出相应的低通、高通、带通或者带阻的滤波器。倘若设计保留200 Hz低频信号并滤除800 Hz高频信号的IIR滤波器，须先假设存在着混频信号S，则

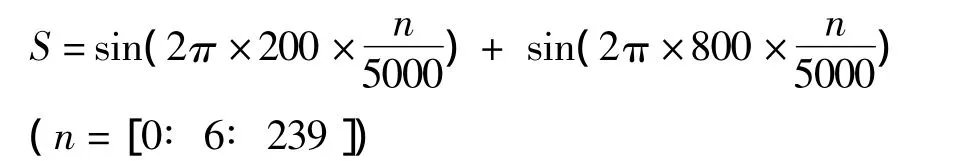
一般地，可在MATLAB软件中直接调用butter与buttord函数，就能实现巴特沃斯IIR滤波器的设计。在给定滤波器性能的基础上，通过buttord函数能求出相应的最小阶数n，并得到截止频率Wn。其中buttord函数式表示如下:

式(3)中，Wp、Ws与 Rp、Rs分别表示通带和阻带的截止频率与波纹系数，其 Wp、Ws∈［0，1］，若值为1 则表示为采样频率的。对混频信号进行滤波时，Wp=200/5000=0.04;Ws=800/5000=0.16;Rp=3 dB;Rs=40 dB。而butter的函数式用法如下:

式(4)中，n和Wn分别表示滤波器的阶数和截止频率，它们均是由buttord函数的式(3)所决定;butter函数所得到的系数是直接型滤波器系数，因此要运用dir2cas.m将其转换为级联型结构，其实现代码如下:

而在dir2cas文件中，其代码为:

在式(5)中，b0表示增益系数;B、A分别表示包含因子系数bk、ak的K行3列矩阵;a、b分别表示直线型分子、分母的多项式阶数。于是:

4 IIR数字滤波器的仿真实现

运用MATLAB软件的工具m文件，能实现IIR滤波器，其IIR.m源码如下:

function y=IIR(S，coefs)//S表示录入的混频信号，coefs表示系数矩阵，其排列方式为［a0，a1，a2，b0，b1，b2，…］

综上所述，将滤波器系数(采用上节通过MATLAB设计的系数)代入上述程序中，也就是说:

录入的混频信号S以及IIR数字滤波器的输出y的波形图如图2所示。

5 结束语

本文阐述了IIR数字滤波器的设计原理，并基于MATLAB软件通过程序设计的方式，实现了对滤波器系数的设计，同时编码了IIR.m文件对IIR数字滤波器的功能加以实现，并运用IIR.m文件实现了对实际的混频信号滤波仿真设计。但限于篇幅，并未运用MATLAB软件的sosfilt函数加以仿真结果验证。总而言之，通过对IIR数字滤波器的设计发现，其设计界面简便直观，能有效地降低工作量，满足当前人们对数字信号处理的需求。

图2 输入混频信号S及其滤波器输出y的波形图

［1］许金龙，苏武浔.IIR数字滤波器的FPGA仿真与实现［J］.信息化纵横，2009，(16):30-33.

［2］屈 星，唐 宁，严 舒，杨 白.基于FPGA的IIR数字滤波器的设计与仿真［J］.计算机仿真，2009，(08):304-307.

［3］张晓光，徐 钊.IIR数字滤波器的优化设计和DSP实现［J］.电子工程师，2006，(03):37-39.

［4］郝小江，唐 宇.IIR数字滤波器设计及DSP实现［J］.工业控制计算机，2008，(09):91-92.

［5］刘舒帆，张小虹，任姝婕.IIR数字滤波器在定点DSP中可实现性的仿真分析［J］.现代电子技术，2008，(19):119-122.

［6］袁 森，曾秋丽.Matlab7.1环境下IIR滤波器的设计与仿真［J］.电脑知识与技术，2013，(19):4499-4502.

［7］魏国华.IIR数字滤波器的FPGA实现［J］.今日电子，2003，(03):20-21.