考虑铁损时的感应电机节能控制

陈雪琴，王步来，高 响，高 鹏，季文彪，史晓永

(上海海事大学，上海 201306）

0 引言

三相交流异步电动机在现代工农业中被广泛使用，其耗电量占到整个工农业耗电量的大头。感应电机由于设计工艺的原因，一般在75%额定负载左右达到最大效率，在额定负载时接近最大效率，但轻载时则效率较低，因而感应电机特别是轻载时的能量优化有很大的潜力［1，2］。MATLAB/Simulink 是图形化的多技术领域系统仿真工具，它使用交互型方框图建模方式迅速建立系统仿真模型［3］。其电气系统模块库包含了电路、电力电子、电气驱动和电力系统等电工学中常用基本元器件和仿真模型，特别是含有专门的电机模块库，给电气系统的建模与仿真带来了极大方便。但是，该模块库所提供的异步电机仿真模型，忽略了实际电机中真实存在的铁损，用它来研究与效率有关的电机性能时，势必会降低仿真精度，也无法用于精确的异步电机矢量控制仿真研究［4］。此外，由于它属于电气模块参数设置比较复杂，仿真时与常规Simulinik模块间需接入电压、电流测量模块等中间接口模块，增加了仿真系统的复杂性，严重影响系统稳定性和仿真速度［5］。因此，需要建立一个能真实反映电机实际物理过程的异步电机仿真模型，并且易于实现，有较强的稳定性，还要尽可能多地提供电机内部各机电状态量的数值，以供仿真研究时使用。本文推导出两相静止坐标系下考虑铁损的异步电机动态数学模型，在MATLAB/Simulink平台上搭建异步电动机仿真模型，引用最优转差概念，运用到矢量控制中，建立最优效率矢量控制系统。

1 考虑铁损的电机模型

在建立异步电动机的动态数学模型时，不能忽略铁损，因为如果省去铁损将难以满足电动机调速性能的要求，同样会对损耗的研究结果带来很多误差［6］。本文给出了考虑铁损的异步电机数学模型，所得出的模型考虑了铁耗等效电阻随频率变化而变化的情况，验证了考虑铁损时异步电机的控制效果，在逼近异步电机的损耗实际情况上更进了一步，这也使后面的节能控制更加准确。稳态运行时异步电机的“T”型等效电路图中，表征铁芯损耗的电阻与激磁电感有并联和串联两种处理方式。为了便于分析，采用后一种方式，即铁芯损耗电阻与激磁电感串联，如图1所示。

图1 异步电机“T”型等效电路

在忽略空间磁动势谐波及铁芯饱和影响的前提下，考虑铁芯的异步电动机在两相同步旋转dq坐标系下的数学模型可用方程组来表示:

电压方程:

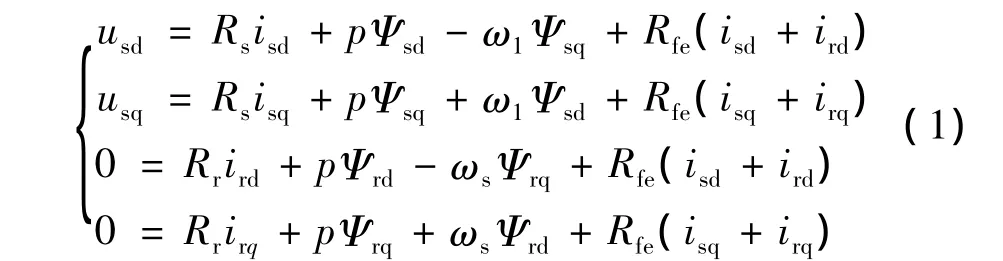
磁链方程:

转矩与运动方程:

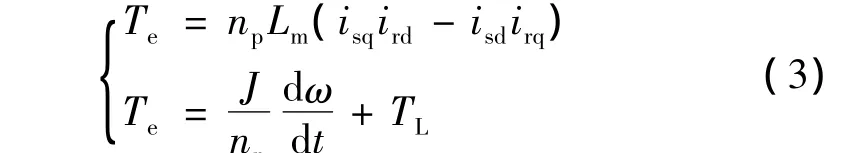
式中，主要符号物理意义如下:usd、usq为定子等效d轴和q轴绕组的电压;Ψsd、Ψsq为定子等效d轴和q轴绕组的磁链;isd、isq-定子等效 d 轴和 q轴绕组的电流;Rs、Rr、Rfe为定、转子绕组电阻和表征铁芯损耗的电阻;Ls、Lr、Lm为定、转子同轴绕组电感和互感(图1中的激磁电感);Lls、Llr为定、转子绕组漏感，其中 Ls=Lm+Lls，Lr=Lm+Llr;ω1、ω和ωs为同步旋转电角速度、转子旋转电角速度和转转差电角速度(转差角频率)，其中，ω1－ω =ωs，ω =dθ/dt，θ为d轴领先A相轴的电角度;np、p为电机极对数、微分算子;Te、TL为电机的电磁转矩及负载转矩;J为电机系统的转动惯量;Ψrd、Ψrq为转子等效d轴和q轴绕组的磁链;ird、irq为转子等效d轴和q轴绕组的电流;根据公式ΔPfe=≈ΔPfeN，可在空载情况下求出

2 异步电机节能控制

通过坐标变换，将异步电机在同步旋转坐标系下进行建模，探索转差频率与异步电机运行效率之间的内在联系，经过数学关系式推导，引用了最优转差的概念，即在异步电机运行时，在负载转矩合理的范围内，存在着某一转差频率，使电机的运行效率始终达到最高。在此理论基础上，结合了传统稳态转差频率控制系统，建立了基于异步电机转差频率的最优效率控制系统。此系统在轻载时节能空间较大，结构简单，但动态性能较差。因此，本文将最优转差的思想推广到了矢量控制，提出了一种异步电机最优效率矢量控制系统，此系统在保证转差频率始终维持在最优转差的前提下，重新解耦异步电机转矩电流分量和励磁电流分量，从而在保证异步电机运行效率最高的基础上进行动态控制。

在忽略铁损的情况下，可得到效率的表达式:

此时为求最优效率，将上式效率对转差角频率求偏导并令其等于零，求得效率最高时对应的最优转差角频率:

考虑铁损时候的效率公式为:

与此对应的最优转差角频率则为:

基于最优转差角频率的异步电机矢量控制系统控制框图如图2所示。

图2 异步电机最优转差频率控制系统

异步电机最优转差频率控制系统，是将最优转差控制策略运用到矢量控制系统中，系统中的转差频率直接给定，为最优转差，并以此为前提去分解转矩电流和励磁电流，因此异步电机最优转差频率控制系统可以在保证异步电机运行效率最大的前提下进行动态控制。

3 仿真实例

本文在MATLAB7.0环境下采用考虑损耗模型控制法进行了节能控制仿真，根据图2原理图可以搭建出仿真模型如图3所示。输入电动机的基本参数为:Rr=1.225 Ω，Rs=1.337 Ω，Lr=0.1161 H，Ls=0.11356 H，Rfe=0.2106 Ω，额定功率为 1.5 kW，极对数为2，基频为50 Hz，每相基压为127 V。当负载为 1 Nm时，其仿真波形如图4所示。

图3 考虑损耗的仿真模型

图4 考虑铁芯损耗时的转速、转矩、定子电流波形

利用图3的仿真模型，通过在不同转速下，电机分别运行在转速300 r/min、450 r/min，带动负载转矩2 Nm，4 Nm，7 Nm，计算其运行效率，如表1。

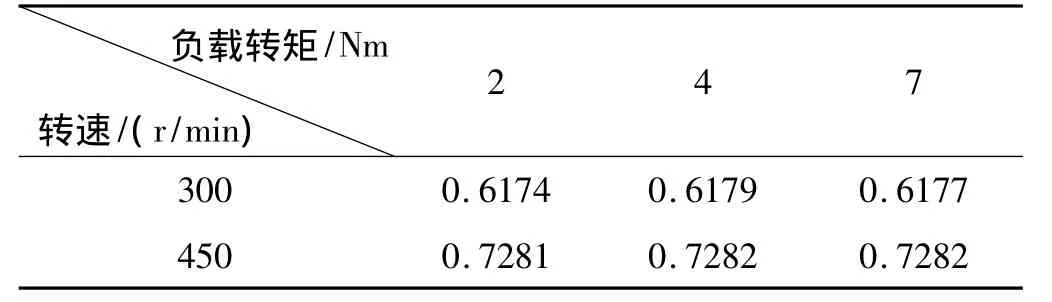
表1 考虑铁损时的异步电动机最优转差频率控制系统效率表

当不考虑铁芯损耗时，在相同转矩条件下建立异步电机转差频率控制系统效率数据如表2。

表2 异步电动机转差频率控制系统效率表

由上述数据可见，考虑铁损时的最优转差频率控制在轻载时的节能效果较好，在系统转速和转矩不变的情况下，该方法比传统的转差频率控制方法可提高效率8%左右，然而随着负载转矩的增大，节能空间也相应的递减，通过更多的仿真实验可得，当异步电动机在额定负载转矩附近，其节能空间很小，在轻载时节能空间较大。

4 结束语

本文建立在d-q坐标系下考虑铁损的异步电动机动态数学模型，在此数学模型基础上从动态和稳态两方面验证了模型的正确性，把电机节能控制与考虑铁损的矢量控制有机结合起来，并给出该仿真模型的电动机运行情况，同时也验证了铁损是异步电动机不可忽略的一部分，尤其对于研究异步电机效率优化控制具有现实意义。

本文在Simulink平台上实现了考虑铁损的异步电机模型，并在此基础上建立了基于最优转差频率的节能控制，建立了总损耗的模型，并利用Simulink对采用节能考虑铁损的控制策略系统与不带节能且不考虑铁损的系统作了仿真对比实验。

［1］FLEMMIMG Abraharnser.Energy optimal control of induction motor drive［D］.Aalborg University:Institute of Energy Technology，2000.

［2］ALEXANDER Kusko，DONALD Galler.Control means for minimization of losses in AC and DC motor drives［J］.IEEE Trans.Ind.Application，1983，19(4):561-570.

［3］王宏华.开关型磁阻电动机调速控制技术［M］.北京:机械工业出版社，1995.

［4］纪良文.开关磁阻电机调速系统及其新型控制策略研究［D］.杭州:浙江大学，2002.

［5］芦晓静，温旭辉，张立伟，陈桂兰.考虑铁损的异步电机仿真建模.［J］.电机与控制应用，2005，132(8):3-6.

［6］李穗冬，童建平.基于模型的矢量控制异步电机效率优化控制研究［J］.微计算机信息，2008，5(1):35-36.