三角代数上导子的两个结论
李 霞,孙成侠,马 晶
(吉林大学 数学学院,长春130012)
设R是有单位元的交换环,A,B都是R上的酉代数,M是一个非零(A,B)-酉双模,则形式矩阵的集合
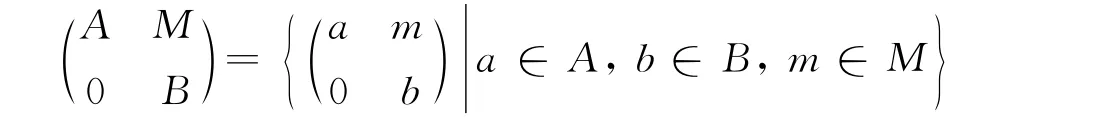
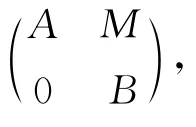
如果对任意的x,y∈A都有d(xy)=d(x)y+xd(y),则R-代数A 的R-线性映射d:A→A称为A的导子.记[y,x]=yx-xy.若特征非2的素环R上有非零导子d满足[d(x),d(y)]=0,∀x,y∈R,则R是交换的[5].本文基于文献[5]讨论三角代数T满足广义恒等式[D(X),D(Y)]=0导子的结构.则T称为三角代数[1-4].本文记若环R的映射f在其子集S 上满足[f(x),f(y)]=[x,y],∀x,y∈S,则称f在S 上是强保交换的[6].若素环R的导子在其非零右理想上是强保交换的,则R是交换的[6].若素环R的导子在其非零右理想U 上是强保交换的,则U⊆Z(R)(Z(R)是R的中心)[7].设Γ=Tri(A,M,B)是三角矩阵环,Φ是Γ上的满射,齐霄霏等[8]证明了:在适当条件下,如果Φ在Γ上是强保交换的,则存在Γ到其中心Z(Γ)的映射μ及λ∈Z(Γ),使得λ2=1Γ,并且对任意的X∈Γ有Φ(X)=λX+μ(X).本文将证明三角代数T的导子都不是强保交换的.
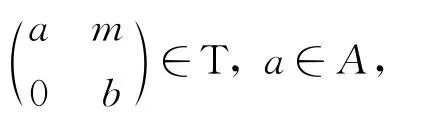
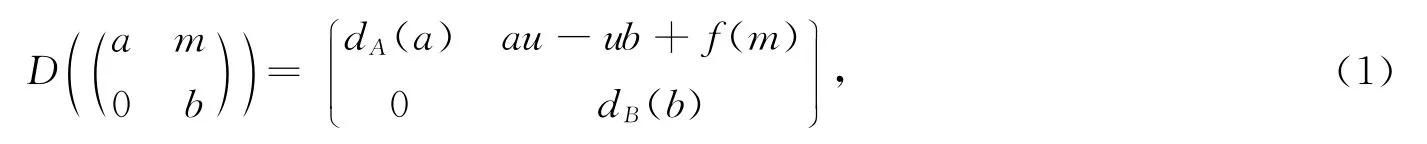
且f满足
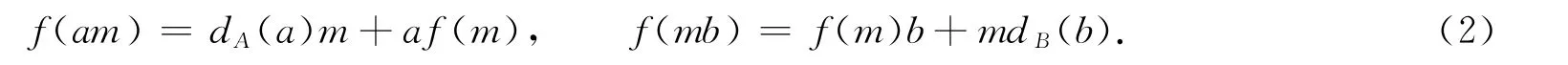

证明:对任意的a,c∈A,b,d∈B,x,y∈M,有

其中

设D 在T上满足[D(X),D(Y)]=0.由式(3)可知
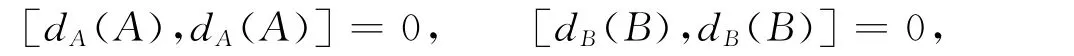
并且对任意的a,c∈A,b,d∈B,x,y∈M,有
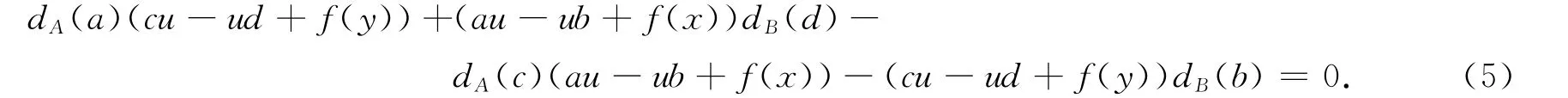
式(5)中取a=0,x=y=0,得
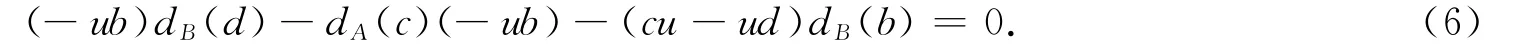
式(5)中取a=1,x=y=0,得
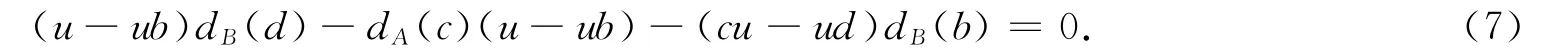
式(7)减式(6)得udB(d)-dA(c)u=0,c∈A,d∈B.分别取d=1,c=1得dA(A)u=udB(B)=0.取a=aα,b=bβ,α∈A,β∈B,得dA(A)Au=uBdB(B)=0,则式(4)可化简为
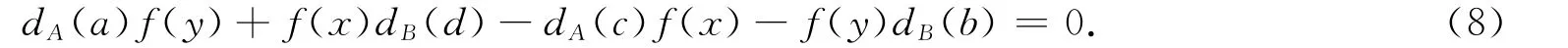
式(8)中取y=0,c=0,得
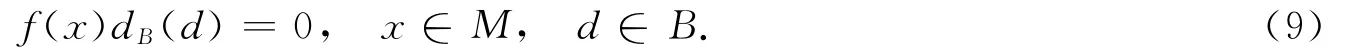
取d=βd,β∈B,可得f(M)βdB(B)=0.于是,式(9)中取x=xβ,β∈B,并利用式(2)可得MdB(β)dB(d)=0,对任意的d,β∈B 都成立.由 M 的忠实性可得dB(B)2=0.同理,在式(8)中取y=0,d=0可得dA(c)f(x)=0,c∈A,x∈M.取c=cα,α∈A,可得dA(A)Af(x)=0.于是在dA(c)f(x)=0中取x=αx,α∈A,并利用式(2)可知,对任意的a,c∈A 都有dA(c)dA(α)M=0.又因为M 是忠实的,所以dA(A)2=0.
反之,当dA(A)2=0,dB(B)2=0时,显然有[dA(A),dA(A)]=0并且[dB(B),dB(B)]=0.由dA(A)u=0可知,对任意的x,y∈A 有dA(xy)u=0,从而dA(A)Au=0.同理,由udB(B)=0可得uBdB(B)=0.将dA(A)Au=0,uBdB(B)=0和dA(A)f(M)=f(M)dB(B)=0代入式(4)可知Δ=0,从而由式(3)可知D 在T上满足[D(X),D(Y)]=0.
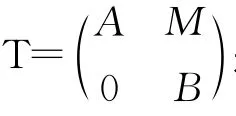
证明:设D是T的导子并且在T上强保交换,则对任意的a,c∈A,b,d∈B,x,y∈M,有
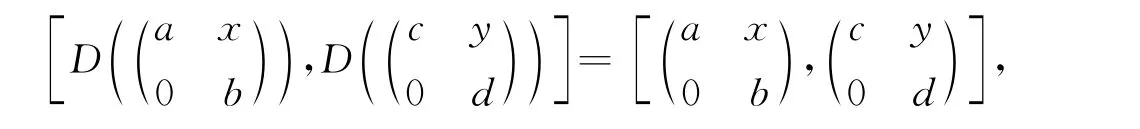
设D形如式(1),则
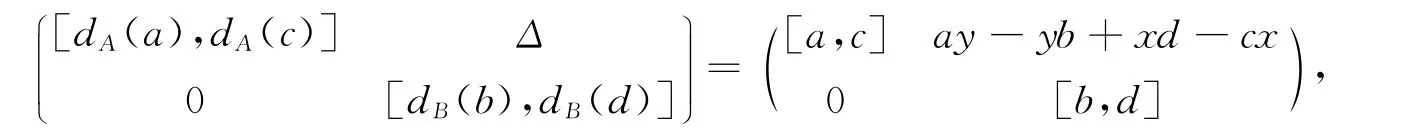
其中Δ形如式(4).因此
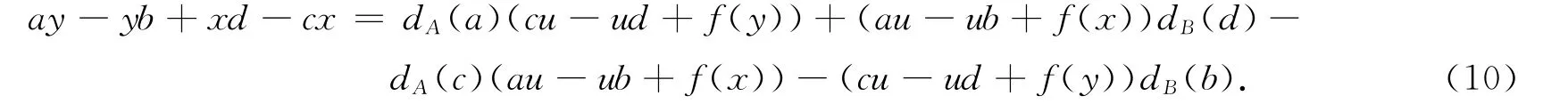
式(10)中取a=0,x=0,得
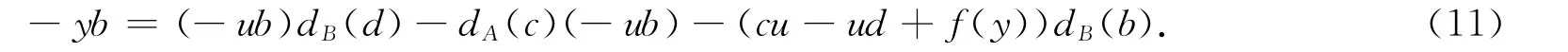
式(10)中取a=1,x=0,得
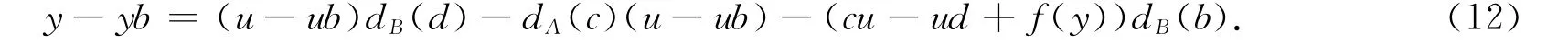
式(12)减式(11)可得:对任意的y∈M,c∈A,d∈B 都有y=udB(d)-dA(c)u.取c=0,d=0可得y=0.由y的任意性可知M=0,这与三角代数的定义矛盾,故三角代数T的导子都不是强保交换的.
[1]HAN Dong,WEI Feng.Jordan (α,β)-Derivations on Triangular Algebras and Related Mappings[J].Linear Algebra Appl,2011,434(1):259-284.
[2]Chase S U.A Generalization of the Ring of Triangular Matrices[J].Nagoya Math J,1961,18:13-25.
[3]Harada M.Hereditary Semi-primary Rings and Tri-angular Matrix Rings [J].Nagoya Math J,1966,27:463-484.
[4]Haghany A, Varadarajan K.Study of Formal Triangular Matrix Rings [J].Comm Algebra,1999,27(11):5507-5525.
[5]Hersterin I N.A Note on Derivations[J].Canad Math Bull,1978,21(3):369-370.
[6]Bell H E,Mason G.On Derivations in Near-Rings[J].North-Holland Math Studies,1987,137:31-56.
[7]Bell H E,Daif M N.On Commutativity and Strong Commutativity-Preserving Maps[J].Canad Math Bull,1994,37(4):443-447.
[8]QI Xiaofei,HOU Jinchuan.Strong Commutativity Preserving Maps on Triangular Rings[J].Oper Matrices,2012,6(1):147-158.
[9]谢乐平,曹佑安.形式三角矩阵环的导子和自同构 [J].数学杂志,2006,26(2):165-170.(XIE Leping,CAO Youan.Derivations and Automorphisms of Formal Triangular Matrix Rings [J].J Math,2006,26(2):165-170.)

