降能片对12C6＋束流影响的Geant4模拟

易海云，赵广义，王明勇，马玉刚，王振超，周 庆，李 建，王 健

（1.吉林大学 物理学院，长春130012；2.鞍山师范学院 物理系，辽宁 鞍山114005；3.黑龙江省科学院 技术物理研究所，哈尔滨150086；4.天津市技术物理研究所，天津300192；5.吉林大学 学报编辑部，长春130012）

随着重离子加速器的发展，利用重离子治疗肿瘤得到迅速发展，其中碳离子束具有倒转深度剂量分布（Bragg peak）和较高相对生物学效应（REB）等特点，在治疗癌症中应用广泛.束流主动型配送系统［1］或束流扩展被动型束流配送系统［2］均有变能装置——降能片对肿瘤实施适形放射治疗.本文通过Monte Carlo方法模拟计算12C6＋束流经降能片后的束流分布特性，并讨论束流能量、降能片材料和厚度对12C6＋束流角度歧离、能量歧离及Bragg峰的影响.

1 计算方法与模型

利用Geant4获取每核子能量在80～360MeV内碳离子穿过质量厚度为0.5～4.0g／cm2的有机玻璃（PMMA）、铝（Al）、铜（Cu）和铅（Pb）4种靶材降能片后的角分布和能量分布数据及碳离子在水中的Bragg峰数据.先利用Origin9.0对数据进行处理，再将处理结果与理论计算值进行比较，并分析12C6＋能量、降能片材料及质量厚度对12C6＋束流的影响及降能片质量厚度对Bragg峰的影响.

本文所用模型的几何示意图如图1所示，其中：世界体为一个真空的立方体盒子；降能片为一个长和宽相等，高可根据实验要求变化的长方体盒子，其内部填充物由实验所需靶材确定.测量歧离时，探测器内未填充任何物质，其形状与功能由测量目的确定［3］；测量碳离子束的Bragg峰时，探测器内的填充物质为水，其形状为一个与降能片长和宽相等、高大于对应碳离子平均自由射程的长方体.

图1 模型的几何示意图Fig.1 Geometrical sketch map of model

2 角度歧离

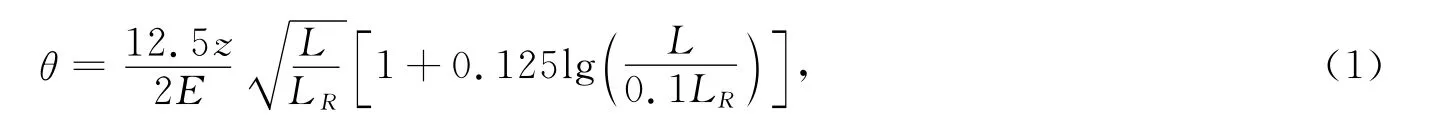
其中：z为入射粒子的电荷数；E为入射粒子的动能；L和LR分别为散射体的质量厚度和辐射长度［10］.

2.1 角度歧离值θ随12C6＋能量和靶材的变化规律

将靶质量厚度固定为0.5g／cm2，改变碳离子的能量和靶材，其角度歧离值θ随碳离子能量和靶材的变化关系如图2所示.由图2可见：

1）模拟曲线与理论曲线几乎重合，在最上面2条曲线的末端偏离最大，即360MeV碳离子穿过Pb靶处，误差值为10.12%，该误差值可以接受（修正过的Highland公式，精确度为11%［6］）.

2）当降能片材料一定时，θ随碳离子能量的增加而减小；当碳离子能量一定时，θ随靶材原子序数的降低而减小，即角度歧离程度随碳离子能量的增加和靶原子序数的降低而减小.

3）随着碳离子能量的增加，各种靶材θ值间的差距越来越小，即角度歧离程度受靶材的影响随碳离子能量的增加而减小.

2.2 角度歧离值θ随靶质量厚度及靶材的变化规律

将碳离子能量固定为160MeV，改变靶质量厚度及靶材，其θ随靶质量厚度及靶材的变化关系如图3所示.由图3可见：

1）模拟曲线与理论曲线几乎重合，其偏离程度随靶质量厚度的增加而增大，且化合物靶比单质靶更明显.Pb，Cu，Al，PMMA靶模拟值与理论值间的最大误差分别为5.18%，6.63%，6.64%，29.65%，其中PMMA误差较大是因为其为化合物，且所选靶质量厚度大于PMMA厚度（靶厚与薄根据各自的模型确定［5］），导致PMMA的θ计算公式与式（1）不同［6］.

图2 θ随12C能量及靶材的变化关系Fig.2 Changes ofθwith the energy of 12C and the material of target

图3 θ随靶质量厚度及靶材的变化关系Fig.3 Changes ofθwith the mass thickness and material of target

2）当靶材一定时，θ随靶质量厚度的增加而增大，但角度歧离最大值小于1.1°，即角度歧离的程度较小.

转发锦鲤的背后，是人们对吉祥欢乐、好运的向往，尽管只有千万分之几乃至更低的中奖几率，这种人性的需求是不会过时的。此外，转发一条企业的相关微博，并不需要很高的成本，也不需要花费很多的时间成本，因此即便是小概率的中奖几率，加上锦鲤的寓意以及吸引力极强的礼单，使得人们都抱有试一试的心态，是一种“高投机性行为”。

3）随着靶质量厚度的增加，各种材料靶间的θ值差距越来越大，即角度歧离程度受靶材的影响随靶质量厚度的增加而增大.

综上，碳离子能量越高，靶材原子序数越低、靶质量厚度越小时，角度歧离程度越小.

3 能量歧离

在入射粒子穿过靶物质过程中，与靶核发生多次碰撞而导致其能量损失.该能量损失歧离可用Gauss分布描述［11－13］，即用Gauss分布的均方差参数σ描述能量歧离程度的大小.目前，关于能量歧离的研究成果较多［4，14－18］，本文理论计算利用Bohr公式，即

式（2）为Gauss制下的公式，为方便计算，将σ的单位换为MeV，将靶的厚度t改为质量厚度，并用一个系数表示公式中的常量，将式（2）变为

其中：z为入射粒子的原子序数；Z和A分别为靶的原子序数与原子质量；x为靶的质量厚度.

3.1 能量歧离值σ随碳离子能量和靶材的变化关系

将靶质量厚度分别固定为0.5g／cm2和4.0g／cm2，改变能量和靶材，其能量歧离与束流能量及靶材间的关系如图4所示.

图4 能量歧离与能量及材料的关系曲线Fig.4 Relational curves of energy straggling with energy and target

由图4可见：

1）所有靶的模拟曲线均在其理论曲线上方，即模拟值大于理论值，这是因为理论计算仅考虑了电子相互作用对能量损失歧离值的影响，而忽略了核相互作用和离子电荷交换作用所致.

2）理论曲线为一条平行线，即理论认为能量歧离值与入射碳离子的能量无关，但模拟曲线表明能量歧离值随碳离子能量的变化而变化，当靶质量厚度由0.5g／cm2变为4.0g／cm2时，能量歧离值随靶质量厚度的变化规律相反，即在近似条件下，能量歧离值与束流能量无关.

3）当靶的质量厚度一定时，能量歧离值随靶原子序数的增加而降低，且随靶材Z／A的变化而变化.

3.2 能量歧离值σ随靶质量厚度及靶材的变化关系

当碳离子能量为每核子320MeV时，改变靶材及靶质量厚度，其能量歧离值与靶质量厚度及靶材的关系如图5所示.由图5可见：

1）模拟曲线与理论曲线随靶质量厚度的变化趋势一致，模拟曲线均在理论曲线上方，即模拟值大于理论值.

2）当靶材一定时，能量歧离值随靶质量厚度的增大而增大；当靶质量厚度一定时，能量歧离值随靶原子序数的减小而增大.

3）随着靶质量厚度的增加，各种靶材料能量歧离值间的差距随靶材原子序数间差距的增加而增大，表明靶质量厚度越大，能量歧离值受靶原子序数的影响越大.

综上，能量歧离值随靶质量厚度的增加及靶材Z／A的增大而增大，在近似条件下，能量歧离值与碳离子能量无关.

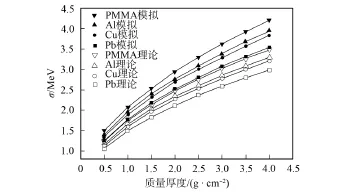
图5 能量岐离与靶质量厚度及靶材的关系曲线Fig.5 Relational curves of energy straggling with the mass thickness and material of target

4 降能片对Bragg峰的影响

给出两组对比实验数据：一组是碳离子穿过靶后再进入水中的Bragg峰数据，即碳离子进入水前的能量满足Gauss分布，另一组是碳离子直接进入水中的Bragg峰数据，即碳离子进入水前的能量是第一组实验Gauss分布中心峰位的能量值，是单能的.

将PMMA作为降能片，当碳离子能量为160MeV时，改变降能片厚度，其Bragg峰如图6所示.

图6 PMMA靶对Bragg峰的影响随靶质量厚度的变化关系Fig.6 Effect of PMMA target on Bragg peak with the change of mass thickness of target

由图6可见，2个峰高度和宽度间的差异随降能片厚度的增加而增大，其中一个峰的高度降低、宽度增大，另一个峰变尖锐.即降能片对Bragg峰的影响随靶质量厚度的增加而增大.

综上可见，碳离子能量越高，降能片质量厚度越小，12C6＋束流经降能片后的角度歧离和能量歧离值越小，其Bragg峰受降能片的影响也越小.

［1］Haberer T，Becher W，Schardt D，et al.Magnetic Scanning System for Heavy Ion Therapy［J］.Nucl Instr and Meth in Phy Res Sec A，1993，330（1／2）：296－305.

［2］Kanai T，Endo M，Minohara S，et al.Biophysical Characteristics of HIMAC Clinical Irradiation System for Heavy－Ion Radiation Therapy［J］.Int J Radiat Oncol Biol Phys，1999，44（1）：201－210.

［3］YANG Hai－fang.Monte Carlo Simulation of the Angle and Energy Straggling of Proton in Thin Target［D］.Changchun：Jilin University，2011.（杨海芳.质子打薄靶的角度和能量歧离的蒙特卡罗模拟 ［D］.长春：吉林大学，2011.）

［4］复旦大学，清华大学，北京大学.原子核物理实验方法 ［M］.2版.北京：原子能出版社，1985：59－60.

［5］Frühwirth R，Liendl M.Mixture Models of Multiple Scattering：Computation and Simulation ［J］.Computer Physics Communications，2001，141（2）：230－246.

［6］Lynch G R，Dahl O I.Approximations to Multiple Coulomb Scattering［J］.Nucl Instr and Meth in Phy Res Sec B，1991，58（1／2）：6－10.

［7］Gottschalk B，Koehler A M，Schneider R J，et al.Multiple Coulomb Scattering of 160MeV Protons［J］.Nucl Instr and Meth in Phy Res Sec B，1993，74（4）：467－490.

［8］QIAO Song－lin.The Numerical Simulation ofα Particles Transport ［D］.Mianyang：China Academy of Engineering Physics，2005.（乔松林.α粒子输运的数值模拟 ［D］.绵阳：中国工程物理研究院，2005.）

［9］Highland V L.Some Practical Remarks on Multiple Scattering ［J］.Nucl Instr and Meth，1975，129（2）：497－499.

［10］TSAI Yung－su.Pair Production and Bremssthrahlung of Charged Leptons ［J］.Rev Mod Phys，1974，46（4）：815－851.

［11］Yang Q，Li T R，O’Connor D J，et al.Energy Loss Straggling of MeV12C and16O Ions in Carbon［J］.Nucl Instr and Meth in Phy Res Sec B，1993，83（4）：439－448.

［12］Eckardt J C，Lantschner G H.Experimental Energy Straggling of Protons in Thin Solid Foils［J］.Nucl Instr and Meth in Phy Res Sec B，2001，175／176／177：93－97.

［13］Msimanga M，Pineda V C A，Comrie C M，et al.Heavy Ion Energy Loss Straggling Data from Time of Flight Stopping Force Measurements［J］.Nucl Instr and Meth in Phy Res Sec B，2012，273：6－10.

［14］Yang Q，O’Connor D J，WANG Zhong－lie.Empirical Formulae for Energy Loss Straggling of Ions in Matter［J］.Nucl Instr and Meth in Phy Res Sec B，1991，61（2）：149－155.

［15］Weick H，Sφrensen A H，Geissel H，et al.Energy－Loss Straggling of（200—1 000）MeV／u Uranium Ions［J］.Nucl Instr and Meth in Phy Res Sec B，2002，193（1／2／3／4）：1－7.

［16］Geissel H，Weick H，Scheidenberger C，et al.Experimental Studies of Heavy－Ion Slowing Down in Matter［J］.Nucl Instr and Meth in Phy Res Sec B，2002，195（1／2）：3－54.

［17］Diwan P K，Sharma V，Kumar S，et al.Energy Loss and Straggling of MeV Heavy Ions in Polypropylene Absorber Foils［J］.Nucl Instr and Meth in Phy Res Sec B，2007，258（2）：293－298.

［18］Diwan P K，Kumar N S.Energy Loss Straggling in Different Polymeric Foils forα－Particles ［J］.Radiation Physics and Chemistry，2012，81（10）：1543－1546.