基于中心自动融合的多尺度可能性聚类算法

胡雅婷，左春柽，曲福恒

（1.吉林农业大学 信息技术学院，长春130118；2.吉林大学 机械科学与工程学院，长春130022；3.长春理工大学 计算机科学技术学院，长春130022）

聚类分析是一种以数据间的相似性为基础将未标记数据划分到不同的类别，从而获得数据中的结构分布模式方法，在数据挖掘、图像处理及人工智能等领域应用广泛［1］.聚类算法主要分为硬聚类与模糊聚类［2－3］两类.由于模糊聚类方法考虑到样本点与各类别间的联系，聚类结果较硬聚类更客观，因此已成为聚类分析研究的主流.Krishnapuram等［4－5］在模糊聚类的基础上提出了可能性c－均值（PCM）聚类算法，PCM算法中的隶属度值代表样本属于各类别的绝对可能性，有效地避免了模糊聚类算法对噪声和野值敏感的问题.但PCM算法易于产生重合聚类，并对初始化中心和参数设置非常敏感，作为一种模式搜索算法，当选取的初始聚类中心个数与数据模式个数不等时，PCM算法将不能自动搜索到数据中的所有模式.即使二者相等，多个初始点选取的位置不当也可能导致算法搜索到相同模式，即产生重合聚类问题［5－6］.而以每个数据为初始中心进行搜索又会加大计算量，也会影响目标函数对真正模式位置的搜索.中心自动融合机制［6］是为了解决参数选择和初始化问题而提出的，以所有的数据点作为初始模式，根据原始的数据结构自组织聚类结构，有效解决了PCM算法中存在的问题.

自然界中多数数据集合都具有不同尺度的聚类结构，即在较大类别中还包含了较小类别的嵌套结构.为能分离出不同的类别结构，识别出类别间的交叉点，保证类别的光滑连续性，尤其能够识别出通过交点的不同类别［7］，需要设计一种适用于具有多种尺度结构数据集合的有效聚类算法.本文通过在原始可能性聚类中引入多尺度因子控制聚类的尺度，采用自动融合机制自动搜索聚类模式并确定聚类数目，提出一种基于中心自动融合的多尺度可能性（multi－scale possibilistic clustering algorithm based on automatic center merging，MPC－ACM）聚类算法.MPC－ACM算法根据数据集合的结构特点自适应地组织聚类结构，并自动确定聚类数目，且算法中的多尺度因子还可获得不同尺度下的聚类划分.多尺度因子的引入增加了算法的可控性与灵活性，使其具有更广的使用范围，并从理论上给出多尺度因子的多尺度性质证明，最后在人造数据集和滚动轴承故障数据上进行实验分析.

1 可能性聚类算法

设由n个数据点构成的数据集合X的c－划分可表示为一个c×n阶矩阵U＝（uij），其中c为聚类个数.对应于集合X，可能性聚类、模糊聚类与硬聚类产生的c－划分空间分别由下式表示［8］：

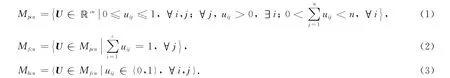
通过最小化目标函数JPCM获得PCM聚类模型［4－5］：

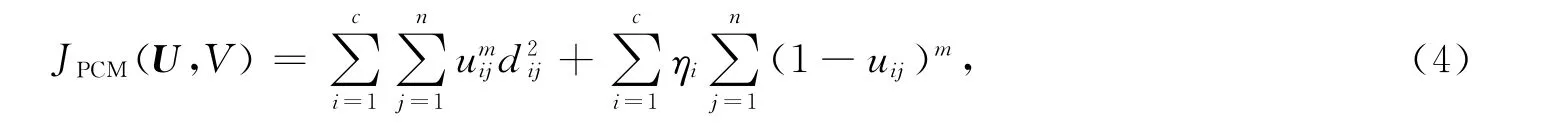
得到满足最优解的两个必要条件：

将式（5）和式（6）迭代直至收敛得到满足式（4）的一个（局部）最优解.其中：U＝（uij）表示可能性划分矩阵；V＝｛v1，v2，…，vc｝⊂ℝs表示聚类模式（中心）集合；c表示聚类数目；m表示模糊系数；ηi表示需要用户定义的参数.PCM算法的隶属度值表示样本属于各类别的绝对可能性，可较好抑制噪声产生的影响.但算法存在易于产生重合聚类的不足，并对初始化模式（中心）及参数ηi非常敏感.

2 MPC－ACM 算法

2.1 中心自动融合机制

MPC－ACM算法对具有较高相似度的中心按设定的准则进行自动融合，这种自动融合机制［6］将全体模式作为初始的搜索点（初始化聚类中心），在迭代过程中动态地改变聚类个数与聚类结构.在某个迭代中，若当前两个搜索点的相关性非常高，则认为这两个搜索点来源于同一个聚类，将其进行合并操作，其中关键是相关度的确定.本文采用文献［6］的方法，根据两个点属于其他所有聚类隶属度向量的相关性定义其相关度大小.

设U＝（uij）c×n＝（u1，u2，…，uc）T，R＝（ril）c×c表示相关性矩阵，则有

类的合并准则建立在相关系数矩阵R上.令S＝｛S1，S2，…，Sc｝，其中

由Si的定义可见，它体现了所有聚类中心点与第i个中心vi间的相似程度，如果各中心与vi的距离较近则Si的值较大.因此，Si在一定程度上反映了vi周围数据点的密度.合并操作由密度最大的中心开始，先按各类Si值的大小排序，找到最大值对应的中心vi，其他所有与vi相似度大于ρ的中心合并为一类.设I表示未合并数据的指标集合，令

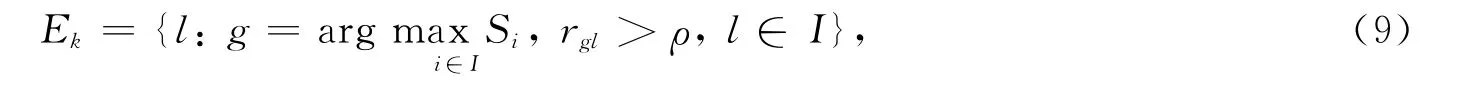
这里

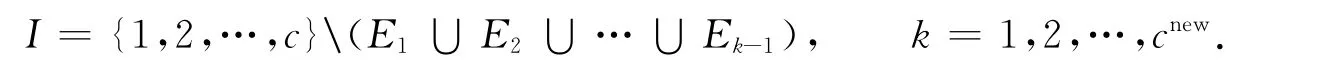
Pc为第c个聚类所有数据形成的集合.由于合并会导致类内数据的增加，因此需要对发生合并的类中心进行修正，合并后新的聚类中心按下式计算：

本文称这种中心自动融合机制下的算法为合并算法（merging algorithm，MA），步骤如下：

1）令k＝1，I＝｛1，2，…，c｝；

2）根据式（7）更新R；

3）根据式（8）更新S；

4）根据式（9）更新Em；

5）令I＝I＼Em，如果I≠Ø，则令k＝k＋1，返回4）；否则，更新cnew＝k；

6）根据式（10），（11）更新Pnew和Vnew，算法结束.

2.2 MPC－ACM算法流程

为使MPC－ACM算法不仅能对初始化与参数具有较强的鲁棒性，而且同时具有对数据的聚类结构进行多尺度分析能力.本文在已有可能性聚类算法PCM中引入一个多尺度因子，通过调节多尺度因子获得不同大小的聚类结构.同时，采用自动融合机制进行模式搜索和聚类数目自动确定，算法实现步骤如下：

1）设置ε，η值，其中ηc＝（η，…，η）1×c；

2）初始化k′＝0，V（0）＝X，U（0）＝f（η，V（0），X）；

3）先根据U（k）找出V（k′）中相关性大于ρ的中心，利用MA算法对这些中心合并，再根据式（11）对合并后的中心进行修正得到Vnew；先利用Vnew与式（6）更新U（k′＋1），再利用U（k′＋1）与式（5）更新V（k′＋1）；

4）如果‖V（k′＋1）－V（k′）‖＜ε，则停止；否则，返回3），令k′＝k′＋1.

2.3 多尺度性质

在原始可能性聚类中，ηi与聚类大小相关，用于识别不同体积的聚类.本文MPC－ACM算法中假设ηi为常数，即ηi＝η（i＝1，2，…，c）.通过调节η的值，MPC－ACM 算法可得到不同尺度下的聚类结构，本文称η为多尺度因子.

定理1 设m＞1，ρ∈（0，1），则当η→0＋时，MPC－ACM算法得到数据的最小尺度聚类结构，即每个模式自身为一类.

证明：假设X＝｛x1，x2，…，xn｝⊂ℝs中数据不存在重复现象，即当j1≠j2时，必有xj1≠xj2.MPC－ACM算法的初始搜索点是数据集合中的任意一点，式（5）表明，当η→0＋时，对任意给定的1≤j≤n，当i≠j时，uij＝0；当i＝j时，uij→1.MPC－ACM算法中的rij→0（i≠j），此时必有rij＜ρ，根据MA算法可知，不会对任何两个中心进行合并操作.式（6）表明，中心xj将更新为x′j，且两者必然满足‖xj－x′j‖＜ε.根据MPC－ACM算法的终止条件可知，算法此时停止.由于没有进行任何合并操作，因此每个模式自身必然为一类.若有重复数据，可先把重复数据合并为一个数据得到同样的结果，证毕.

定理2 设m＞1，ρ∈（0，1），则当η→＋∞时，MPC－ACM算法得到数据的最大尺度聚类结构，即所有模式分为一类.

证明：当η→＋∞时，式（5）表明uij→1（∀i，j），又由式（7）可知rij→1（∀i，j）.ρ是一个常值，且满足ρ＜1.由MA算法可知，所有的模式即初始化的聚类中心将被合并为一类，证毕.

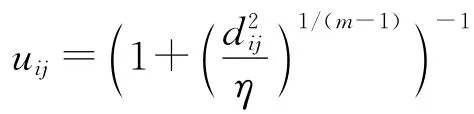
定理1和定理2也表明了MPC－ACM算法的多尺度性质.文献［9］中MPCM算法的多尺度性质来源于均值漂移聚类的带宽控制，可能性聚类具有辅助调整最终聚类中心的作用；本文MPC－ACM算法的多尺度性质由可能性聚类本身的多尺度因子控制.MPCM算法由于采用了均值漂移聚类，其计算复杂度较高，网格剖分的引入虽然会减少初始迭代中心个数，降低计算复杂度，但同时会降低聚类精度.即使在不引入网格剖分的前提下，MPC－ACM算法由于在迭代过程中的中心个数会逐渐减少，必然具有效率优势，且MPC－ACM算法同样可采用完全相同的“利用网格剖分减少初始迭代点的技术”降低计算复杂度.因此，MPC－ACM算法比MPCM算法更高效.

3 实验结果及分析

3.1 人造数据实验

图1为不同聚类算法在具有不同大小聚类结构数据集合上的聚类结果.由图1可见：FCM算法由于对初始化的依赖性较高导致其很难发现正确的聚类结果，即使FCM算法的初始化中心是正确的，也无法得到真正不同大小的聚类结构，且FCM算法的初始化中心如何选取目前仍没有合理方法；PFCM算法与FCM算法类似，由于初始化的敏感性导致错误的聚类划分；PCM算法的聚类结果也严重依赖于初始化中心的选择，如图1（D）所示PCM算法还存在容易产生重合聚类的问题，但算法的模式搜索性质使其正确的确定了4个类中心位置；UPC算法受到初始化、产生重合聚类的影响，其结果最不理想，算法不具备模式搜索性质，产生两组重合聚类的聚类中心位置与实际偏差较大；本文提出的算法获得了正确的聚类划分.

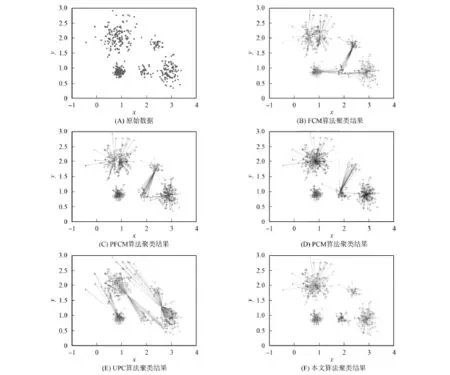
图1 不同尺寸与个数的数据集聚类结果Fig.1 Clustering results on set of different size and number

下面测试本文算法的多尺度性质.实验数据集具有如图2（A）所示的多尺度聚类结构，第一级尺度为左右2类，第二级尺度为左上、左下、右上和右下4类，第三级尺度为12个小类.如图2（B）～（F）所示，当多尺度因子η由大至小逐渐变化时，算法能逐级找到不同尺度下的聚类结构，这也验证了定理1和定理2.如定理2所述，当尺度因子充分大时，所有数据将被划分为一类.如图2（B）所示，当η≥10×θ（X）时，所有数据被划分到同一类中.如定理1所述，当尺度因子充分小时，每个不同的数据分为一类.如图2（F）所示，当η≤0.01×θ（X）时，每个数据独立成为一类.因此，尺度因子可控制算法得到的聚类尺度.

3.2 真实数据实验

实验数据源于美国凯斯西储大学电气工程实验室采集的6205－2RS JEM SKF深沟球轴承数据［12］.分别选取在正常、内环故障、滚动体故障情况下样本各473个和外环故障情况下样本474个.轴承上所有类型的故障均为由电火花加工的单点损伤，其中直径为0.177 8mm和0.533 4mm的故障状态分别对应轻微和严重故障.在故障特征提取阶段，首先对数据进行EMD分解，对其IMF1分量［13］进行统计分析，计算其裕度系数、均方根、波形因子、峰值、峭度及脉冲因子值组成的六维特征矢量.由于信号中含有正常与故障两种状态的数据，且在故障数据中还可细分为轻微故障与严重故障两类.因此，特征矢量具有明显的两级尺度.表1为故障数据的多级聚类结果.由表1可见，MPC－ACM算法不但能判断出信号中是否存在故障成分，而且通过降低尺度因子的值，能对故障成分进行细分.这种方法的优点是不需提前设定聚类个数，故障成分可自动得到.虽然尺度因子的值需要人为设定，但可根据经验进行设定.这种方法在计算效率上也比常规的采用有效性指标的无监督聚类方法更高，更符合实际应用.

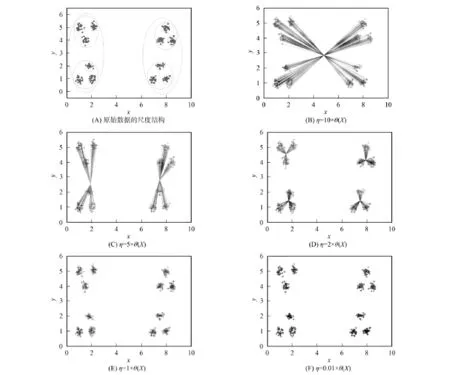
图2 不同参数下多级聚类结果Fig.2 Multi－level clustering results of different parameters

表1 故障数据的多级聚类结果Table 1 Multi－level clustering results on fault data

综上所述，本文算法通过在可能性聚类算法中引入自动融合机制进行模式搜索，增强了算法对聚类参数设置的鲁棒性.同时，多尺度因子的引入使其具有发现数据中不同尺度聚类结构的能力.本文算法的优点是参数少、易于控制，并能对数据进行多尺度分析，但该方法仍存在一些问题.首先，算法不能在指定的聚类个数下运行.该问题类似于层次聚类方法，在某些必须指定聚类个数的场合不适用.其次，关于尺度因子参数值的设置，已经发现其与数据间的距离有关，因此本文采用在数据的互距离矩阵间寻找，但理论依据仍有待论证.由实验结果可见，在没有先验知识的情况下，η＝θ（X）可得到较好的聚类结果，但其选择仍缺乏合理的理论解释.对于算法的时间与空间复杂度问题，可通过在不损失任何精度的前提下进行采样，从而降低算法的时间与空间复杂度.

［1］Duda R O，Hart P E.Pattern Classification and Scene Analysis［M］.New York：Wiley，1973.

［2］Jain A K，Duin R P W，Mao J.Statistical Pattern Recognition：A Review ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22（1）：4－37.

［3］Bezdek J C.Pattern Recognition with Fuzzy Objective Function Algorithms ［M］.New York：Plenum Press，1981.

［4］Krishnapuram R，Keller J M.A Possibilistic Approach to Clustering［J］.IEEE Transactions on Fuzzy Systems，1993，1（2）：98－110.

［5］Krishnapuram R，Keller J M.The Possibilistic c－Means Algorithm：Insights and Recommendations［J］.IEEE Transactions on Fuzzy Systems，1996，4（3）：385－393.

［6］Yang M S，Lai C Y.A Robust Automatic Merging Possibilistic Clustering Method［J］.IEEE Transactions on Fuzzy Systems，2011，19（1）：26－41.

［7］Kushnir D，Galun M，Brandt A.Fast Multiscale Clustering and Manifold Identification［J］.Pattern Recognition，2006，39（10）：1876－1891.

［8］Dave R N，Krishnapuram R.Robust Clustering Methods：A Unified View ［J］.IEEE Transactions on Fuzzy Systems，1997，5（2）：270－293.

［9］HU Ya－ting，ZUO Chun－cheng，QU Fu－heng，et al.Multi－scale Possibilistic Clustering Algorithm ［J］.Journal of Changchun University of Science and Technology：Natural Science Edition，2010，33（4）：124－127.（胡雅婷，左春柽，曲福恒，等.多尺度可能性聚类算法 ［J］.长春理工大学学报：自然科学版，2010，33（4）：124－127.）

［10］Pal N R，Pal K，Keller J M，et al.A Possibilistic Fuzzy c－Means Clustering Algorithm ［J］.IEEE Transactions on Fuzzy Systems，2005，13（4）：517－530.

［11］Yang M S，Wu K L.Unsupervised Possibilistic Clustering［J］.Pattern Recognition，2006，39（1）：5－21.

［12］Loparo K A.Bearings Vibration Data Set ［EB／OL］.2010－05－11.http：／／www.eecs.case.edu／laboratory／bearing／download.htm.

［13］CHENG Jun－sheng，YU De－jie，YANG Yu.A Fault Diagnosis Approach for Roller Bearings Based on EMD Method and AR Model［J］.Mechanical Systems and Signal Processing，2006，20（2）：350－362.