近场散射问题数值计算的超弱变分方法

栾 天，刘明辉

（1.北华大学 数学与统计学院，吉林 吉林132033；2.吉林大学 数学研究所，长春130012）

随着近场光学理论的发展，近场散射问题受到人们广泛关注.由于在远场光学中存在分辨率衍射极限，而要突破这个极限获取超分辨率的成像信息与探测信息，只能通过近场区域中的倏逝场实现.因此，研究近场散射问题获取倏逝波的信息十分重要.近场理论广泛应用于纳米技术、近场光学显微镜的研发和生物微样本的无损成像等领域［1］.目前，关于近场时谐散射问题的数值研究结果报道较少，数值模拟多采用经典的有限元方法、有限差分方法［2］和边界积分方法［3］等.但随着波数的增加，这些方法已不再适用.由于时谐波问题的解是振荡的，因此当波数较高时，需要在单位波长距离内选取足够多的点才能得到相对稳定的解.而且相位误差的积累还会导致数值污染［4］.于是要达到给定的精度，就会迫使在每个波长内使用更多的网格节点，计算量较大.基于此，本文采用另一类方法——Trefftz方法，即在区域剖分前提下，先在小单元上使用偏微分方程的解构造离散空间，并在单元交界处借助数值方法使得离散解近似地满足连续性；再将局部解“拼”接构成一个整体近似解.这类方法主要包括单位分解法［5］、间断强化法［6］、最小二乘法［7－8］和超弱变分方法［9］等.其中最典型的为超弱变分法.该方法源于区域分解技术，利用Green公式将问题转化到网格边界上处理.该方法目前已被应用于有界障碍物的散射问题中［10］.

本文针对近场光学中全内反射显微镜的散射模型，提出了相应的超弱变分方法.首先，通过对区域网格剖分引入耦合参数，利用Green公式得到了与原边值问题等价的超弱变分问题；其次，选取齐次Helmholtz方程的局部解（平面波，倏逝波）构造基底，生成试探函数空间进行离散求解；最后，通过数值实验验证算法的有效性.结果表明，该算法能有效地数值模拟近场散射问题，适用于大波数情形，所需计算量少，收敛速度快.

1 数学模型

当没有样本时，记空间中的场分布为uref，称其为参考场［11］.当在分界面Γ0上放置折射率为nS的样本S时，参考场uref与样本相互影响产生散射场us，如图1所示.记此时空间中的总场u为

图1 几何模型Fig.1 Geometry of the model

根据Maxwell电磁理论，在TM极化情形下，u满足如下方程：

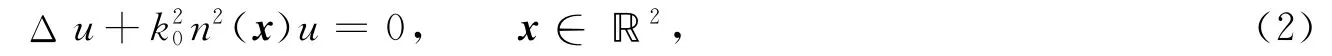
空间中的波数为k0n（x），其中折射率

实际数值模拟中，需要将无界区域截断，为此需引入人工Lipschitz边界Γ，其外法方向记为ν，将问题限制在有界区域Ω内，即Γ＝∂Ω.为了保证所选取的解符合物理要求，要求散射场us在Γ上满足吸收边界条件：

于是，由式（1）可知总场u在Γ上满足

从而所考虑的近场散射问题在数学上可描述为：已知参考场uref，求全场u满足

其中g＝（∂ν－i k0n（x））uref.

2 超弱变分问题

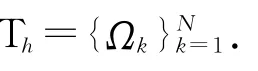
由于区域Ω中包含3种介质，因此为了使全场u在不同介质间的交界面处满足连续性条件，需引入定义在剖分网格边界上耦合参数：

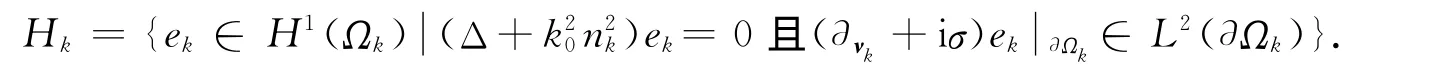
由H的定义及u满足边值问题，有

将式（6）中两式相减，得

将式（7）代入式（4），得

由u及其法向导数在Γk，j处的连续性及在Γ上满足边界条件，有

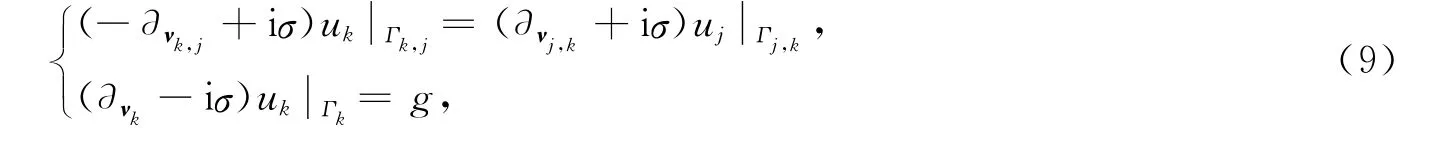
从而

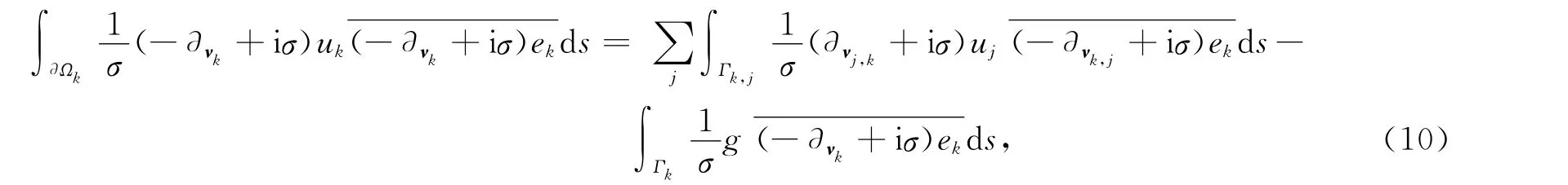
将式（10）代入式（8）并关于k求和，得

引入算子F＝（Fk）∈L（X）定义为

其中ek是边值问题

的解.

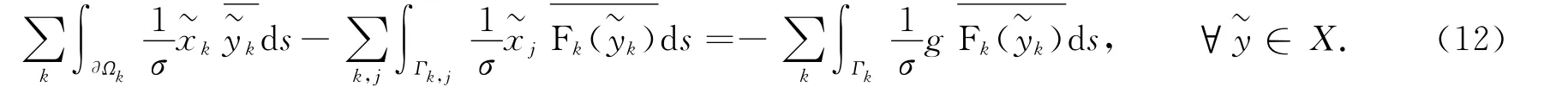
方程（12）称为边值问题（3）的超弱变分公式.

进一步，定义

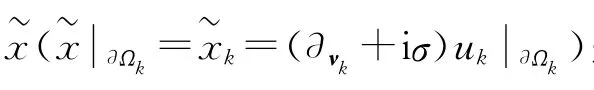
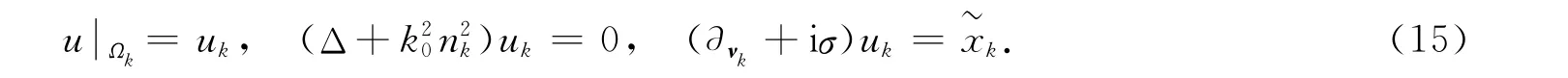
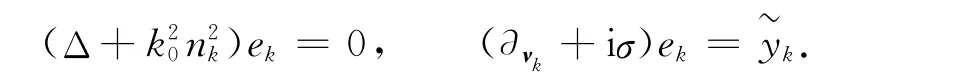
按上述相同过程可推得式（11），与式（12）相减得

从而可推得式（9）成立，即u与其法向导数在内边界连续且满足外边界条件，于是由定义知，u是边值问题（3）的解.

综上，可得：

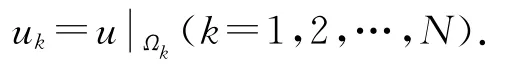
3 离散问题

选取有限维离散空间Xh⊂X代替超弱变分问题（14）中的空间X得到离散问题：求∈Xh，满足

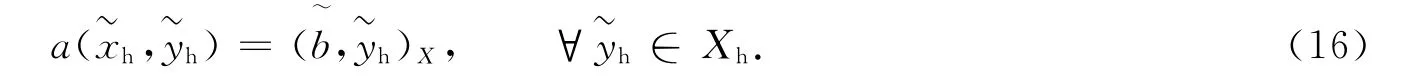
定义离散空间为

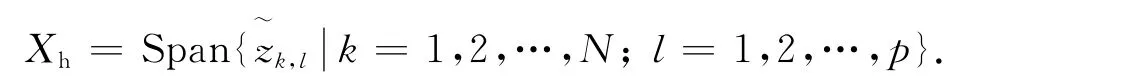
实际数值模拟中，需在每个小单元上选取方向互异的p个平面波函数和2个倏逝波函数作为ek，l.即若xk＝（xk，yk）表示单元Ωk的点，则

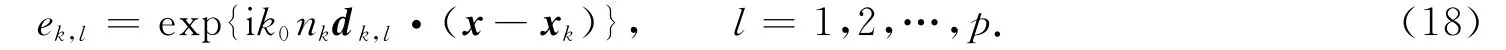
为简单，平面波的方向dk，l通常选取如下：

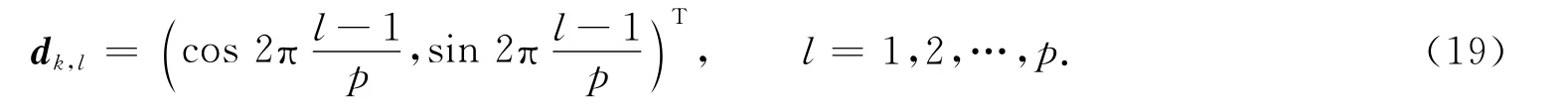
由于在全反射过程中将出现倏逝波迅速衰减，因此为了能够通过数值方法捕捉其信息，同时也选用如下倏逝波函数扩充平面波函数构造基底：

选用上述两个倏逝波，是基于本文的模型问题，依据参考场［11］uref选取的.实际应用中，可由具体模型考虑，选择适合的倏逝波.此外，由于倏逝波是向上指数衰减的，因此在实际应用中并不要求在每个单元上都应用倏逝波函数构造基底，而是仅在基座界面上方部分单元内使用即可.

4 数值模拟

程序代码使用 MATLAB语言.计算区域为Ω＝［－l，l］×［－l，l］，将Ω等矩形剖分成2nΩ×2nΩ（nΩ∈ℕ）个小单元，单元边长为l／nΩ.

例1 设k0＝1，l＝0.5，n＋＝45，n－＝75，nS＝60，θ＝π／4，则上半空间、下半空间和样本介质对应的波数分别为k＋＝45，k－＝75，kS＝60.

首先，数值求解参考场urefh.取定nΩ＝6，在每个单元上取p＝35个平面波函数.由于倏逝波向上指数衰减，因此只在界面上方第一层单元内引入倏逝波函数扩充平面波函数构造基底.数值计算得到的参考场urefh实部等高线如图2所示.

其次，为了验证算法的有效性，考察算法关于p的收敛性.由于此时存在真解［11］：

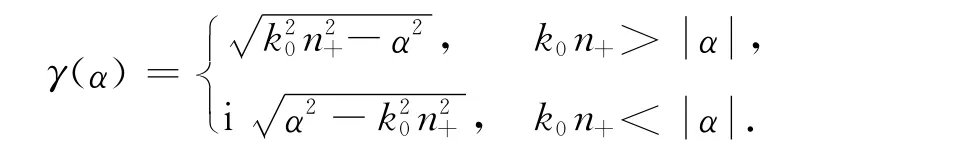
从而可以计算真解uref和数值解在Ω上的相对误差：选取初值p＝10，取nΩ＝3.当增加平面波数目，倏逝波数目保持不变，即增大p时.数值结果如图3和图4所示.图3是相对误差RE关于p的图像，图4是－lg（RE）关于p的图像.由图3和图4可见，随着基底数目的增加，误差快速衰减，表明算法是关于p收敛的，而且收敛速度较快.当p＝50时，相对误差已经不超过1%.

最后，数值计算全场uh.取定nΩ＝6，p＝50.样本大小为界面上方居中的两个单元格.间接计算散射场＝uh－，其实部等高线如图5所示.

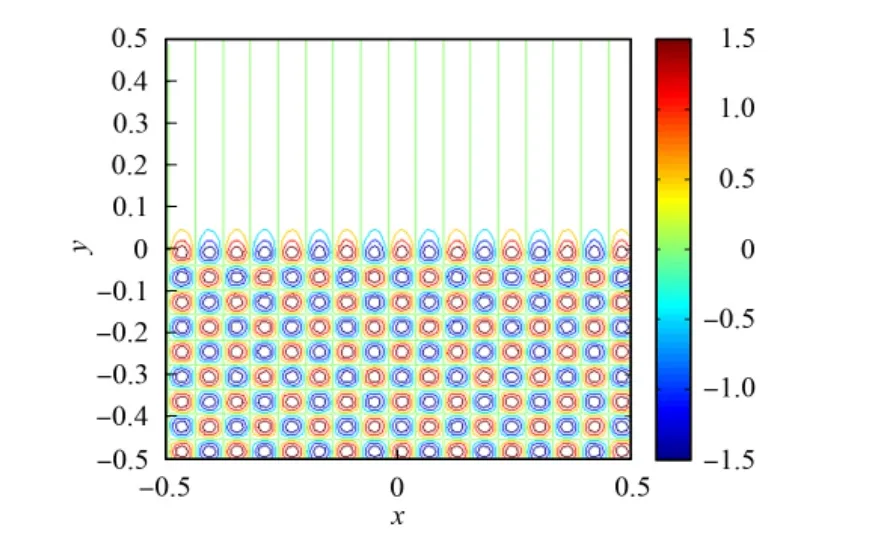
图2 urefh的实部等高线Fig.2 Contour for real part of urefh

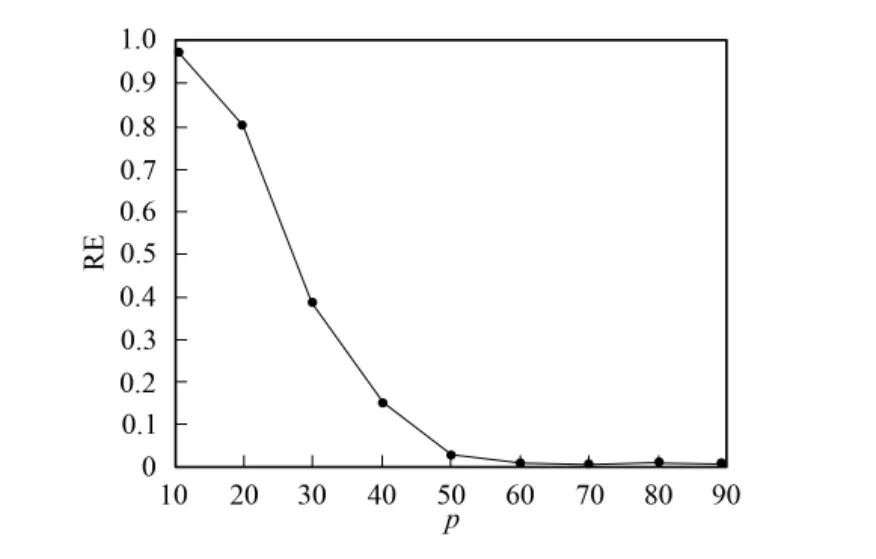
图3 相对误差关于p的曲线Fig.3 Plot of relative error againstp

图4 －lg（RE）关于p的曲线Fig.4 Plot of－lg（RE）againstp

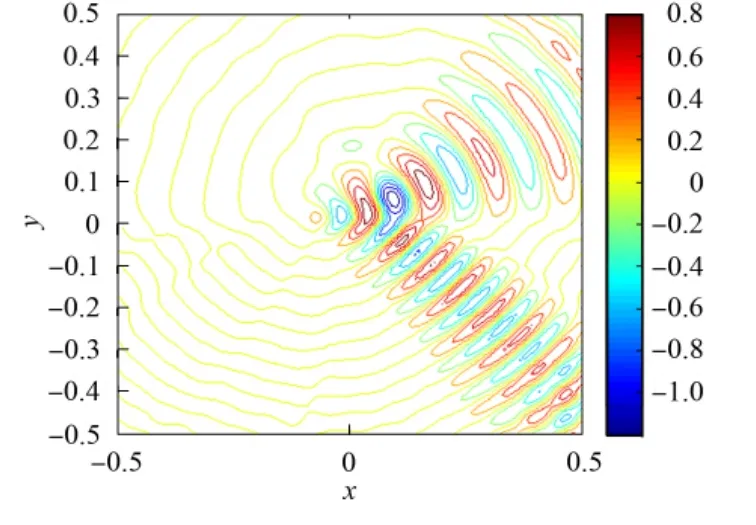
图5 ush的实部等高线Fig.5 Contour for real part of ush

综上可见，本文算法在实际数值模拟中所需剖分单元少，收敛速度快，程序运行仅需数十秒，因此能有效计算近场散射问题.

［1］Carney P，Schotland J.Inside Out：Inverse Problems and Applications［M］.London：Cambridge University Press，2003.

［2］Farakawa H，Kawata S.Analysis of Image Formation in a Near－Field Scanning Optical Microscope：Effects of Multiple Scattering［J］.Opt Commun，1996，132（1／2）：170－178.

［3］Tanaka K，Tanaka M，Omoya T.Boundary Integral Equations for a Two－Dimensional Simulator of a Photon Scanning Tunneling Microscope［J］.J Opt Soc Amer A，1998，15（7）：1918－1931.

［4］Deraemaeker A，Babuška I，Bouillard P.Dispersion and Pollution of the FEM Solution for the Helmholtz Equation in One，Two and Three Dimensions［J］.J Numer Meth Eng，1999，46（4）：471－499.

［5］Babuška I，Melenk J M.The Partition of Unity Method［J］.Internat J Numer Meth Eng，1997，40（4）：727－758.

［6］Farhat C，Harari I，Franca L P.The Discontinuous Enrichment Method［J］.Comput Meth Appl Mech Eng，2001，190（48）：6455－6479.

［7］Barnett A H，Betcke T.An Exponentially Convergent Nonpolynomial Finite Element Method for Time－Harmonic Scattering from Plygons［J］.SIAM J Sci Comput，2010，32（3）：1417－1441.

［8］LUAN Tian，WANG Yu－jie，ZHENG En－xi.Least Squares Method for Near－Field Scattering Problem ［J］.Journal of Jilin University：Science Edition，2013，51（5）：811－814.（栾天，王玉洁，郑恩希.求解近场散射问题的最小二乘方法 ［J］.吉林大学学报：理学版，2013，51（5）：811－814.）

［9］Cessenat O，Després B.Application of an Ultra Weak Variational Formulation of Elleptic PDEs to Two－Dimensional Helmholtz Problem ［J］.SIAM J Numer Anal，1998，35（1）：255－299.

［10］Cessenat O，Després B.Using Plane Waves as Base Functions for Solving Time Harmonic Equations with the Ultra Weak Variational Formulation［J］.J Comput Acoust，2003，11（2）：227－238.

［11］Li P J.Numerical Simulations of Global Approach for Photon Scanning Tunneling Microscopy：Coupling of Finite－Element and Boundary Integral Methods［J］.J Opt Soc Amer A，2008，25（8）：1929－1936.