一类超线性p（t）－Laplacian系统的无穷多周期解

张 申 贵

（西北民族大学 数学与计算机科学学院，兰州730030）

0 引 言

考虑非自治p（t）－Laplacian系统：

其中p（t）∈C（［0，T］，ℝ＋），p（t）＝p（t＋T），T＞0，且

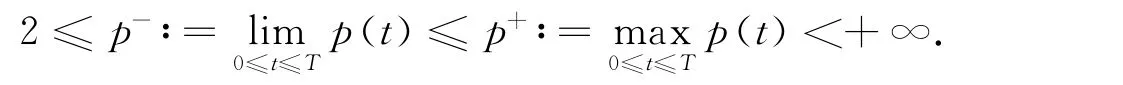
假设：

（A）F：［0，T］×ℝN→ℝ满足：F（t，x）关于变量t可测，F（t，x）关于变量x连续可微，存在a∈C（ℝ＋，ℝ＋），b∈L1（0，T；ℝ＋），使得

非自治p（t）－Laplacian系统在非线性力学模型［1］、变流体模型［2］和图像恢复模型［3］等领域应用广泛.当p（t）＝2时，Rabinowitz［4］给出了如下条件（AR）：存在μ＞2，L＞0，使得

条件（AR）可以推出非线性项▽F（t，x）是超线性的，但很多超线性函数并不满足条件（AR）.例如

本文在比条件（AR）更弱的超线性条件下，研究p（t）－Laplacian系统无穷多周期解的存在性.先将系统（1）的周期解转化为定义在一个适当空间上泛函的临界点，然后利用临界点理论中对称山路定理得到该问题无穷多解存在性的充分条件.

1 预备知识

记p（t）∈C（［0，T］，ℝ＋），定义

其范数为

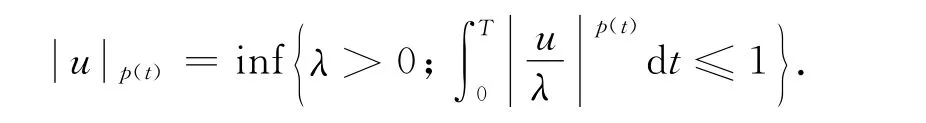
记Sobolev空间

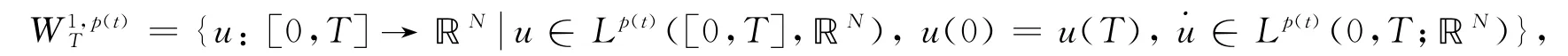
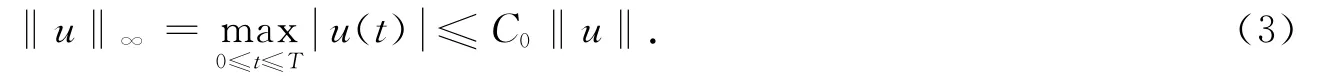
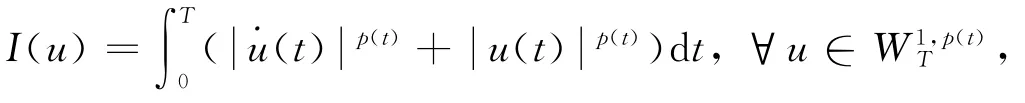
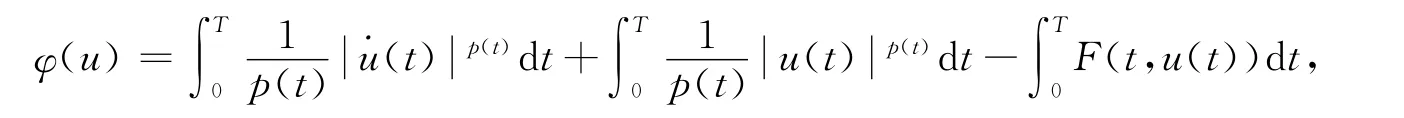
φ弱下半连续且连续可微，

定义1 设X为Banach空间，若泛函φ∈C1（X，ℝ）满足：对任何点列及任何｛un｝⊂X，由｛φ（un）｝有界，（1＋‖un‖）‖φ′（un）‖→0（n→∞），蕴含｛un｝有收敛子列，则称泛函φ满足（C）条件.

命题1（对称山路定理）［12］设E 为实Banach空间，φ∈C1（X，ℝ）是偶函数且满足（C）条件，φ（0）＝0.令E＝V⊕X，dimV＜＋∞.若φ满足：

2 主要结果

假设以下条件成立：

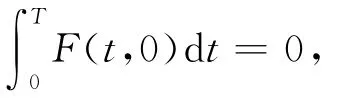
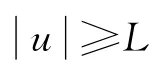
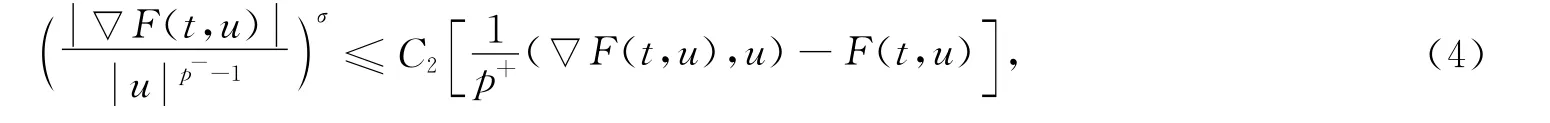
（H5）F（t，u）关于u是偶的，即F（t，u）＝F（t，－u）.

本文的主要结果如下：

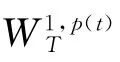
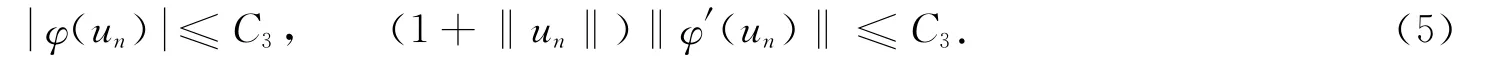
由条件（H3）和假设（A）知，存在常数C4＞0，使得

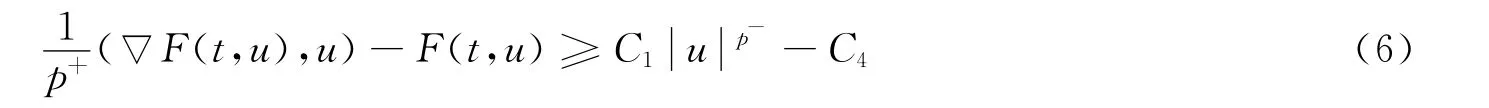
对所有的u∈ℝN和a.e.t∈［0，T］都成立.由式（5），（6），有

从而可得

由式（8）及内插不等式，有

又由式（5），当n充分大时，有

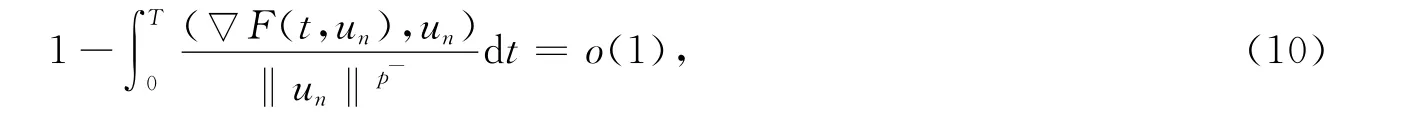
由条件（H4）和式（5），当n充分大时，有

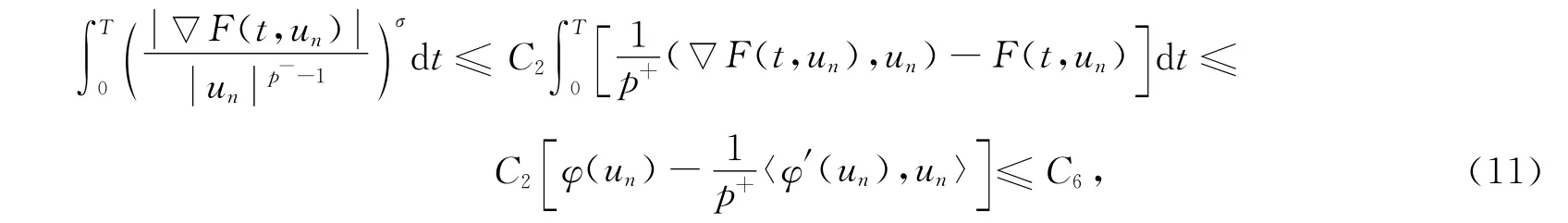
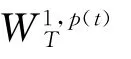
由条件（H2），存在两个正常数ε和δ，使得0＜ε＜C0，0＜δ＜ε，其中C0为式（3）中的正常数，且

由于dim W＜＋∞，有限维空间上各种范数等价，故存在正常数C7，使得对∀u∈W，有

由条件（H1）及假设（A）知，存在常数C8＞0，使得

对所有的u∈ℝN和a.e.t∈［0，T］都成立.

由式（13），（14），取‖u‖＝R＞1，又由式（4），有

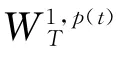
取σ＜2，则F满足定理1中条件（H1）～（H5），但不满足文献［5－11］中定理的条件.

［1］Zhikov V.On Some Variational Problems［J］.Russian J Math Phys，1997，11（5）：105－116.

［2］Ruzicka M.Electrorheologial Fluids：Modeling and Mathematial Throry［M］.Berlin：Springer，2000.

［3］CHEN Yun－mei，Levine S，Rao M.Variable Exponent，Linear Growth Functionals in Image Restoration［J］.SIAM J Appl Math，2006，66（4）：1383－1406.

［4］Rabinowitz P H.Periodic Solutions of Hamiltonian Systems［J］.Comm Pure Appl Math，1978，31（2）：157－184.

［5］ZHANG Liang，TANG Xian－hua，CHEN Jing.Infinitely Many Periodic Solutions for Some Second－Order Differential Systems with p（t）－Laplacian［J］.Boundary Value Problems，2011，33（2）：1－15.

［6］FAN Xian－ling，FAN Xing.A Knobloch－Type Result for p（t）－Laplacian Systems［J］.J Math Anal Appl，2003，282（2）：453－464.

［7］WANG Xian－jun，YUAN Rong.Existence of Periodic Solutions for p（t）－Laplacian Systems［J］.Nonlinear Anal：Theory Methods ＆ Applications，2009，70（2）：866－880.

［8］GE Bin，XUE Xiao－ping，ZHOU Qing－mei.Existence of Periodic Solutions for a Differential Inclusion Systems Involving the p（t）－Laplacian［J］.Acta Mathematica Scientia，2011，31（5）：1786－1802.

［9］ZHANG Liang，TANG Xian－hua.Subharmonic Solutions for Some Non－autonomous Hamiltonian Systems with p（t）－Laplacian［J］.Bull Belg Math Soc，2011，18（3）：385－400.

［10］ZHANG Liang，CHEN Yi.Existence of Periodic Solutions of p（t）－Laplacian Systems［J］.Bull Malays Math Sci Soc，2012，35（1）：25－38.

［11］ZHANG Liang，ZHANG Peng.Periodic Solutions of Second－Order Differential Inclusions Systems with p（t）－Laplacian［J］.Abstract and Applied Analysis，2012，38（2）：475965.

［12］Mawhin J，Willem M.Critical Point Theory and Hamiltonian Systems［M］.New York：Springer，1989.