管道补口粘接质量超声检测信号处理

周海鹏，韩赞东，王维斌，康叶伟

（1.清华大学 机械工程系，北京 100084；2.中国石油管道科技研究中心，廊坊 065000）

在管道防腐作业中，管道补口的防腐层一般采用底漆－热熔胶－聚乙烯三层结构，其中聚乙烯层通常与热熔胶复合在一起，称为热收缩带；底漆一般由热收缩带厂家配套提供［1］。相对于机械涂敷的主体管道防腐层，目前管道补口的热收缩带防腐作业均是在现场手工操作完成的，产品性能及质量受现场作业条件、操作人员操作技能影响较大，因此防腐层补口已成为管道建设质量控制中较薄弱的环节［2］。

剥离强度是衡量补口粘接质量的关键指标。一般的合格标准是：管体温度为25±5℃时，剥离强度应不小于50N／cm。目前普遍使用破坏性的剥离强度检测方法，将防腐层划开后使用测力计匀速拉起，以测力计读数作为剥离强度。这种方法操作复杂，且无法全面评估补口质量。超声检测具有无损伤、效率高、操作方便等特点，如果应用在热收缩带的剥离强度检验中，将大大提高管道补口粘接质量的检测效率，进而提高管道补口现场作业的生产效率和产品质量。

国内外针对类似粘接结构（钢和多层橡胶粘接）的超声检测研究比较广泛：高志奇［3］使用小波变换提取信号的高频和低频特征，并结合模糊模式识别算法实现了钢和橡胶粘接质量的有效评价；San Emeterio J L等人［4］分析了钢和两层橡胶形成的两个粘接界面上脱粘缺陷的时域及频域特征；张建生、李明轩先后运用人工神经网络［5］、小波变换［6］、同态解卷积［7］等信号处理方法对钢层与三层橡胶层构成的粘接结构进行研究，在不同程度上实现了粘接缺陷的特征识别与检测。

以上方法虽然在不同程度上实现了钢与橡胶粘接质量的超声检测，但对于管道补口粘接质量的评价针对性不强。笔者分析了管道补口的水浸式超声检测信号，并在理论分析的基础上选取合适的参数对检测信号进行计算，得到了可以用于管道补口粘接质量评价的超声检测方法及信号处理方法。

1 超声检测理论模型分析

使用水浸式脉冲回波法对管道补口进行检测的理论模型如图1所示。其中，检测所使用的管道补口试样由防腐层、胶层及管道层三层材料组成。水浸探头发出的信号Tw0在水中传播一定距离后到达试样表面，产生表面回波Rw0和透射波Tw1；Tw1在到达防腐层和胶层的粘接面1（胶层上界面）以及胶层和管道层的粘接面2（胶层下界面）时，会形成回波信号Rw1和Rw2。此外，信号在管道层中还会发生多次反射，形成强度较弱的多次底面回波信号Rw31，Rw32等，此处不对这部分信号进行分析。

图1 水浸式脉冲回波法检测理论模型

将超声波在表面及粘接面1，2处的反射系数分别记为γ0，γ1和γ2，水、防腐层、胶层和管道层的声阻抗分别记为Z0，Z1，Z2和Z3。根据超声波的反射公式［8］，可以得到胶层上下界面回波Rw1，Rw2的声压与入射信号Tw0的声压有如下关系：

式中：Px为超声波的声压，下标x指代对应的透射波或反射波；α1和α2为比例系数，与信号的衰减程度有关。

粘接质量的变化会导致胶层声阻抗Z2发生变化，从而引起粘接面回波信号Rw1和Rw2的强度也随之改变，对这两个信号进行分析即可得到反映粘接质量的信息。

2 检测信号分析

使用扫查系统控制水浸探头，对浸入水槽的管道补口试样的中心区域进行扫查检测，扫查范围为20mm×400mm，如图2所示。

图2 管道补口试样及检测范围

其中，试样为粘接质量依次下降的Ⅰ～Ⅲ号三组试样，Ⅲ号试样标示有明显的脱粘点。试验采用中心频率为5MHz的水浸探头，其能量较为集中，对试样的弧形表面较为敏感，得到的检测信号中间部分信号较强，两侧及焊缝附近信号较弱。这里挑选每组试样中5个典型实验点进行信号分析。

三组试样的典型检测信号如图3所示，其中（a）～（c）组信号较为清晰，可以明确分辨出表面回波Rw0、粘接面回波Rw1和Rw2等典型回波；（d）组为不理想信号，单从波形上不易区分出各典型回波。另外，根据Ⅲ号试样的回波位置特点可以判断，胶层上界面发生脱粘，此时超声波在防腐层和空气层的交接界面处发生反射，由于空气的声阻抗约为零，故脱粘界面反射系数约为－1，信号几乎完全被反射。将此时的脱粘信号记为RwA，如图3所示。对于RwA，由式（3）可知此时Z′2≈0，故γ′1≈－1；此时式（1）将变为：

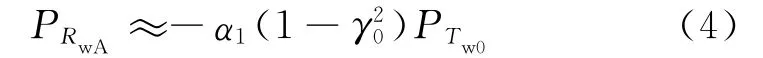
粘接面回波信号Rw1及Rw2与粘接质量有关，计算各实验点信号中Rw1与Rw2（RwA）的最大幅值，如表1所示；表1中还给出了Ⅰ号和Ⅱ号试样中Rw1和Rw2的时间差ΔT12，这一时间差使用互相关最大的方法算出。可以看出，随着管道补口粘接质量的下降，超声检测信号有以下几个变化趋势：① 粘接面1回波Rw1信号减弱，粘接面2回波Rw2信号增强。②Rw1与Rw2时间差减小（以Rw2前移为主）。③ 脱粘信号只包含一个回波RwA，与Rw1，Rw2相比信号强度显著增加。

表1 回波最大幅值对比

3 信号处理及参数计算

对于较为理想的信号，可以直接利用Rw1和Rw2（或RwA）的上述变化规律，通过观察检测波形的特征即可基本确定粘接质量的相对好坏。但对于实际检测中可能出现的不理想信号（如图3（d）所示），无法明显区分出Rw1和Rw2，也不能确定为RwA。本节将选用更加普适的计算参数，对两个波形的混合信号进行综合计算，以实现管道补口粘接质量的全面评价。

首先选择适当的时间窗口将Rw1和Rw2（或RwA）包含在内，这里取为［t0，t0＋Δt］；其中t0为表面回波的结束时刻，窗口宽度Δt＝3μs，如图3（a）～（c）中方框所示。分析图3中的信号波形可以发现，未脱粘信号中Rw2的信号强度总是大于Rw1，可以认为粘接质量下降时Rw2的增强程度比Rw1的减弱程度更为显著，因此混合信号的总强度是增强的；另外，脱粘信号RwA的强度明显大于Rw1和Rw2，此时窗口内混合信号的总强度即为RwA的强度。综合以上分析可知，粘接质量下降时混合信号总强度增加。取窗口内混合信号总强度E为计算参数，其定义式如下：

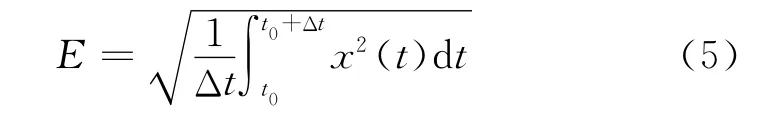
式中：x（t）为连续的波形信号。式（5）的离散化计算式为：

式中：x（k）为离散化取样之后的波形信号；nt0为时间窗口起始时刻t0对应的序号；Nt为窗口宽度Δt对应的取样点个数；由于采样频率为100MHz，故时间窗口Δt＝3μs对应的点数Nt＝300。

由式（6）定义的E值相当于时间窗口内混合信号的有效幅值，单位为mV。根据式（6）对所有检测信号进行计算，结果如图4所示。可以看出，Ⅱ号试样的计算值比I号试样更大，且Ⅲ号试样的脱粘信号特征非常明显，这与理论分析结果一致。对Ⅲ号试样的计算结果进行实物对比后可以看出，计算结果与实际情况吻合得很好。

图4 混合信号总强度E计算结果及实物对比

笔者还对检测信号进行了频谱分析。对窗口内的Rw1和Rw2混合信号进行快速傅里叶变换（FFT），其频谱如图5所示。频谱信号由Rw1和Rw2两个频率基本相同、幅度有一定差异的信号叠加而成，由文献［8］中的分析可知，叠加后的频谱与单一信号的频谱的包络线形状相同，其极大值和极小值与两个信号的时间延时Δt及幅值比有关。

频谱中的幅值强度与波形信号强度成正比，类似波形信号中的E值，频谱信号中混合信号的强度也可以作为评价粘接质量的参数。以fc＝5MHz为中心频率，选取频率窗口为［fc－0.5Δf，fc＋0.5Δf］，其中窗口宽度Δf＝8MHz。这样选取的频率窗口可以有效去除低频及直流干扰信号的影响，同时能够包含信号的绝大部分频谱，如图5所示。

取以上频率窗口内的混合信号频谱强度F为计算参数，其定义式如下：

式中：X（f）为连续的频谱信号。式（7）的离散化计

图5 混合信号频谱图

算式为：

式中：X（k）为离散化取样之后的波形信号；nfc为中心频率对应的序号，Nf为窗口宽度Δf对应的取样点个数；这里FFT的计算点数为4 096，对应采样频率100MHz，故fc＝5MHz对应的序号为nfc≈205（圆整为整数），Δf＝8MHz对应的点数为Nf≈328（圆整为偶数）。

由式（8）定义的F值相当于频率窗口内混合信号的有效幅值，与E值量级相当，单位为mV。根据式（8）对所有检测信号进行计算，结果如图6所示。可以看出，F值与E值的计算结果基本一致，Ⅲ号试样的实物对比结果也较为匹配，计算结果与实际情况吻合得很好。

图6 混合信号频谱响度F计算结果及实物对比

4 结论

（1）管道补口超声检测信号中，胶层上下界面的回波包含了与粘接质量有关的信息，其信号强度的变化趋势与粘接质量有较强的相关关系。

（2）随着粘接质量的下降，胶层上界面回波信号减弱，下界面回波信号增强，两者的时间差减小；脱粘信号中表面回波之后只有一个回波，且强度显著增大；以上特点适用于较为理想的检测波形，可实现粘接质量的直接估计。

（3）使用混合信号总强度E及频谱强度F两个计算参数，可实现对绝大部分检测信号的定量分析，理论上可实现对管道补口剥离强度的定量计算，但需要种类和数量足够多的管道补口试样来确定计算参数与剥离强度之间的定量关系。

［1］ 李爱贵，韩文礼，张其滨.三层结构热收缩带补口存在的主要问题及应对措施探讨［J］.全面腐蚀控制，2011，25（8）：37－40.

［2］ 罗锋，王国丽，窦鹏，等.管道热收缩带补口失效原因分析及相关对策研究［J］.石油规划设计，2012，23（1）：11－15.

［3］ 高志奇.复合材料粘接质量评价方法研究［J］.内蒙古工业大学学报（自然科学版），2012，31（3）：32－36.

［4］ SAN EMETERIO J L，RAMOS A，PARDO E，et al.Ultrasonic pulse propagation in a bonded three－layered structure［J］.Acoustics，2008，94（9）：4639－4644.

［5］ 张建生，李明轩.多层粘接结构中脱粘界面的人工神经网络余弦变换谱特征识别［J］.声学学报，2001，26（4）：349－354.

［6］ 张建生，李明轩.脱粘界面超声检测信号的小波多分辨率分析与重构［J］.声学学报，2001，26（3）：231－238.

［7］ 张建生，李明轩.层状粘接结构超声检测信号的同态解卷积脱粘界面定征［J］.应用声学，2001，20（1）：23－29.

［8］ 林莉，李喜孟.超声波频谱分析技术及其应用［M］.北京：机械工业出版社，2004：43－47.