微小型钢丝绳漏磁检测传感器与仪器
康宜华,黎振捷,杨 芸,邱 晨
(1.华中科技大学,武汉 430074;2.武汉华宇一目检测装备有限公司,武汉 430074)
钢丝绳在电梯、提升机、索道等设备中广泛应用,漏磁检测是目前针对钢丝绳最可靠和最有效的无损检测方法[1]。钢丝绳中的断丝、腐蚀、磨损和机械损伤等都可以通过该法检测出来。国内外已进行了大量的钢丝绳检测研究工作,并生产出各式检测设备[2]。目前,钢丝绳漏磁检测一般采用穿过式线圈磁化或者永磁磁轭式磁化,因而设计的传感器体积大且重。
笔者提出采用穿过式永久磁铁磁化的检测传感方法,最大限度地减小了传感器体积和重量。基于Ansys有限元仿真,建立钢丝绳漏磁检测磁化器模型,研究不同磁化器结构和尺寸对磁化的影响,从而优化磁化器结构尺寸,实现检测传感器的微小型设计。
1 漏磁磁化方法与装置
漏磁检测的关键在于磁化器和检测传感器的设计,目前用于钢丝绳检测的磁化方法主要有传统磁轭式永磁磁化和穿过式永磁磁化,两者各有优缺点。通过Ansys有限元分析计算,研究了两种磁化方法的磁化检测效果。建立两种磁化方法的三维仿真模型,以#28钢丝绳为例,由于其结构紧密,可以等效为钢棒[3],在其表面刻有宽2mm,深2mm,30°的槽来模拟断丝。保证穿过式磁铁和方块磁铁的厚度和磁极面积一致,磁极与钢丝绳距离一致,同时轴向覆盖长度一致。磁轭式磁化方法中方形磁铁磁极的尺寸为48mm(轴向)×32mm(周向),厚度为10mm(径向)。衔铁尺寸为146mm(轴向)×32mm(周向)×30mm(径向)。穿过式磁化方法中穿过式磁铁内外径分别为35,95mm,厚度为10mm,衔铁内外径与磁铁一致,轴向长度为126mm。图1所示为两种磁化方法的三维仿真模型。

图1 穿过式磁化与磁轭式磁化有限元模型
图2为两种磁化方法磁化效果对比图。从图2中可以看出传统磁轭式磁化法检出的漏磁信号要优于穿过式磁铁磁化法。同时计算了当钢丝绳偏离中心位置时,两种磁化形式对于钢丝绳的偏吸力,磁轭式偏吸力为45.3N,穿过式为11.5N。穿过式磁铁磁化法的优点在于方便安装,且工作过程中对钢丝绳的偏吸力较小,便于检测机构在钢丝绳上顺利运动。

图2 两种磁化方法磁化效果对比图
笔者主要对穿过式磁铁磁化方法及其检测效果进行研究,优化设计磁化器的结构尺寸,增强漏磁信号[4]。图3为穿过式磁化二维模型。从图3可看出,磁化器主体为两个穿过式磁铁和衔铁,它们与钢丝绳及中间气缝共同构成磁路[5]。通过合理选择穿过式磁铁、衔铁的内径、磁极面积以及轴向长度,以达到符合要求的磁化能力和尽可能小的体积。
2 穿过式磁铁磁化方法优化
2.1 模型介绍

图3 穿过式磁化二维模型
与第1节类似,建立穿过式磁铁磁化方法的三维仿真模型,如图1所示。模型包括磁化器、被测带缺陷钢丝绳(φ28mm,足够长)和周围空气,且模型外围的空气场足够大。永久磁铁采用NdFeB35铷铁硼永磁铁,矫顽力490 000A/m;衔铁采用通用纯铁,相对磁导率为1 000;钢丝绳模型的磁化曲线选用碳钢默认的B-H 曲线。创建物理环境模型,分别给各部分添加材料属性,手动划分区域网格(磁铁和检测区网格等级尺寸0.000 2、衔铁和钢丝绳网格等级尺寸0.002、空气部分网格等级尺寸0.004);在检测区划定检测线;计算程序,输出前述检测线上的磁场强度值,以便后续分析。在分析穿过式磁铁磁化结构的内径、外径和轴向长度时,将中间衔铁部分视为永磁铁进行分析。
2.2 穿过式磁铁内径对磁化效果的影响
保持磁铁的磁极面积(即横截面积)A=6.15×10-3m2、磁铁长度Lm=50mm 不变,R1从35~90mm每隔5mm分别取值,磁铁外径R2相应随之变化。图4显示为钢丝绳被磁化后缺陷漏磁信号轴向分量幅值Bz-PP随磁铁内径R1的变化规律。从图4可见,随着磁铁内径R1的逐渐增大,钢丝绳缺陷漏磁信号逐渐减小。这是由于磁铁能量一定,在磁铁内径不断变大的过程中,磁场分布逐渐分散化,导致钢丝绳磁化效果变差,漏磁信号逐渐降低。所以在设计过程中,在保证仪器正常运动工作的前提下,尽可能地减小磁铁内径,可达到较好的检测效果。

图4 漏磁信号Bz-PP随R1变化图
2.3 穿过式磁铁厚度对磁化效果的影响
选定磁铁内径R1为35mm,同时保持磁铁长度Lm为50mm不变,磁铁厚度由5~70mm每隔5mm取值一次。图5(a)为钢丝绳被磁化后缺陷漏磁信号轴向分量幅值Bz-PP随磁铁厚度Hm的变化规律。由图5(a)可见,随着磁铁厚度的逐渐增大,内部磁感应强度先快速增大,随后增大的斜率逐渐减小;漏磁信号强度先增大到最大值,随后保持不变,甚至有缓慢减小的趋势。这是因为磁铁厚度增加,磁势不断增强,钢索内部磁场逐渐增强,以至于慢慢达到饱和状态;同时由于背景磁场的不断增大,漏磁信号的峰峰值也很快达到最大值。磁铁厚度继续增大将不再适合本磁化器的整体结构设计,所以对于更大厚度磁铁的磁化效果未作具体研究。
从上述结果中可以得出,磁铁厚度在20~40mm间时,检测信号达到比较理想的值。表1给出了漏磁信号增大比例与磁铁重量增大比例的对比关系。M表示磁铁重量,Bδ,Mδ表示磁场强度和重量的变化比。可以看出,磁铁厚度从20mm增大到30mm的过程中,信号增大明显,同时磁铁重量增大的比例比信号增大的比例小,在可以接受的范围内;磁铁厚度从30mm增大到40mm的过程中,漏磁信号虽然继续增大,但增大比例减小,同时磁铁重量增大非常明显,不符合轻量化磁化器的设计要求。所以综合上述分析,选定磁铁厚度为30mm。

表1 磁化强度、磁铁重量与磁铁厚度对照表
2.4 穿过式磁铁磁化器轴向长度对磁化效果的影响
在确定了磁铁的最佳内、外径之后,继续研究磁化器长度对于磁化效果的影响。保持磁铁内径R1为35mm,厚度Hm为30mm不变,磁铁长度Lm从30~100mm每隔5mm依次变化。图5(b)显示为钢丝绳被磁化后缺陷漏磁信号轴向分量幅值Bz-PP随磁铁长度Lm的变化规律。由图5(b)可以看出,随着磁铁长度的增加,内部磁化强度逐渐增大,达到饱和值后保持稳定;漏磁信号先快速增大到最大值,后慢慢减小,达到稳定值。这是由于当磁铁较短(磁铁间距较小)时,磁路相对很短,钢丝绳磁化效果一般;随着磁铁长度的增加,磁路达到最佳,钢丝绳内部磁化强度达到理想值,漏磁信号也最大;当磁铁长度进一步增大时,钢丝绳磁化已饱和,漏磁信号也因为背景磁场的原因在略微减小后保持不变。
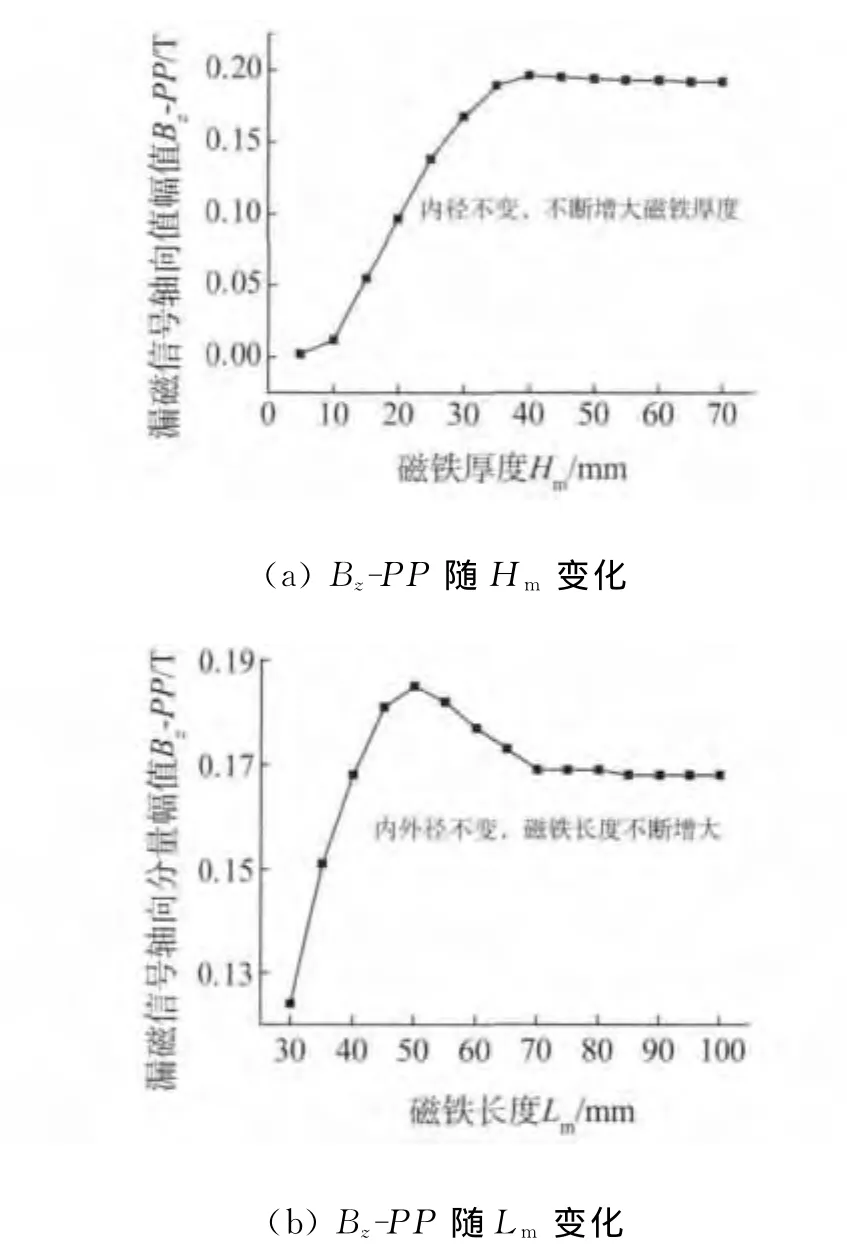
图5 漏磁信号随磁铁厚度、长度的变化图
2.5 纯铁替换磁铁的影响
在上述分析中将整个穿过式磁铁磁化器视为一整个穿过式磁铁,而实际应用中,由于铷铁硼磁铁材料价格昂贵,所以可以考虑将穿过式磁铁中间部分替换为纯铁,组合形成穿过式磁铁-衔铁-穿过式磁铁的磁化结构。保持磁化结构的轴向总长度50mm不变,逐渐增加衔铁长度,相应减小磁铁的长度。图6显示了漏磁信号Bz-PP随衔铁长度不断增大的变化趋势。从图6可以看出,随着中间衔铁的不断增加,两边磁铁长度不断减小,钢丝绳内部磁化强度和缺陷漏磁信号均会随之减小。当衔铁长度为30mm,两边磁铁长度均为10mm时,漏磁信号幅值为0.1T,相当于不使用衔铁时(0.2T)的一半,符合缺陷检出条件,所以选定衔铁长度为30mm,磁铁长度为10mm。
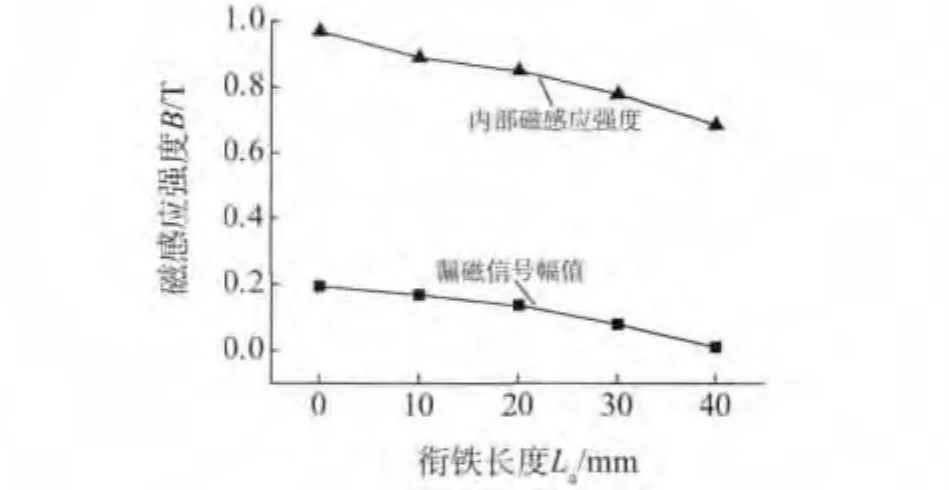
图6 衔铁尺寸对磁化的影响变化图
2.6 穿过式磁化结构优化结果
通过上述对磁化器的结构、尺寸、磁化效果的综合分析,可选择出磁化效果良好,同时体积重量很小的最优磁化器。该磁化器由两个穿过式磁铁和一个衔铁组成,两者的内外径相同,分别为35,95mm,磁铁的长度为10mm,衔铁的长度为30mm。磁化器实物如图7所示。

图7 磁化器实物图
3 信号检测方法与装置
确定了合适的磁化器以及具体尺寸后,需要选定合适的信号检测方法并设计合理的传感器检测装置。选用线圈电感作为检测传感器,在实际应用中,通常将多个线圈串联或者适当差分来真实反映缺陷信号。图8为实验室自制的线圈传感器,其主要由纯铁聚磁片和4个绕制线圈组成,线圈1,2以及线圈3,4串联后再反向连接以达到差分的目的。差分可以实现去除钢丝绳波股信号对于缺陷漏磁信号的影响的作用,在实际检测中应用意义较大。

图8 钢丝绳检测传感器示意及实物图
通过前述仿真计算得出的磁化器最佳尺寸(如2.6节所述),同时配合上述差分线圈传感器,设计出用于小直径钢丝绳检测的简单试验装置,图8所示为差分传感器在检测中的具体使用情况。图9为经过传感器、放大板、采集卡后在电脑分析软件上显示出来的断丝漏磁信号。从图10可以看出,在实验室静态环境下,上述磁化器和检测传感器配合检测出的信号信噪比良好,符合检测要求。

图9 钢丝绳微型检测传感器

图10 试验断丝信号图
4 结论
通过仿真计算和试验对比可以得出如下结论,钢丝绳断丝漏磁信号随磁铁内径R1的增大不断减小;随磁铁厚度Hm(磁极面积)的增大先快速增大,而后基本保持不变;随磁铁长度Lm的增大先快速增大到最大值,然后减小,最后达到稳定值;用纯铁代替中间部分磁铁后,漏磁信号随之减小。针对本课题设计的微型磁化器,可以选择磁铁内径为35mm,外径为95mm,长度为10mm,衔铁内外径与磁铁一致,长度为30mm。
选择合适的磁化方法,继而优化设计磁化器具体尺寸,同时对检测传感器进行合理的选择利用,既能获得较好的磁化效果和漏磁信号,又能适当地减轻单个磁化器重量,从而达到钢丝绳漏磁检测传感器的微型化设计的要求。
[1] WEISCHEDEL H R.The inspection of wire ropes in service:a critical review[J].Mater Eval,1985,43(13):1592-605.
[2] JOMDECHA C.Design of modified electromagnetic main-flux for steel wire rope inspection[J].NDT&E International,2009,42:77-83
[3] 赵敏,张东来.钢丝绳典型缺陷的漏磁场有限元仿真[J].无损检测,2009,31(3):177-180.
[4] 袁建明,武新军,康宜华.可重构斜拉索磁性无损检测机器人技术研究[J].武汉理工大学学报,2008,32(3):442-445.
[5] 林其壬,赵佑铭.磁路设计原理[M].北京:机械工业出版社,1987:95-100.

