一种基于冗余基线的时差定位去模糊方法
孙毓富,郑雪冰,柴 恒
(1.船舶重工集团公司723所,扬州225001;2.第二炮兵装备研究院,北京100085)
0 引 言
时差定位系统是当前常用的辐射源定位系统,然其对高重频固定脉冲重复周期(PRI)模式雷达常出现定位模糊甚至无法定位的现象。因此有必要研究一种有效的去模糊定位方法,改善定位系统的性能。
1 多站时差定位原理
无源时差定位是一种被动定位法,其原理主要是双曲面定位[1],通过测量同一脉冲到达各定位站的不同时刻,获得辐射源至各定位站在辐射方向的距离差,算出各主副站基线的定位双曲面(线)及交叉点,完成辐射源的快速定位。岸基定位系统对某辐射源时差定位示意图如图1所示。
要实现空间目标定位,一般采取一主三副的四站方式[2],若先选定一个笛卡尔坐标系,在脉冲序列发出的 某 一 时 刻,主站坐标 为 (x0,y0,z0),其 它3个 副 站 的 坐 标 为 (x1,y1,z1), (x2,y2,z2),(x3,y3,z3),辐射源所处坐标为原点(0,0,0),t0为信号从辐射源到主站的传播时间,各副站传播时间为ti,则各站到辐射源的距离为:

式中:c为光速。
将主副站到目标的距离相减,得双曲面方程:
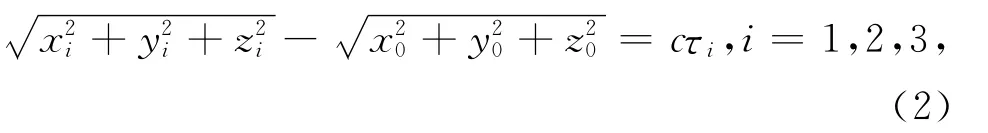
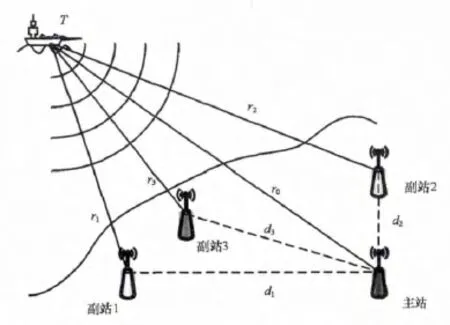
图1 岸基时差定位系统示意图
式中:τi=ti-t0,为脉冲信号分别到达主副站的时间差值。
考虑到各站位置可实时获知,主副站坐标关系为:xi=x0+Δxi,yi=y0+Δyi,zi=z0+Δzi,其 中 Δxi,Δyi,Δzi为 主 副 站 坐 标 差 值。 令r0=ct0,ri=cti,代入式(1)得:

对上式化简得:
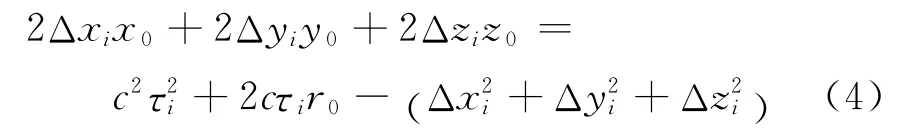

其中i=1,2,…,N为副站数。这里假设r0已知,上述方程化作矩阵形式:
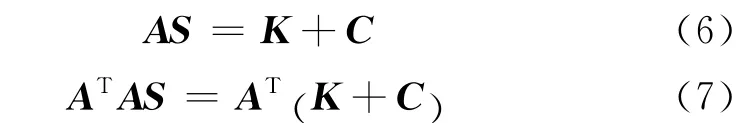
当ATA的秩等于N时,方程可表示为:
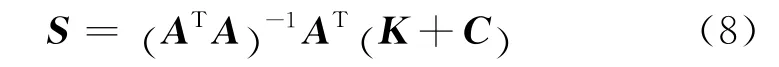
考虑A列满秩,可以唯一分解为A=UR,其中U∈Um×rr,R为r阶正线上三角阵,代入上式化简得:
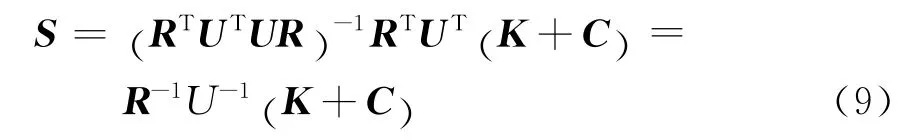
则用UR分解方法求超定方程组的最小二乘解只需求解相对简便的上三角方程组,即:
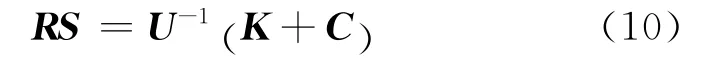
由上式线性方程,可以求得:

上述解是在假设r0已知条件下求得的,因此还需反代求参变量r0的值。将上述坐标代入下式:

在满足二次方程求解条件下,求出r0的值,再将r0值代入公式(11),可解出辐射源坐标。由于坐标解算和r0的初始值估计有关,因此初始值估计错误可能导致方程(9)无解,因此需要对r0值搜索迭代得到唯一解,若存在2个解,这就需要根据时差关系剔除镜像目标。
2 信号时差模糊及限定
2.1 高重频时差模糊分析
在上述公式推导过程中,认为到达时差是确定的,但随着多功能、多模式雷达的使用,时差定位系统常需要对高重频脉冲模式工作的辐射源进行定位,在实际应用中发现该模式下定位系统会出现较严重的定位模糊。其原因是雷达在高重频模式下相邻脉冲之间的距离间隔会远小于定位系统的各基线长度,多站间脉冲交错导致主副站之间出现时差判决的复杂多值性。
考虑脉冲序列受天线赋型的影响,需在时差检测前对脉冲序列进行预处理,包括脉冲包络检波、幅度归一化处理,还要对天线零点丢失脉冲进行补缺,以获得完整脉冲序列,保证各站精确到达时间的获取,图2为经过预处理后的各站脉冲序列的同步比较。

图2 预处理后主副站同步脉冲序列
脉冲时段的选取可参照文献[3],以主站上某一脉冲为时间基准脉冲,它与副站1、2、3各脉冲序列中先于该脉冲的最近脉冲时差分别为Δτ1、Δτ2和Δτ3,则副站相对于主站的提前到达时间差可表示为:

式中:ki为重频间隔系数,i=1,2,3,ki=…,-1,0,1,…。
则主副站在辐射方向上相应的距离差为:
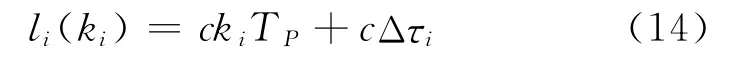
由于ki的不确定性,故无法判断每个副站相对主站的准确到达时差,这就形成了主副站时差多值性。
2.2 时间窗限定
长基线能够提高定位精度,而短基线能够减小相位、时差模糊,提高主副站之间时间同步精度。综合考虑舰载通信设备架设高度以及地球曲率的影响,为保证编队内各舰之间可靠通信,实际各舰之间距离最大不应超过35km。
式(13)中有无穷的取值,因此要实现方程快速求解,首先要根据基线长度对主副站时间差值有所限定;使得重频间隔系数k1、k2、k3在有效时差范围内搜索,考虑无论辐射方向如何,其最大距离差不应大于定位各基线长度。因此需满足:

其中di是已知的,若站型布置可以确定辐射源信号到达副站的时间先于主站时间,则将式(12)代入得:
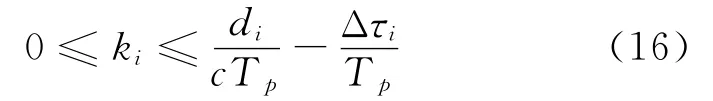

3 基于冗余基线的去模糊
上述时间窗限定后缩小了取值范围,使得搜索速度进一步加快,但仍存在多个时差值。
式(11)中当任取一组属于集合D的坐标{k1,k2,k3},k1∈D1,k2∈D2,k3∈D3,就会获得3个定位曲面,而每条基线所有可能时差系数ki的集合形成一个曲面簇,曲面簇的个数和基线个数是一致的。
尽管所求式(11)表示的坐标代入式(12)后不一定全部满足解的条件,但这些定位曲面簇在空间仍会存在若干个交点,它们都是辐射源可能存在的位置。
3.1 不同基线下定位目标分布
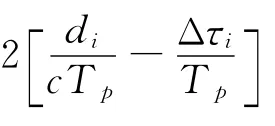
当采用另一时差定位基线时,其时差系数将会随之改变,导致定位点阵型发生相应改变。
图3(a)是B、A、D 三站定位系统;图3(b)是B、A、F三站定位系统。在图3(a)中以B、A、D三站定位时,在定位平面上解算出5个可能的辐射源位置;在图3(b)中以B、A、F三站定位时,在定位平面上解算出9个可能的辐射源位置,它们具有不同的分布特征。当然还可以在别的位置上再引入副站,得到另一种定位点分布阵型。
但无论是哪组定位基线,每个得到的定位点都远多于真实的辐射源目标数,其中许多是模糊时差得到的虚假目标坐标位置,如此众多的定位点集恶化了定位系统功能的发挥。故必须采用排除法剔除虚假目标,获得真实目标位置,或者直接确定真实坐标位置。
3.2 定位点阵的相关去模糊
从辐射源角度看无论空间存在多少个非相关的定位站,辐射源发出的同步脉冲到达各定位站的时间差是唯一的,因此所有时差系数集合Di中只有一组系数是真正的辐射源时差。反过来也就是说无论采用哪个基线组合的定位系统,真实目标必然出现在它们的共同交点上。
由于时差测量存在误差,求解的各方程在求解过程中存在迭代误差,所以难以得到精确解,因此需要设定一个容差以判断是否是同一个点,若假设类 间误差容限为δ,当满足:
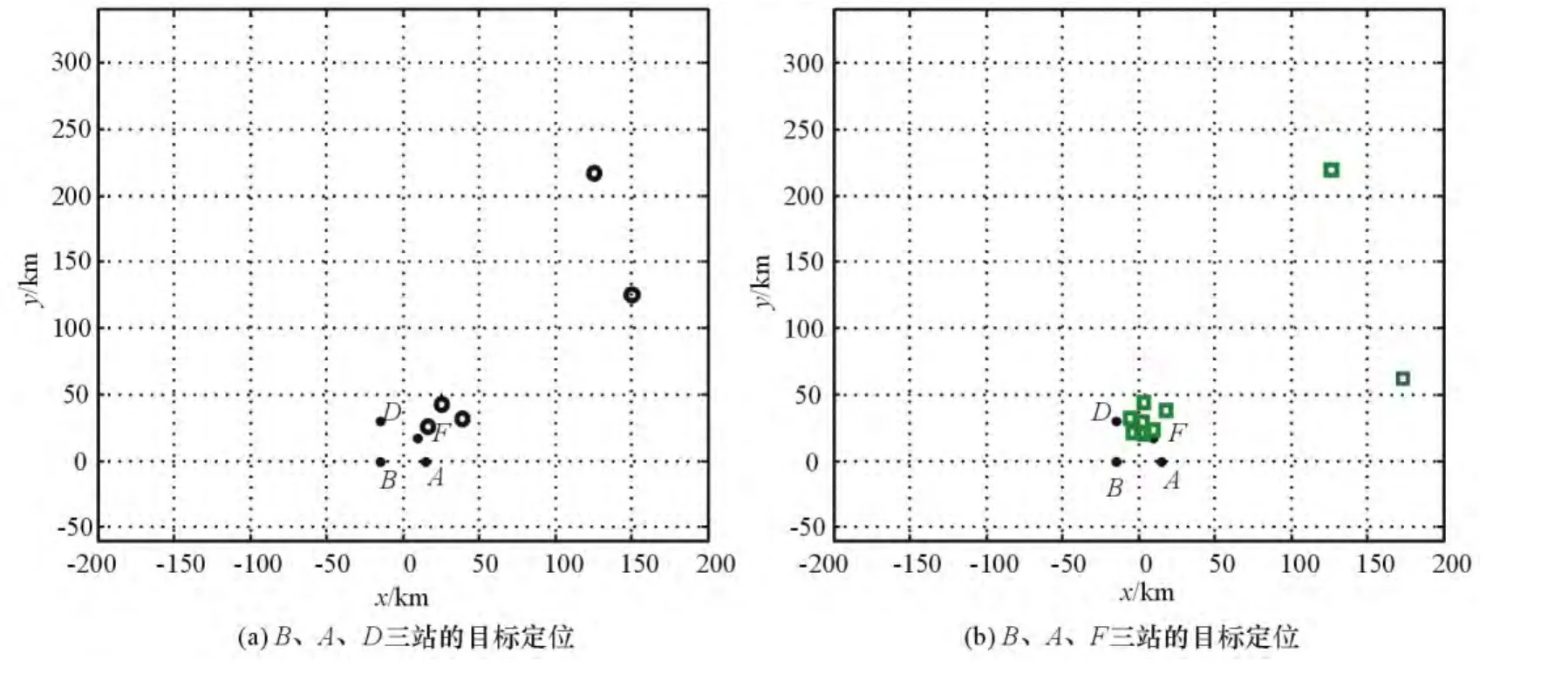
图3 各配对基线给出的定位结果

则认为P1j,P2k为同一个点,即为三条时差定位线的共同交点,因此该点就是真实目标位置所在,否则为虚假定位点。
利用上述分析及定位点判决准则,可对多组不相关基线各自的定位点集合及分布进行真假目标判决。
图4是在图3原先B、D、A三站平面时差定位系统的定位点和冗余基线的B、D、F三站定位系统定位点在同一坐标系内的显示。
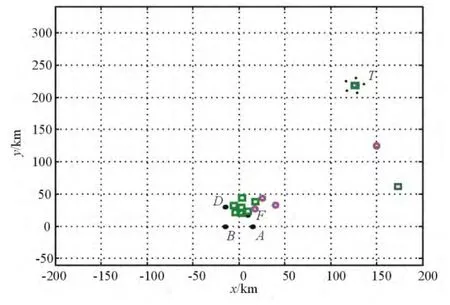
图4 基于冗余基线的定位目标去模糊
若假设δ=0.02,利用规则式(15)进行配对搜索,得出只有坐标为(125km,216km)的T点是三簇曲线的共同交点且是唯一交点,因此该坐标就是辐射源真实的位置坐标,其它均为虚假定位坐标。
4 结束语
对于高重频辐射源时差定位模糊问题,本文在分析时差定位算法的基础上,提出通过增加定位副站而获得线性无关的冗余基线,该基线可和原先基线组成新的定位系统,对基线组合的模糊解集进行配对搜索、交点判决等,可获得定位系统的公共交点,从而求得辐射源真实的位置坐标。
通过仿真证明,该方法可实现时差定位系统对高重频脉冲辐射源的定位去模糊,改善时差定位系统对目标模式的适应性。
[1]刘聪峰.无源定位与跟踪[M].西安:西安电子科技大学出版社,2011.
[2]杨林,周一宇,孙仲康.DTOA被动定位方法及精度分析[J].国防科技大学学报,1998,20(2):49-53.
[3]孙毓富,束坤,张殿友.基于多重分选的脉冲配对时差检测[J].舰船电子对抗,2013,36(6):38-41.

