基于DS证据理论的室内移动目标RSSI定位算法
苏志刚 王 铉 郝敬堂
(中国民航大学中欧航空工程师学院,天津 300300)
1 引言
随着诸如机场、车站、商场等大型室内场所日趋复杂化,出于安防、人流疏导、商业模式优化等需求,相应场所应对场所内移动人员具备主动定位的能力。提供此能力的支撑技术就是室内定位技术[1]。随着无线网络技术的发展,许多室内场所都提供了开放的WiFi 服务,利用WiFi 通信产生的到达时间(time of arrival,TOA)[2]、到达时间差(time different of arrival,TDOA)[3]、到达角(angle of arrival,AOA)[4]、接收信号强度指示(received signal strength indication,RSSI)[5]等信息可实现对室内目标的定位。基于RSSI的定位系统具有收发设备成本低、部署简单、支持设备广泛等特点,相应定位技术研究得到了广泛关注。
采用RSSI 信息进行室内目标定位的方法包括测距定位法与指纹定位法[6]。测距定位法通过RSSI 测距结合传感器位置信息进行多点定位。但在室内环境下由于电磁波受到环境中物体折射、反射、多径与遮蔽物等因素影响引起的测量缺陷使得测距精度较低,进而导致测距定位法的定位精度较差。指纹定位法将定位场景划分为诸多定位点,在离线阶段采集目标于各定位点处的RSSI 信息形成指纹数据库,将在线阶段获得的RSSI值与指纹数据库给出的先验信息进行比较,获取定位结果[7]。常见的指纹定位法包括K 最近邻[8]、朴素Bayes[9]、神经网络[10]等方法。指纹定位法定位精度更高,但所需先验信息的采集过程更加复杂。为了降低定位系统的建设复杂度,文献[11-12]通过RSSI 测距模型生成各定位点的先验信息,以取代逐点进行数据采集,此类方法与传统测距定位法相比建设复杂度相同且定位精度较高,但室内环境下RSSI测量缺陷导致的数值波动仍会对其测距精度产生影响。这一数值波动导致传感器网络在单次测量中采集到的RSSI 值可能与目标所处定位点对应的先验信息不吻合,这一问题被称为RSSI测量的不确定性[13]。
为了解决RSSI测量不确定性的问题,基于信任函数和合理推断的Dempster-Shafer(DS)证据理论被引入到RSSI 定位方法中[11-12,14]。DS 证据理论结合RSSI 测距模型通过证据构造、证据综合、决策模式等步骤获取定位结果,使得基于RSSI的定位方法的定位精度及有效性得到显著地提升。但该类方法通过RSSI构造证据的模型目前尚不完善,在一些定位场景中现有方法构造的证据可能会导致证据冲突问题[15],在证据综合阶段得到反直观结果,进而影响定位结果的精度。并且现有方法仍缺乏有效的定位决策模式,需要重复多次试验以确认决策模式所需的最佳参数,影响了定位系统建设的复杂度与定位精度。
针对当前DS 证据理论框架下RSSI定位存在证据构造不完善以及缺乏有效决策模式的问题,本文结合RSSI 信息特点,提出一种基于DS 证据理论的利用RSSI 信息对室内移动目标定位(Locating In⁃door Mobile Target with RSSI based on DS evidence theory,LIMT-DS)的方法,首先通过本文提出的证据构造方法确定传感器网络对定位环境中各位置点的证据,经过证据综合后,再通过本文提出的决策模式进行位置加权获取目标的位置估计。LIMT-DS方法使得传感器网络可以利用单次采集的RSSI 信息结合测距模型实现对室内移动目标的定位,根据仿真与实验结果,LIMT-DS 方法的定位性能优于同类方法。
2 问题描述
假设利用RSSI 进行目标定位的场景包含已知位置的K个传感器和一个未知位置的目标。传感器位于sk=[xk,yk,zk]T,k=1,2,…,K,目标的真实位置为u=[xt,yt,zt]T。第k个传感器与目标间的真实距离为
式中,‖ ⋅‖表示Euclidean 范数。该传感器接收到来自目标的信号的强度RSSI 可用对数路径阴影模型表示为[16]
式中,A为目标与传感器之间的距离为1 m 时传感器接收信息的RSSI,h为路径衰减系数,φ为阴影效应影响的衰落项。在室内环境中,墙体、家俱、人员等遮蔽物的存在使得式(2)中的φ为零均值高斯随机过程[17]。参数A与h以及φ的方差σ2取决于收发设备及系统所在的电磁环境[18],文献[19]给出了室内环境下对数路径阴影模型的相关参数的测量与拟合方法。
由式(2)可见,目标与传感器间的距离dk与传感器采集的RSSI值rk呈对数关系。rk减小的速率随dk的增大而降低。由于常用的传感器输出的RSSI测量值为整数,因此每个rk值表征的距离范围也各不相同。不妨求取rk关于dk的导数,当1 dBm 的RSSI 数值波动即可引起1 m 以上测距波动时,认为RSSI 对距离的表征能力过差。假设∂rk/∂dk=1 用于表示rk对dk的最大可容忍表征能力,故可将此时的RSSI值作为RSSI的基准
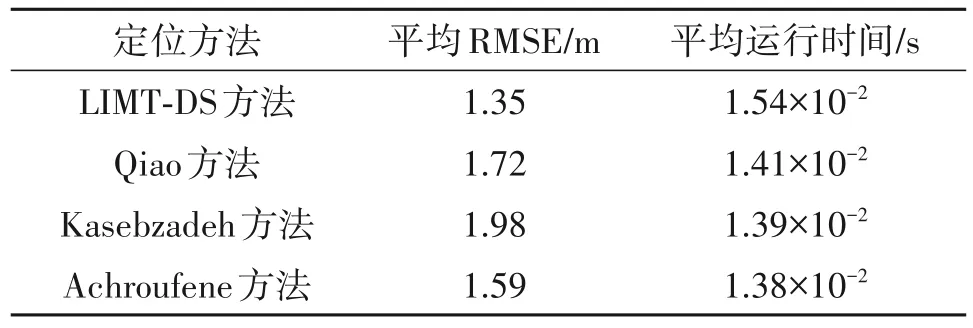
由于阴影衰落项φ的存在且传感器获取RSSI的精度较低,当rk 为采用WiFi 传感器网络获取的少量甚至单次数据实现对移动目标定位,本文基于DS 证据理论,利用定位环境中各位置点的证据实现对可能存在目标的位置点的筛选,并利用这些筛选出的位置点实现对目标的估计。 假设定位场景被均匀划分为N个位置点Cn,n=1,2,…,N,这些位置点被称为兴趣定位点。根据WiFi 传感器网络各个传感器获得的目标的RSSI 测量值,构造每个兴趣定位点的证据。 兴趣定位点的证据是指传感器sk对兴趣定位点Cn关于识别框架内的各个命题的信任程度,通常用质量函数向量mkn表示。基于RSSI 的WiFi 定位系统中,目标是否在兴趣定位点Cn上的识别框架Θ包含三个命题: 命题I:目标位于兴趣定位点Cn上。 命题Ic:目标没有位于兴趣定位点Cn上。 命题J={I,Ic}:无法判断。目标可能在兴趣定位点Cn上,也可能不在该兴趣定位点上。 质量函数向量mkn各分量间满足 基于RSSI 的WiFi 定位系统中,第k个传感器sk测量获得的目标信号强度为rk时,目标落在兴趣定位点Cn邻域的概率与条件概率密度 成正比。式(6)中,dkn表示兴趣定位点Cn与传感器sk间的距离,σ2为定位环境中阴影衰落项φ的方差。因此,可以用条件概率密度f(dkn|rk)描述传感器sk对兴趣定位点Cn关于识别框架Θ={I,Ic,J}的各个命题的信任程度,故可将质量函数向量mkn的各分量定义为 式中,ηk和wkn是用于调节向量mkn各分量间比例关系的参数。 由式(6)可知,条件概率密度f(dkn|rk)的最大值为fmax=(2πσ2)-1/2,与阴影衰落项φ的方差σ2有关。方差σ2越大,f(dkn|rk)的最大值fmax越小。在室内定位环境中,由于大量存在多径传播、透射、绕射、遮蔽等因素影响,阴影衰落项φ的方差σ2一般较大,导致条件概率密度f(dkn|rk)的数值普遍偏小,不便于用其直接描述质量函数需要引入参数ηk,用于增强条件概率密度f(dkn|rk)对质量函数的表征能力。参数ηk定义为 由式(2)可知,当rk>rlim时,目标与传感器之间的距离较小,第k个传感器sk测量的RSSI 值rk对目标与传感器间距离的表征能力较强,故应对命题I赋以更大的信任程度。rk越大则对距离表征能力越强,对命题I信任程度也越强。 通常,在基于RSSI 的WiFi 定位系统中,若质量函数向量mkn的某分量不小于另外两分量之和时,即该分量不小于0.5时,则应充分信任mkn的该分量对应的命题。当然,若mkn的某分量等于1 时,则绝对信任该分量对应的命题。然而,某个传感器绝对信任某一命题,而其他传感器无法充分信任该命题时,会产生证据冲突。为解决证据冲突问题,在兴趣定位点证据构造过程中应避免绝对信任某一命题。 为对命题I 的绝对信任而引起后续的证据冲突,需要将命题I 对应的分量仅在rk趋近于0 时方趋近于1。故而,当rk>rlim时,将参数ηk定义为 当rk≤rlim时,同样可由式(2)获知,目标与传感器之间的距离较大,过低的RSSI值rk失去了对目标与传感器间距离的有效表征,因此不再对命题I 赋以较高的信任程度,ηk取最小值并保持恒定,令ηk=此时的最大值为0.5,即仅当f(dkn|rk)取最大值fmax时,证据充分信任命题I。 关于命题J={I,Ic}的信任程度,就是目标在兴趣定位点Cn与否的信息无法明确获得的信任程度。如前所述,目标落在兴趣定位点Cn邻域的概率与条件概率密度f(dkn|rk)成正比。当f(dkn|rk)取值接近其最大值时,目标落在兴趣定位点Cn邻域内的信任度更强。反之,当f(dkn|rk)取值接近零时,目标没有落在兴趣定位点Cn邻域内的信任度更强。当f(dkn|rk)取值落在中间区域时,不好确定目标是否落在兴趣定位点Cn邻域内,因此,此时应给予命题J={I,Ic}的信任程度最强。 当f(dkn|rk)与其最大值的比值接近0.5时,认为f(dkn|rk)处于中间区域。定义为在忽略阴影衰落项的理想条件下dkn对应的RSSI数值,即 当gkn=1 时,f(dkn|rk)=0.5fmax处于中间区域,此时充分信任命题J,wkn=0.5。当gkn<1时,质量函数向量mkn中对应于命题I 的分量应占据主导,且gkn趋近于0 命题Ic对应的分量被置为零,故根据式(5)的约束,由wkn补充证据的剩余部分。当gkn>1时,对命题Ic的信任程度较高,则此时wkn随gkn的增大而减小,但为了避免绝对信任命题Ic而引发的证据冲突,将wkn设计为,从而保证wkn>0。 对于给定的兴趣定位点Cn,可利用式(7)至(9)获得传感器sk的各个命题的质量函数,并构成质量函数向量mkn,即传感器sk对兴趣定位点Cn的证据mkn。传感器网络中K个传感器可分别获得关于兴趣定位点Cn的证据m1n,m2n,…,mKn。对于兴趣定位点Cn,需要用一个证据来反映整个传感器网络对其处是否有目标的判断,故需要对K个传感器获得的关于兴趣定位点Cn的证据进行综合处理,形成整个传感器网络关于兴趣定位点Cn的唯一证据。 本文的证据综合采用Dempster 规则,该规则具备交换律、结合律等特性,且相对其他综合规则运算复杂度较低[21]。Dempster 规则就是利用兴趣定位点Cn的所有证据中的各个分量计算出综合后的证据mn的各个分量,具体表述为 式中,B与Bk是识别框架Θ={I,Ic,J}中的任意命题,其中B是综合后质量函数所表征的命题,Bk为传感器sk对兴趣定位点Cn进行信任度表征的命题, 表示参与综合的所有证据间的总冲突。在识别框架Θ={I,Ic,J}下,若使∩Bk=∅,则在K个传感器的相应命题中必含有至少一个命题I和至少一个命题Ic。因此,对于K个传感器,在识别框架Θ={I,Ic,J}下,相应的命题组合存在3K-2K+1+1种。若传感器间的证据冲突程度较小甚至不存在冲突,则所有传感器对于目标是否位于兴趣定位点Cn附近形成的证据应该是相容的,即识别框架Θ={I,Ic,J}中命题I 和命题Ic所对应的质量函数和在各个参与综合的证据中大小关系一致。这使得满足∩Bk=∅的任意命题组合中质量函数值不会同时较大,则相应的质量函数积均较小。因此,K个传感器关于兴趣定位点Cn的证据冲突程度较小时,Ln较小。当K个传感器关于兴趣定位点Cn的证据冲突程度较大时,至少存在一种命题组合,使得组合中的质量函数值均较大,从而导致Ln较大。综上所述,Ln的大小反映了K个传感器关于兴趣定位点Cn的所有证据间的总冲突。 式(15)中的∩Bk=B表示K个传感器的相应命题的共同交集为综合后的命题B。考虑命题I 在识别框架Θ={I,Ic,J}下的证据分量综合情况。显然,若使得∩Bk=I,Bk只能选择命题I 或命题J,故K个传感器的相应命题可以是至少一个命题I 与若干命题J 的组合,即有2K-1 种组合,故可得命题I 的证据分量将是所有组合积的总和。同理,对于命题Ic在识别框架Θ={I,Ic,J}下的证据分量综合时,K个传感器的相应命题也有2K-1 种组合,每组组合中至少有一个命题Ic,相应的证据分量也将是所有符合约束的组合积的总和。 命题J 的情况相对特殊,在识别框架Θ={I,Ic,J}下,若使得∩Bk=J,则每个传感器的相应命题Bk均应为命题J,故可得命题J的证据分量综合结果可简化为 对于给定的兴趣定位点Cn,对识别框架Θ 各个命题的证据分量综合后获得,由此可形成整个传感器网络关于兴趣定位点Cn的证据mn= 在基于RSSI 的WiFi 定位系统中,根据各个传感器所获得目标的单次RSSI值,可以构造并综合出传感器网络关于各个兴趣定位点的证据mn。根据各个兴趣定位点的证据及兴趣定位点的空间位置信息,对目标所处空间位置进行决策,形成对目标位置的估计,这一过程被称为目标定位的决策模式。 最大质量模式是一种较为直观的目标定位决策模式。最大质量模式利用证据mn的分量更直观地表征了传感器网络对目标位于兴趣定位点Cn的信任程度,因此,选取分量最大的兴趣定位点Cmax坐标作为定位结果[12]。最大质量模式只利用了单个点,忽略了Cmax附近具有较大的兴趣定位点的影响,导致定位性能较差。传统质心模式[14]修正了最大质量模式利用兴趣定位点过少的问题,选取分量较大的前N′个兴趣定位点,并利用相应对兴趣定位点进行位置加权,获得目标的位置估计。显然,传统质心模式的性能受到N′值大小的影响,最佳N′值的选取通常需要多次实验,且最佳N′值与系统工作环境相关。因此传统质心模式提高了定位系统的建设复杂度,且不恰当的N′值选取会对定位精度产生影响。 为了解决有效兴趣定位点的选取问题和定位系统对目标实时定位的需求,LIMT-DS 方法引入Jousselme 距离。Jousselme 距离是一种基于范数定义的证据差异度量函数,在差异度量过程中综合考虑了各确定性与不确定性命题分量对证据间差异程度的影响,在本文研究问题的识别框架Θ 下运算复杂度较低[15]。LIMT-DS方法通过该距离归一化后的特点完成目标存在可能性较高的兴趣定位点的选取,而后采用质心加权方式实现对目标定位。 两兴趣定位点C1和C2的证据m1和m2间的Jousselme距离定义为 式中,D为Jaccard 系数矩阵,在识别框架Θ={I,Ic,J}下, 根据式(5)的约束,在基于RSSI 的WiFi 定位系统中Jousselme距离可以简化为 在基于RSSI 的WiFi 定位系统中,Jousselme 距离J(m1,m2)用于表征两证据m1和m2对确定性命题的信任度间的差异程度,取值范围在0 与1 之间。当J(m1,m2)=0 时,说明定位系统对于兴趣定位点C1与C2点是否存在目标的判断一致。反之,随着J(m1,m2)的增大,定位系统对于兴趣定位点C1与C2点是否存在目标的判断的差异性增大。 类似于传统质心模式,LIMT-DS 方法也需要选择一定数量的兴趣定位点用于对目标的定位。为选择出具有较高信任度水平的兴趣定位点,需要确定一个选择的基准。由于J(m1,m2)的大小可以反映两个兴趣定位点C1与C2点是否存在目标的可能性差异,因此,可利用该距离信息评价某兴趣定位点Cn的邻域内目标存在可能性的变化剧烈程度,即定义兴趣定位点Cn的归一化Jousselme距离为 式中,P为兴趣定位点Cn的邻近定位点组成的点集,若定位场景中的兴趣定位点是均匀分布的,则点集P是由以兴趣定位点Cn为中心、边长为2 倍点间隔的正方体表面上的点所构成。Cp1与Cp2是点集P中关于Cn对称的一对点,Np为点集P中对称点对的数目,cp1和cp2分别是点Cp1与Cp2的空间位置矢量。 归一化Jousselme 距离Gn(Cn)较大时,兴趣定位点Cn邻域内目标存在可能性的变化剧烈程度增大,因此可以将使Gn(Cn)最大化的兴趣点作为基准点Cref 将基准点Cref的证据mref的分量作为兴趣定位点选择的门限,选取满足 的兴趣定位点Cv,其中v=1,2,…,V。所有的兴趣定位点Cv构成候选点集{Cv}。利用候选点集{Cv},可对目标位置进行估计 式中,cv为兴趣定位点Cv的空间位置矢量为兴趣定位点Cv的证据mv的分量,Lv为兴趣定位点Cv的证据总冲突,可由式(16)计算。由式(24)可见,是候选点的权值。如此选择权值的原因在于候选点Cv对应的较高且Lv较低时表明定位系统中更多的传感器证据认为目标存在于该兴趣定位点Cv。 基于前面的准备,可以将LIMT-DS 方法的具体实施步骤做如下描述: 步骤1针对给定RSSI 定位系统测定参数A、h与σ,并根据式(3)计算出RSSI基准值rlim; 步骤2确定系统定位区域的所有兴趣定位点Cn,根据传感器sk采集的目标信号的RSSI值rk,以及兴趣定位点Cn与传感器sk间的距离dkn,利用式(6)计算出该点的概率密度f(dkn|rk); 步骤3利用RSSI 值rk,由式(10)确定参数ηk,由式(11)~(14)确定参数wkn; 步骤4根据获得的概率密度f(dkn|rk)及参数ηk、wkn,由式(7)~(9)确定传感器sk关于定位点Cn的证据mkn的各个分量; 步骤5利用式(15)~(17),获取各传感器间的证据冲突程度Ln,并将各传感器对兴趣定位点Cn的证据综合为单一证据; 步骤6对全部兴趣定位点完成证据综合后,由式(21)计算兴趣定位点Cn的归一化Jousselme 距离Gn(Cn),选取使Gn(Cn)最大化的兴趣点以确定选择门限 步骤7根据选择门限将符合条件的兴趣定位点构成候选点集,并根据式(24)用质量函数与冲突程度作为权值对候选点集中的点进行位置加权求和,获得相应的目标位置估计。 由LIMT-DS 方法的步骤可见,该方法可通过WiFi 传感器网络单次获取对目标RSSI 数据的单次采集实现对目标定位。LIMT-DS方法通过证据构造与运算归一化Jousselme 距离等步骤提高了定位精度,而此类步骤的引入也会提高方法的时间复杂度。时间复杂度体现了定位方法的实时性,需要对LIMTDS方法的时间复杂度进行分析以评估其综合性能。 假设定位环境中存在K个传感器与N个兴趣定位点,构造一个传感器关于一个兴趣定位点的证据所需的时间为t1,综合K个传感器关于一个兴趣定位点的证据所需的时间为t2,计算一个兴趣点的证据对应的归一化Jousselme 距离所需的时间为t3。为求取时间复杂度上界,不妨假设对全部N个兴趣定位点均进行位置加权,不满足候选点集条件的兴趣定位点权值被置为0,加权过程中每个兴趣定位点所需的运算时间为t4。则LIMT-DS方法的时间复杂度上界为:O(KNt1+Nt2+Nt3+Nt4)。 LIMT-DS 与现有的基于DS 理论的RSSI 定位方法[11-12,14]均采用了类似的识别框架与Dempster 综合规则,因此在证据构造与证据综合阶段时间复杂度基本相当。而现有方法普遍采用的传统质心模式仅通过比较各兴趣定位点证据的一个分量即直接进行位置加权,因此现有方法的时间复杂度上界为O(KNt1+Nt2+Nt4)。 综上所述,本文提出的Jousselme 距离加权模式在LIMT-DS 方法中增加了一定的时间复杂度。但传统质心模式需要在系统建设过程中逐步进行测试以获取单一的最佳取值,因此LIMT-DS 方法在运算量提高的同时降低了定位系统的建设难度并提高了定位精度。 为验证LIMT-DS 方法性能,利用MATLAB R2018a 软件设置仿真平台进行验证。仿真场景为20 m × 20 m 的方形区域,以1 m × 1 m 的间隔在环境中均匀设置兴趣定位点。在一组仿真中,将8 个传感器(编号为AP1~AP8)与1个定位目标随机部署在该区域内,且假设传感器的通信半径均可完整覆盖仿真区域,图1 展示了一次随机节点部署中传感器与定位目标的分布情况。根据式(2)对应的对数路径阴影模型生成各传感器接收到的来自定位目标的RSSI,根据文献[19]在室内环境中对WiFi信号的测量结果设置式(2)中的参数A=-33.6 dBm,h=2.35,阴影衰落项φ的标准差σ=2.61 dBm。传感器对定位目标进行独立的RSSI采集,为验证单次数据采集的定位性能,每进行1 次RSSI 采集即通过相应定位算法进行1 次定位运算,持续采集RSSI 进行50 次定位运算并计算各算法对应的均方根误差(Root Mean Square Error,RMSE)。之后重新进行随机的传感器与目标部署,并再次进行50次定位运算,以此循环进行仿真。每组仿真共随机进行300次节点部署,每次部署独立进行50 次定位运算,即每组仿真中共进行300 × 50=15000 次定位运算,将各定位算法在300 次部署下的RMSE 取平均,得到平均RMSE作为性能指标。 本文用于对比的方法包括Kasebzadeh 方法[11]、Achroufene 方法[12]与Qiao 方法[14]。三种对比方法均是基于DS 理论的RSSI 定位方法,三者关于证据的构造方法不同。其中,Kasebzadeh 方法认为传感器sk采集的RSSI 数值相对其他传感器越小则应赋予命题J 越高的信任程度。Achroufene 方法认为若概率密度f(dkn|rk)较小则赋予命题J 更高的信任程度。Qiao 方法通过传感器测量距离与定位点参考距离计算定位点隶属度,隶属度较高时绝对信任命题I,隶属度处于中间区域时赋予命题J更高的信任程度。三种对比方法均采用Dempster 规则进行证据综合,且均可采用传统加权模式作为决策模式。为了避免传统加权模式中N′的数值选取不当对对比方法性能产生不利影响,本文进行多次测试将各对比方法的N′值设置为在当前仿真场景下表现出最佳性能的数值。 根据7.1节描述的仿真条件进行一组仿真,各算法定位误差分布区间的累积概率分布如图2 所示。由图2可见,在定位误差小于3 m时,Qiao方法与Kas⁃ebzadeh方法的累计概率均约为80%,Achroufene方法的累计概率为90%,LIMT-DS方法性能最优,累计概率达到了95%。各方法的性能差异与对应的证据构造模型相关。其中,Kasebzadeh 方法的构造模型仅考虑的RSSI 数值大小而未充分考虑阴影衰落对RSSI的影响。Achroufene方法的证据构造模型使得定位环境中可能同时出现多个对目标存在信任程度较高的区域。Qiao 方法的证据构造模型在一些兴趣定位点处会使得部分传感器证据绝对信任命题I,进而使式(15)运算的证据综合结果收到影响,从而影响定位精度。 在保留7.1 节其他仿真条件的前提下,分别在设置4~8 个传感器的情况下各进行1 组仿真,各方法性能随传感器数目的变化如图3 所示。由图3 可知,各方法的平均RMSE 均随传感器数目增加而下降,且在各传感器数目下LIMT-DS 方法均表现出较好的性能。 在保留7.1 节其他仿真条件的前提下,将阴影衰落标准差σ由2 dBm 逐渐增加到4 dBm,每增加0.2 dBm 标准差进行1 组仿真,各方法性能随阴影衰落标准差的变化如图4 所示。由图4 可知,各方法的平均RMSE均随阴影衰落标准差的增加呈上升趋势,LIMT-DS 方法则在各阴影衰落标准差下均表现出较好的性能。 为验证节点布局对各方法性能的影响,通过几何精度因子(Geometric Dilution Precision,GDOP)来描述节点布局对定位的影响程度。RSSI定位机制下的GDOP计算方法由文献[22]给出。在7.1节所述的仿真场景中,各定位点的GDOP一般处于[0.04,0.2]这一区间内,GDOP越低说明节点布局越适宜定位。 保留7.1 节所述的仿真条件,在预设特定的GDOP 值后,随机进行传感器部署并计算当前部署下仿真场景中各定位点的GDOP。选中任一GDOP等于预设值的定位点作为定位目标位置,在该位置进行50 次数据独立的定位。之后再次随机进行传感器部署并再次选取定位点生成数据。重复300次上述过程,求取预设GDOP 值下各定位方法的平均RMSE 作为性能指标。不同预设GDOP 值下各算法的性能如图5 所示。由图5 可知,在GDOP 较低,即节点布局有利于定位的条件下,LIMT-DS方法、Kas⁃ebzadeh 方法和Achroufene 方法表现出了相近的性能。随着GDOP的增加,节点布局逐渐不利于定位,各方法的平均RMSE 均有所上升,其中Kasebzadeh方法的平均RMSE 明显增加,这说明Kasebzadeh 方法性能受节点布局的影响十分严重。LIMT-DS方法的性能且相比其他方法始终保持最优,且平均RMSE随GDOP 上升幅度较小,说明LIMT-DS 方法在多种节点布局条件下均可获取精度较高的定位结果。 上述仿真过程均只利用单次RSSI 采集进行定位仿真并获取算法性能。为验证少量采集RSSI 对定位性能的影响,在保留7.1 节其他仿真条件的前提下,将每次定位所需的RSSI 采集次数从1 次逐渐增加到5 次,完成RSSI 采集后对采集到的数据进行均值滤波,再将滤波结果代入各定位算法。在1~5次RSSI 采集的条件下进行5 组仿真,各方法性能随RSSI采集次数的变化如图6所示。 由图6可见,随着RSSI采集次数的提高,各方法的平均RMSE均有下降,这是因为在定位目标固定的前提下均值滤波削弱了阴影衰落对定位的影响。而LIMT-DS方法在RSSI单次或少量采集的条件下均表现出最好的性能,说明LIMT-DS 方法采用单次采集数据和少量采集数据时均可起到较好的定位效果。 为验证本文提出的Jousselme 距离加权模式对LIMT-DS 方法性能的影响,在7.1 节所述条件下进行1 组仿真,每次仿真定位运算中通过LIMT-DS 方法进行证据构造与综合,并通过Jousselme距离加权模式与预设不同N′的传统质心模式进行位置决策。决策模式随N′值的性能变化如图7所示。由图7可知,传统质心模式的平均RMSE 随N′值的上升呈现先下降后上升的趋势,这是因为适当的N′值使得目标存在可能性较高的数个定位点均参与位置加权,过大的N′值则有可能导致过多定位点在加权过程中干扰定位结果,在N′=20 时传统质心模式表现出较好的性能。而Jousselme 距离加权模式的性能与N′值无关,平均RMSE 始终为1.73 m。将其以一条直线的形式绘制在图7 中,与传统质心模式进行对比,可以发现其优于传统质心模式的最佳性能,说明Jousselme 距离加权模式是一种可以实时获取最佳位置加权结果的决策模式。 在保留7.1 节其他仿真条件的前提下,将兴趣定位点划分的最小间隔从0.5 m逐渐增加到2.5 m,每增加0.5 m间隔进行1组仿真,各方法性能随兴趣定位点间隔的变化如图8所示。由图8可知,各方法的平均RMSE 均随兴趣定位点间隔的缩小而减小,这是由于兴趣定位点分布越密集则其引入加权过程的位置信息也越丰富。LIMT-DS方法的性能在兴趣定位间隔为1 m 时已经趋于稳定,而过小的间隔会使得大量兴趣定位点增加定位运算的时间复杂度,因此以1 m为间隔进行兴趣定位点划分较为合理。 为进行实验获取数据验证LIMT-DS 方法性能,搭建实验系统如图9 所示,并通过文献[19]给出的方法通过回归处理的方式拟合试验环境中对数路径阴影模型的相关参数。定位系统安置在10 m ×15 m 的室内,布置8 个传感器(编号为AP1~AP8),以1 m × 1 m 的间隔在室内设置兴趣定位点。采集定位数据过程中,目标由起点(2,5)出发,沿虚线路径到达终点(8,11)。目标向定位系统发射2.4 GHz的WiFi嗅探帧,路径上经过的每个兴趣定位点作为采样点,每个采样点处定位系统采集5组数据,路径上有25 个采样点,共采集125 组数据,并在CPU 为Intel i5-7500 3.40 GHz、内存为16 GB 的计算机平台上用MATLAB R2018a软件进行定位运算。 利用实验数据,计算每个兴趣定位点的定位误差的RMSE,并对25 个兴趣定位点处的RMSE 取平均,得出每种方法目标定位性能如表1所示。其中,平均运行时间表示各方法在一次定位运算中所花费的平均时间。由表1 可见,Qiao 与Achroufene 方法的定位精度均优于Kasebzadeh 方法,而LIMT-DS方法的定位精度最高,优于其他方法15%以上。与本文第6 节中的分析相同,由于LIMT-DS 方法提出的决策模式的复杂性,定位平均运行时间增加约10%,牺牲了部分运算速度获得精度更高的定位结果。同时,LIMT-DS 方法不需要前期逐步测试的决策模式也降低了定位系统建设的难度。 表1 各方法实验性能Tab.1 Experimental performances of different approaches 为验证仿真性能与实际性能的差异,在与实验相同的环境参数与节点部署条件下,通过式(2)生成仿真数据进行500 次独立仿真,得到各方法的仿真性能以及仿真性能与实验性能的差异如表2 所示。由表2 可知,各方法的仿真性能与实验性能均存在20%左右的差异,这一差异是由实际环境中参数测量存在一定误差所导致的。但各方法的平均RMSE 大小关系在实验与仿真中均保持一致,且无论在实验还是仿真中,LIMT-DS 方法相较对比方法均表现出最佳性能。 表2 各方法仿真性能Tab.2 Simulation performances of different approaches 本文提出的LIMT-DS 方法在定位过程中结合对数路径阴影模型与实测RSSI,通过本文提出的证据构造方法生成各传感器的证据,并进行综合,最终通过本文提出的Jousselme 距离加权模式得到定位结果,可以通过传感器网络单次获取的RSSI数据进行目标定位。 相比于现有的基于DS 理论的RSSI 定位方法,LIMT-DS 方法提出了更适用于RSSI 定位问题的证据构造方法,减少了阴影衰落与证据冲突对定位结果的影响。同时提出了可以实时确定位置加权范围的决策模式,以降低定位系统的建设难度。本文从传感器数目、阴影衰落标准差等多方面对LIMTDS 方法的性能进行了仿真分析,并与其他基于DS理论的方法进行了对比。仿真与实验结果表明,LIMT-DS方法相比同类方法在室内定位环境下具有更加良好的性能。3 兴趣定位点的证据构造
4 兴趣定位点的证据综合
5 目标定位的决策模式
6 基于DS理论的RSSI定位方法
7 仿真结果
7.1 仿真条件
7.2 不同算法性能对比
7.3 传感器数目对定位性能的影响
7.4 阴影衰落标准差对定位性能的影响
7.5 节点布局对定位性能的影响
7.6 RSSI采集次数对LIMT-DS方法的影响
7.7 决策模式对LIMT-DS方法的影响
7.8 兴趣定位点间隔对定位性能的影响
8 实验结果

9 结论

