基于射频功放非线性建模的欺骗干扰识别
甘一鸣,孙闽红,郑 琴,邱 雨
(1.杭州电子科技大学,杭州310018;2.杭州谱恒科技有限公司,杭州310018)
0 引 言
欺骗干扰是指干扰机发射与真实信号相似的虚假信号,容易被接收机捕获接收,以达到干扰的目的。与压制式干扰相比,欺骗干扰效率高,不易被察觉,威胁更大,已经成为雷达与通信系统的主要威胁[1]。
抗欺骗干扰的前提是接收机能够检测识别出欺骗干扰。目前国内外针对欺骗干扰识别方法的研究主要集中在基于特征提取的干扰识别算法[2-5]。基于特征提取的干扰识别算法是通过分析真实信号与干扰信号在时域、频域和空时域等之间的差异特性,构建特征集来识别干扰。这些方法都要求干扰信号在某个域上与真实信号不重叠,而欺骗干扰往往在时、频、空等多域与真实信号完全或者部分重叠,识别效果往往不太理想。
近年来,研究人员发现即使是同一条生产线制造出来的同一批次的射频元器件也存在着细微差异[6-9]。这些细微差异使得输出信号附加上了不影响信息传输的“指纹”特征。因而,基于发射机射频元器件非线性特性附加在发射信号中“指纹”特征的射频辐射源识别(RFID)技术[10]逐渐成为研究热点。然而,这些提取“指纹”特征的方法多是通过信号分析手段,寻找的依然是信号在时域、频域或时频域的特征参数,识别效果依然不够理想。本文从另一角度,即通过对欺骗干扰机的射频元器件模块建立统计模型,以模型参数作为区分真实信号和欺骗干扰信号的特征向量,实现检测识别欺骗干扰的目的。不失一般性,假定干扰机除射频放大器外的其它射频元器件均工作在理想状态,本文重点分析射频放大器的统计模型并研究基于该模型的欺骗干扰统计检测识别方法。
1 射频功率放大器模型特征参数提取
Volterra级数核向量可以唯一地表示一个放大器模型[10],故可作为功率放大器的特征向量。Volterra级数模型常用于弱非线性电路的建模,其简化模型包括Hammerstein模型和 Wiener模型,其中Hammerstein模型由一个非线性模块再串联一个线性动态模块而构成,结构清晰,参数较少,能够描述常见的非线性系统,所以得到了广泛的应用。
Hammerstein模型非线性部分的系统方程为:

式中:u(k)为非线性系统的输出;x(k)为非线性系统的输入。
Hammerstein模型线性部分的系统方程为:

式中:y(k)为线性系统的输出;u(k)为线性系统的输入变量;z-1为后移算子,且有:A(z-1)=1+a1z-1+a2z-2+…anaz-na,B(z-1)=b0+b1z-1+b2z-2+…bnbz-nb。
将式(1)代入式(2),得:

令hij=ribj,可得:

可令h=[h10h11…h1nb…hp0…hp1…hpnb],为要提取的特征参数向量。
Hammerstein模型的辨识可采用最小二乘法[11]、神经网络[12]、粒子群[13]等算法[14]。
2 欺骗干扰的似然比检测
根据式(4),接收机接收到的分别由真实发射机和欺骗干扰机发射的信号可建模为:

式中:h1与h2分别为真实发射机和欺骗干扰机的模型参数向量;υi设为服从均值为0、方差为σ2iI的高斯分布噪声向量;Pi为功放输入信号矩阵,若使用输入信号记忆深度为2的二阶Hammerstein模型,输入信号长度为M,则有:
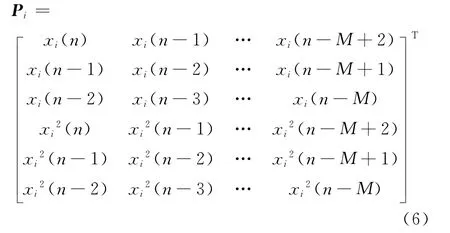
考虑最极端的情形,即真实发射机和欺骗干扰机的功放输入信号矩阵相同,P1=P2,此时两者发射信息完全相同,属于最难识别的情形。则基于上述模型,欺骗干扰的检测问题为:

式中:H0假设接收机接收的信号来自于真实发射机;H1假设接收机接收的信号来自于欺骗干扰机。
采用似然比检测来识别欺骗干扰信号,检测识别准则为:

式中:py|hi,P(y|hi,P),i=1,2分别为真实信号和干扰信号的条件概率密度函数:

将式(9)代入到式(8)中并化简,可得检测器为:

检测错误概率Pe为:

假设接收机等概率地接收真实信号和欺骗干扰信号,则有:

结合式(10)和式(12)可得:

由于H1假设条件下,y=Ph2+v,则式(13)可化简得:

式中:d=h2-h1。
3 实验验证
为了验证上述方法的有效性,一方面,构建了实验平台以获取实测数据来验证检测识别效果;另一方面,将上述方法与基于信号分析手段提取的双谱特征参数[3]识别效果进行对比。
首先,实验使用Maxim公司生产的完全一样的2块MAX2242功率放大器评估板,其输入信号是频率为2.4GHz、功率为0dBm的标准正弦信号。实验平台搭建如图1所示,包括信号发生器、电源、MAX2242评估板和示波器等。示波器采集的输出信号如图2所示,可见2个功放的输出基本一致。采用记忆深度为2的2阶Hammerstein模型建模,得到的功放1和功放2的模型特征参数向量分别为:


图1 实验平台

图2 2个功放在2.4GHz的输出信号
设真实发射机以功放1为其射频前端放大器,欺骗干扰机以功放2作为其射频前端放大器,接收机在自由空间中等概率接收采集到的真实信号和欺骗干扰信号共1 000次。每次数据的样本长度为641,分别对真实信号与干扰信号加入高斯白噪声,设定干噪比(JNR)为30dB,信噪比(SNR)以1dB为步长由-10dB变化至30dB。图3为SNR=30dB、JNR=30dB时真实信号和欺骗干扰的双谱沿径向切面图。图4分别给出了基于射频功放非线性建模和基于信号双谱特征参数的欺骗干扰识别结果,其中本文采用的是统计检测识别方法,而基于信号双谱特征参数方法采用的是BP神经网络,神经网络输入层数为256,中间层数为20,输出层数为2,训练次数为15 500,训练目标设为0.001。由图4可见,基于射频功放非线性建模的欺骗干扰识别方法在SNR=15dB左右错误率趋近于零,基于双谱特征参数的识别方法则需要在SNR=25dB时错误率才逼近零。可见,本文方法在同等情况下,较传统信号特征提取的方法识别性能有明显改善。

图3 真实信号和欺骗干扰双谱特征

图4 本文算法和双谱特征识别性能曲线
进一步考查基于射频功放非线性建模的欺骗干扰识别方法和干噪比(JNR)的关系,实验环境和图3实验环境相同。检测识别错误概率和SNR、JNR的关系如图4所示。可知,JNR越大越容易检测出欺骗干扰信号,识别欺骗干扰的性能越好。在一定JNR条件下,识别错误概率随SNR的增加呈下降趋势,但识别错误概率曲线并不总是能够趋近于零。

图5 检测识别错误概率和信噪比、干噪比的关系
4 结束语
由于制造工艺的限制,实际中射频前端的功率放大器存在互调失真等非线性因素,这些因素造成每个功率放大器具有微小差异,可以将这些微小差异作为识别欺骗干扰的“指纹”特征。本文从发射机和干扰机硬件结构出发,提出了基于功率放大器非线性模型识别欺骗干扰的方法。使用Hammerstein模型对功率放大器进行建模,得到放大器的特征参数向量。然后基于该特征参数向量,采用似然比检测识别欺骗干扰,并且将上述方法与基于信号双谱特征参数的神经网络识别方法进行性能对比。最后实验结果表明:在相同条件下,本文提出的检测识别方法优于基于信号双谱特征参数的识别方法;JNR越大,欺骗干扰信号越容易被识别;在一定JNR条件下,识别错误概率随SNR的增加呈下降趋势,但识别错误概率曲线并不总是能够趋近于零。
[1]Olivier K,Cilliers J E,Du Plessis M.Design and performance of wideband DRFM for radar test and evaluation[J].Electronics Letters,2011,47(14):824-825.
[2]Molchanov P O,Astola J T,Egiazarian K O,et al.Target classification by using pattern features extracted from bispectrum-based radar Doppler signatures[A].Radar Symposium (IRS),2011Proceedings International.IEEE[C].Kharkov,2011:791-796.
[3]Chen V C,Miceli W J,Himed B.Micro-Doppler analysis in ISAR-review and perspectives[A].Radar Conference-Surveillance for a Safer World,2009.RADAR.International.IEEE[C].Washington DC,2009:1-6.
[4]Psiaki M L,O'Hanlon B W,Bhatti J A,et al.Civilian GPS spoofing detection based on dual-receiver correlation of military signals[J].Proceedings of The Institute of Navigation GNSS(ION GNSS 2011),2011,20(23):245-261.
[5]Nielsen J,Broumandan A,Lachapelle G.Gnss spoofing detection for single antenna handheld receivers[J].Navigation,2012,58(4):335-344.
[6]Ppolito S J,Kandasamy S,Kalantar-Zadeh K,et al.Comparison between conductometric and layered surface acoustic wave hydrogen gas sensors[J].Smart Materials and Structures,2006,15(1):126-131.
[7]Guo B,Wen G.Periodic time-varying noise in currentcommutating cmos mixers[J].Progress in Electromagnetics Research,2011,117(13):283-298.
[8]Mkadem F,Boumaiza S.Physically inspired neural network model for RF power amplifier behavioral modeling and digital predistortion[J].IEEE Transactions on Microwave Theory and Techniques,2011,59(4):913-923.
[9]Yeh H C,Chiong C C,Aloui S,et al.Analysis and de-sign of millimeter-wave low-voltage CMOS cascode LNA with magnetic coupled technique[J].IEEE Transactions on Microwave Theory and Techniques,2012,60(12):4066-4079.
[10]Li L,Ji H B,Jiang L.Quadratic time-frequency analysis and sequential recognition for specific emitter identification[J].IET signal processing,2011,5(6):568-574.
[11]Polak A C,Dolatshahi S,Goeckel D L.Identifying wireless users via transmitter imperfections[J].IEEE Journal on Selected Areas in Communications,2011,29(7):1469-1479.
[12]Krzy˙zak A,Partyka M A.Global identification of nonlinear Hammerstein systems by recursive kernel approach[J].Nonlinear Analysis:Theory,Methods &Applications,2005,63(5):e1263-e1272.
[13]Xu Y,Wang J,Zhu X,et al.Dynamic extended Hammerstein model of RF power amplifiers for digital predistortion[A].Microwave Integrated Circuits Conference(EuMIC)[C].Manchester,2011:276-279.
[14]Dewhirst O,Simpson D M,Angarita N,et al.Wiener-Hammerstein parameter estimation using differential evolution[J].Proc.of Biosignals,2010,44(7):271-276.

