一种基于滑动滤波的数字AGC应用
吕余清,张松柏
(船舶重工集团公司723所,扬州225001)
0 引 言
自动增益控制(AGC)是根据接收信号强度变化,自动地调整接收机前端增益,使接收到的信号强度保持不变的过程[1]。传统接收机多采用模拟电路来实现,利用充放电电路控制负反馈的反馈增益,实现对接收机增益的控制,但是存在控制精度差、收敛速度慢、灵活性小等缺点。现代接收机多采用数字下变频技术,中频信号被数模转换器(DAC)采样,变成数字信号,这为数字AGC的应用提供了前提条件,又因为数字AGC不存在上述模拟AGC的不足,所以数字AGC已逐渐成为接收机AGC控制的主流方法。本文论述了一种基于滑动算法的数字AGC的实现,具有算法简练、控制精度高、收敛速度快、可移植性强等特点。
1 工作过程
图1所示为数字AGC的过程框图。高频信号si经接收机前置放大、数控衰减、中频检波与放大后,变为中频信号so,so经中频模数转换器(ADC)变换为数字信号,再经数字下变频转换为基带信号,AGC数据采样模块对下变频后的基带信号取模值,模值信号经AGC滤波算法得到控制数控衰减器的衰减控制码,直接作用于数控衰减器,控制接收机接收增益[2]。在实际环境中,si信号不可能总是保持恒定的幅值,如果数控衰减器为一恒定的衰减量,则si信号变化后,so信号亦会朝着si信号变化的方向而变化。当AGC过程起效,数控衰减器受控后,情况就不一样了。当si信号变大时,衰减控制码变大,数控衰减器衰减量变大,接收机增益减小,so信号保持不变;当si信号变小时,衰减控制码变小,数控衰减器衰减量变小,接收机增益增大,so信号亦保持不变;因此,不管si信号变大还是变小,由于数控衰减器的实时调节作用,so信号不会随输入变化而急剧变化,而是保持在期望值附近,从而实现了AGC控制目的。

图1 数字AGC过程框图
2 工作原理
从图1抽象出AGC的数学模型如图2所示,Si为输入,So为输出,E为收敛期望值,α为滑动滤波系数,e为期望值与输出的差值(量纲为分贝),A为受控的衰减器衰减量。
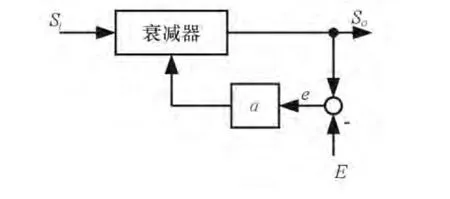
图2 数字AGC数学模型
由图2可知,这是一个反馈控制系统[3],受控量为衰减器的衰减A,控制量为e,当e>0时,说明输出值比期望值小,衰减器衰减量A变小,从而使输出朝增大的方向变化;当e<0时,说明输出值比期望值大,衰减器A衰减量增大,从而使输出朝减小的方向变化;当e=0时,说明输出值与期望值相等,受控量A衰减量维持不变。
具体实现原理可由以下公式描述:
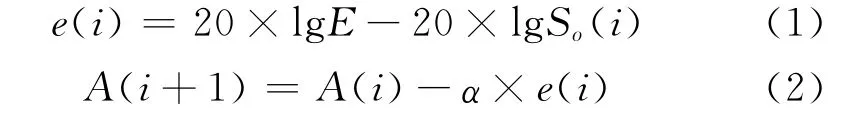
由公式(1)和(2)可知,当输出与期望值一致时,e(i)=0,因而控制的A(i+1)衰减量等于上次A(i)的衰减量,维持不变;当输出比期望值小,e(i)>0,因而控制的A(i+1)衰减量等于上次A(i)的衰减量减去一个正值,当前衰减量比上次衰减量减小;当输出比期望值大,e(i)<0,因而控制的A(i+1)衰减量等于上次A(i)的衰减量减去一个负值,当前衰减量比上次衰减量增大。
由公式(1)和(2)可得:

AGC输出为:
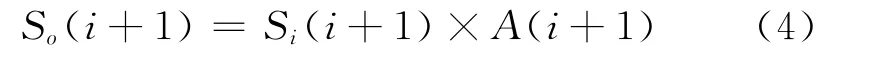
由以上公式可以看出,由于采用了滑动滤波,每次计算当前衰减量A时,系统只需要知道当前的期望值与输出的差值即可,不需要存储过多的历史数据就可以得到控制量,因而计算简便,易于工程实现。由公式(3)还可以知道,该算法的响应速度与α值大小相关,当α较大时,响应速度快,但是过冲大,收敛后幅值平稳度不高;当α较小时,过冲小,收敛后幅值平稳度高,但是响应速度慢。正常工作时,α取0~1之间的值,具体大小可根据工程实际试验得出。
3 工作流程
图3是基于滑动滤波算法的数字AGC的数字信号处理(DSP)程序流程图,其中AGC样本为接收机正交数字下变频后I、Q两路信号的模值,在本应用中采用了将一定范围内数据取最大值的方法获得供比较的输出So,这样可以保守地保证在AGC作用范围内,输出数据均不会超出幅度范围。
根据上一节对数字AGC工作原理的分析,知道α的值的大小对系统的性能影响很大,所以在实际工程实现的过程中,需要根据实际情况确定α值的大小。本设计应用中为了兼顾响应速度、过冲、稳态的平稳度,采用了变α的方法,即在不同阶段使用不同的α值,准则是根据期望值与输出的差值e的绝对值大小来决定α的大小。当e的绝对值较大时,说明输出值与期望值相差较大,此时的主要矛盾是响应速度,所以在这个阶段采用较大的α值,使其快速逼近期望值;当e的绝对值变小后,说明输出值与期望值相差已经变小,此时的主要矛盾是收敛后的平稳度,所以在这个阶段采用较小的α值,使其在期望值处起伏较小。
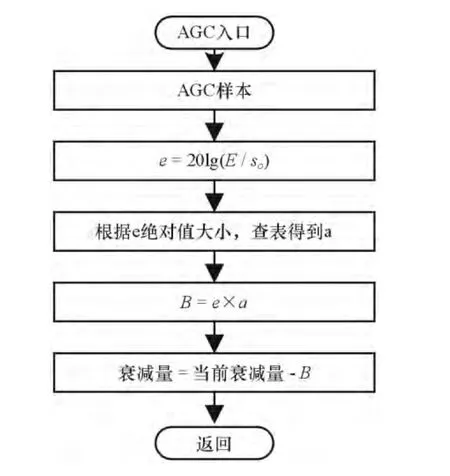
图3 AGC工作流程图
4 仿真实验
4.1 功能仿真
仿真参数:输入信号为幅度-100~+100,以0为中心,起伏变化的正弦信号(中频信号);起伏模型符合Swerling2型[4];回波幅度服从瑞利分布;滤波系数α为0.01;期望值为60。
经过Matlab仿真后的输入与输出波形对比如图4所示,输入信号幅值起伏变化时,对输出影响较小,输出信号的幅值没有跟随输入信号幅值起伏而起伏,而是一直稳定在期望值60。
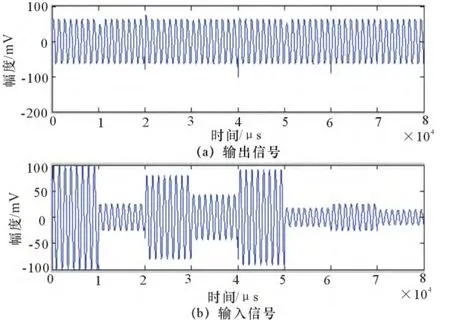
图4 AGC输入信号与输出信号
4.2 响应速度仿真
仿真参数:输入信号为幅值为50的阶跃信号源,α分别为0.1、0.5、0.8和1.5,期望值为10。
经过Matlab仿真后的响应曲线如图5所示,从图中可以看出,随着α的增大,响应曲线越来越陡,即对相同输入,输出值收敛速度越来越快,但是当α>1后,输出曲线出现过冲,且收敛过程中振荡时间变长,最终的收敛时间反而没有α较小时快。
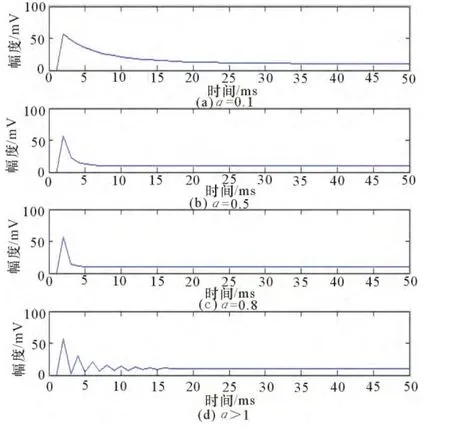
图5 响应速度与滤波系数的关系
5 结束语
通过以上分析,基于滑动滤波的数字AGC不依赖过多的样本存储,算法简单;根据不同的实际应用,调节滤波系数α,便可实现对收敛速度快、稳定度等指标的调节;在雷达应用中,对于幅度起伏快速的目标回波,收敛快速,对回波幅度闪烁起到很好的抑制作用。
[1]丁鹭飞,耿富录.雷达原理[M].西安:西安电子科技大学出版社,1997.
[2]Mahafza Bassem R,Elsherbeni Atef Z.雷达系统设计MATLAB仿真[M].朱国富,黄晓涛,黎向阳,李悦丽译.北京:电子工业出版社,2009.
[3]韩尧,秦开宇,彭启琮.基于数字补偿的实时自动增益控制技术研究[J].电子科技大学学报,2007,36(1):79-81.
[4]喻斌,陈军波,李青侠.数字 AGC的分析和设计[J].桂林电子工业学院学报,2003(5):35-37.

