二重积分的重要函数法模拟

王洪涛，李满枝，沈有建

(海南师范大学数学与统计学院，海南海口571158)

引 言

蒙特卡罗方法是计算多重积分常用的一种算法，是以随机模拟和统计试验为手段，从随机变量概率分布中，通过选择随机数方法产生一种符合该随机变量概率分布特性的随机数值序列，作为输入变量序列进行特定的模拟试验、求解的方法。[1]蒙特卡罗方法一般都是将抽样点均匀分布在积分区域中，假如我们可以将抽样点分布集中在“最重要的”区域(对结果贡献最多的区域)中，而不是均匀分布于某一范围内，蒙特卡罗方法效率便提高了，使用这一概念于蒙特卡罗抽样过程中，叫做“重点抽样”，对于某区域重要性进行衡量的函数叫做“重要函数”，这种减少方差的模拟试验法为重要抽样法，也称为相似密度抽样法。

一 重要函数法计算二重积分数值算法

积分都可以看作是某个随机变量的数学期望。因此，在利用蒙特卡罗法计算二重积分的时候，采用了这个随机变量算术平均值来作为其近似值。[3][4]

定理1[2][3][4]对于二重积分dy，设f(x，y)为区域D上的有界函数，

1)在所求积分区域D上构造一个概率密度函数 g(x，y)，满足条件

2)令

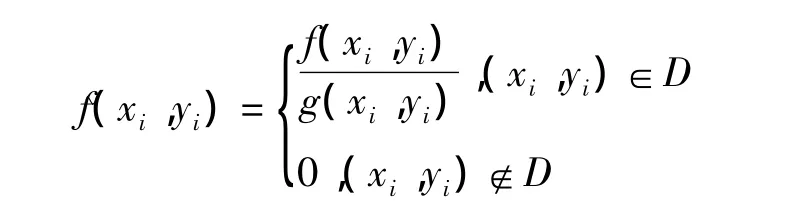
3)(xi，yi)，i=1，2，…，n 是以 g(x，y)为概率密度的随机数列，当n充分大时，

则

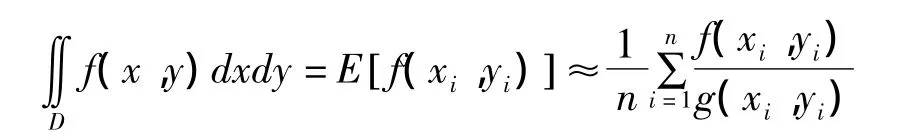
在定理1中，若取 g(xi，yi)=cf(x，y)，c=时，计算方差为零，即方差最小。g(x，y)=cf(x，y)称为有利密度函数或重要函数，以 g(x，y)为概率密度的随机变量(xi，yi)，i=1，2，…，n称为有利随机数，这样得到方差最优的蒙特卡罗算法。

定理2[5][6]设 g(x，y)为某二维概率密度函数，D为一平面区域，满足(xi，yi)，i=1，2，…，n 是区域 D 上的均匀分布随机向量，zi为[0，1]上的均匀分布随机变量，(xi，yi)与 zi相互独立。取常数 α＞0，使 αg(x，y)≤1，则(xi，yi)在 αg(x，y)≥zi条件下的条件概率密度函数为 g(x，y)。

一场看似无法避免的悲剧，却又消弭于无形之中，而用的方法却异常简单，似不合情理，但仔细一想，却又合情合理，回过头来一看，这个故事所体现的正是一种简单的智慧。人生的实质就是在不断地解决问题，而解决问题的方法却有千千万万，就如同那沙滩上的沙砾，一望无际。但总起来说只有两类：将问题简单化或复杂化。面对难题，智者只是将思维稍稍转了一下弯，绕过障碍，就能取得“山重水复疑无路，柳暗花明又一村”的效果；而普通人却是向这个难题发起无用的冲击，最后身陷绝境，进退不得，抱憾终生。

二 具体算法及算例

(一)根据被积函数f(x，y)估算c值，得到概率密度函数 g(x，y)=cf(x，y);

(二)在区域D内产生以g(x，y)为概率密度函数的二维随机数(xi，yi)，i=1，2，…，n;

(三)计算 f(xi，yi)(i=1，2，…，n);

应用重要函数法计算积

为了便于进行结果对比，应用线性同余法产生1000个均匀随机数，每100个随机数计算一次计算结果。由，

f(x，y)=x2+y2，x∈[－1，1]，y∈[0，3]，在积分区域中选取三个点分别应用泰勒公式展开，应用重要函数法进行计算，并对比计算结果。

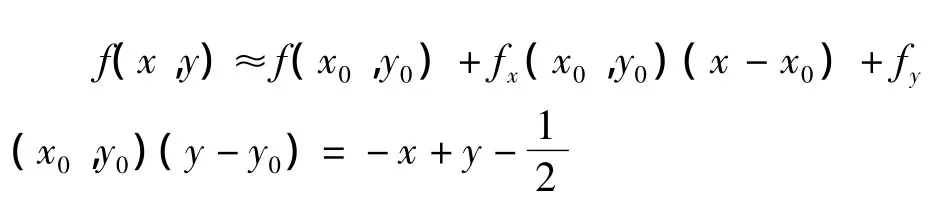
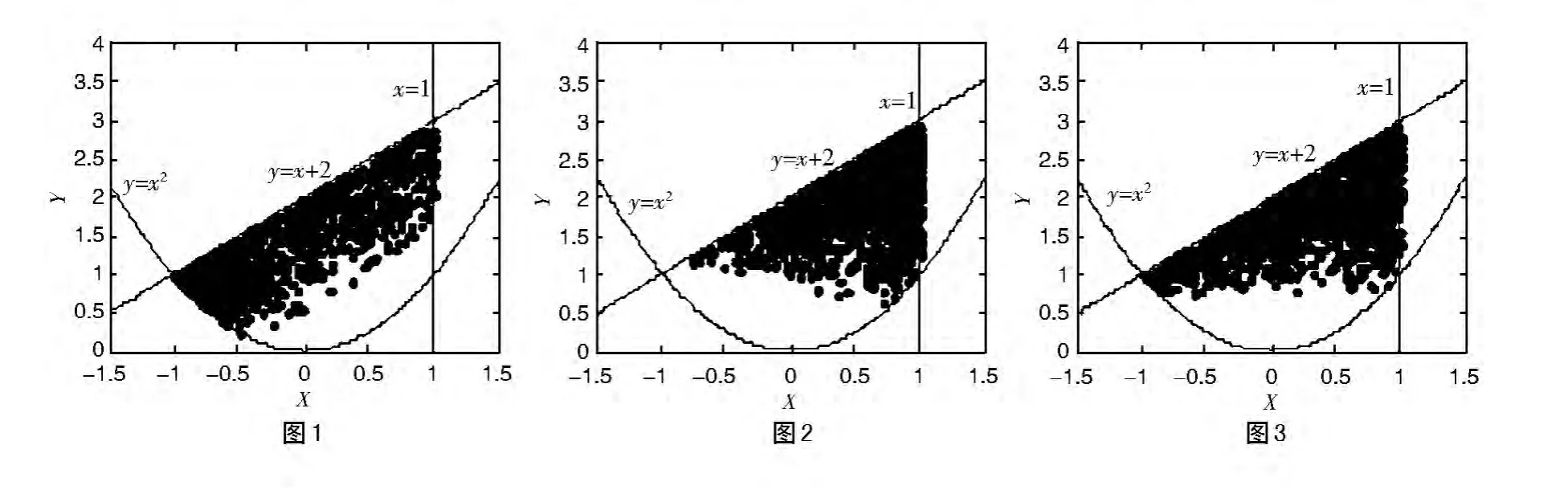
根据定理2，由 αg(x，y)≤1，因为 max[g(x，，令α=0.5即可满足条件，产生以g(x，y)为概率密度函数的二维随机数(xi，yi)，随机点分布图见图1。

积分计算公式为

2.(x0，y0)处展开得

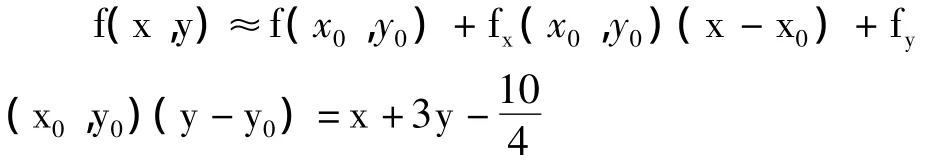
根据定理 2，由 αg(x，y)≤1，因为 max[g(x，，令 α=0.5即可满足条件，产生以 g(x，y)为概率密度函数的二维随机数(xi，yi)，随机点分布图见图2。

积分计算公式为

3.在(x0，y0))处展开得

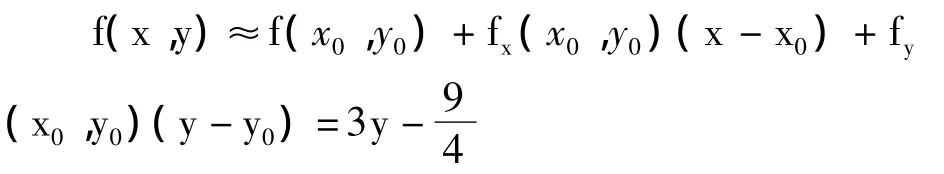
根据定理 2，由 αg(x，y)≤1，因为 max[g(x，，令 α=0.5即可满足条件，产生以 g(x，y)为概率密度函数的二维随机数(xi，yi)，随机点分布图见图3。

积分计算公式为

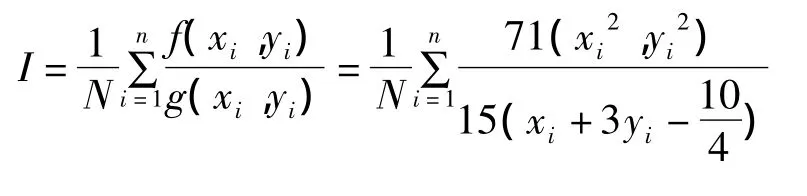
下表给出上述三种计算结果。其中，积分理论值为 I=7.50476。

不同点的展开计算结果

结 论

(一)应用重要函数法计算二重积分难度较大，尤其是估计值十分繁琐。

(二)在积分区域中选取不同的点，分别应用泰勒公式展开函数得到不同结果，计算效果相差很大，样本点在重要区域分布图也不一样;若在不合适点展开函数得到的结果误差很大，严重失真。

(三)在积分区间中点(0，1.5)展开函数得到的结果最理想。

(四)根据算法构造和计算结果比较，重要函数法的结果受到取点位置影响较大。

[1]徐钟济.蒙特卡罗方法[M].上海:上海科学技术出版社，1985.

[2]尹增谦，管景峰.蒙特卡罗方法及应用[J].物理与工程，2002(3).

[3]刘辉玲，叶锋.计算多重积分的均匀随机数蒙特卡罗法的实现[J].电脑知识与技术，2008(8).

[4]黎锁平.运用蒙特卡罗方法求解随机性问题[J].甘肃工业大学学报，2001(2).

[5]李满枝，王洪涛，苗俊红.二重积分的Monte－Carlo数值仿真[J].计算机仿真，2011(5).

[6]李满枝，王洪涛.蒙特卡罗积分计算[M].海口:海南出版社，2011.