基于自适应量子遗传算法的分数阶控制器参数整定

杨 勇，李 荣，张 君

(南京工程学院 能源与动力工程学院，江苏 南京 211167)

0 引言

分数阶微积分将整数微积分的微分、积分阶次推广到了任意阶次，扩展了整数阶微积分的描述能力。分数阶微积分的数学模型，可以更准确地描述实际系统的动态响应，提高对于动态系统的设计、表征和控制能力[1～4]。

PID是控制系统中应用最广泛、技术最成熟的控制方法，由于其结构简单，鲁棒性强，操作简单，被广泛应用于冶金、电力和机械等工业过程中，具有很强的生命力。相比于整数PID，分数阶PIλDμ是整数PID的扩展，积分阶次λ和微分阶次μ的引入使得分数阶PIλDμ控制器具有更灵活的结构、更强的鲁棒性和更好的抗扰动能力，但同时，由于分数阶微积分模块建模复杂且控制器需要整定参数较多，使得 PIλDμ参数整定更加困难[5～9]。一些学者从时域[1]、频域[5]等角度分析分数阶系统，提出了相应的参数整定方法，但计算过程较繁琐。

量子遗传算法[10～15](quantum genetic algorithm，QGA)是一种基于量子计算原理的概率优化方法，它以量子计算的一些概念和理论为基础，用量子位编码来表示染色体，以量子门更新来完成进化搜索，具有种群规模小、收敛速度快和全局寻优能力强的特点。在量子门更新时，旋转角的大小直接影响量子遗传算法的优化结果，但是，在量子遗传中旋转角是固定的，鉴于这种情况，本文提出一种自适应量子遗传算法(adaptive quantum genetic algorithm，AQGA)，使得个体根据自己的适应度，自适应改变旋转角，以改善量子遗传算法的优化精度和收敛速度。同时，将该方法应用于分数阶PIλDμ控制器参数整定中，针对循环流化床主汽温分数阶系统设计PIλDμ控制器，通过仿真实验验证该方法的有效性。

1 自适应量子遗传算法

1.1 量子比特编码

量子遗传算法中，采用量子比特的概率幅(α，β)来编码染色体，以一个量子比特来存储和表达一个基因，一个量子位可能处于|1〉或|0〉，或者处于|1〉和|0〉之间的中间态，表示为

式中:α，β是两个常数，且满足:

此时该基因所表达的不再是某一确定的信息，而是包含所有可能的信息。

1.2 量子门更新

量子遗传算法中，对信息的基本操作由量子门来实现。其更新过程为

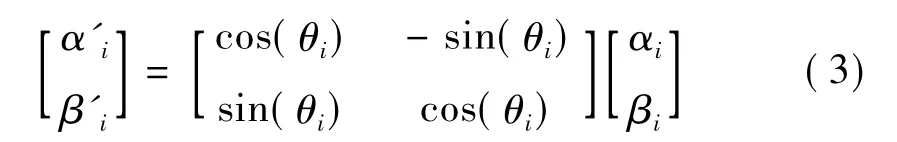
根据式(3)可得:

将(αi，βi)T，( α 'i，β'i)T看为是直角坐标系中的两个向量，则两个向量之间的夹角θ满足式(5):

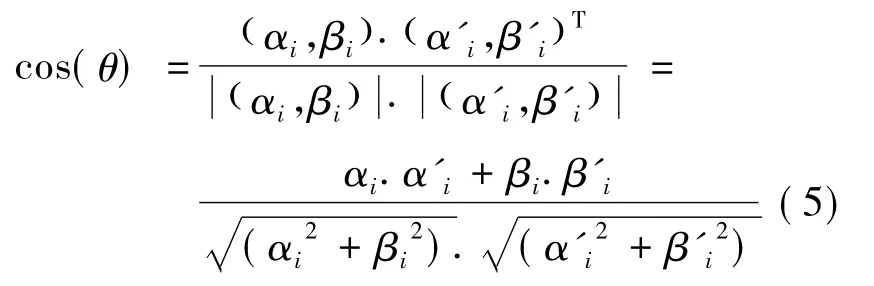
将式(2)、(4)带入式(5)，并整理后可得:

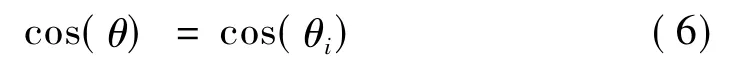
从式(6)可看出量子门更新相当于将原量子旋转θi来实现量子演化的，如图1所示。

图1 量子更新原理图Fig．1 Schematic diagram of quantum update

因此，在量子遗传算法中，量子门的设计直接影响量子遗传算法的性能，量子旋转门的调整策略如表1所示。

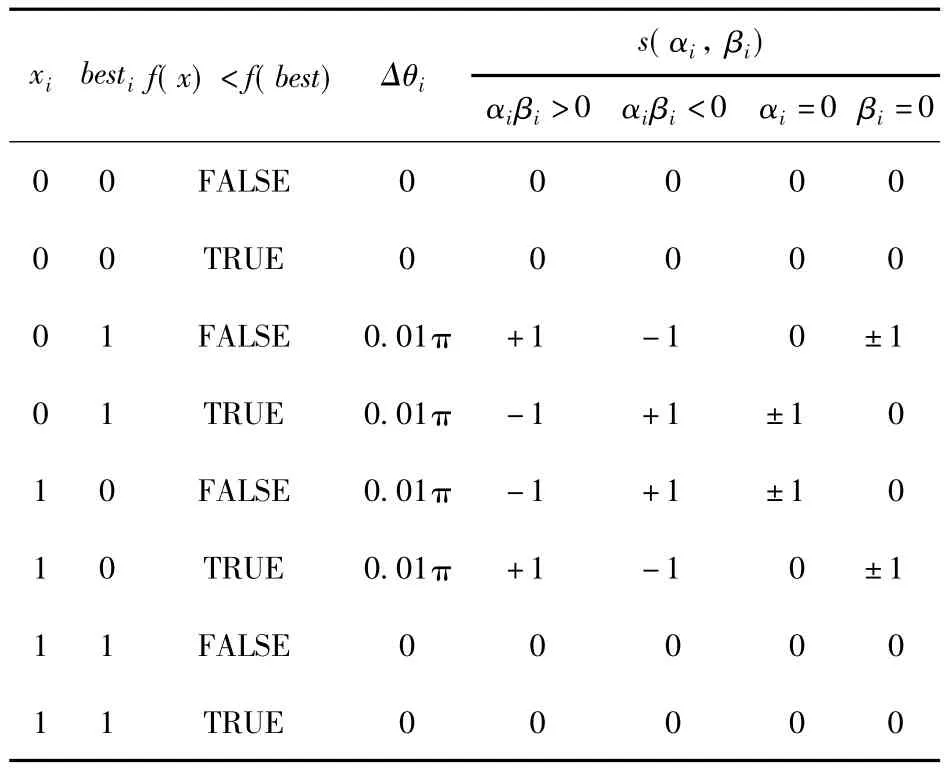
表1 量子旋转门调整策略Tab.1 Quantum revolving door adjustment strategy

表1中，xi，besti分别表示当前解x与最优解best染色体的第 i位;f(x)为目标函数;s(αi，βi)为旋转方向;Δθi为旋转角的幅值;实际旋转角θi为s(αi，βi) × Δθi。

该调整策略根据个体的适应度与种群最优个体适应度的比较结果调整个体中的量子比特，使概率幅(αi，βi)向着更优目标函数值的方向演化，保证算法收敛到具有更高适应度的染色体。

1.3 自适应量子遗传算法

量子遗传算法中，旋转角θi幅值影响算法的收敛速度，若θi太小，则算法收敛较慢;若θi太大，则算法容易陷入早熟[11]。表1的调整策略中，θi是一个固定值，但在实际中，若当前值离最优值较远时，希望取较大的θi值，使之迅速向最优值靠近，加速算法的收敛速度;若当前值离最优值较近时，希望取较小的θi值，以避免算法早熟。基于上述情况，本文提出旋转角度随着个体适应度的变化而自动调整的策略。旋转角度幅值的调整策略如式(7):

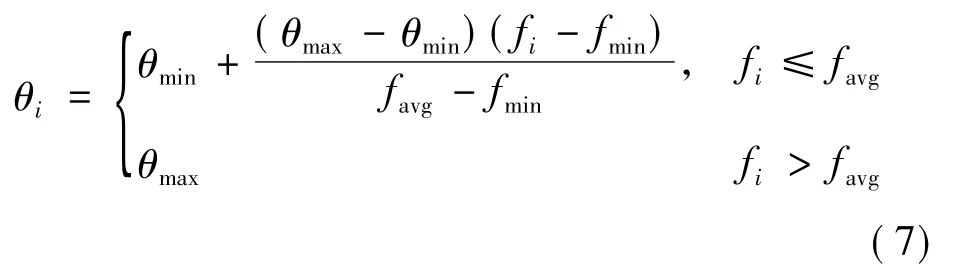
式中:θmax和 θmin分别代表 θ的最大和最小值;fi为个体当前的目标函数值;favg和fmin分别为当代个体的平均目标函数值和最小目标函数值。

1.4 自适应量子遗传算法流程

(1)确定进化代数、种群大小，染色体编码长度，优化参数个数及范围等;

(2)随机产生初始种群G(1);

(3)对G(1)中的个体进行测量并解码，得到相应的实数解;

(4)利用适应度函数评价G(1)的每个个体，记录最优个体以及其适应度;

(5)判断是否满足算法结束条件，若满足，则输出最优解，否则，转到步骤(6);

(6)对种群G(t)中的每个个体实施一次测量、解码，得到相应的实数解;

(7)计算G(t)中个体的适应度;

(8)根据式(7)计算个体的旋转角幅值，根据表1计算量子旋转的方向，从而得到个体的旋转角，然后利用量子旋转门更新群体，得到下一代种群G(t+1);

(9)令 t=t+1，返回步骤(5)。

1.5 算法性能测试

De Jong[16]函 数 F = 100 (x21－ x2)2+(1 － x1)2，其中(－2．048≤xi≤2．048，i=1，2)，De Jong函数是一个二维函数，在整个解域中只有一个全局最小点 f(1，1)=0，该函数虽然是单峰值函数，但它却是病态的，难以进行全局优化。为此本文分别采用量子遗传算法和自适应量子遗传算法进行寻优，两种算法的参数设置如表2:

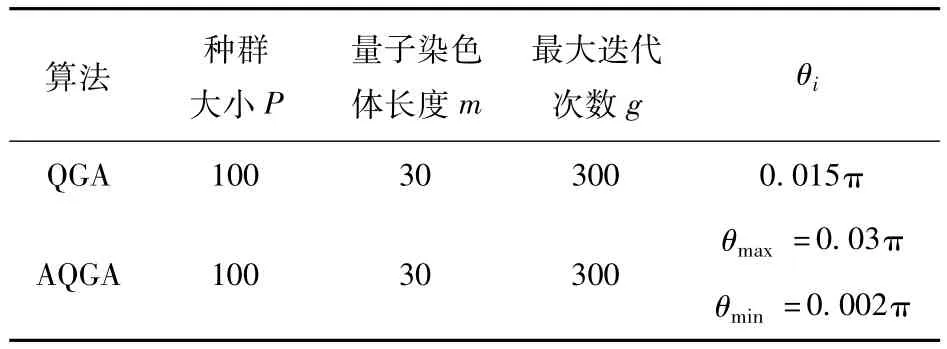
表2 量子遗传和自适应量子遗传参数设置Tab.2 Parameter settings of QGA and AQGA

其中，量子遗传算法转变异角θi的幅值保持0.015π不变，而自适应量子遗传算法中，旋转变异角θi的幅值根据式(7)自适应改变;两种算法的终止条件为最优值保持不变超过10代或者达到最大迭代次数。

分别对该函数优化100次，优化结果如表3所示，从表3可以看出，量子遗传算法在旋转角采用自适应策略后，优化精度和收敛速度(平均迭代次数)有明显提高。

表3 优化结果Tab.3 Optimization results

2 分数阶微积分以及分数阶控制器

2.1 分数阶微积分定义

分数阶微积分是任意阶微分和积分的理论，它与整数阶微积分是统一的，是整数阶微积分的推广。分数阶微积分算子的定义如(8)式:

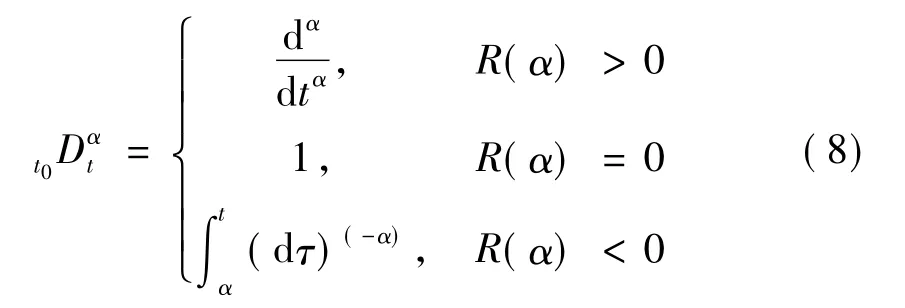
式中:t和t0为操作算子的上、下限;a为微积分阶次，可取复数内任意值，本文假设它在实数范围内。

Grünwald-Letnikov分数阶微积分定义是分数阶控制中最广泛应用的分数阶微积分定义，对连续可导函数f的α阶微积分定义如(9)式:

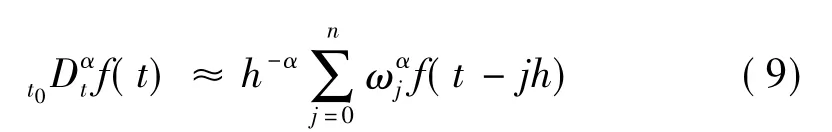
式(9)统一定义了分数阶微分和积分，α＞0时，表示分数阶微分，α＜0时，表示分数阶积分。

2.2 分数阶控制器

分数阶PIλDμ控制器是传统整数阶PID控制器概念的推广，其包括一个积分阶次λ和一个微分阶次μ，而且积分阶次λ和微分阶次μ可以不是整数的形式。分数阶PIλDμ控制器的结构示意图如图2。

图2 分数阶PIλDμ控制器的结构示意图Fig．2 Schematic diagram of PIλDμ

分数阶控制器PIλDμ的传递函数:

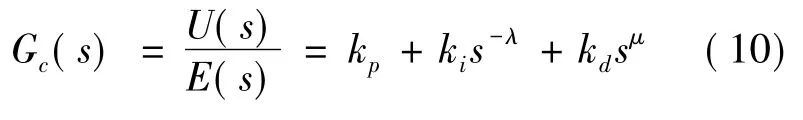
式中:kp为比例增益;ki为积分增益;kd为微分增益;λ为积分阶次;μ为微分阶次。λ，μ＞0且为实数。当λ和μ取不同值时，分数阶控制器PIλDμ有不同的结构。

(1)当λ=0和μ=0时，Gc(s)=kp，此时分数阶控制器为常规比例P控制器;

(2)当 λ =1和 μ=0时，Gc(s)=kp+ki/s，此时分数阶控制器为整数阶PI控制器;

(3)当 λ =0和 μ=1时，Gc(s)=kp+kis，此时分数阶控制器为整数阶PD控制器;

(4)当 λ=l和 μ=1时，Gc(s)=kp+ki/s+kds，此时分数阶控制器为常规的PID控制器。

可见，所有的整数阶PID控制器都只是分数阶PIλDμ控制器的特殊情况。因此，对于分数阶PIλDμ控制器的研究也更加的复杂。

3 循环流化床主汽温分数阶控制器设计

3.1 对象描述

文献[2]中建立了减温水流量扰动下，循环流化床主汽温度对象的分数阶模型，并指出其精确度要高于整数阶模型。其分数阶模型为

在减温水单位阶跃扰动下，主汽温度的输出响应如图3所示。

图3 循环流化床主汽温对象单位阶跃响应曲线Fig．3 Unit-step response of main steam temperature of circulating fluidized bed boiler

由图3可看出该对象是一个具有大滞后、大惯性的系统，属于热工中较难控制的对象。

3.2 分数阶控制器优化

3.2.1 性能指标函数

分数阶控制器参数整定的问题就是确定kp，ki，kd，λ，μ这5个参数的组合是某一性能指标达到最优。为了整定控制器参数，本文选取ITAE作为个体适应度的评价指标，ITAE计算如(12)式:

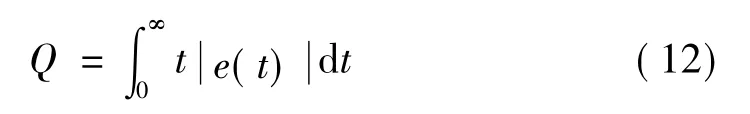
3.2.2 分数阶系统数值计算

为了计算性能指标，需要对分数阶控制系统进行数值计算。本文采用具有一定记忆长度的分数阶微积分算子进行分数阶系统计算，根据Grünwald-Letnikov定义，在误差允许的范围内，指定记忆长度L，忽略较早的数据点[7]，得到:

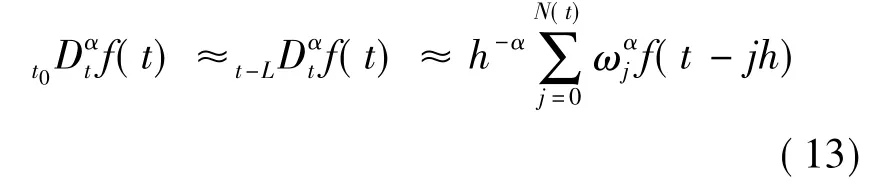
对于分数阶微分方程:

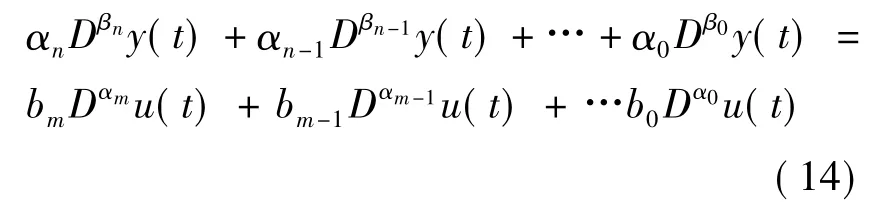
利用式(13)近似方程(14)中的微分算子，将(14)转化为离散时间序列 tk(k=1，2，3，…)上的离散方程:

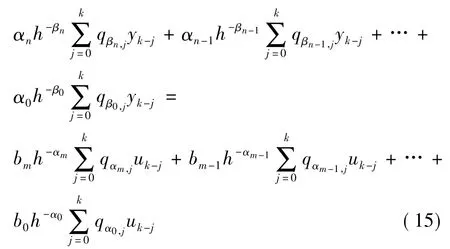
计算得:

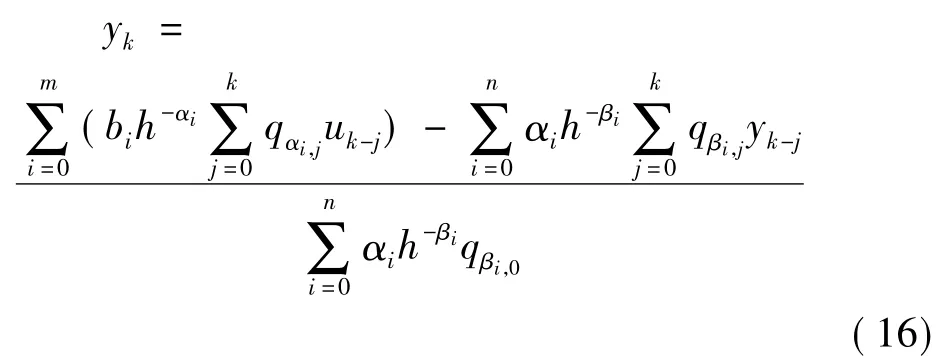
式中:y0=0;y1=0;uk为输入序列;

3.3 系统仿真

3.3.1 量子遗传与自适应量子遗传对比

分别采用量子遗传与自适应量子遗传算法优化分数阶PIλDμ控制器，为了防止控制量的变化超过合理的范围，本文对控制器输出进行了限幅，设置控制器输出范围为[－30，30]。优化结果以及控制系统性能分别如表4和表5所示，给定值单位阶跃扰动时，系统的输出对比曲线以及控制器输出对比曲线分别如图4和图5所示。

表4 PIλDμ参数优化结果Tab.4 Optimization results of PIλDμ parameters

表5 控制系统性能Tab.5 Performance of control system

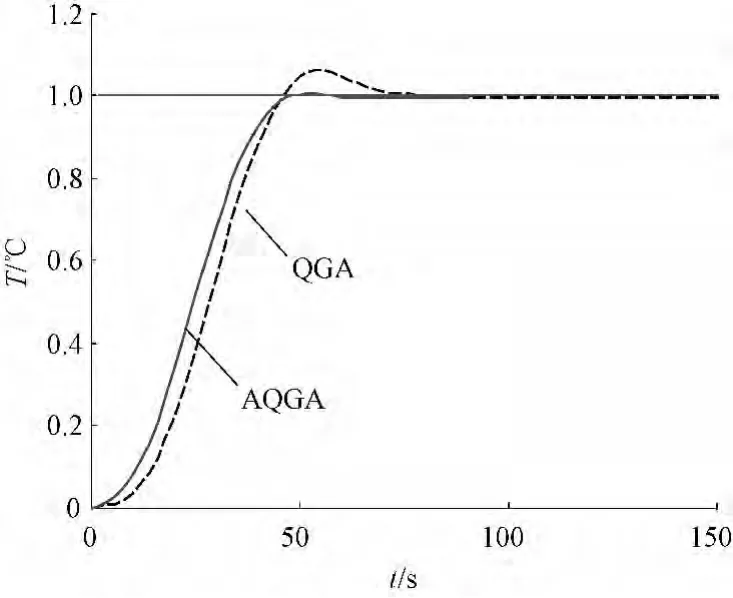
图4 循环流化床主汽温控制系统的单位阶跃响应Fig．4 Unit-step response of main steam temperature of circulating fluidized bed boiler system

图5 系统控制器输出曲线Fig．5 Output curves of the controller

从图4和表5可以看出，采用AQGA优化的分数阶控制系统调节速度快，调节时间短，调节过程中几乎无超调，与QGA优化的控制系统相比，具有更优的控制品质。

3.3.2 系统鲁棒性

将对象的比例增益分别取 8，9，10.372 5，12，14时系统的单位阶跃响应如图6所示。

从图6分析可以得到以下结论:

(1)在比例增益发生较大变化时，系统仍能达到较好的控制性能，系统具有较强的鲁棒性;

(2)当比例K减小时，系统的超调量增大，系统的上升时间变快;当K增大时，与K减小时相反。

图6 K值变化控制系统的单位阶跃响应Fig．6 Unit-step response of the system when K of the object model is changed

4 结论

本文在量子遗传算法的基础上，提出了一种旋转角随个体适应度而自适应变化的策略，有效克服了量子遗传算法中旋转角相对固定的缺点，提高了算法的收敛速度和优化精度。

分数阶PIλDμ控制器由于分数阶微积分模块建模复杂且控制器需要整定参数比较多，使其参数整定比较困难。本文将分数阶PIλDμ控制器参数整定问题转化为参数优化问题，采用自适应量子遗传算法对循环流化床分数阶系统设计分数阶PIλDμ控制器，仿真结果验证了该方法的有效性，为PIλDμ控制器参数整定提供了一个新的途径。

[1]薛定宇，赵春娜．分数阶系统的分数阶PID控制器设计[J]．控制理论与应用，2007，24(5):771－775

[2]Wang D F，Wang X Y，Han P．Identification of Thermal Process Using Fractional-Order Tranfer Function Based on Intelligent Optimization[C]．Proceedings of MESA 2010:498－503

[3]Ahn H S，Bhambhani V，Chen Y Q．Fractional-order integral and derivative controller design for temperature profile control[C]．Chinese Control and Decision Conference，Yantai，2008．

[4]Podlubny I，Fractional-order systems and PIλDμcontrollers[J]．IEEE Transactions on Automatic Control，1999(44):208－214．

[5]曾庆山，曹广益，王振滨．分数阶PIλDμ控制器的仿真研究[J]．系统仿真学报，2004，16(3):465－469

[6]李大字，刘展，靳其兵，等．分数阶控制器参数整定策略研究[J]．系统仿真学报．2007，19(19):4402－4406

[7]严慧．分数阶 PIλDμ控制器的设计及数字实现[D]．南京:南京航空航天大学，2007．

[8]王东风，王晓燕，韩璞．锅炉－汽轮机系统的分数阶控制器的设计[J]．中国电机工程学报，2010，30(5):113－119

[9]杨勇，王东风，焦嵩鸣．基于混沌PSO的循环流化床汽温系统分数阶控制[J]．华北电力大学学报，2011，38(4):62－67

[10]曾成，赵锡均．改进量子遗传算法在PID参数整定中应用[J]．电力自动化设备，2009，29(10):125－127

[11]董泽，黄宇，韩璞．量子遗传算法优化RBF神经网络及其在热工辨识中的应用[J]．中国电机工程学报，2008，28(17):99－103

[12]王凌，吴昊，唐芳，等．混合量子遗传算法及其性能分析[J]．控制与决策，2005，20(2):156－158

[13]焦嵩鸣，韩 璞，黄 宇，等．模糊量子遗传算法及其在热工过程模型辨识中的应用[J]．中国电机工程学报，2007，27(5):87－91

[14]Yang Junan．Research of quantum genetical agorithm and its application in blind sourcese paration[J]．Journal of Electronics(China)，2003，20(1):62－68．

[15]Talbi H，Draa A，Batouche M．A new quantum inspired genetic algorithm for solving the travelling salesman problem[C]．2004 IEEE International Conference on Industrial Technol-ogy，Tunisia，2004．

[16]于洋，查建中，唐晓君．基于学习的遗传算法及其在布局中的应用[J]．计算机学报，2001，24(12):1242－1249