电力负荷区间预测的集成极限学习机方法
李知艺,丁剑鹰,吴 迪,文福拴
(1.浙江大学 电气工程学院,浙江 杭州 310027;2.广东省粤电集团有限公司,广东 广州 510630)
0 引言
电力负荷预测,尤其是短期和超短期预测,是现代电力系统运行的基础,其预测精度对系统的安全经济运行具有重要影响[1]。其中,短期预测是对未来一日或几日每个采样点(每日等时间隔采样24,48或96次)用电负荷的预测,因此也称为日度预测[2]。超短期负荷预测是对当前时段往后一个或几个时间点(每个时间点间隔5,10,15或30 min)用电负荷的预测,因此也称为时分预测[2]。
为准确预测短期和超短期负荷,国内外很多学者做了大量研究工作,提出了回归分析法[3]、人工神经元网络法[4]、支持向量机法[5]、灰色模型法[6]等诸多方法。然而,这些方法都只能得到确定性的点预测结果,由于预测过程中存在的不确定因素,得到的预测结果一般都有不同程度的误差。
随着电力系统负荷特性趋于复杂,负荷预测难度随之增加,而另一方面电力系统运行对负荷预测结果的准确性的要求不断提高,传统的点预测方法越来越难以满足电力系统运行的实际需求。在此背景下,区间预测方法逐步受到重视。区间预测方法可以对由不确定性因素引起的预测结果变动范围进行量化,实际负荷观测值以一定期望概率落在区间上、下界确定的预测区间内,可用于电力系统短期和超短期负荷预测,得到合理的预测区间[7]。
现有的区间预测方法普遍存在计算复杂、假设性强、预测时间长等问题[8,9],因此有必要寻求更加简单高效的方法来构建预测区间。以电力系统短期和超短期负荷预测为应用背景,本文对区间预测技术进行了新的探索,以极限学习机点预测模型为基础,提出了比例系数法,并用实际数据说明了该方法的预测性能。
1 极限学习机理论与和声搜索算法
1.1 极限学习机理论
极限学习机(Extreme Learning Machine)是单隐含层前向神经网络的一种学习算法,网络结构如附录图1所示(略)。该算法只需设定隐含层节点数以确定网络结构,网络的输出权值能由随机产生的隐含层节点学习参数直接解析确定而无需迭代调整,网络训练速度极快。同时,该算法能保证在已有条件下网络训练误差最小且由解析获得的输出权值范数最小,因此具备比常规单隐含层神经网络更好的泛化能力[10]。
极限学习机算法的主要思想如下所述:
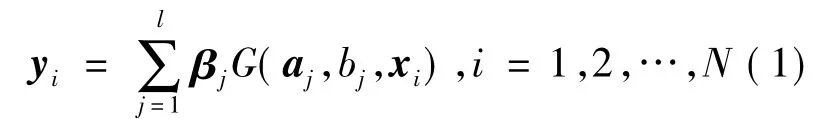
可以证明[12],如果隐含层节点个数l与训练样本个数N相等,则任取隐含层节点的学习参数(下文简称学习参数)aj∈ ℝn,bj∈ ℝ (j=1,2,…,l),该网络都能够以零误差逼近训练样本,即此时有:
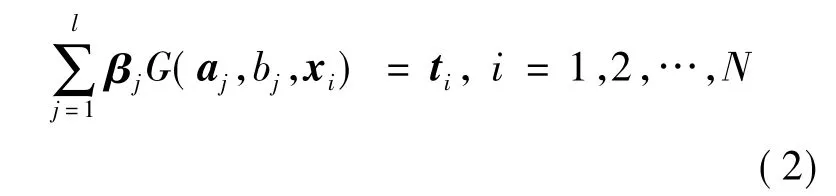
上述N个等式可以表示为如下矩阵形式:

式中:
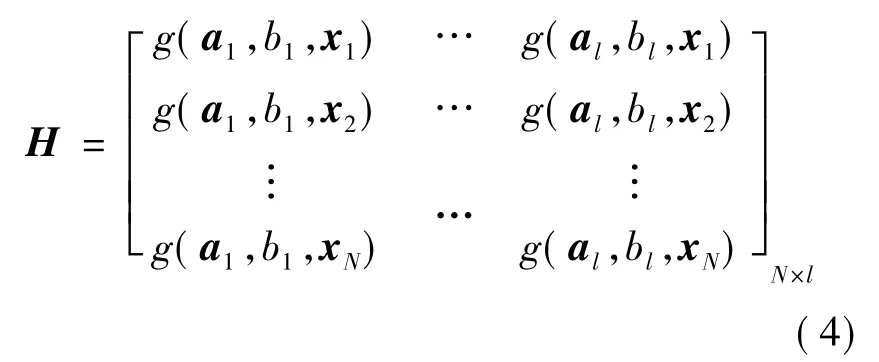

当训练集样本个数很大时,为了减少计算量,l通常取比N小的数,在这种情况下,极限学习机算法在训练前随机选择学习参数aj∈ℝn,bj∈ℝ (j=1,2,…,l)且在训练过程中保持不变。训练这个网络等同于求解以β为变量的线性系统Hβ =T 的最小二乘解[13],即
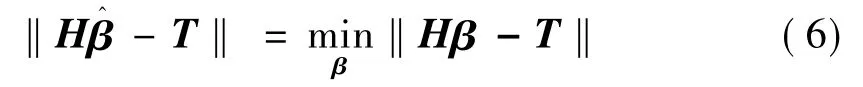
其解为

式中:H+为隐含层输出矩阵H的摩尔-彭洛斯(Moore-Penrose)广义逆矩阵,可以通过正交投影法或奇异值分解法等方法[14]解析获取。
1.2 和声搜索算法
和声搜索(Harmony Search)算法是一种新兴的具备全局搜索能力的智能优化算法[15]。这种算法模拟了乐队演奏时乐师们寻求美妙和声状态的过程,具有程序实现简单、求解速度快、寻优能力强等优点。对于一些工程优化问题,其算法性能比一些常规智能优化算法(如遗传算法和模拟退火方法法)更加有效[16,17]。
和声搜索算法包括下述特征参数:a.和声记忆库规模(Harmony Memory Size),SHM,即和声记忆库(Harmony Memory)能存放的解向量数目,和声记忆库在迭代过程中保持与外部信息交换更新,保证库内存放解向量的多样性和较优性;b.和声记忆库内取值率(Harmony Memory Considering Rate),RHM,其值决定迭代过程中和声记忆库内搜索解向量的概率,较高的RHM值将保证待搜索的解向量能充分继承库内较优解的相应信息;c.音调调节率(Pitch Adjusting Rate),PHM,和音调调节带宽bHM,通过适当设置PHM和bHM可使解向量跳出局部最优值,提高全局搜索能力;(4)创作次数 (Number of Improvisations),NHM,即算法的最大迭代次数,通常作为判定算法是否需要终止的条件参数。具体实现过程如下所述[18,19]:
STEP 1设置算法参数与初始化和声记忆库定义优化问题的目标函数f(·)、解向量维数DHM及变量取值范围,并设置算法的特征参数,即SHM,RHM,PHM,bHM和 NHM。之后,在和声记忆库里随机产生SHM个初始解z1,z2,…,zSHM并计算相应目标函数值f(z1),f(z2),…,f(zSHM)。
STEP 2生成新的解向量
STEP 3评估新生成的解向量
对STEP 2生成的解向量进行评估,即将zNEW对应的目标函数值f(zNew)与和声记忆库内已有解向量的最劣目标函数值f(zWorst)进行比较,如果优于f(zWorst),则将新生成的解向量存入记忆库并替换出f(zWorst)对应的解向量。
STEP 4判定是否满足终止条件
重复STEP 2和STEP 3,直至迭代次数i达到NHM。同时,为提高该算法的全局寻优能力和鲁棒性,在迭代过程中对RHM和PHM进行自适应取值,使得算法在迭代初期以较高概率搜索到相对较优解,并能在迭代后期扩大搜索范围,避免陷入局部最优解。自适应取值的数学表达式为[20]

2 预测区间评估指标
2.1 区间覆盖率
区间覆盖率 (Coverage Probability),χCP,是衡量预测区间质量的最关键指标,其定义了实际观测值(下文简称观测值)落在由上下界包络的预测区间内的概率。χCP值越大表示有越多的观测值被构建的预测区间所覆盖,反之亦然。在理想情况下,χCP=100%,此时所有的观测值都位于预测区间内。
通常,期望观测值以不低于额定置信水平的一定概率p落在所构建的预测区间内,即
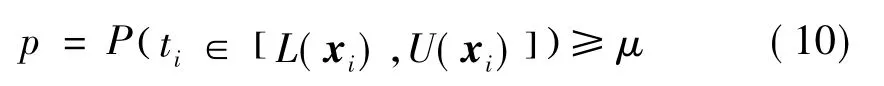
式中:P(·)表示概率;L(xi)和U(xi)分别是由xi预测得到的预测区间下界和上界;ti为与xi对应的观测值;μ为额定置信水平,其与显著性水平γ的关系为
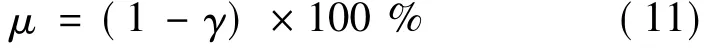
根据伯努利大数定律,可以直接用预测区间覆盖观测值的频率来表示χCP,其将依概率收敛于p,即
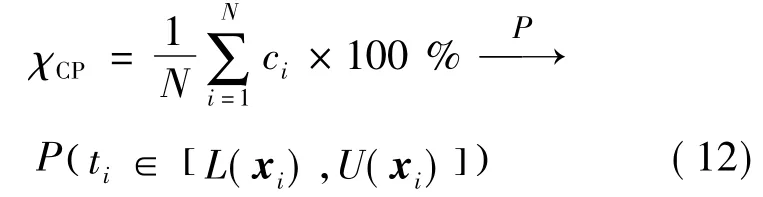
式中:N为预测样本的个数,ci为布尔量
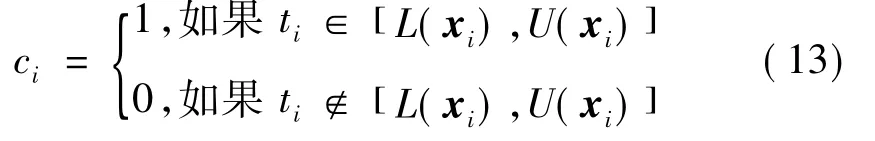
为构建有效的预测区间,χCP应高于额定置信水平μ;如果χCP远小于μ,则该预测区间视作无效区间,需重新构建。
2.2 平均宽度百分比
预测区间宽度是评估预测区间质量的重要参考依据。如果区间足够宽,则很容易满足χCP=100%的理想区间覆盖率,然而这样的区间过于保守,并不能给出关于待预测值不确定性的有效信息,使得区间预测的结果没有实用价值[21]。为了更合理地评价预测区间,还需要度量区间宽度。定义平均宽度百分比 (Mean Width Percentage)指标χMWP如式(14):

该指标度量了每个待预测点的预测区间宽度占观测值的平均百分比。需要指出,以相对宽度来度量预测区间往往比绝对宽度更具实用价值。在负荷预测问题中,用电高峰时的负荷往往难以准确预测,预测区间理应较宽,而用电低谷时的预测准确度相对较高,预测区间相对较窄,因此以绝对宽度评估高峰和低谷负荷预测区间并不能准确反映预测区间的优劣。预测区间宽度一般与观测值大小呈正相关,借助χMWP能对区间宽度做出更准确评价。在极端条件下,N个待预测点的预测区间上下界都相同,则预测区间宽度全都为零,此时区间预测退化为点预测,关于预测区间的评估指标就失去实际意义。本文严格区分点预测和区间预测,定义预测区间均需满足xMWP≠0。
2.3 累积偏差
已有关于区间预测的研究普遍采用了χCP和类似 χMWP的指标[9,21~27],但仅靠这两个指标并不能完全评估所构建预测区间的优劣。以图1为例对此进行说明。子图(a)和(b)为对同一待测数据集构建预测区间的两种不同情况,可以看出两个区间的χCP和χMWP的值均相同,但未被预测区间覆盖的两个真实数据偏离预测区间上界(或下界)的程度不同,子图(a)中两点的偏离程度明显大于图(b)中两点,故一般认为子图(b)的预测区间要优于子图(a)。然而,现有的评估指标体系并不能将这两个区间的优劣做出评判,往往将两个区间视为等效区间。这里引入一个新指标,即累积偏差(Accumulated Deviation),χAD,计算式为
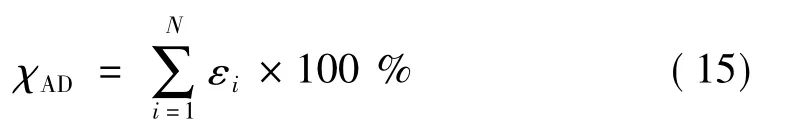
式中:εi表示观测值偏离预测区间上界(或下界)的程度,表示为

与χMWP类似,也采用相对偏离程度来确定χAD。在相同χCP和χMWP的条件下,χAD越小则预测区间质量一般越高。
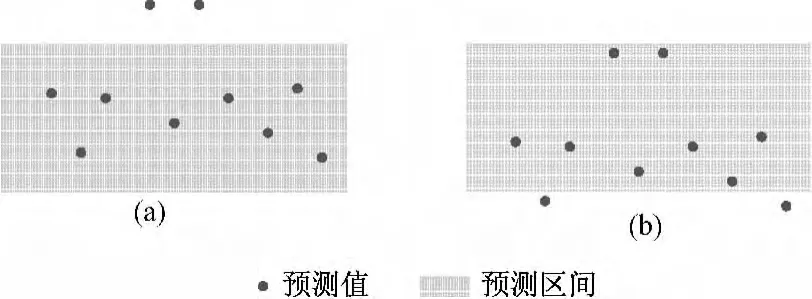
图1 两类预测区间比较示意图Fig.1 Comparison between two kinds of prediction intervals
2.4 预测区间满意度
χCP,χMWP和χAD3个指标相互独立,都只考虑了预测区间的某一性质,依据任何一个或两个指标都不能对预测区间做出完全而准确的评估。理想的预测区间需要在满足置信水平符合要求(χCP尽量大)的同时,区间宽度和未覆盖点偏离程度尽量小(即 χMWP和 χAD尽量小)。然而,由 χCP,χMWP和χAD的定义可知,这3个指标实际上是相互冲突的:χCP越大,往往 χMWP越大;χMWP越小,往往χCP越小而χAD越大;χAD越小,往往χMWP越大。因此,需要综合考虑这3个指标。这里提出能对预测区间进行量化评估的综合指标,即预测区间满意度指标 (Prediction Interval Satisfaction Index),χPISI,计算公式为
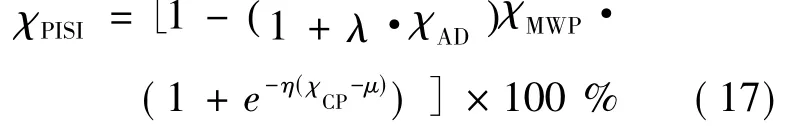
式中:λ,η和μ为χPISI的3个控制参数,可以根据实际需要设定;λ和η分别为对χAD和χCP的惩罚系数,μ为给定的置信水平。
如前所述,χCP是评判预测区间优劣的最关键指标,一般而言在χCP不低于μ的情况下评估预测区间才有意义。实际上,χCP由有限样本统计得到,其值可能会稍小于μ,此时同样可以对相应预测区间进行评估[25]。附录图2(略)描绘了χPISI关于 χCP的函数 (1+e-η·(χCP-μ)) 随 χCP不同取值的变化规律(图中 η =50,μ =90%)。当 χCP高于 μ时,该函数走势平缓并渐近趋于1,此时χPISI主要受χMWP和χAD影响;而当χCP低于μ时,函数值随着χCP偏离μ而陡增,此时χCP对χPISI的计算起主导作用。
χPISI综合考虑并有效结合了 χCP,χMWP和 χAD这3个指标,可以作为评判预测区间优劣的指标。为使χPISI更具实际意义,这里定义:当χPISI的计算结果小于0时,χPISI值取0。因此,χPISI始终在[0,100%)范围内取值,χPISI值越大,可认为预测区间质量越高。当χCP等于100%,χAD等于0%;当χMWP值趋近0%时,χPISI值趋近100%。对于χPISI值只能无限趋近而不能达到100%这一现象,可以解释为在实际预测过程中更希望得到的预测结果是确定的准确值,而非可能出现的某个变动区间,用“不确定”的区间预测代替“确定”的点预测只是对某些不确定因素的“妥协”,因此区间预测的结果永远不是最满意(对应χPISI=100%)的。
3 比例系数法主要思想
3.1 预测值与预测区间
基于神经网络的 Bootstrap法[28]是目前应用最广泛的区间预测方法[21],其假设对预测模型集成后得到的点预测值(下文简称预测值)能以很小偏差(甚至无偏)估计真实回归值(下文简称真实值),即观测值的期望值,继而以预测值为中心构建对称的预测区间,保证观测值以不低于额定置信水平的概率落在此区间内。此种假设下,预测值和预测区间如图2(a)所示,预测值能以很小的偏差逼近真实值(甚至与真实值重合),构建的预测区间近似于以真实值为中心对称分布。
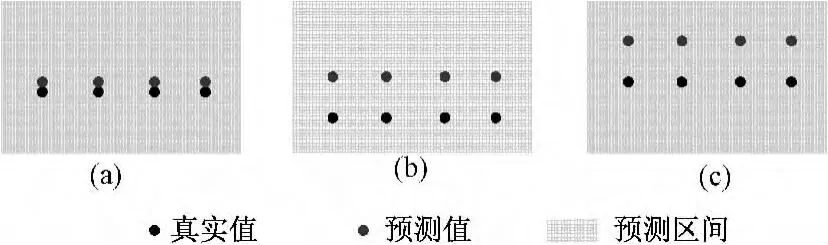
图2 点预测值与预测区间示意图Fig.2 Prediction point and prediction interval
理论上可以证明[29],以真实值为中心对称的预测区间要较不对称的预测区间更优。实际上,真实值难以获取,而由于数据噪声及预测模型本身不确定性的影响,预测值很多情况下并不能作为真实值的无偏估计值。以极限学习机对短期(或超短期)负荷进行点预测为例,对此进行说明。一方面,在预测过程中选用的历史负荷数据从SCADA系统获取,而由于SCADA系统采集过程中的一些偏差会使所采集的负荷观测值偏离真实值[1],因此极限学习机的输入量和期望输出量都能视为被数据噪声污染的随机变量,使得预测结果可信度降低。另一方面,极限学习机模型本身会对预测精度造成影响。预测过程中,往往难以确定最优的特征输入量、学习参数和网络结构,而根据经验选取的特征输入量和隐含层节点数及随机选取的学习参数使得模型预测性能达不到要求。即使极限学习机能零偏差学习训练样本,然而由于样本数据有限,难以保证模型对所有待预测样本均能适用,而且训练样本中往往存在“尖峰”数据,为平缓这些“尖峰”,极限学习机的输出值都会有偏离真实值趋向,导致预测精度达不到要求。如果由预测值估计真实值有较大偏差,此时以预测值为对称中心构建的预测区间很难满足要求,如图2(b)。
通过对数据进行预处理(如替换异常值、非线性去噪等[30])和提高模型的预测精度和泛化能力[31],能使得预测值以更小的误差估计真实值。然而,这些处理手段都需要靠经验选取或经过反复试错后找到,实际预测过程中往往难以将其全部实现。当预测值估计真实值的偏差不能忽略时,但是依然可以通过构建如图2(c)中的预测区间来抵消此偏差,此时区间并不再以预测值为中心对称。
3.2 比例系数法
本文提出的方法将极限学习机(网络模型如附录图3(略))对预测样本(或称预测集)的输出值分别放大和缩小比例系数α和β得到的结果作为预测区间的上界和下界,故称其为比例系数法。数学表达式为
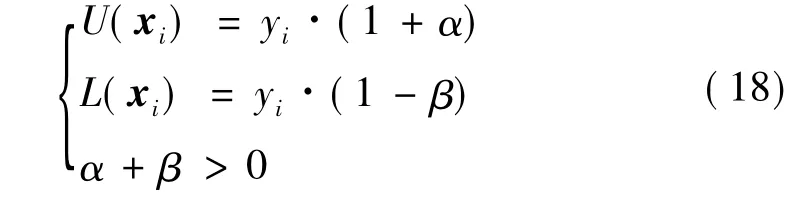
式中:yi是极限学习机输入量为xi的输出值;U(xi)和L(xi)为对应xi构建的预测区间上界和下界;α和β为需要确定的两个比例系数。
为获得α和β并保证其能确定最优的预测区间,假设比例系数在连续时间段内的变化态势是平滑的,α和β则近似于对近期历史数据进行事后预测并评估后确定的最优比例系数和(对应的事后预测区间最优)。因此,α和β可以由式(19)确定:

基于以上思想,比例系数法将近期历史数据构成的另一个预测样本(称为验证集),根据同一极限学习机的对应输出值类似式(18)构建验证集预测区间,并用验证集观测值对预测区间进行评估,比例系数αValid和βValid在指定范围内不断调整,直至获得χPISI值最高的预测区间,即求解如下优化问题:
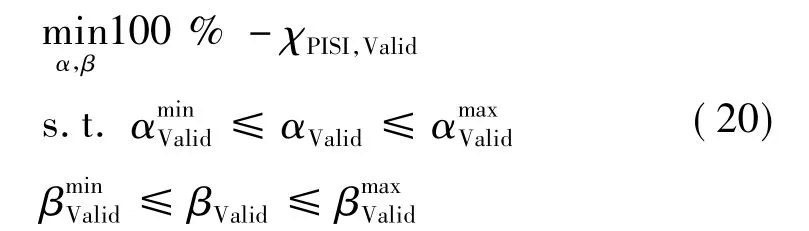
式中: χPISI,Valid为验证集的 χPISI值,和分别为验证集比例系数αValid和βValid的指定最小值、最大值。
考虑到价值函数即“100% - χPISI,Valid”的函数形态复杂性,本文采用和声搜索算法对αValid和βValid进行寻优,最小价值函数对应的和即为需要确定的比例系数,根据式(18)对预测集构建预测区间。
由于通过集成可以增加预测模型的稳定性并且提高预测精度,比例系数法也引入了集成技术。这里首先给出两个不同思路:
(1)将M个极限学习机对应验证集和预测集的输出值取中位值,以期望获得更精确的预测值y*(xi),即
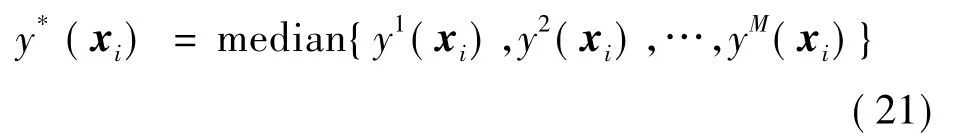
式中:median{·}表示取中位数。
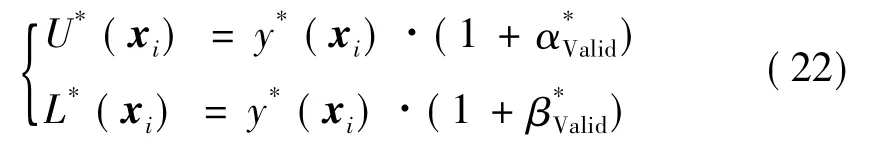
(2)验证集根据要集成的第k个极限学习机对应输出值确定一组比例系数和,随后预测集根据同个极限学习机对应输出值yk(xi)构建一组区间上下界Uk(xi)和Lk(xi),即
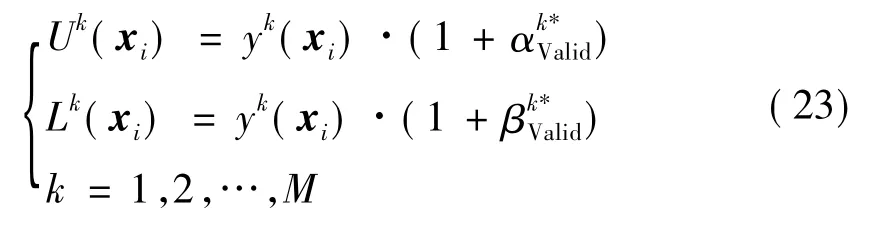
最后对所得的M个区间进行集成,分别取区间上、下界的中位值作为最终预测区间上、下界U*(xi)和L*(xi),即
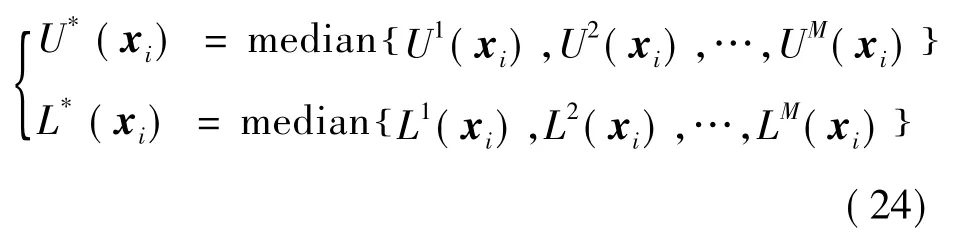
以上两种思路均能反映比例系数法的主要思想,由于比例系数法本质上不严格区分预测值偏离真实值的程度,而每组预测值均能对应一个高质量的预测区间(如图2(a)和图2(c)),从统计角度而言,思路(2)能以更高概率找到最优区间,因此本文采用的是思路(2)的方案。
此外,由于极限学习机网络结构取决于隐含层节点个数,如果节点过少,则会导致模型学习能力有限,影响预测结果的精度,如果节点过多,则容易导致“过拟合”,影响模型的泛化能力。同时,由于极限学习机随机选取隐含层节点学习参数,不同的参数将对应不同的最优网络结构,即其最优隐含层节点数不是一个固定值,而是在某个区间变动。因此,比例系数法集成的极限学习机,在指定区间内选取隐含层节点数,以增加网络结构的多样性使集成的结果更稳定[32]。
附录图4(略)给出了使用比例系数法对负荷进行区间预测的实现流程,具体步骤如下所述:
STEP 1选取特征输入量,构造训练集和验证集
选取历史负荷数据划分训练集和验证集,并根据训练集负荷数据特性确定极限学习机特征输入量 xi=[xi1,xi2,…,xin]T∈ ℝn。
STEP 2确定隐含层节点数最优选取区间
选取不同隐含层节点数的极限学习机学习训练集数据,随后对验证集进行区间预测,根据χPISI对所得预测区间进行评估,确定隐含层节点最优选择区间(下文简称选择区间)。
STEP 3训练极限学习机,对验证集和预测集进行点预测
从选择区间随机选取隐含层节点数并从指定范围内选取相应网络结构的学习参数,使用训练集数据对极限学习机进行训练。使用训练过的极限学习机对验证集和预测集分别进行点预测。
STEP 4确定比例系数
使用和声搜索算法在给定范围内寻找能使验证集χPISI最大的α和β,根据寻优得到的最优比例系数计算预测集的预测区间上下界,并将此结果保存。
STEP 5判定是否完成集成
判定集成的极限学习机个数是否已达到给定集成数M,如果没有达到M,则重复STEP 3和STEP 4。
STEP 6确定预测集预测区间
取预测集在集成过程中得到的M个上、下界结果的中位值,分别作为所要构建预测区间的上、下界。
4 算例分析
为验证比例系数法应用于负荷预测的正确性和有效性,本文选取2007年度浙江某城市冬季和夏季的两个典型月(即1月和7月)实际用电负荷数据为样本,分别进行短期预测和超短期预测研究。其中,短期预测的对象是次日全天96点负荷观测值(从0:00至23:45每隔15 min进行一次采样,共计96个采样点),超短期预测则对下一采样点(时间间隔为15 min)的负荷观测值进行在线预测。由于高比重的取暖(或空调)负荷以及节假日的影响,这两个月的用电负荷并无明显的变化规律(如日类型)可遵循,常规的点预测方法很难满足实际需求,因此对其进行区间预测更为合理。
4.1 数据样本集和特征输入量
将1月和7月由日96点负荷数据组成的样本集根据时间先后顺序分别以70% ~20% ~10%的比例划分为3个互不重叠的样本子集:训练集、验证集和预测集,划分结果见附录表1(略)。此外,本文研究过程中以日为窗口单元对训练集和验证集进行滚动更新,如附录图5(略)。
由于选取合适的特征输入量能提高极限学习机的预测精度,而这2个月负荷特性较为复杂,很难根据经验选取合适的特征输入量,因此借助于ARIMA(Autoregressive Integrated Moving Average model)中的偏自相关函数来帮助选取特征输入量。对训练集历史负荷数据构成的时间序列进行偏自相关分析,选取偏自相关系数最大的5个“已知”负荷数据作为特征输入量 xi1,xi2,xi3,xi4和xi5。选取结果见附录表2(略)。由于负荷数值落在神经元的有效区间外将引起神经元的饱和,需要将所有负荷数据归一化到区间[-1,1],并对最终预测结果进行相应的反归一化。
为增强极限学习机的学习能力,使之辨识不同时刻的负荷值,增加与各采样点时标相关的特征输入量xi6,xi7,并按如下规则进行编码:
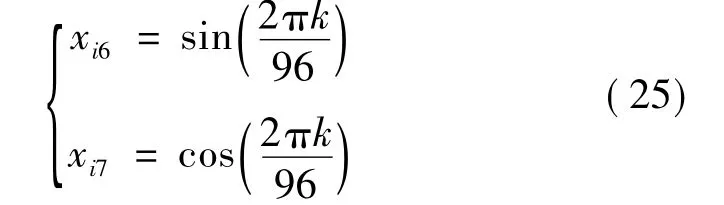
式中:k为与各采样点对应的时标(k=1,2,…,96)。
在此编码规则下,各采样点的时标能由xi6和xi7联合确定,且由于xi6和xi7均在区间[-1,1]内取值,所以无需再对其进行归一化。
4.2 模型参数
极限学习机隐含层节点选为加法型节点,激活函数为Sigmoid函数,输入权值和阈值均从[-1,1]范围内随机选取。附录表3(略)和附录表4(略)分别给出了和声搜索算法和χPISI的特征参数值以及隐含层节点数和比例系数的选择区间。附录图6(略)描绘了对1月负荷进行超短期预测时,验证集价值函数值在和声搜索过程中的典型演变情况。
4.3 结果分析与比较
将比例系数法与文献[33]总结的配对自助法(Pairs Bootstrap)进行比较,其中配对自助法实验过程中不区分训练集和验证集,集成数均取100。为消除算法的随机性,重复实验10次,预测区间按日进行划分并用实际观测值对当日预测区间进行评估,将所得χPISI的中位值对应的预测区间取为最终结果。表1和表2分别比较了比例系数法和配对自助法的超短期和短期区间预测结果。图3和图4给出了比例系数法对1月负荷进行超短期和短期区间预测的结果,7月的相应结果请见附录图7(略)和附录图8(略)。配对自助法的短期区间预测结果如附录图9(略)和附录图10(略)所示。
(1)超短期预测结果及分析
从表1中容易看出,比例系数法确定的预测区间的χPISI基本都要高于配对自助法,且χPISI能基本稳定在一个较高水平(1月为94%,7月为96%),而后者的χPISI波动较大(1月波动幅度约10%,7月波动幅度约3%)。比例系数法构建预测区间过程中,和声搜索算法寻优得到的比例系数结果典型值为:1月=0.0224,=0.0265,7 月=0.0183,=0.0175,可以推知,预测值可以作为真实值的近似无偏估计值,使得预测区间近似以预测值为中心对称。此时,使用配对自助法同样可以获得较为满意的结果。
(2)短期预测结果及分析
从表2中数据容易得知,比例系数法确定的预测区间的χPISI要远比配对自助法稳定,后者甚至出现了χPISI=0的情况。比例系数法构建预测区间过程中,和声搜索算法寻优得到的比例系数结果典型值为:1月= 0.0433,=0.0825,7月=0.1108,=0.0595,此时预测区间不再以预测值为中心对称,由预测值估计真实值将导致较大偏差。因此,基于预测值能够无偏估计真实值的假设的配对自助法并不能给出可信的预测区间。此时,配对自助法确定的1月和7月的预测区间由于预测值估计真实值时分别上偏和下偏,导致获得的预测区间也相应上偏和下偏,均不能很好的覆盖全部观测值,而比例系数法通过控制αValid和βValid的取值,通过构建不对称的预测区间,对预测值估计真实值的偏差进行了修正,依然可以获得较为满意的结果。
与超短期预测结果类似,短期预测时虽然比例系数法确定的区间χMWP要高于配对自助法,但前者往往能够获得更高的χCP和χAD,使得χPISI也更高,因此前者构建的预测区间质量也往往更高。此外,短期预测时,预测区间χMWP明显大于超短期预测时的对应值,这一现象符合区间预测的特征,即不确定性越大,预测区间结果将越保守,此时预测区间也就越宽。本文研究中为更好地反映负荷预测的不确定性,在短期预测时,并未计入气象因素的影响。在条件允许的情况下,增加相关的气象因素(主要是温度)为特征输入量将有助于提高预测准确度,进而降低预测区间的χMWP。
如果实际生产运行过程中需要待预测日的确定性点预测值,则可以将由预测区间上下界确定的区间中值作为点预测值,即
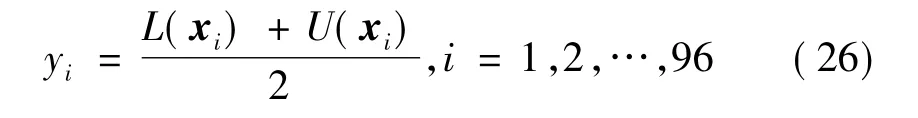
式中:yi和xi分别为待预测日第i个时刻的点预测值和极限学习机输入量;L(xi)和U(xi)为与xi对应的预测区间下界和上界。
对由比例系数法和配对自助法得到的预测区间分别由式(26)确定点预测值,并根据文献[34]提供的评价点预测结果的日负荷预测准确率A的计算公式进行评估:
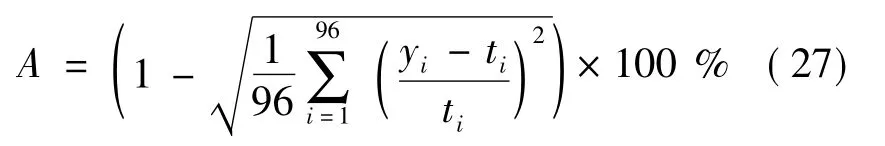
表3对两个方法确定的点预测结果进行了比较。比例系数法确定的点预测值在多数情况下比配对自助法的结果准确率更高,而后者得到的点预测值本质上是对集成的多个极限学习机输出值取平均值后的结果。可以推知,负荷预测的不确定性较大时,依然可以通过由比例系数法构造的预测区间中值来获得较高准确率的点预测值。
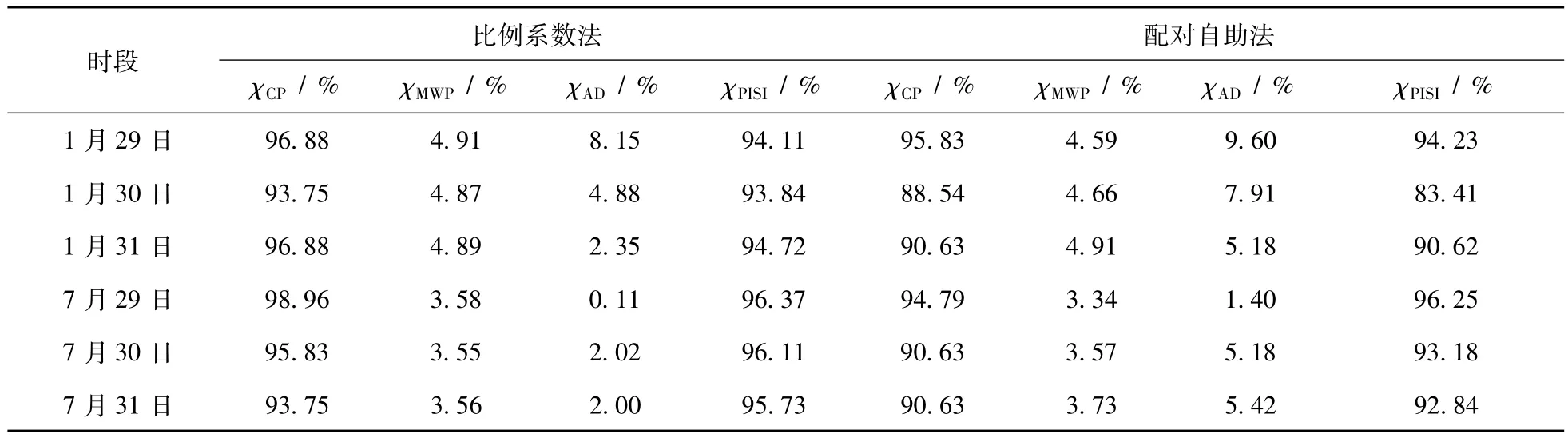
表1 超短期负荷区间预测结果Tab.1 Results of ultra-short-term load interval prediction
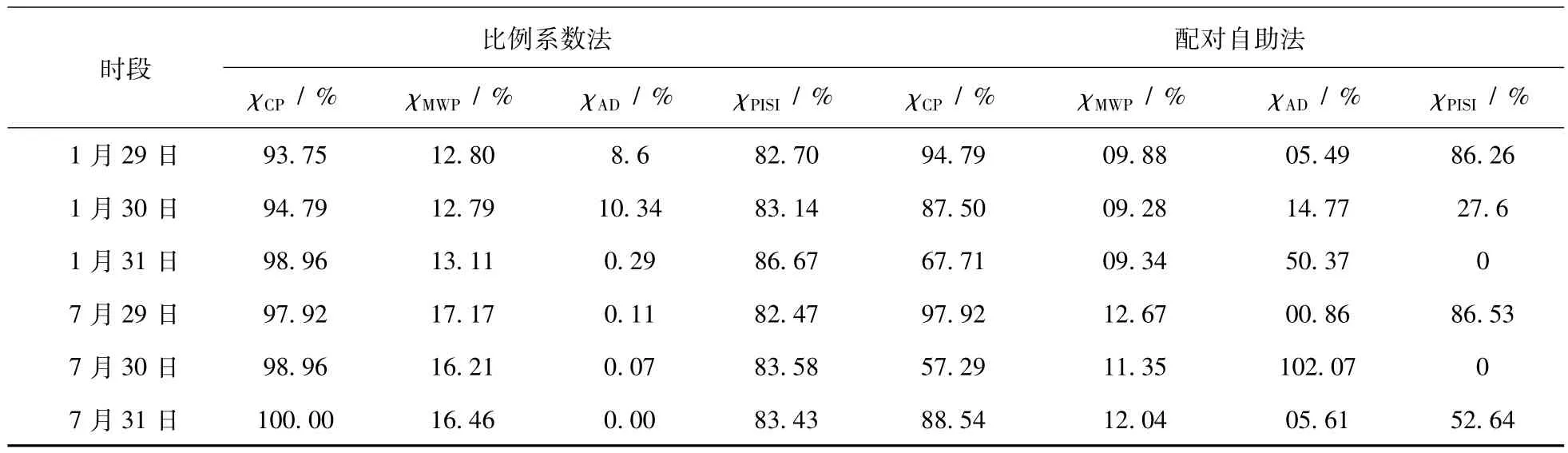
表2 短期负荷区间预测结果对比Tab.2 Results of short-term load interval prediction
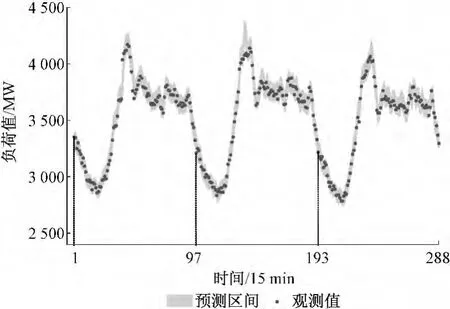
图3 超短期负荷区间预测结果(1月)Fig.3 Results of ultra-short-term load interval prediction in January
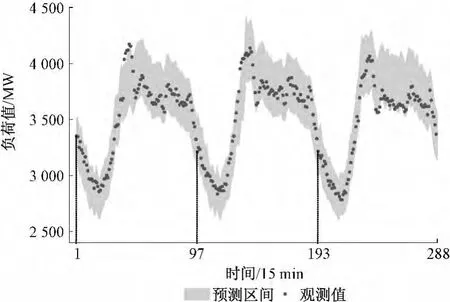
图4 短期负荷区间预测结果(1月)Fig.4 Results of short-term load interval prediction in January

表3 日负荷预测准确率Tab.3 Daily load forecasting accuracy
5 结论
负荷区间预测的结果,可以使电力系统决策人员更好地认识到未来负荷的不确定性及相关的风险信息,使其及时做出更加合理的决策[35]。本文提出的比例系数法简单高效,适用范围广,能够构建高质量的预测区间。当预测值能近似无偏估计真实值时,构建的预测区间近似以预测值为中心对称且区间宽度小。当由预测值估计真实值存在较大偏差时,预测区间则不再对称且区间宽度大。最后需要指出,比例系数法的主要思想并不局限于超短期和短期负荷预测,在其他领域(如风电和水文预测)同样具有很好的应用前景。
(因篇幅所限附录略,如读者需要可与作者联系)
[1]何洋,邹波,李文启,等.基于混沌理论的电力系统短期负荷预测的局域模型[J].华北电力大学学报 (自然科学版),2013,40(4):43-50.
[2]郑金.短期电力负荷预测方法研究[D].郑州:郑州大学,2012.
[3]汪峰,于尔铿,阎承山,等.基于因素影响的电力系统短期负荷预报方法的研究[J].中国电机工程学报,1999,19(8):54-58.
[4]周佃民,管晓宏,孙 婕,等.基于神经网络的电力系统短期负荷预测研究[J].电网技术,2002,26(2):10-13.
[5]李元诚,方廷健,于尔铿.短期负荷预测的支持向量机方法研究[J].中国电机工程学报,2003,23(6):55-59.
[6]焦润海,苏辰隽,林碧英,等.基于气象信息因素修正的灰色短期负荷预测模型[J].电网技术,2013,37(3):720-725.
[7]林晓华,冯毅雄,谭建荣.基于免疫优化的产品系统可靠性参数区间预测方法[J].浙江大学学报(工学版),2013,(6):1013-1021.
[8]杜雅楠.基于核学习的冶金煤气流量在线区间预测方法[D].大连:大连理工大学,2013.
[9]Quan H,Srinivasan D,Khosravi A.Short-term load and wind power forecasting using neural network-based prediction intervals[J].IEEE Transactions on Neural Networks and Learning Systems,2013,25(2):303-315.
[10]Huang G,Zhu Q,Siew C.Extreme learning machine:theory and applications[J].Neurocomputing,2006,70(1):489-501.
[11]Lan Y,Soh Y C,Huang G.Ensemble of online sequential extreme learning machine[J].Neurocomputing,2009,72(13):3391-3395.
[12]Liang N,Huang G,Saratchandran P,et al.A fast and accurate online sequential learning algorithm for feedforward networks[J].IEEE Transactions on Neural Networks,2006,17(6):1411 -1423.
[13]高光勇,蒋国平.采用优化极限学习机的多变量混沌时间序列预测[J].物理学报,2012,61(4):37-45.
[14]Zhao J,Wang Z,Park D S.Online sequential extreme learning machine with forgetting mechanism[J].Neurocomputing,2012,87(11):79-89.
[15]Geem Z W,Kim J H,Loganathan G V.A new heuristic optimization algorithm:harmony search[J].Simulation,2001,76(2):60-68.
[16]Lee K S,Geem Z W.A new meta-heuristic algorithm for continuous engineering optimization:harmony search theory and practice[J].Computer Methods in Applied Mechanics and Engineering,2005,194(36 - 38):3902-3933.
[17]Geem Z W.Optimal cost design of water distribution networks using harmony search[J].Engineering Optimization,2006,38(3):259-280.
[18]雍龙泉.和声搜索算法研究进展[J].计算机系统应用,2011,20(7):244-248.
[19]刘蓓,汪沨,陈春,等.和声算法在含DG配电网故障定位中的应用[J].电工技术学报,2013,28(5):280-284.
[20]刘思远,柳景青.一种新的多目标改进和声搜索优化算法[J].计算机工程与应用,2010,46(34):27-30.
[21]Khosravi A,Nahavandi S,Creighton D,et al.Comprehensive review of neural network-based prediction intervals and new advances[J].IEEE Transactions on Neural Networks,2011,22(9):1341-1356.
[22]Quan H,Srinivasan D,Khosravi A.Construction of neural network-based prediction intervals using particle swarm optimization[C].The 2012 International Joint Conference on Neural Networks(IJCNN),New York:IEEE,2012.
[23]Khosravi A,Nahavandi S.Combined nonparametric prediction intervals for wind power generation[J].IEEE Transactions on Sustainable Energy,2013,4(4):849-856.
[24]Khosravi A,Nahavandi S,Creighton D.A neural net-work-GARCH-based method for construction of prediction intervals[J].Electric Power Systems Research,2013,96(3):185-193.
[25]Khosravi A,Nahavandi S,Creighton D.Construction of optimal prediction intervals for load forecasting problems[J].IEEE Transactions on Power Systems,2010,25(3):1496-1503.
[26]Khosravi A,Nahavandi S,Creighton D.Prediction intervals for short-term wind farm power generation forecasts[J].IEEE Transactions on Sustainable Energy,2013,4(3):602-610.
[27]Khosravi A,Nahavandi S,Creighton D,et al.Lower upper bound estimation method for construction of neural network-based prediction intervals[J].IEEE Transactions on Neural Networks,2011,22(3):337-346.
[28]Efron B.1977 Rietz lecture-bootstrap methods:another look at the jackknife[J].The Annals of Statistics,1979,7(1):1-26.
[29]魏宗舒.概率论与数理统计教程[M].高等教育出版社,2008.
[30]Harrison R G,Yu D J,Oxley L,et al.Non-linear noise reduction and detecting chaos:some evidence from the S&P composite price index[J].Mathematics and Computers in Simulation,1999,48(4):497 -502.
[31]毛力,王运涛,刘兴阳,等.基于改进极限学习机的短期电力负荷预测方法[J].电力系统保护与控制,2012,40(20):140-144.
[32]Zhang R,Dong Z Y,Xu Y,et al.Short-term load forecasting of Australian national electricity market by an ensemble model of extreme learning machine[J].IET Generation,Transmission & Distribution,2013,7(4):391-397.
[33]Wan C,Xu Z,Pinson P,et al.Probabilistic forecasting of wind power generation using extreme learning machine[J].IEEE Transactions on Power Systems,2013,PP(99):1-12.
[34]陈亚红,马丽,穆钢,等.两种短期负荷预测精度考核标准的比较[J].电力系统自动化.2003,27(17):73-77.
[35]方仍存.电力系统负荷区间预测[D].武汉:华中科技大学,2008.

