热力管网模型及单点泄漏故障诊断方法研究

吕玉坤，程 博，赵 锴，彭 鑫，李 聪

(1．华北电力大学 能源与动力工程学院，河北 保定 071003;2．杭州和利时自动化有限公司，陕西 西安 710075;3．华能荆门热电有限责任公司，湖北 荆门 448002)

0 引言

近年来，随着计算机技术、信息技术、空间技术以及人工智能技术等的不断发展[1，2]，热力管网故障诊断方法研究工作取得了突破性的进步。就总体而言，基于硬件的故障诊断技术虽然灵敏性好、定位准确，但由于其成本和施工费用高、实际管网发生泄漏情况无法预知，而且无法实时监测每个测点，故该类技术一般不作为热力管网故障诊断的主要手段[3，4];而基于软件的故障诊断技术其主要优点在于:可实时在线实现故障诊断、及时给出报警信号。因此，开展以软件为主、软硬件相结合的热力管网故障诊断方法的研究工作，以实现优势互补、提高热力管网管理的自动化水平，从而保证管网安全生产和经济运行已成必然之势。

笔者以国际上公认的管道泄漏检测与定位系统的9项性能指标为依据，对各种故障诊断方法进行综合比较后发现:基于状态估计的实时模型法[5，6]具有可很好地解决管道内流体特性参数随时间变化的特点，但其对流量计的要求高、误报警率高，且仅适用于小泄漏的管网故障诊断。有鉴于此，本文提出了适用于枝状热力管网单点泄漏的故障诊断方法——插入虚拟节点法。

插入虚拟节点法的基本思想是:假设管网某点泄漏后通过补水能够维持水压图达到新的平衡，把泄漏点视为一个新的热用户，即将泄漏点看作新插入的虚拟输出节点，则整个管网将仍满足流量守恒方程。

为实现实时在线故障诊断，与插入虚拟节点法相应地定义了一个管网报警阀的概念。以某市南市区的枝状热力管网从某正常运行状态过渡到故障状态为研究对象，采用图论和线性代数相结合的方法建立其热力管网水力计算模型，并应用环方程法求解之，以验证所提方法和所设管网报警阀值域的合理性。

1 热力管网水力模型与求解

图1为某市南市区的枝状热力管网图。供热总面积为1210.38万m2，单一热源厂供热，热源厂出口压力为0.5 MPa，供回水温度分别为120℃和60℃，水的平均密度取983.3 kg/m3，管材为无缝钢管，绝对粗糙度Δ=0.01 mm，供暖期为142天。

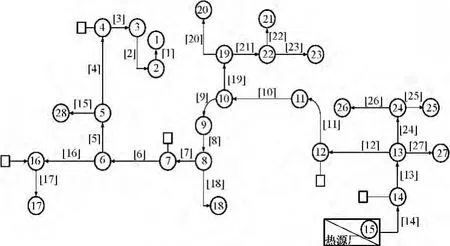
图1 某市南市区的枝状热力管网图Fig．1 Nanshi district of branched heat pipe network diagram

通过将实际热力管网简化和抽象为管线和节点两类组成元素，体现出它们之间的水力特性和拓扑关系，以便于图形、数据的表达和分析，为后续的水力计算、工况分析和故障诊断等工作奠定基础。热力管网数学模型本质上就是由管线和节点组成的一个有序的集合体。因此，可采用图论和线性代数相结合的方法，系统地建立其热力管网数学模型并求解之[7]。

1.1 热力管网水力模型的建立

根据实际工程的要求，为便于进行管网网络方程的建立，做出以下5个假设:

(1)管网中工质的流动为不可压缩流动;

(2)准稳态，热力管网特性参数(流量、压力等)不随时间变化;

(3)流动处于阻力平方区，ΔH=Sq2;

(4)动压忽略不计;

(5)热力管网的管线数为M、节点数为N，已知压力节点数为m。

基于管网水力计算基本方程的理论，应用图论理论和线性代数的思想建立管线与节点间的关系式。热力管网稳态运行时，均满足节点流量方程、管线能量方程、压降方程以及环方程[8]。

(1)节点流量方程。根据质量守恒定律可得:

将N个节点流量连续性方程相加可得到节点流量守恒方程式:

(2)管线能量方程。根据能量守恒定律可得:

(3)压降方程。考虑管线上加压泵的设置和水平位置的变化等情况，管线压降方程的表达式为

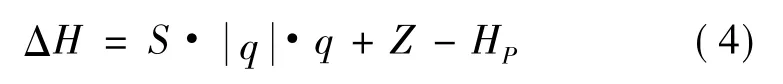
若不考虑上述因素影响，由假设(3)可知，对任意管线的管线压降公式可表示为

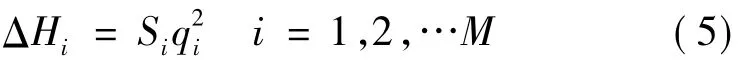
式中:Si为管线的阻抗系数，取决于管材、管长和管径。

(4)环方程。环方程的物理意义是指每个闭合回路中各管道的压力损失总和为零，也称回路方程;表达式为

由于热力管网供、回水管一般对称布置，且同一位置的供、回水管的管径、流量和阻力均相等。为了便于编程和计算，将热力管网的供、回水管分离，建模时只考虑供水管或回水管的水力特性，对于已知的热源输出流量和热力站设计流量均当作节点流量处理。

根据热力管网水力计算的基本方程，对于一个管线数为M、节点数为N的热力管网，可建立热力管网的通用数学模型如式(7):

式(1―7)中:A为N×M阶关联矩阵，表示管线和节点间的拓扑关系;AT为管网关联矩阵A的转置矩阵;A0为管网A的降阶关联矩阵，为(N－m)×M 阶矩阵;q 为管线流量向量，q=(q1，q2，…qM)T;Q 为 节 点 流 量 向 量，Q = (Q1，Q2，…QN-m)T;H 为 节 点 压 力 向 量，H =(H1，H2，…HN)T;ΔH为管段压力损失或压降向量，ΔH=(ΔH1，ΔH2，…ΔHM)T;S 为 N 阶对角阻力系数矩阵，S=diag(S1，S2，…SM);Z为管线上两节点的势能差向量，Z=(Z1，Z2，… ZM)T;Hp为管线中加压泵的扬程向量，Hp=(Hp1，Hp2，… HpM)T;B 为(M－R)×M阶基本回路矩阵，R为关联矩阵的秩。

1.2 热力管网水力模型的求解

当已知管径时，热力管网模型的方程组含有2M个未知数，可列出的方程数为

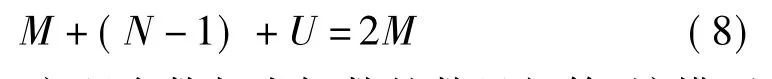
因此，方程个数与未知数的数目相等，该模型可以求解。但是，由于非线性方程组直接求解困难，本文中采用环方程法求解热力管网模型。

环方程法的基本思想是在满足节点流量方程的条件下，构造各环的能量方程组，通过求解各环校正流量的方法间接求出各管线流量，即Hardy Cross法，采用的环方程法需先拟定各管段流量初值[9]。

一般热力管网最初的设计流量难以满足环能量方程，因而第i环的环能量方程可表示为

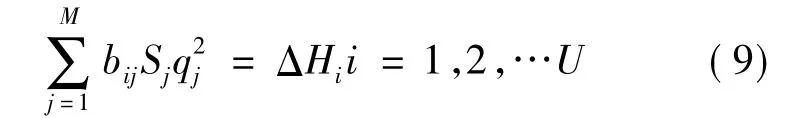
式中:ΔHi为第i环的压降闭合差。

为了满足各环压降闭合差的允许精度和节点流量方程的要求，引入第i环校正流量δqi，此时第i环的环能量方程为

式中:δqi的正负号与 bij一致;δqk为第 i环第 j管段邻环校正流量，正负号与bij相反。

采用麦克劳林级数展开(10)式，忽略 δqi，δqk二阶多项式，简化后表达式为

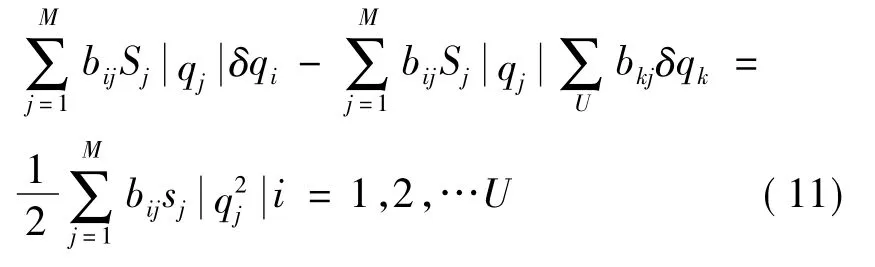
由式(11)构造环能量方程组，采用高斯－赛德尔法求解关于δHi的线性方程组，其方程组表达式为

[B·Λ·BT]·δq=1/2·B·Λ·q(12)式中:Λ为管线特性的对角矩阵，Λ=diag(S1|q1|，S2|q2|，…SM|qM|);δq 为管网环的校正流量，δq=(δq1，δq2，… δqU)T。其求解步骤如图2 所示。

2 报警阀 ε0和 εF定义

为实现实时在线故障诊断、定位热力管网泄漏点、减少管网诊断系统误报率[10]，需设置管线报警阀ε0和泄漏点报警阀εF。

2.1 管线报警阀ε0定义

热力管网正常运行时，假设管线i两端的节点压力为 Hi，Hi+1，则

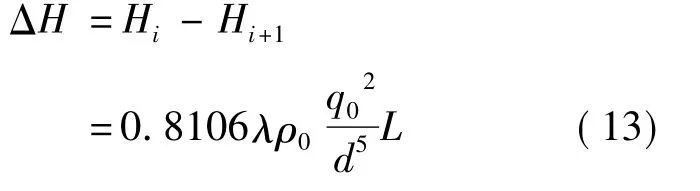
假设泄漏发生在管线i上，则其两端节点压力将变为H'i，H'i+1，泄漏量为QF，若将泄漏点视为插入输出节点，此时管线i仍将满足压降方程，即

泄漏前后，管线i两端的节点压力差值为

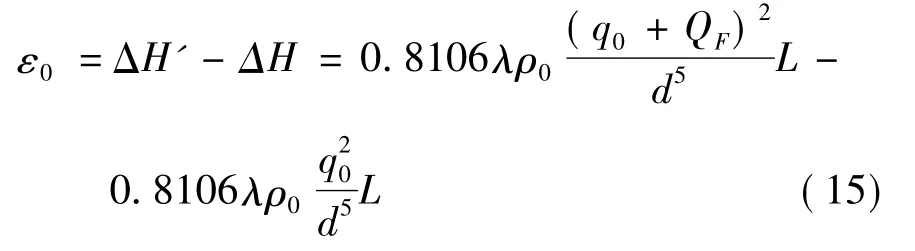
基于建模假设(3)，沿程损失系数λ仅与管壁相对粗糙度Δ/d有关。对于已建成的热力管网，管壁绝对粗糙度Δ和管径d为常数，可令管线阻抗 S=0.8106λρ0L/d5，忽略 QF二阶函数，可得:

则管线报警阀ε0可定义为

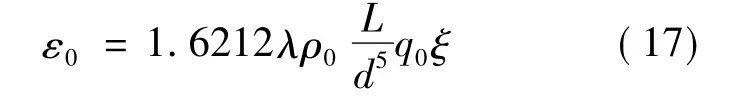
式中:ξ为衡量热力管网管线泄漏报警率的特征因子，称为灵敏度因子。ξ取值减小，报警阀ε0随之减小，这说明热力管网泄漏诊断的灵敏度升高，可导致热力管网故障诊断的误报率增加，反之亦然。因此，灵敏度因子ξ的选定是至关重要的。在下述算例中，灵敏度因子ξ=6，取自热力管网故障诊断系统的调试经验值。

2.2 泄漏点报警阀εF的定义

城市热力管网一般采用中压供暖，管线压力波动范围为3% ～5%。若管线出现泄漏点，则压力变化将超过该范围。故泄漏点报警阀εF可定义为管线i正常工作时虚拟泄漏点处压力值的4%，即

在定位泄漏点的过程中，采用黄金分割法插入泄漏点，所插入泄漏点的定位逻辑图如图3所示。

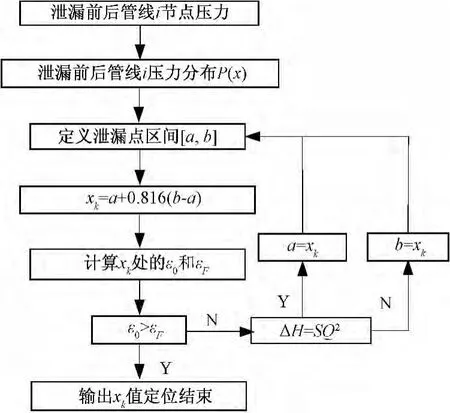
图3 泄漏管线泄漏点的定位逻辑图Fig．3 Logic diagram of leakage of pipeline leak location

3 算例及分析

3.1 管网正常运行状态的水力计算结果

热力管网正常运行时，所有节点的流量代数和为零，节点流量和压力数值如表1所示，管线计算流量和压降数值如表2所示。

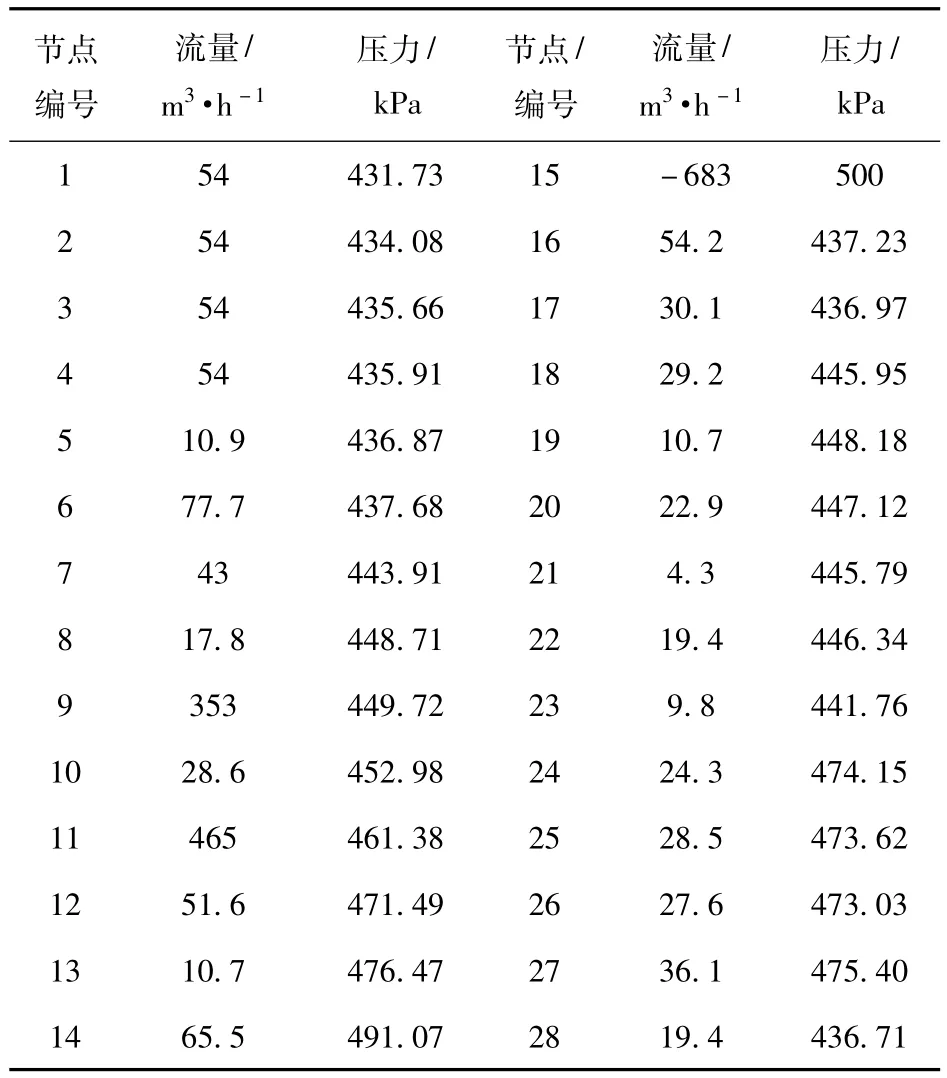
表1 管网正常运行状态时节点参数值Tab.1 Node parameter value of network normal operation

表2 管网正常运行状态时管线参数值Tab.2 Pipeline parameter value of network normal operation

3.2 管网泄漏故障状态的水力计算结果及分析

假设热力管网管线7上坐标为(294.85，904.44)点发生泄漏，泄漏量为5 m3/h，此时热力管网所有节点的流量代数和不为零，管网节点流量和压力数值见表3，管线计算流量和压降数值见表4，热力管网各管线报警阀ε0的取值与管线压降实际值和计算值的差值ε的比较结果见表5。由上述计算结果可知:

(1)管线7，13，18的压降实际值和计算值的差值ε均大于报警阀。由图1可以看出:管线13，18均位于管线7的上游，而管线泄漏搜索从最末端开始，且管线7单位长度压力损失变化率远大于管线13，18的压力损失变化率;依据判定标准，确定管线7上存在泄漏点;管线13，18出现的压力波动和供水量变化主要是由于下游泄漏点泄漏对上游管路的影响造成的，也不排除与计算时造成的舍入误差有关。

表3 管网泄漏故障状态时节点参数值Tab.3 Node parameter value of network leakage fault

表4 管网泄漏故障状态时管线参数值Tab.4 Pipeline parameter value of network leakage fault

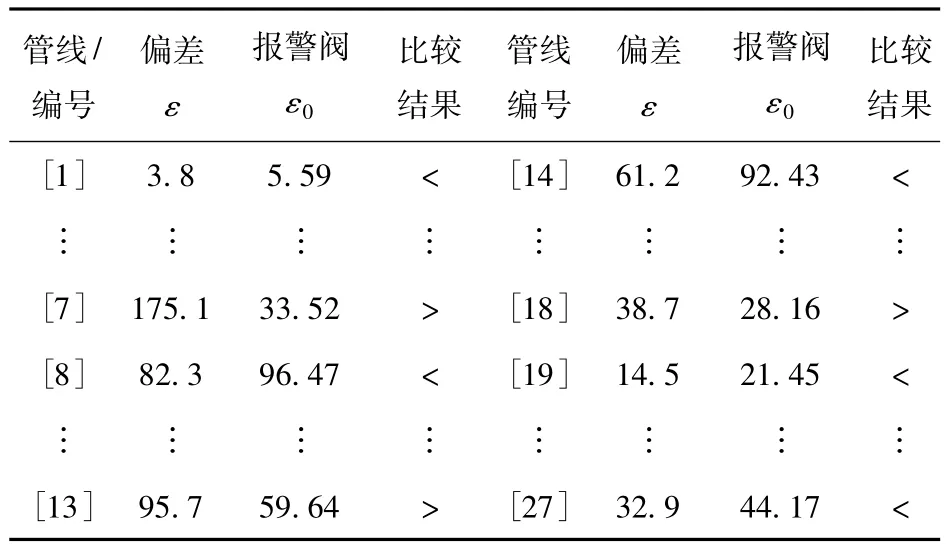
表5 ε0与ε比较结果Table．5 Comparison results of ε0and ε

(2)管线7的上游主干管线13出现压降实际值大于计算值的管线，且差值ε大于报警阀ε0，这是由于管网发生泄漏时，管线13较长，其累积压降大，因此出现报警;同时由于管线7的泄漏仅使上游支管流量略有增加，使得管线7上游各支管压降实际值近似等于计算值。

(3)管线7的下游管线的压降实际值近似等于计算值，这是供水量的补偿导致下游管线泄漏前后压降变化不大的结果。

作者所开发的热力管网故障诊断系统按图3所示逻辑可定位泄漏管线泄漏点，即xF=73.64，其所在的管线7长度L7=180 m。将其转换成地理图集上的坐标为(x1，y1)=(292.97，910.83)，假设的泄漏点坐标为(x2，y2)=(294.85，904.44)，则该系统定位的误差可按式(18)计算:

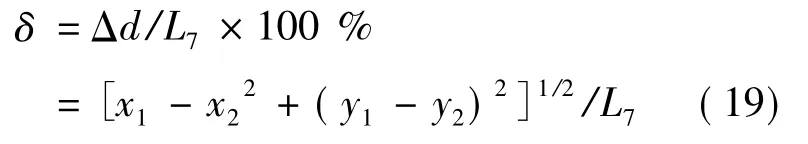
代入数据得δ=4.82%

可见系统泄漏点的定位误差在工程要求范围内。因此，本文所提出的枝状热力管网单点泄漏的故障诊断方法是合理的，具有一定应用价值[11，12]。

4 结论

(1)为某市热力管网建立了热力管网水力计算模型，以此为基础开发的热力管网故障诊断系统可确定泄漏点的大致位置，其定位误差在工程要求的范围内。因此，文中所提出的插入虚拟节点法及报警阀ε0，εF的值域的设定是合理的，具有一定的应用价值。

(2)泄漏管线对上游管线误报警有一定的影响，但也不排除与计算时造成的舍入误差有关，此点尚需进一步研究。

(3)本文的研究成果虽然仅适用于单点泄漏的枝状热力管网故障诊断，但对多泄漏点的热力管网可找出离末端最近的泄漏管线，具有一定的参考价值。

[1]Alan T．Murray，Tong Daoqin．GIS and spatial analysis in the media[J]．Applied geography，2009，(29):250－259．

[2]Lopes dos Santos P，Azevedo-Perdicou，Ramos J A，et al．An LPV Modeling and Identification Approach to Leakage Detection in High Pressure Natural Gas Transportation Networks[J]．IEEE Control Systems Society，2011，19(1):77－79．

[3]杨杰，王桂增．输气管道泄漏诊断技术综述[J]．化工自动化及仪表，2004，31(11):1－5．

[4]王瑛周，李春刚．SCADA技术在城市供水系统中的应用[J]．经济技术协作信息，2010，11(1030):198－199．

[5]陶建科，胡永清．基于GIS和SCADA技术的供水管网管理信息系统[J]．供水技术，2008，2(2):29－32．

[6]Zhang Yu，Liu Jian，Zeng Zhoumo．A combined kalman filter-Discrete wavelet transform method for leakage detection of crude oil pipelines[C]．Shanghai:ICEMI，2009:1086 －1090．

[7]卜月华．图论及其应用[M]．南京:东南大学出版社，2002．

[8]秦芳芳．供热管网水力计算模型研究[D]．保定:华北电力大学，2008．

[9]刘贤荣，倪鹏．外部多水源给水管网水力计算程序的应用[J]．华侨大学学报，2005，26(2):15－19．

[10]毕锋东，李树杰，陈久会，等．人工智能型管道泄漏监测系统在克—乌成品油管道的应用[J]．管道技术与设备，2005，22(6):22－24．