基于(2，1，7)卷积码实现低误码率通信的DSP设计*

王宏俊，杜长斌，杨自恒，丁 群

(黑龙江大学电子工程学院，哈尔滨150080)

基于(2，1，7)卷积码实现低误码率通信的DSP设计*

王宏俊，杜长斌，杨自恒，丁 群*

(黑龙江大学电子工程学院，哈尔滨150080)

为降低数字通信系统传输差错并提高可靠性，从工程应用角度出发，在DSP硬件平台上实现(2，1，7)卷积码。用MATLAB仿真影响(2，1，7)卷积码性能的各个参数，与约束度为3和码率为3/4、2/3的卷积码进行对比，其仿真结果为DSP硬件实现奠定理论基础。最后选用TI公司的TMS320DM6437型号，在CCS3.3开发环境上运行。实验表明:约束度为7、码率为1/2的卷积码在较低的信噪比(SNR=6 dB)下误码率则可达到10-6，且DSP实现的(2，1，7)卷积码方便可行，快速稳定，译码准确，并具有较强的纠错能力。

信道编码;(2，1，7)卷积码;DSP实现;低误码率;约束长度;码率;MATLAB仿真

信道编码是数字通信系统的重要组成部分。在通信系统中，信道传输特性不理想以及噪声的存在，会导致接收端出现接收信号的错误，因此用于信道纠错的信道编码是数字通信系统中极为重要的一个环节。

常用的纠错编码按其码字结构形式和对信息序列处理方式的不同可分成两大类:分组码和卷积码。在分组码的一个码组内，监督校验位r仅与本码组内的k个信息码元有关，而与其他码元无关，这种信息序列处理的方式称为分组码。卷积码是伊利亚斯于1955年提出的，卷积码编码时充分利用了各信息组之间的相关性，即编码器对每一个长度为k的信息码元产生长度为n的码组(又称作子码)。子码中的校验元，不仅与本子码的k个信息码元有关，而且还与此前m个子码中的信息码元有关［1］。然而，在与分组码同样的码率R和设备复杂度的条件下，无论在理论上还是从实际上均已证明卷积码的性能优于分组码，且实现最佳译码也较分组码容易［2］。

针对卷积码的优良特性，国内外学者开展了广泛的研究。但一般多为理论上的编译码原理推导，并只局限在MATLAB、System View等工具的软件仿真，如文献［3］提出的卷积码的System View实现，文献［4］提出的卷积编码及其维特比译码算法的软件实现等。尽管文献［5］提出了卷积码的DSP实现，但约束度仅为3，不能满足实际应用需要。本文以软件无线电为研究背景，兼顾综合译码的复杂度和纠错能力，选用(2，1，7)“NASA”卷积码，用MATLAB仿真工具准确计算出经过高斯信道、不同信噪比下的误码率，并绘制出误码率曲线。

1 系统总体概述

DSP是软件无线电(SDR)必需的基本器件，是其灵魂和核心所在。在发送端，将待发送的模拟音频或视频信号经过视频转换芯片进行数字化，送入DSP进行压缩和卷积编码处理，DSP通过其外部存储器接口EMIF与FPGA相连，FPGA作为协同处理器，主要完成数据的扩频、BPSK调制等工作，D/A模块将调制后的数字信号转换成模拟信号后经RF无线射频发射出去。

接收时，来自天线的信号经过RF处理和变换，然后通过FPGA模块进行解调，在DSP模块中解压缩和维特比译码，处理后的数据送至多功能用户终端。工作框图如图1所示。

图1 系统工作原理图

2 (2，1，7)卷积编、译码原理及仿真

2.1 (2，1，7)卷积码编码器

图2给出了二进制卷积码的编码器例子。

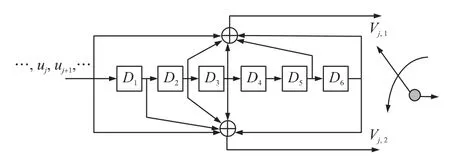
图2 (2，1，7)卷积码编码器

图中 D1D2D3D4D5D6为移位寄存器(D触发器)，信息序列从左面输入，编码器的工作受时钟脉冲控制。在每个时钟脉冲到来时输入一个信息码元，例如第j个时钟脉冲送入uj，下一个时钟脉冲，即第j+1个时钟脉冲送入uj+1，······移位寄存器中的存储数据在每个时钟作用下右移一位，则当输入信息码元为uj时，D1D2D3D4D5D6中分别存放着此前输入的uj-1，uj-2，uj-3，uj-4，uj-5，uj-6，经运算可得到两个校验元vj，1和vj，2，

在编码器输出端，由旋转开关实现并/串转换，每个时钟周期输出一个子码，例如第j个时钟脉冲输出子码cj=(vj，1，vj，2)。显然cj中的校验元vj，1和vj，2不仅与 uj有关，同时还与 uj-1，uj-2，uj-3，uj-4，uj-5，uj-6有关，即与此前m=6个子码中的信息元有关。且每一个信息元，如uj，经过6个时钟周期后，其对校验元vj，1和vj，2的影响将消失。由此可见，m =6为编码存储，表示信息组在编码器中的存储周期［6］。

同理可知，第j+1个时钟周期将输出子码cj+1=(vj+1，1，vj+1，2)，其中

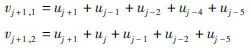
因此，卷积码的每个信息元，不但参与决定本子码的校验元，还要参与决定其后续子码的校验元。这就是说，信息码元使前后相继的子码之间产生约束关系，即子码之间存在相关性［1］。不难看出，第j个时钟周期输入的信息码元uj，仅在子码cj，cj+1，cj+2，cj+3，cj+4，cj+5，cj+6中出现，在cj+7中就没有uj的影响了。换言之，信息码元 uj把 cj，cj+1，cj+2，cj+3，cj+4，cj+5，cj+67个子码联系在一起，这7个子码之间存在相关性［7］。通常用编码约束度N表示子码之间的这种关联关系，显然N=m+1=7。以上编码器输出的每个子码，信息位数k=1，输出码组长n= 2，码率k/n=1/2，一般表示为(2，1，7)卷积码。其中，码率和约束度是衡量卷积码的两个重要参数。

2.2 (2，1，7)编码器的MATLAB仿真

设输入信息序列u=(1 1 1 0 1 0 1 0 0 1)，计算得c=(1 1 1 0 0 1 0 1 1 1 0 0 0 1 1 1 0 0 1 0)，在MATLAB中仿真得到的结果为图3所示。MATLAB命令窗口显示的编码输出为

图3 MATLAB仿真卷积编码输出序列

在这里注意到，输入序列u=(1 1 1 0 1 0 1 0 0 1)只有10比特，而发送的码序列却包含了32比特，码率并不是1/2。这是由于编码器有m=6个记忆单元，编码器必须“刷新”其缓存器才能完成码序列，子码序列中最后多余的12比特即对应于编码移位寄存器的清空过程。因此，虽然理论值的码率为1/2，但有效码率却是10/32=5/16，这种码率的降低称为分数码率损失。如果使用码率为R，而记忆深度为M的卷积码发送一条包含K个信息比特的消息是，有效码率为［8］

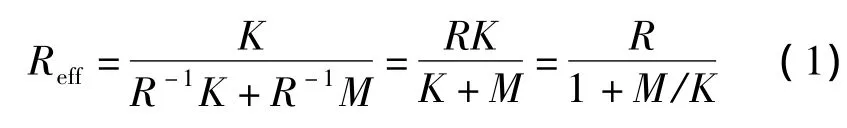
因此，卷积码在K≿M(K远远大于M)时最有效，即待发送的信息序列长度远大于寄存器的存储长度。在此条件下，有效码率渐进的达到该码先前定义的本身的码率R。

2.3 维特比译码原理分析与MATLAB仿真

维特比译码算法是一种最大似然译码算法，该算法译码速度快，译码器也相对简单，是一种很有效的译码方法，目前广泛的应用于各种数字传输系统。

Viterbi译码的详细原理参见文献［2］，这里只作简单介绍。Viterbi算法的基本思想就是利用网格图，在众多的竞争路径中搜索一条最接近接收信息的路径，称之为幸存路径。对于(2，1，7)卷积码，共有26种状态，在每一个译码时刻t，每个状态节点都向外送出2条路径，同时也接收2条来自其他节点的路径［9］。在接收到的2条路径中，将累积度量值最小的一条保留下来，而将另一条路径淘汰。因此，在每个译码周期中只保留64条幸存路径，任意一条幸存路径代表一个确定的译码输出。

一个完整的Viterbi译码器一般包括以下7个部分:状态发生器、累加器、比较器、度量值寄存器、幸存路径寄存器、判决器、控制电路等［10］，如图4所示。

图4 维特比译码器基本结构

这些步骤就构成了维特比算法，将编码输出结果作为译码器的输入，MATLAB仿真结果如图5所示。

图5 MATLAB仿真译码器输出

3 基于MATLAB的(2，1，7)卷积码性能分析

本节为体现(2，1，7)卷积码优越的性能，对不同码率、不同约束度、不同回溯长度的卷积码进行分析、仿真和比较。得出的结论是:码率越低，性能越好;约束度越大，系统性能越好，但是会提高系统的复杂性。最终兼顾复杂性和可靠性，选择码率为1/2，约束度为7的(2，1，7)卷积码，为DSP的实现奠定了夯实的理论基础［11］。

3.1 卷积编码对系统性能的影响

图6给出了不同信噪比下，发送10 000比特的卷积编码的蒙特卡洛仿真结果，可以直观的看出:经过(2，1，7)卷积编码可以降低数字通信系统的误码率，从而提高了系统的可靠性。

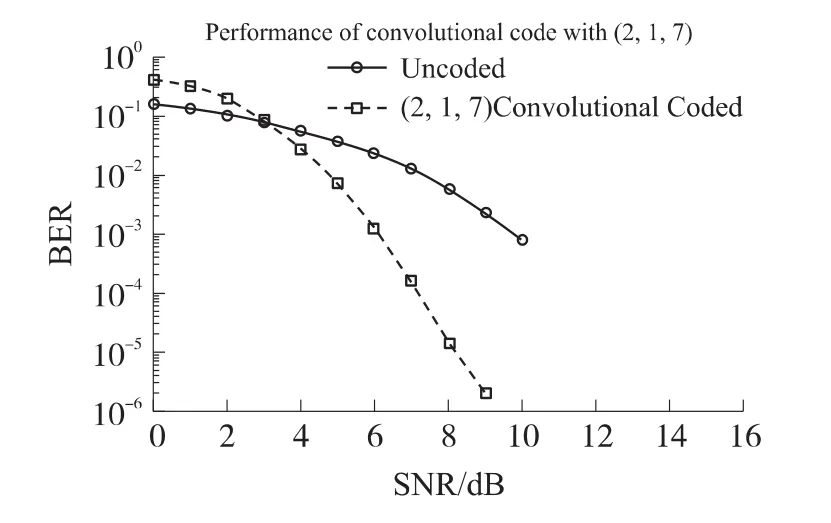
图6 未编码与卷积编码系统的误码率比较

从图中可以看出，当信噪比较小时，未编码的误码率反而比采用编码的误码率低，这是因为误比特太多导致接收到的信息几乎无效。但是当信噪比稍高后卷积编码的误码率就大大降低了。

3.2 码率对卷积码性能的影响

卷积码的码率R=k/n，它是卷积码的一个重要参数。当改变卷积码的码率时，系统的误码性能也将随之发生变化，仿真结果如图7所示。

观察图7可以得出如下结论:当改变系统码率时，随着卷积码码率的逐渐提高，系统的误码率也呈现出增大的趋势，也就是说，码率越低，系统的误码率就越小，误码性能就越好。

图7 不同码率对卷积码性能的影响

3.3 约束度对卷积码性能的影响

对于码率一定的卷积码，当约束度N发生变化时，系统的误码性能也会随之发生变化。仿真如图8所示。

图8 不同约束度对卷积码性能的影响

从图8中可以清楚地看到:在低信噪比时，(2，1，3)卷积码的性能优于(2，1，7)卷积码，但此时二者的误码率都非常高，在工程上无法实际应用。当信噪比高于一定值后，(2，1，7)卷积码的性能快速优于(2，1，3)卷积码。所以说当码率一定且信噪比高于一定值时，增加约束度可以明显降低系统的误码率。但是随着约束度的增加，译码设备的复杂性也会随之增加。所以对于码率为1/2的卷积码，我们在选取约束度时一般为3～9。

3.4 回溯长度对卷积码性能的影响

回溯长度是在Viterbi译码过程中一个很重要的参数，它决定了维特比译码的精度，同时也影响着译码延迟，随着它的不断变化误码性能也随之改变［12］。

将反馈深度分别取值为9，19，30和35。仿真结果如图9所示。

图9 不同回溯长度对卷积码性能的影响

从图9中的误码率曲线可以清楚地看到:当回溯长度逐渐增加，系统的误码率随之逐渐降低，但是当回溯程度增加到5N时(N为编码的约束度)，误码率数值变化不大，这里的(2，1，7)卷积码在回溯长度达到35左右基本趋于稳定。因此在选取回溯长度时，通常取回溯长度为5N。

3.5 MATLAB实现的(2，1，7)卷积码低误码率性能仿真

在MATLAB仿真测试中，信源为随机产生的10 000个二进制码元，经过卷积编码后进入高斯信道，然后经过卷积译码后进入信宿，流程图如图10所示。

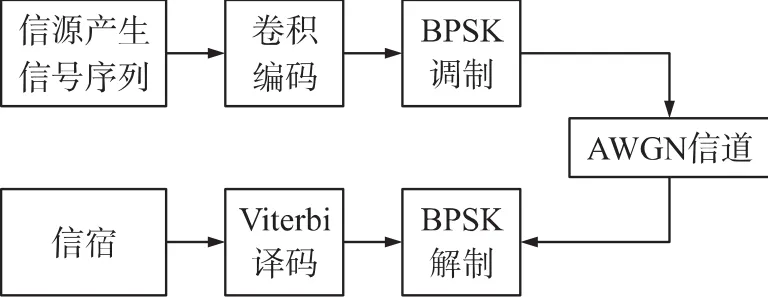
图10 MATLAB仿真(2，1，7)卷积码流程图

在接收端计算误码率，不同系统的误码率的比较如表1所示。

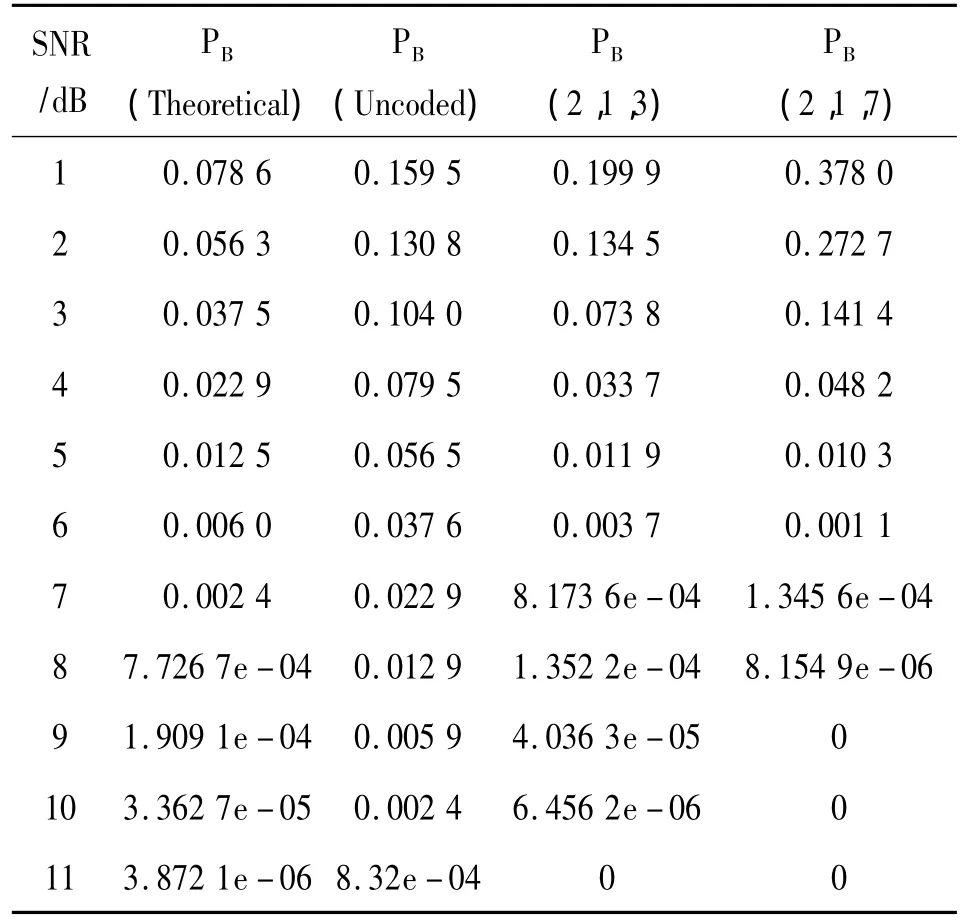
表1 误码率的比较

通过对比以上数据可以得出:经过卷积编码的系统在信噪比 SNR=8 dB时，误码率已经达到10-6，而未经编码的系统若达到相同的误码率则信噪比至少需要提高一倍，由此可见卷积编码对系统误码率的影响。同时，经过观察数据也可发现，当信噪比SNR＞4 dB后，(2，1，7)卷积码的误码率明显优于(2，1，3)卷积码，且快速下降到10-6及以下。由此也可以看出，(2，1，7)卷积码符合工程需要，可以在DSP上运行实现，仿真图如图11所示。

图11 (2，1，7)卷积码性能比较图

4 (2，1，7)卷积码的DSP实现

基于各种考虑，选择在TI的TMS320DM6437上实现卷积码的编译码。C64X+系列DSP具有很高的操作灵活性和速度。它具有先进的修正哈佛结构、专门硬件逻辑的CPU、片内存储器、片内外设和专用的指令集，同时C64X+系列的螺旋结构能够将DSP的CPU和片内存储器与外设配置组合在一起，可满足电子市场众多领域的应用要求［10］。

4.1 卷积码编码的DSP实现

(2，1，7)卷积码的生成多项式为:

其中，D表示时钟延迟。编码原理不再赘述，主要的变成思路如下:

(1)定义数据长度、编码码率、编码延迟寄存器深度和输入待编码信息;这里取输入数据为:

UcInput［9］={0x07，0x4b，0x55，0x6c，0x47，0x36，0xb4，0x47，0x53}

(2)输入的数据打包为byte的数据，将byte数据的每一位取出来;

(3)初始化卷积编码延迟寄存器;

(4)根据(2，1，7)卷积码的生成多项式对每个数据进行卷积编码，并将编码结果输出到outbuffer;

(5)将卷积结果输出。

在CCS3.3环境运行结果如下所示:

4.2 维特比译码的DSP实现

编程思路如下:

(1)大致同编码步骤1，定义数据长度、编码码率、编码延迟寄存器深度，以及译码节点状态数。

(2)维特比译码，具体流程如图12所示。

图12 译码流程图

(3)回溯过程，获得保留的最大似然路径。

第1步，先从最后一个数据节点取出最大状态度量值的状态，以此为回溯起始状态;

第2步，根据保留路径获得每个节点的数据。(4)输出译码结果如下所示。

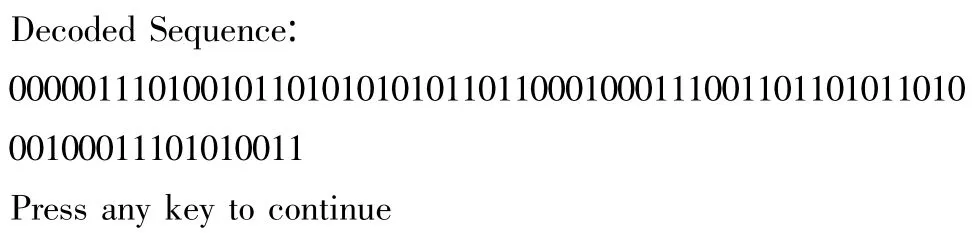
从译码结果中可以看出，其输出与原始数据完全一致，可见译码正确。

4.3 卷积码的纠错能力验证

对于卷积码，没有明显的分组结构，纠错能力无法像分组密码那样简洁的描述出来，这里用df(自由距离)表示纠错比特个数t:

完整的说法是:采用最大似然译码时，卷积码能在3～5个约束度内纠正t个错误。本文中约束度为7，则可以理解为21比特～35比特内可纠正t个错误。在(2，1，7)卷积码中，自由距离df=10，则t应取不超过的最大整数4。

为验证卷积码的纠错能力，编写了一段测试程序:

(1)首先对输入数据进行编码ConvoCodingTail_1(ucInput，cViterbiInTmp，DATA_LEN+4);

(2)然后对输出数据进行译码ViterbiDecSs_1(cViterbiInTmp，cDecOut，DATA_LEN);

(3)将译码输出结果与输入数据进行比较，如果不相同，输出"FAIL";相同则输出"SUCCESS"，同时将译码结果显示出来。

在该测试实验过程中，随机修改卷积编码输出序列中的个别比特值，以模拟高斯信道中的突发差错，然后再进行译码。若译码成功，则继续添加该输出序列中的错误比特，直至译码失败。经多次测试，反复试验，得出数据如表2所示。

表2 测试(2，1，7)卷积码纠错能力总结表

分析上表可知，该卷积码大约能够在4.3个约束度内纠正4个随机错误，提高了系统的纠错能力，达到了信道编码的目的。

5 总结

基于DSP实现的(2，1，7)卷积码性能优良，系统运行稳定、高效，且经(2，1，7)卷积编码输出的信息比特误码率在低信噪比下仍能达到10-6，且具有较好的纠错能力，大大增强了信道抗干扰能力，是目前国际卫星通信和其他通信系统中广泛使用的一种标准卷积码。

［1］孙丽华，谢仲华，陈荣伶.信息论与纠错编码［M］.北京:电子工业出版社，2005:191-201.

［2］张博.卷积码的译码研究及DSP实现［D］.硕士论文，天津大学，2008:1-3.

［3］李晓瑞，张毅，徐伯庆.卷积码的System View实现［J］.仪器仪表学报，2005，26(增刊):488-490.

［4］刘少阳，邹永.(2，1，7)卷积编码及其维特比译码算法的软件实现［J］.信息与电子工程，2006，4(6):467-469.

［5］Hasnain SK，Beg A，Monir SM G.Performance Analysis of Viterbi Decoder Using a DSP Technique［C］//Proceedings of INMIC 2004 8th International Conference，2004:201-207.

［6］Mohamed F M，AhmedH Tewfik.Convolutional Decoding in the Presence of Synchronization Errors［J］.IEEE Journal on Selected Areas in Communications，2010，28(2):218-227.

［7］Richard BWells.工程应用编码与信息理论［M］.尹长川，罗涛，腾勇，译.北京:机械工业出版社，2003:167-170.

［8］Hocevar D E，Gatherer A.Achieving Flexibility in a ViterbiDecoder DSP Coprocessor［C］//Vehicular Technology Conference，2000:2257-2264.

［9］黄肖玲，杨华龙.大约束度卷积码快速译码方法的研究［J］.通信学报，2010，31(3):57-64.

［10］Mohamad R，Anas N M.Performance Analysis of Convolutional Interleaver on TMS320C6711 Digital Signal Processing Kit［C］//International Conference on Computer Applications and Industrial E-lectronics(ICCAIE)，2010:516-520.

［11］于沛东，李静，彭华.一种利用软判决的信道编码识别新算法［J］.电子学报，2013，41(2):301-306.

［12］詹明，周亮.一种基于对称性的双向双二进制卷积Turbo码译码结构研究［J］.电子与信息学报，2012，34(5):1179-1184.

DSP Design Based on the(2，1，7)Convolutional Code to Achieve Low Error Rate Communication*

WANG Hongjun，DU Changbin，YANG Ziheng，DINGQun*
(Electronic Engineering College，Heilongjiang University，Harbin 150080，China)

In order to reduce transmission errors in digital communication systems，and enhance the reliability of the channel，from the perspective of engineering application，DSP technology is utilized to achieve(2，1，7)convolutional code.Using MATLAB to simulate the factor of affecting(2，1，7)convolutional code performance and compare that with convolutional code of constraint length 3 and code rate 3/4，2/3 respectively，the result lays the theoretical foundation for hardware implementation.Finally，TICompany’s TMS320DM6437 is applied to run in CCS3.3 environment.The experiment shows that after convolutional code of constraint length 7 and code rate 1/2，error code rate can still achieve 10-6in lower SNR(SNR=6 dB).And DSP hardware implementsworks easily，operates stably and fast，decodes correctly and has a strong error correction capability.

channel coding;(2，1，7)convolutional code;DSP implement;low error rate communication;constraint length;code rate;MATLAB simulation

10.3969/j.issn.1005-9490.2014.01.024

TN914.31 文献标识码:A 文章编号:1005-9490(2014)01-0097-06

项目来源:国家自然科学基金项目(61072072);黑龙江省高校“现代传感技术”创新团队项目(2012TD007)

2013-05-03修改日期:2013-06-07

EEACC:6210B;6150

王宏俊(1989-)，女，汉族，黑龙江省佳木斯市人，黑龙江大学电子工程学院，硕士研究生，研究方向信息处理与保密通信，yyxzj_love@126.com;

丁 群(1957-)，女，汉族，黑龙江省哈尔滨人，黑龙江大学电子工程学院，教授，博士生导师，研究方向信息安全与保密通信，qunding@aliyun.com。