(101)单轴应力对Si材料电子电导率有效质量的影响*

乔丽萍，王聪华，李淑萍，李 丽，俞丽娟，何 磊

(1.西藏民族学院信息工程学院，陕西咸阳712082; 2.西安电子科技大学微电子学院，宽禁带半导体材料与器件教育部重点实验室，西安710071)

(101)单轴应力对Si材料电子电导率有效质量的影响*

乔丽萍1，2*，王聪华1，李淑萍1，李 丽1，俞丽娟1，何 磊1

(1.西藏民族学院信息工程学院，陕西咸阳712082; 2.西安电子科技大学微电子学院，宽禁带半导体材料与器件教育部重点实验室，西安710071)

由Schrödinger方程出发，基于(101)单轴应力下Si材料导带E-k解析模型，重点研究沿任意晶向(101)单轴应力对Si材料电子电导率有效质量的影响。结果表明:(101)单轴应力沿0°和45°晶向均导致导带底附近的六度简并能谷分裂成两组分立的能谷;(101)单轴张应力下，沿45°晶向的电子电导率有效质量随应力增大而明显减小，沿0°和90°晶向的电子电导率有效质量随应力增大而明显增大;(101)单轴压应力下，Si材料沿高对称晶向的电子电导率有效质量随应力增大而明显增大或几乎不变。

应变张量;简并度;晶向;张应力

将单轴应变技术与半导体Si材料相结合，可有效提高Si材料的电子迁移率，这有利于Si基应变器件的性能提升。因此，该技术已大量应用于高速/高性能半导体器件和集成电路中［1-4］。对于单轴应变的Si器件来说，应变导致材料能带结构改变和载流子迁移率提高［5-6］，而Si材料载流子迁移率的变化又与电子电导率有效质量的变化存在密切的联系。基于上述原因，讨论单轴应力对Si材料电子电导率有效质量的影响具有重要的理论意义和实用价值。

对于上述领域，目前国内外的学者主要将研究重点集中在单轴应变Si电子迁移率上［7-9］，涉及到求解过程中各重要物理参量的文献较少。其中，对(101)单轴应变Si材料电子电导率有效质量的研究仍然存在不足，这不利于明确(101)单轴应力对Si材料电子电导率有效质量的影响，以及进一步理解导致电子迁移率增强的物理机制。

本文针对单轴应变Si(101)晶面，由薛定谔方程出发，基于(101)单轴应力下的Si材料E-k解析模型，获取了(101)单轴应变Si材料的各重要物理参量，包括导带能谷能级、简并度与应力强度以及施力角度之间的关系。并在此基础上，进一步揭示了(101)单轴应力作用下，不同晶向上的Si材料电子电导率有效质量与应力类型及应力强度的关系。本文所得模型与数据，为研究(101)单轴应力对Si材料电子电导率有效质量乃至电子迁移率的影响提供了理论依据。

1 (101)单轴应变Si导带结构模型

1.1 应变张量模型

应变张量是研究建立(101)单轴应变Si导带结构模型的关键之一。如图1所示，初基原胞坐标系为(x，y，z)，所施应力T在(10)面内(为讨论方便而选取)，辅助坐标系(x'，y'，z')的x'轴垂直于(10)面，z'轴沿着应力T所在的方向。在坐标系(x'，y'，z')内，应力张量可表示为:

从辅助坐标系(x'，y'，z')到初基原胞坐标系(x，y，z)的转换矩阵为:

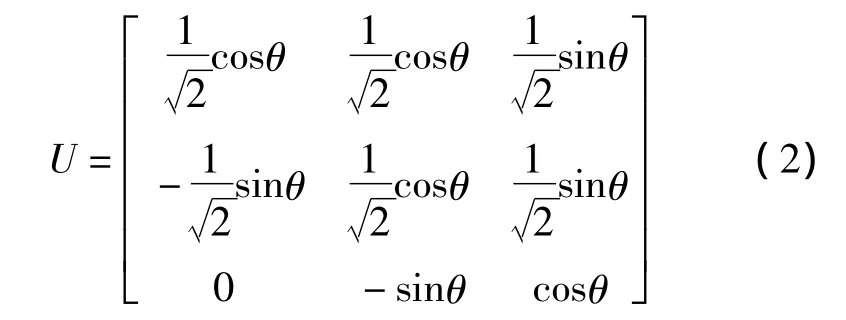
式中θ为方位角，即为z'轴与z轴的夹角。

式中，T为应力强度，θ为(101)面内施加应力的角度，c11，c12，c44为弹性劲度系数，上述物理参量可由参阅文献［10］获得。

图1 (101)面施加单轴应力示意图

1.2 (101)单轴应变Si E-k关系

研究单轴应力对Si材料电子电导率有效质量的影响，必须建立单轴应力下Si材料导带E-k模型。单电子近似单轴应变Si材料Schrödinger方程为［11］:

其中，Uunstrain(r)是弛豫Si材料的晶格周期性势场，UDeformation(r)是晶格形变势场。

使用零级波函数，在单轴应变Si导带6个能谷极值中的任意一个ki0(i=1～6)处将unk展开，式(1)变换为，

其中，

基于微扰理论，单轴应变Si材料导带E-k模型由式(2)建立，

其中，Uki0通过形变势理论获得，

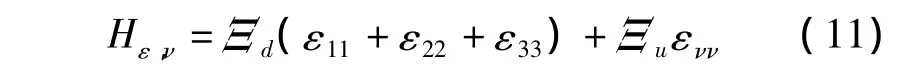
对于v=1，2，3，ε11，ε22，ε33，ε12为应变张量，Ξd和Ξu为形变势常数，表达式见2.1节。

2 电子电导率有效质量分析

2.1 导带简并度及能级

确定(101)单轴应变Si电子电导率有效质量，还需要明确单轴应力下Si材料能带能谷简并度和能级。基于(101)单轴应力下Si材料导带E-k解析模型，应变Si导带能谷能级与应力强度及受力角度的关系如图2所示。

为了便于分析，图3进一步给出了(101)单轴应力下Si材料导带能谷简并度与应力强度及受力角度的关系。由图3(a)可以清楚地分析得出，施加单轴张应力时，导带带边简并度随受力晶向变化情况为2°→4°→2°;施加单轴压应力时(见图3 (b))，导带带边简并度随受力晶向变化情况为4°→2°→4°。

图2 导带能谷能级与应力大小及角度的关系

图3(c)是沿(101)面45°晶向施加单轴应力时，单轴应力下Si材料导带能谷简并度及能级与应力强度及类型的关系。由图分析得出，由于应变导致导带底附近的六度简并能谷分裂成两组分立的能谷:一组为二重简并能谷Δ2(［001］、［001］方向能谷)，另一组为四重简并能谷 Δ4(［100］、［100］、［010］、［010］方向能谷)。其中，张应力作用时，Δ2、Δ4能谷能量极小值均增大，Δ4增加量小于Δ2，成为导带带边。压应力作用时，Δ2、Δ4能谷能量极小值均减小，Δ2减小量大于Δ4，成为导带带边。

图3(d)是沿(101)面0°晶向施加单轴应力时，单轴应力下Si材料导带能谷简并度及能级与应力强度及类型的关系。由图分析得到与图3(c)类似情况，由于应变导致导带底附近的六度简并能谷分裂成两组分立的能谷:一组为二重简并能谷 Δ2(［010］、［010］方向能谷)，另一组为四重简并能谷Δ4(［001］、［001］、［100］、［100］方向能谷)。其中，张应力作用时，Δ2能谷能量极小值减小，成为导带带边，Δ4能谷能量极小值增大。而压应力作用下，Δ4能谷能量极小值减小，成为导带带边，Δ2能谷能量极小值增大。

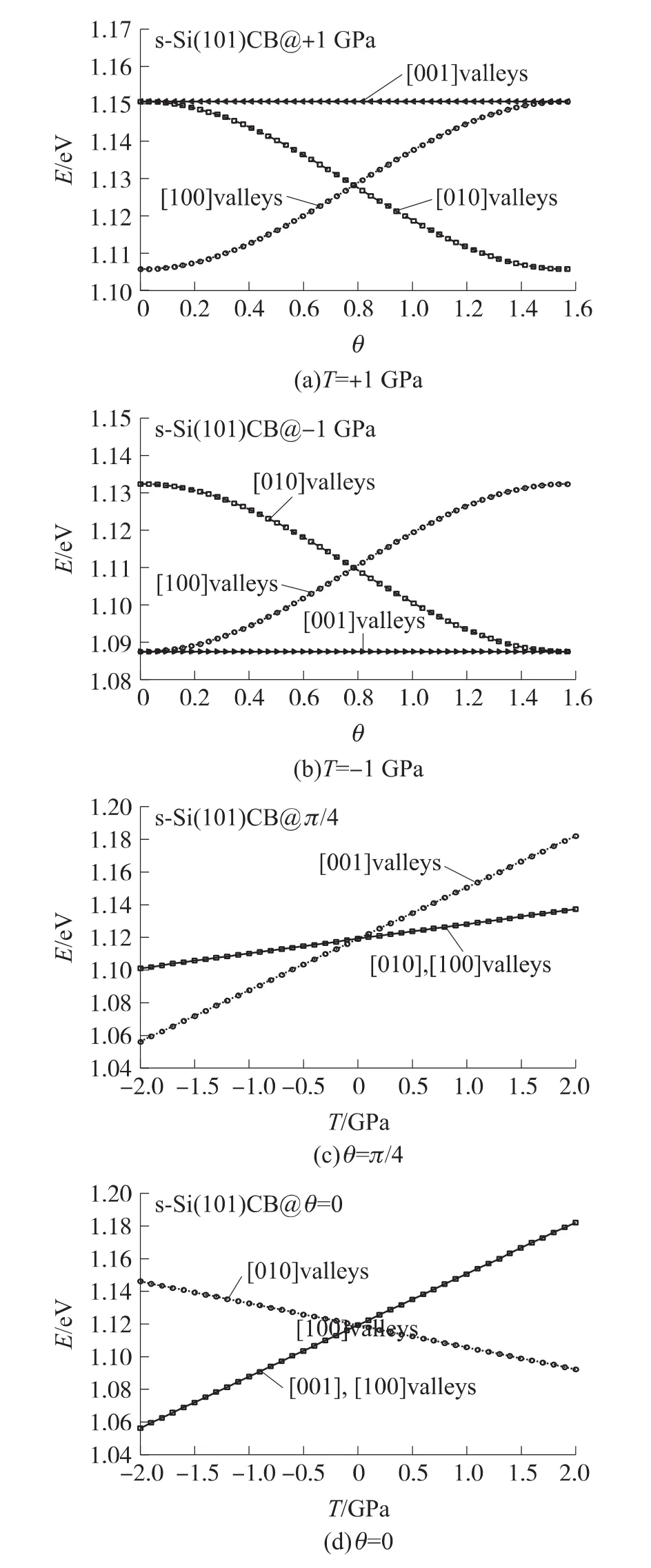
图3 导带能谷简并度与应力大小及角度的关系

2.2 (101)单轴应力下电子电导率有效质量

基于已获得的单轴应力下Si材料导带E-k关系、能谷简并度及能级模型，采用类似GaAs的处理方案，可得单轴应变Si材料的(101)晶面任意晶向电子电导率有效质量mc的模型为:

其中，mlow为低简并能谷电导有效质量，mhigh为高简并能谷电导有效质量，μhigh为高简并能谷迁移率(i =1，2，分别表示次高和最高能谷)。

图4 电子电导率有效质量与应力大小及角度的关系

(101)单轴应力下Si材料电子电导率有效质量mc与应力强度及受力角度的关系如图4所示。由图分析可知，施加单轴张应力时，Si材料(101)面内，沿45°晶向的电子电导率有效质量mc随应力增大而明显减小，沿0°和90°晶向的电子电导率有效质量mc随应力增大而明显增大。而在施加单轴压应力情况下，Si材料沿(101)面内高对称晶向的电子电导率有效质量mc随应力增大或明显增大或几乎不变。应力致电子电导率有效质量变化情况比较可知，单轴张应力致电子迁移率增强，施加应力沿45°晶向。

3 结论

本文从薛定谔方程出发，结合应变张量理论，建立了(101)单轴应力下Si材料导带E-k解析模型，并由此进一步获得了(101)单轴应力下Si材料导带能谷能级、简并度与应力强度及受力角度的关系，并最终建立了(101)单轴应变Si任意晶向电子电导率有效质量与应力强度和应力类型的关系模型。研究结果表明:(101)单轴张应力下，沿45°晶向的电子电导率有效质量随应力增大而明显减小，因此单轴应力致电子迁移率增强的应力类型应选择沿45°晶向的张应力。

［1］Knoll L，Zhao Q T，Nichau A，et al.Inverters with Strained Si Nanowire Complementary Tunnel Field-Effect Transistors.IEEE E-lectron Device Letters，2013，34(6):813-815.

［2］Yu W，Zhang B，Zhao T，et al.Hole Mobilities of Si/Si0.5Ge0.5 Quantum-Well Transistor on SOIand Strained SOI.IEEE Electron Device Letters，2012，33(6):758-760.

［3］Gomez L，Hashemi P，Hoyt JL.Enhanced Hole Transportin Short-Channel Strained-SiGe p-MOSFETs［J］.IEEE Trans Electron Devices，2009，56(11):2644-2651.

［4］Feste S F，Knoch J，Habicht S，et al.Silicon Nanowire FETs with Uniaxial Tensile Strain［J］.Solid-State Electron，2009，53(12): 1257-1262.

［5］Li H，Xu Y，Xu Y，et al.Strain Effect Analysis on the Electrical Conductivity of Si/Si(1-x)GexNanocomposite Thin Flms［J］.Solid-State Electronics，2013，85:64-73.

［6］周春宇，刘超，石松宁，(111)Si基应变材料本征载流子浓度［J］.固体电子学研究与进展，2011，31(4):359-362.

［7］Jeon YW，Ka D H，Yu CG，et al.NBTIand Hot Carrier Effect of SOIp-MOSFETs Fabricated in Strained Si SOIWafer［J］.Microelectronics Reliability，2009，49(9):994-997.

［8］Kolomotes V，Baidakov V，Fedosov A.Application of Piezoresistance Effect in Highly Uniaxially Strained p-Si and n-Si for Current-Carrier Mobility Increase［J］.Physica Status Solidi B，2009，246(3):652-654.

［9］Ma X B，LiuW L，Liu X Y，etal.Strain Stability and Carrier Mobility Enhancement in Strained Si on Relaxed SiGe-on-Insulator［J］.Journal of the Electrochemical Society，2010，157(1):104 -108.

［10］宋建军，张鹤鸣，胡辉勇，等.四方晶系应变Si空穴散射机制［J］.物理学报，2012，61(5):57304.

［11］Song JJ，Yang C，Zhang H M，etal.Longitudinal，Transverse，Density-of-States，and Conductivity Masses of Electron in(001)，(101)and(111)Biaxially-Strained-Si and Strained-Si1-xGex，Science in China［J］.Physics Mechanics and Astronomy，2012，55 (11):2033-2037.

(101)Uniaxial Stress Effect on Electronic Conductivity Effective Masses of SiMaterials*

QIAO Liping1，2*，WANG Conghua1，LIShuping1，LILi1，YU Lijuan1，HE Lei1
(1.School of Information Technology，Tibet University for Nationalities，Xianyang Shanxi712082，China; 2.Key Lab ofWide Band-Gap Semiconductor Materials and Devices，School of Microelectronics，Xidian University，Xi’an 710071，China)

Based on the theories of strain tensor，the E-k relation for conduction band in uniaxial strained Si(101) materialswas established by Schrödinger equation.And then themodel of electronic conductivity effectivemass along arbitrary crystal direction in uniaxial-strained Si(101)is obtained.According to results，(101)uniaxial Stress causes six degrees of degeneracy of valley near the bottom of the conduction band splitting into two groups of discrete energy valley;electronic conductivity effectivemasses obviously decreases along 45°direction but increases along 0°and 90°directions，with increasing(101)uniaxial tensile stress;electronic conductivity effective masse of Si material along highly symmetric directions obviously increases or almost remains unchanged，with increasing(101) uniaxial press stress.The above results can provide valuable references for the study on strain Simaterial and the conduction channel design related to stress and orientation in the Si-based strain nMOSFETs.

strain tensor;degeneracy;crystal direction;tensile stress

10.3969/j.issn.1005-9490.2014.01.003

TN304.2 文献标识码:A 文章编号:1005-9490(2014)01-0009-04

项目来源:国家自然科学基金面上项目(61162025);西藏民族学院青年学人培育计划项目(13myQP08);重大项目培育计划项目(12myZP02);重点项目(11myZ04)

2013-07-11修改日期:2013-08-09

EEACC:7280;7125

乔丽萍(1982-)，女，陕西咸阳人，西藏民族学院讲师，西安电子科技大学在读博士，研究方向为射频电路设计及新型半导体材料及器件。