最小二乘支持向量机在线建模在预测控制中的应用*

洪 洲

(广州城市职业学院信息技术系，广州510405)

最小二乘支持向量机在线建模在预测控制中的应用*

洪 洲*

(广州城市职业学院信息技术系，广州510405)

针对智能预测控制中的预测模型，提出了最小二乘支持向量机(LS-SVM)在线模型的递推算法，减少了矩阵求逆计算。当模型达到较高的精度后，每次迭代过程中当一个新的数据点加入到数据集，则把具有最小|αi|的数据点删除。不但解决了数据集规模的问题，而且提高了预测模型的精确性。通过仿真验证了基于在线LS-SVM模型的预测控制可以使系统快速、准确地跟踪期望输出，达到预期的控制效果。

LS-SVM;在线建模;预测控制;预测模型

预测模型在工业过程的预测控制中起到举足轻重的作用，模型的精确度越精确，优化控制质量就越高。:实际过程中，由于系统工作域的迁移，使得离线数据样本所建立的模型并不能准确描述系统的实际状况.为了使模型能够准确反应系统的当前状态，应不断利用所获得的最新数据建立能够反映系统当前状况的新模型.即采用在线建模的方法。

1 LS-SVM在线建模递推算法

在LS-SVM中，用

来表示对象的模型，α和b是待定参数，求解方法是根据结构风险最小化原则，并使样本拟合误差最小化，把约束优化问题变成无约束优化问题，建立Lagrange函数，根据KKT条件，可得到线性方程组:

其中γ为调整参数因子。

K(xi，xj)是满足Mercer条件的核函数，常用的是径向基函数。

通过训练数据集{(xi，yi)}Ni=1，求解方程(3)来确定参数α和b。

就在线建模而言，需要不间断的增添新的数据到训练集中去，模型才可以实时的得以校正来适应新的对象特性改变，所以训练数据会被增加。LSSVM需要计算矩阵Φ-1，该矩阵的维数与训练数据量相等，在线建模过程中，Φ维数必然随着训练数据的增加而增长，矩阵求逆计算量非常大，所以不适用于在线建模［1］。

为了LS-SVM应用于在线建模，可采用一种递推最小二乘支持向量机回归算法:当训练数据增加时，可采用上次计算得到的参数递推得加入新数据后的参数，可以减少矩阵求逆计算［2］。具体算法如下:

假设数据集大小为N时得到的模型参考矩阵为ΘN=［b α］T，令PN=Φ-1N，当一个新的数据点{xN+1，yN+1}加入到数据集时

递推LS-SVM算法避免了大矩阵求逆，节省了计算时间［3］。但模型参数维数是随着训练数据线性增长，同时要保存所有的训练数据和Φ-1N。对于连续运行的对象，在线建模要进行下去，关键的问题是解决数据集规模的问题［4］。

经过一定量的递推计算后，训练后的模型达到较高的精度后，建模过程应保持训练数据集大小不变。即如果一个新的数据点加入到数据集，则同时删除原数据集中的一个数据，数据集总量保持不变。数据集中对于建模的重要程度可通过Lagrange乘子绝度值的大小|αi|反映出来，|αi|越小，对建模越无关紧要。因此在每次迭代过程中，把具有最小|αi|的数据点删除［5］。具体算法如下:

假定当前的数据集为{(xi，yi)}Ni=1，令

当数据集中最后一组数据{xN+1，yN+1}被删除时，

其算法实际是增加数据点推算法的逆过程［6］。

2 在线LS-SVMM建模的方法

(1)选取恰当的核函数与相应的参数，确定输入阶数nu和输出阶数ny与采样周期T0以及训练数据集的最大维数Nmax，还有性能指标中的参数γ和核函数的参数。

(2)对系统施加输入u，采样Nmax组输入输出数据{yk，xk}Nmaxk=1，构造初始的回归向量xk(k=1，2，…，Nmax)，形成初始训练集{yk，xk}Nmaxk=1，根据式(2)和式(3)分别计算得出模型的参数值PNmax与ΘNmax。

(3)新采样时刻k+1采样输入输出数据{yk+1，uk+1}构造新的回归向量xk+1得到新的训练数据。

(4)把PNmax和核函数代入式(6)～式(8)计算ψN+1，ζN+1和 ηN+1，根据式(4)、式(5)计算新的ΘN+1和PN+1。

(5)从上次运算获得的Lagrange乘子里找出最小|αi|相对应的序数I，在α中删除αi在数据集里删除(yi，xi)，设P11是矩阵PN+1除掉p11以后的方阵，P12是矩阵PN+1第I列除掉p11后列向量，P21是矩阵PN+1第I行除掉p11后的行向量，P22=p11，根据式(10)、式(11)计算Φ-1N，确定当前模型。转步骤(3)。

为检验在线建模与离线建模模型的精确性，以简单的非线性函数y=x sin(3πx)，x∈［1，10］作为建模对象，随机取该函数的400组数据。对于离线建模取其中200组数据作为训练数据，最后100组数据作为测试数据。在线建模采用300组数据作为训练数据，按照上述方法保持向量机的维数200不变，用相同的100组数作为测试数据。两种模型预测误差如下图1所示。表明在线模型能更好的预测输出，其精度大于离线模型，这种算法是有效的。

图1 预测误差

3 基于在线LS-SVM模型的广义预测控制仿真

预测控制源于工业实践，并在实践中发展和完善起来的一类计算机控制算法，具有鲜明的特征，是一种基于预测模型、滚动优化并结合反馈校正的优化控制算法［7］，其基本结构如图2所示。

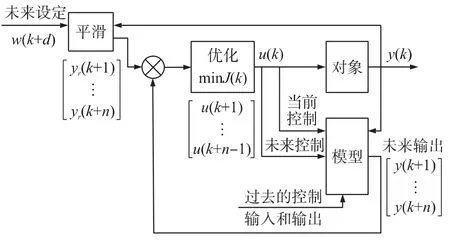
图2 预测控制的基本结构

预测控制中作为基础的预测模型，是对象动态特性的粗略描述，实际中不可能获得精确的数学模型，因为实际系统存在的非线性、时变、模型适配和干扰等不确定因素，基于不变模型的预测不可能准确地与实际情况完全符合，这就需要对基础模型进行在线修正。本文利用LS-SVM在线建模作为预测模型，提高预测模型的精度。

假设被控对象的CARMA模型为:

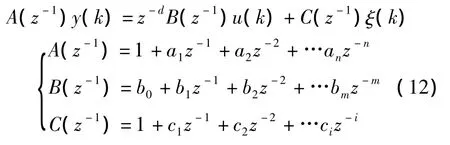
式中y(k)、u(k)和ξ(k)分别表示输出、控制量和白噪声，d为纯延时，n=2，m=5，i=1，其他各个参数未知。采用广义预测控制自适应算法，利用 LSSVM在线建模作为预测模型。训练数据集最大维数为200，核函数采用径向基函数，参数σ=1.77，γ =5，控制参数N=8，控制加权矩阵为单位阵I5×5，输出柔化系数α=0.7;期望输出ω(k)为幅值为10的方波信号，仿真结果如图3所示。

从图3我们能够看出，基于在线LS-SVM模型的预测控制，系统能够准确、快速地跟踪期望输出。

4 结论

LS-SVM模型参数的递推计算方法，可以使当前时刻的模型非常快地按照上一时刻的结果计算获得，可以应用到工业对象的在线建模。然而因为新的信息连续不断加入到训练数据集，这样就使在线模型的精确性比离线算法高。将其运用至广义预测控制里可以解决其中的非线性建模问题和提高控制质量。

图3 在线建模预测控制效果

［1］刘毅，王海清，李平.局部最小二乘支持向量机回归在线建模方法及其在间歇过程的应用［J］.化工学报，2007，11:2846 -2851.

［2］张浩然，汪晓东.回归最小二乘支持向量机的增量和在线学习算法［J］.计算机学报，2006，29:400-406.

［3］Goethals I，Pelckmans K，Suykens JA.Identification ofmimohammersteinmodels using least squares support vectormachine［J］.Automatica，2005，41:1263-1272.

［4］Ke Y，Yiyu C.Discriminating the Genuinenessof Chinese Medicines Using Least Surares Support Vector Machines［J］.Chinese Uournal of Analytical Chemistry，2006，34(4):561-564.

［5］Comak E，Polat K，Gunes S.A New Medical Decision Making System:Least Square Support Vector Machine(LSSVM)with Fuzzy Weighting Preprocessing［J］.Expert Systems with Applications，2007，32:409-414.

［6］张英，苏宏业.基于模糊最小二乘支持向量机的软测量建模［J］.控制与决策，2005，20(6):621-624.

［7］庞中华，金元郁.基于误差校正的预测控制算法［J］.化工自动化及仪表，2005，32(2):1-4.

Application of LS-SVM On-Line M odeling in Predictive Control*

Hong Zhou*
(Department of Information Technology，Guangzhou City Polytechnic，Guangzhou 510405，China)

Aiming at the predictionmodel in intelligent predictive control，the recursive algorithm of LS-SVM on-line modeling was put forward.which reducing the calculation of inversematrix.After the onlinemodel achieved to high accuracy，it removed with the smallest|αi|data pointwhen a new data pointare added to the data set in each iteration process，Itwas not only solved the problem of the size of the data set but also improved the accuracy of prediction model.The simulate result shows that the predictive control based on LS-SVM on-linemodeling could tracking the expected output rapidly and stably，and achieving anticipated control effect.

LS-SVM;on-linemodeling;predictive control;prediction model

10.3969/j.issn.1005-9490.2014.01.037

TP18 文献标识码:A 文章编号:1005-9490(2014)01-0154-03

项目来源:广东省哲学社会科学“十二五”规划项目(GD11YJY01);广州市教育局资助广州市教育科学“十二五”规划项目(11B016)

2013-04-21修改日期:2013-05-22

EEACC:7210

洪 洲(1979-)，男，汉族，江西东乡人，硕士，副教授，主要研究方向为A-gent软件技术、计算虚拟化、人工智能。