一种利用多主体领域系统进行数据聚类的新方法*
刘永立
(北京财贸职业学院信息物流系,北京101101)
一种利用多主体领域系统进行数据聚类的新方法*
刘永立*
(北京财贸职业学院信息物流系,北京101101)
提出一种数据聚类方法:MATS,该方法受蚁群算法启发,同时应用存在性技术,例如密度概念和聚类有效性指数(DB -指数)。MATS可以自动根据一些与数据集不直接相关的参数找到簇。实验结果证明了MATS可以识别不规则簇并能有效应用于图像分割,在图像分割速度和效果方面比传统聚类算法(如FCM算法)有明显提高。
数据挖掘;多主体领域系统;数据聚类;图像分割
数据聚类是按照某种相似性度量,将具有相似特征的样本归为一类,使得类内差异相似度较小,类间差异较大。但目前为止,还没有任何一种聚类技术(聚类算法)可以普遍适用于揭示不同的数据集结构,一般来说,不同的聚类技术应用于不同场合和领域。
数据聚类在很多领域都有应用。其中,在模式识别及图像分割领域近年来有很多新的研究成果。Pwitt首先提出了图像分割时应该采用模糊处理的方法[1]。同时训练样本图像的匮乏又需要无监督分析,而模糊聚类正好满足这两方面的要求,因此模糊聚类分析成为图像分割中一个强大的研究分析工具[2]。
在实际中,应用最广泛当属Bezkek于1981年提出的模糊C-均值算法FCM(Fuzzy C-Means),此算法在本质上是一种多次迭代局部寻优的过程,其结果在很大程度上依赖于初始值的设定,很容易陷入局部最优值。为解决此缺点,许多学者通过借鉴智能算法的全局寻优、收敛速度快的优点,将其与FCM结合在一起,可以得到许多基于智能计算的模糊聚类图像分割算法。诸如文献[3-4]中提到的结合蚁群算法、文献[5]中提到的结合遗传算法、文献[6-7]中提到结合粒子群算法,这些算法都对用于图像分割的模糊聚类算法进行了一定程度的改进和优化。但是,由于这些智能算法自身的特点,造成算法搜索时间较长,收敛速度较慢,并且数据集较大时容易出现早熟现象。
因此,在本文中提出一种新的数据聚类方法:多主体领域系统(以下简称MATS),这种方法是受蚁群优化算法的启发,同时应用了一些存在性技术,如:密度概念[8]和聚类有效性指数(DB-指数)[9]。该算法根据一些与数据集不直接相关的参数找到簇,能有效用于图像分割。实验仿真结果证明了该算法的有效性,并通过与FCM算法、AAFCM算法进行比较,显示出该方法在图像分割的速度和效果方面较传统算法有显著提高。
1 数据聚类与MATS
聚类是一种常用的非监督式分类技术,它基于相似性或相异性将输入空间划分到K区域中。分区或簇的数量事先可能知道,也可能不知道。输入空间S由n个对象表示{X1,X2,…,Xn},簇(主体)由C1,C2,…,Ck表示。其中Ci(i=1,2,…K)需要满足如下条件:
(1)Ci≠φ i=1,2,…,K
(2)Ci∩Cj=φ i,j=1,2,…,K,and i≠j
(3)C1∪C2∪C3∪…∪CK=S
若根据数据在聚类中的积聚规则以及应用这些规则的方法,可以将聚类算法分为传统聚类算法和聚类新算法。在传统聚类算法中,包括基于划分的聚类、基于层次的聚类、基于密度的聚类等多种算法;在聚类新算法中,包括模糊聚类、基于流增量的聚类、基于生物智能的聚类等多种聚类算法。
本文提出了一种新的聚类算法:多主体领域系统(MATS),该方法受蚁群优化算法的启发,一方面借鉴了模糊聚类的思想,另一方面利用传统聚类算法中的密度概念以及聚类有效性参数——DB-参数来解决聚类问题。具体来说,该算法分为如下两步。
步骤1:首先在随机位点(对象)上初始化K主体,并使用靶向步骤来搜索入侵的对象。而协调步骤则用于解决争夺同一对象的主体之间的冲突,因为一个对象只能属于一个主体。然后使用入侵步骤来帮助主体占据靶向对象。最后,系统将没有对象的主体清除掉。步骤1将一直重复直到所有对象都被占据。
步骤2:系统首先利用所有现有的主体来计算半径r以满足领域规则;然后使用聚类有效性参数——DB-参数找寻到符合领域规则的簇对;最后,使用密度概念在主体之间建立起领域策略,并组合或调整主体。步骤2将一直重复直到无法再建立更深层的领域策略。
2 MATS算法描述
2.1 靶向功能
假设输入空间S由n个对象{X1,X2,…,Xn}表示,Ok是属于主体k的对象集。因此,本文可以将S分为对象集Ok和Fk,其中Fk是不属于主体k的对象集。当主体k搜寻入侵对象时,它将随机选择从它在Ok的位点中选择对象i,并根据与Fk的欧几里得距离用对象i找到候选对象集Rk。最后,主体将从Rk中随机选择一个对象t。
必须要注意的是,对象t必须是对象i的近邻对象,从而使得主体k的散度最小化。换句话说就是,t∈nb(i),其中nb(i)是对象i的近邻对象。因此,需要进行预处理来找寻每个对象的近邻对象r。但是当聚类数据库较大时这必将影响MATS的效率。为解决这个问题,本文使用局部框架方法来有效进行预处理。局部框架方法意味着我们能在边长为L的正方形中找寻到对象i的近邻对象r。
2.2 协调步骤
在此方法中,主体是平行的竞争者,因此争夺同一对象的主体之间会发生冲突。为解决此问题,该系统使用决定条件来协调主体。在决定条件中的优先次序如下:(1)距离:决定哪个主体和对象最为接近;(2)对象数量:决定哪个主体占据最多的对象; (3)分散程度:决定哪个主体有更为紧凑的对象。
2.3 入侵步骤
当主体k能占据对象t时,可以用式(1)来计算气味λ(k,t),即主体k在对象t上存留的气味量。在式(1)中,d(k,t)是对象t和主体k位置之间的距离。此外,主体k必须考虑到对象t的状态。如果对象t未被占据,主体t可以直接占据。如果对象t已被主体k'所占据,则主体k要和主体k'比较二者之间的气味。
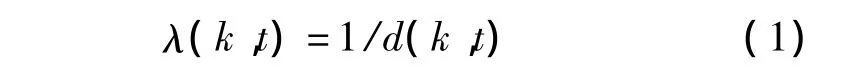
2.4 计算半径
为防止主体重复性争夺同一对象导致步骤1中无止境的竞争,可以使用密度概念来建立领域原则。当步骤1完成后,输入空间D中所有的对象都由主体k划分为k候选簇。由于主体随机划分领域,一个簇可能包含多于一个候选簇。因此如果候选簇属于同一个簇的话,有必要找到一个原则来连接这些候选簇[10]。
Tao CW提出了一个有效的标准:使用密度概念来找出候选簇之间的关联度[11]。因此半径值对于找寻到对象的邻域非常必要。
半径值会影响对象的邻域和散度,因此每个维度数据点的散度都是一个重要的因素[12]。例如,如果数据点的散度很大,而其邻域很小,则可能在任何一个数据点的邻域中都不存在数据点。另一方面,如果散度很小,而其邻域很大,则整个数据集可能落在所有数据点的邻域中。根据Tao CW的论点,通过选取散度不同的候选簇的不同半径值,可以合理地解决该问题[13]。尽管可以用标准偏差大概地表示半径,但本文还是使用了数据点的散度来表示半径。半径值r的定义参见下面式(2)和式(3)。

这里I∈K。
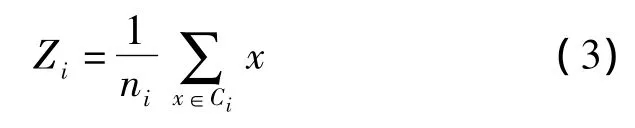
当Ci是候选簇i时,Zi是Ci的中心,如式(3)中的定义。其中ni是Ci中包含的对象数量。
2.5 应用DB-参数
DB-参数是由Davies D L和Bouldin D W在1979年提出的一种聚类有效性参数[14]。该参数是簇内散度和簇间距比例的函数,见式(5),其中dij是候选簇i和j中心之间的欧几里得距离,见式(4)中的定义。ri和rj由式(2)计算出来,式(2)用于计算候选簇i(Ci)内的散度。其中Zi是Ci的中心,并在式(3)中进行定义。此外,ni是Ci中的对象数量。

2.6 领域策略
领域策略用于评估簇对的关系。在MATS中有两种领域策略。一种是完全关联策略,另一种是部分关联策略。完全关联策略表示簇对之间的关联度很高,因此它们之间是关联的。换句话说,这些簇对应该属于一个簇。部分关联策略则意味着簇对之间的关联度中等,因此它们彼此之间可以交换对象。换句话说,一个簇对含有属于另一个簇对的对象,而且这两对簇可以互相交换对象。
在MATS中,完全关联策略首先在簇对(Ci,Cj)中进行检验,因为候选簇Ci和Cj如果完全关联的话不存在部分关联策略。首先计算出簇对(Ci,Cj)的半径值rij。见式(6):

随后,p2,p3,…,ps-1均匀分布在连接CCi和 CCj的线上。其中p1=CCi,ps=CCj,。CCi是候选簇Ci的中心,而候选簇Ci是Ci所有对象的中数。CCj是候选簇Cj的中心,而候选簇Cj是Cj所有对象的中数。|p2-p1|=|p3-p2|=…=|ps-ps-1|=|ps-p1|/(s+ 1)=rij/2以半径值rij为参数来计算pm的密度,密度函数见式(7)。

其中m是Ci和Cj之间的数据点,m=1,2,…,s。
hi是Ci的对象数
hj是Cj的对象数Xl是属于Ci或Cj的对象l。
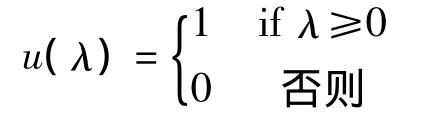
式(8)定义是由Tao CW提出的评估标准,用来评估簇对(Ci,Cj)之间是否存在完整关联。在式(8)中,α是一个很重要的参数,它可以影响聚类的结果。尽管Tao CW将α设置为4,但在MATS中通过一些测试被设置为17。

如果簇对(Ci,Cj)中不存在完全关联,那么将会核实簇对(Ci,Cj)中是否存在部分关联。起先,Ci的对象以半径值为ri分散在Ci(内部)和Ci(外部)中。换句话说,如果对象n属于Ci,而对象n和CCi的距离比半径值ri小的话,则对象n归类于Ci(内部)。反之,对象n归类于Ci(外部)。同理,Cj的对象分散在Cj(内部)和Cj(外部)中。
用于检测簇对(Ci,Cj)是否存在部分关联的标准在式(9)中进行了定义。在式(9)中,Wi是属于Ci(外部),但更接近于Cj的对象所组成的对象集。Wj是由属于Cj(外部),但更接近于Ci的对象所组成的对象集

3 实验仿真与结果
为了验证新方法的效果,我们将包含512×512个三维数据点的图片进行分级,以证实MATS在多媒体数据分割方面的有效性。
该数据集包含512×512个三维(RGB)数据点(262144)。为减少计算量,我们首先使用局部框架方法将邻域的数据点整合进L=10的对象中。经过局部框架方法处理后,对象数量为7623。然后我们用这些参数:k=40,r=150,L=255/20来运行MATS将这些对象进行聚类。同时为了与传统算法比较,从而验证MATS算法的可靠性和效率,采用MATLAB7.0仿真环境,对图(a)再次分别用FCM、基于蚁群算法的FCM(AAFCM)进行分割处理,FCM、AAFCM的初始参数m=3,单步最小变化为0.000 06,最大迭代次数90。整体分割效果如图1所示。
通过比对发现,若采用MATS算法,大概需要时间5 s完成步骤1。候选簇的数量为36,然后用这个候选簇来运行步骤2。步骤2的运行时间大概为10 s,并得到了13个簇;若采用FCM和AAFCM算法,相同设备上算法运行时间分别是53.6 s和47.2 s。从时间上面来看,MATS有明显提高。3种算法的迭代次数和收敛时间如表1所示。

图1 分割效果比对

表1 3种算法迭代次数及收敛时间比较
为了进一步评价不同算法对图片分割的差异性,对分割结果用如下评价指标:划分系数vpc、划分熵vpe、类间关联度vxp作进一步的定量分析。当聚类结果最优时,划分系数值vpc应该最大,划分熵值vpe应该最小,类间关联度值vxp应该最小。比较结果如表2所示,可见AAFCM和MATS分割效果要明显优于FCM算法,且MATS分割算法有效性评价指标比AAFCM有了较大提高。

表2 3种算法评价指标比对
从视觉观察3种分割结果,由于FCM聚类算法的局部收敛不足,明显看出FCM算法分割的边界模糊,尤其是在樱桃和柠檬的分割中,效果较差。AAFCM算法和MATS算法分割结果比较,在葡萄和柠檬的分割中差异不大,但在樱桃的分割中,由于MATS算法在步骤1中使用局部框架方法对数据进行了整合,并在步骤2中应用DB-参数和领域策略进行调整,使得分割结果保留了更多的细节信息。由此可见,MATS算法能克服传统算法对初始参数的依赖,并在一定程度上避免陷入局部极值。
4 结论
聚类是已知的一种探究数据分析工具,它将数据分类到不同的簇中。传统的聚类算法遇到很多难题,例如:(1)需要提前知道一些数据信息;(2)很难找到不规则簇;(3)聚类较大数据库时效率低下等。本文提出的多主体领域系统(MATS)是在传统聚类算法基础上借鉴了蚁群优化算法的思想,并进行了改进。该算法与FCM算法、AAFCM算法等传统算法相比,在图像分割速度和精度方面有一定程度的提高,并克服了传统算法依赖初始参数、容易陷入局部极值的缺点。
[1]孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008,19 (1):48-61.
[2]Xu Rui.Survey of Clustering Algorithm[J].IEEE Tran on Neural Networks,2005,16(3):645-678.
[3]李积英,党建武.量子蚁群模糊聚类算法在图像分割中的应用[J].光电工程,2013,40(1):126-131.
[4]杨立才,赵莉娜,吴晓晴.基于蚁群算法的模糊C均值聚类医学图像分割[J].山东大学学报(工学版),2007,6(3):51 -54.
[5]白杨.蚁群算法在磁共振图像分割中的应用[J].中国医学影像技术,2007,23(9):1402-1404.
[6]杨凯,蒋华伟.模糊C均值聚类图像分割的改进遗传算法研究[J].计算机工程与应用,2009,45(33):179-183.
[7]张利彪.基于粒子群优化算法的模糊C均值聚类[J].吉林大学学报,2006,44(2):217-221.
[8]陈治亚.一种基于微粒群的模糊聚类算法[J].计算机工程,2007,33(2):198-199.
[9]周涛,陆惠玲.数据挖掘中聚类算法研究进展[J].计算机工程与应用,2012,48(12):102.
[10]杨海波,华惊宇,刘半藤.基于减聚类优化算法的无线传感网络分簇路由协议研究[J].传感技术学报,2012,25(11):1603-1606.
[11]李成法,陈贵海,叶懋,等.一种基于非均匀分簇的无线传感器网络路由协议[J].计算机学报,2007,30(1):27-36.
[12]赵福星,吕玉泽,郑小梅,等.基于固定任务混频的寿命相关载荷分布特性[J].航空动力学报,2013,28(1):32-37.
[13]吴振华,尹志军.基于优化簇半径的WSNs非均匀分簇路由[J].计算机工程与设计,2010,31(15):3374-3378.
[14]曹永春,邵亚斌,田双亮,等.一种基于分组遗传算法的聚类新方法[J].西华大学学报,2013,32(1):39-43.
A NEW Data Clustering Using M ulti-Agent Turf System*
LIU Yongli*
(Beijing Vocational Collegeof Financeand Commerce,Beijing 101101,China)
A new data clusteringmethod MATSwas proposed,which was inspired by Ant Colony Algorithm,In addition,there are some existence techniquewas also utilized in ourmethod,such as the density conceptand cluster validity index(DB-index).MATS can automatically find clusters,depending on a few parameters that are not directly related to the data set.The experiment results verified thatMATS is able to discover clusterwith varying shapes and it is effective when applied to image segmentation.
datamining;multi-agent turf system;data clustering;image segmentation
10.3969/j.issn.1005-9490.2014.01.036
TP311.13 文献标识码:A 文章编号:1005-9490(2014)01-0150-04
项目来源:国家自然科学基金项目(61272350)
2013-04-18修改日期:2013-06-23
EEACC:7210G
刘永立(1970-),男,汉族,河北涿州市人,北京财贸职业学院讲师,北京邮电大学软件工程硕士,研究方向为模式识别、人工智能WEB软件开发,cgyliu @126.com。


