钻铤坠物冲击下的平台甲板塑性失效分析

王 醍 张延昌 任慧龙 荆海东 林 瞳

（1.哈尔滨工程大学 船舶工程学院 哈尔滨 150001；2.中国船舶及海洋工程设计研究院 上海 200011）

引 言

近年来，海洋平台事故发生频繁，尤其是坠物事件占海洋平台事故总数的34.8%，在海洋平台事故中位列首位［1］。据统计，坠物主要有方圆体和细长体两种形式［2］，钻铤则是细长体坠物的典型代表。该种坠物拥有细长的外形，并且接触面刚度很大而接触面积较小，因此在较小的动能下就能对甲板面造成破坏，而且很容易穿透甲板，对甲板下方结构造成威胁。所以，研究钻铤坠物冲击下甲板的塑性失效问题尤为重要。

大部分船级社都没有关于坠物事件的规范要求，只有DNV和BV船级社对坠物问题提出较为详细的规定。DNV规范中指出坠物事件只会发生在坠物可能坠落的区域内，坠物事件属于意外事件，在碰撞过程中坠物冲击的能量将被消耗，并需对被撞击结构的结构响应进行评估。坠物载荷是由受坠物质量和冲击速度影响的坠物动能所确定的，大多数情况下坠物动能主要会转化为被撞击部分的变形能，也可能转化为坠物本身的变形能，但对于管状坠物轴向撞击或质量很大的物体撞击时，一般将坠物等效为刚体，因此本文中用刚体材料对钻铤坠物进行模拟。另外，规范还指出，坠物问题应考虑坠物以一定角度撞击，如果被撞击结构是自由浮动的结构物，坠物撞击角度应与垂直方向偏移10°，若为底部受支撑的结构则为5°。［3］BV船级社的标准则更为严格，规范要求坠物事件的安全标准为被撞击物能承受一定程度的永久变形，并且结构不会发生破裂。两种规范中都指出可采用考虑材料弹塑性的非线性有限元软件对坠物问题进行计算分析，因此本文采用在碰撞问题中广泛应用的非线性有限元软件MSC/DYTRAN进行计算分析。［4］

Arne Wenger在1983年针对钻铤坠物进行了一系列的全尺度模型试验，他将钻铤坠物分别从8～42 m的高度坠落在板厚分别为0.012～0.047 m的板架上，并测得了板架的变形能［5］。Y. F. AL-Obaid利用FORTRAN77根据经验公式研发出一套针对于不同材料参数和下落高度计算贯入和穿透金属物体问题的程序，并提供部分源程序供他人研究和借鉴［6］。郝瀛针对箱型坠物利用数值仿真方法研究甲板结构破损的临界变形能，针对不同网格尺寸及坠落位置，得出临界变形能的加权系数，从而得到板架整体的临界变形能，为实际工程问题提供了一定的指导依据。

本文对具体工程问题进行合理简化，确定合适的载荷及边界条件，讨论不同碰撞条件对结果的影响，并对计算结果进行分析及归纳［7-11］，提出指导工程实际问题的经验公式。

1 有限元数值仿真技术

为了对有限元数值仿真方法进行探究，本文借鉴文献［5］中的实验工况进行数值仿真模拟并将计算结果与实验结果进行对比，以验证数值仿真分析技术的可靠性及精度。

1.1 有限元模型及相关参数

参照文献［5］中实验工况，将重约3172.8 kg的钻铤坠物从18.1 m高度处垂直坠落在厚度为0.02 m的四周刚性固定的平板上。根据动能守恒定律，坠物冲击平板的速度为v=18.84 m/s，钻铤坠物尺寸详见图1，板架尺寸为12.2 m×7.3 m。板架材料为AH36高强度钢。参照上述参数进行有限元建模，对碰撞区域网格进行适当的细化，细化后网格尺寸为0.08 m×0.09 m，有限元整体模型如图2所示。

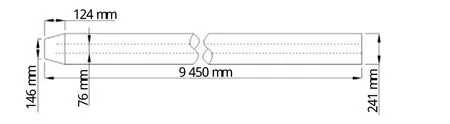
图1 钻铤结构图

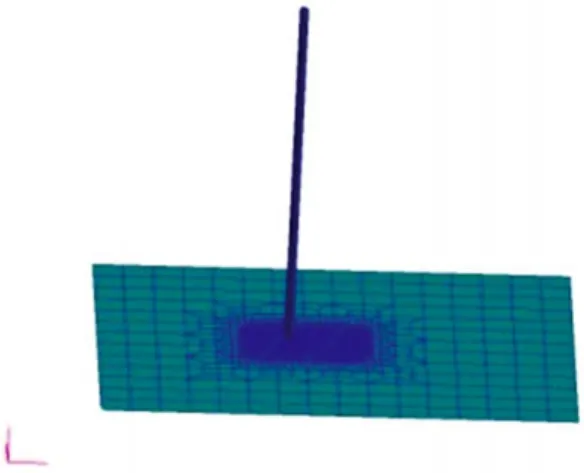
图2 简化结构模型图

板架材料选取DYMAT24这种非线性塑性材料，材料密度为7850 kg/m3，弹性模量2.06×1011Pa，泊松比为0.3，屈服应力为3.55×108Pa，应变硬化模量为1.18×109N/m2，最大塑性应变为0.1，应变率敏感系数D和p分别取40.4和5。可将钻铤坠物材料等效为刚体。接触方式选择主从面接触及自适应接触两种形式。其中主从面接触设置钻头碰撞处为主面，板架被碰撞处为从面。设置静摩擦系数为0.2，动摩擦系数为0.1。

1.2 计算结果分析

利用MSC/DYTRAN对结果进行分析计算。对结果观察可知，碰撞发生后，甲板面迅速被破坏并穿透，但周围结构并没有发生很大的变形。碰撞结束后，物体仍具有很大的动能继续向下运动，甲板板架吸收了总能量30%左右的变形能，碰撞力变化曲线如图3所示。碰撞过程中坠物动能Ek.o、板架变形能Es.p以及板架动能Ek.p的变化情况如图4所示。

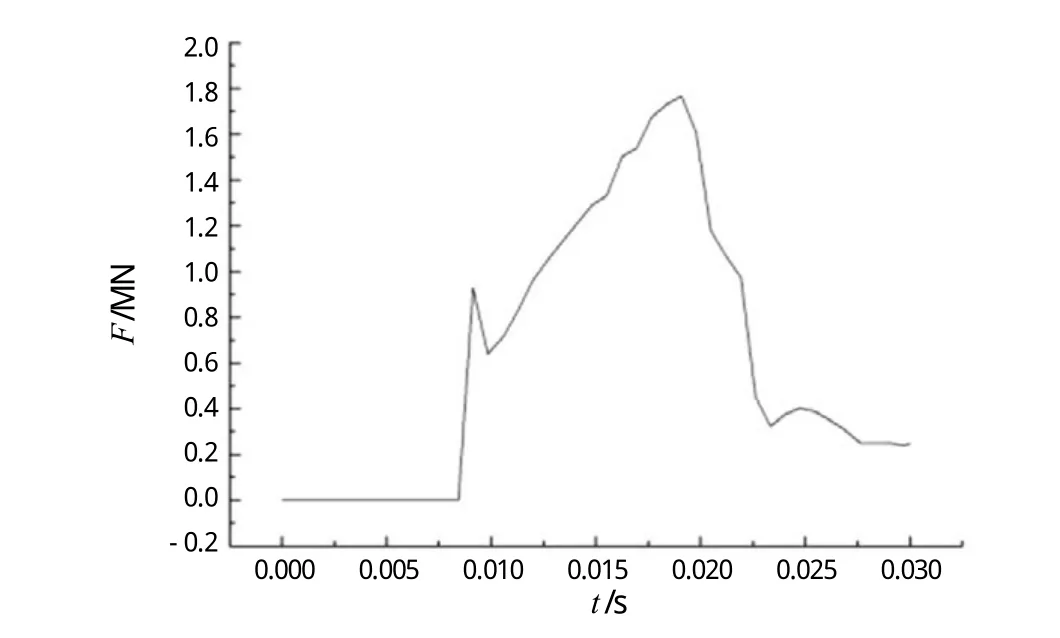
图3 碰撞力-时间历程曲线

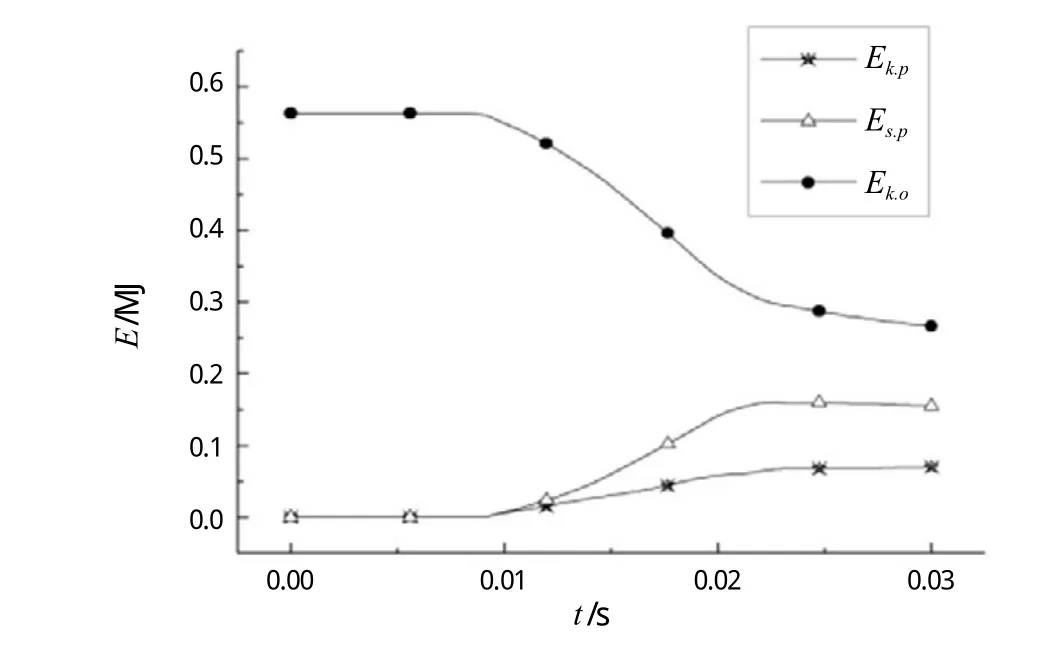
图4 能量-时间历程曲线

计算得到的板架变形能Es.p= 0.181 MJ，借鉴文献［5］中的全尺度模型试验结果，板厚b = 0.02 m的工况试验测得的板架总变形能Es.p= 0.192 MJ，有限元软件计算结果与实验结果数据基本吻合。由此可见，此种方法下数值仿真结果真实可信，参数设置基本合理，可以一定程度上指导工程实践问题。

2 坠物载荷作用下的某平台甲板塑性失效分析

根据DNV规范规定，坠物问题研究区域应为坠物可能坠落区域［3］，因此选取吊机工作范围内下的一块甲板板架作为简化的平台甲板模型来研究坠物问题以提高计算效率，具体尺寸见图5。

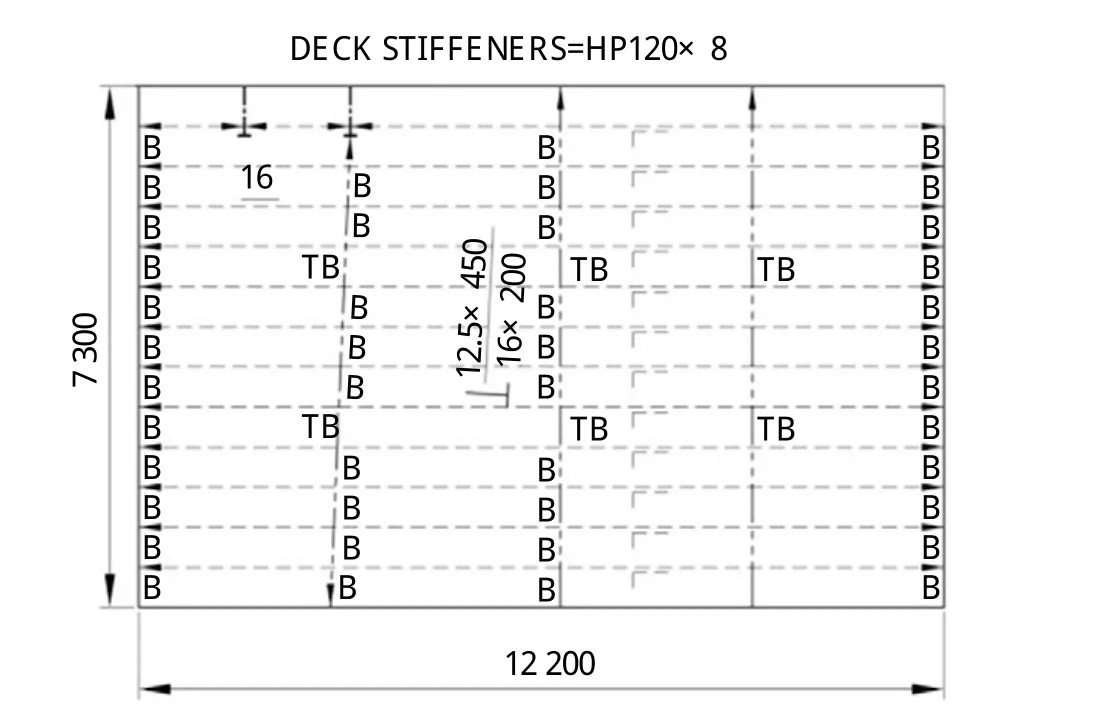
图5 甲板板架图

DNV规范中给出钻铤坠物撞击海平面的速度通常约为24～26 m/s，根据能量守恒定律反推，可知下落高度距水平面30 m左右，而本文要研究的是钻铤坠物撞击平台甲板面的情况，应减去平台甲板面至水平面的距离，可知钻铤坠物大约应从距甲板面10 m左右处坠落，撞击甲板面的速度v=14.01 m/s。除板架尺寸不同外，其他碰撞参数同本文第一部分数值仿真分析中设置相同，下面对碰撞结果进行分析。

2.1 甲板板架变形情况

碰撞前坠物距平台甲板面距离为0.1 m，t = 0.0071 s时坠物开始接触甲板面，平台甲板面以碰撞点为中心开始产生圆形的凹陷状塑性变形，如下页图6所示。t = 0.0298 s后甲板面开始产生破裂，甲板面产生破裂后破裂面积迅速扩大，直到t = 0.0310 s时钻铤能顺利通过，此后，平台甲板面将不会继续破裂，直到碰撞结束。平台甲板面破裂情况如图7所示。

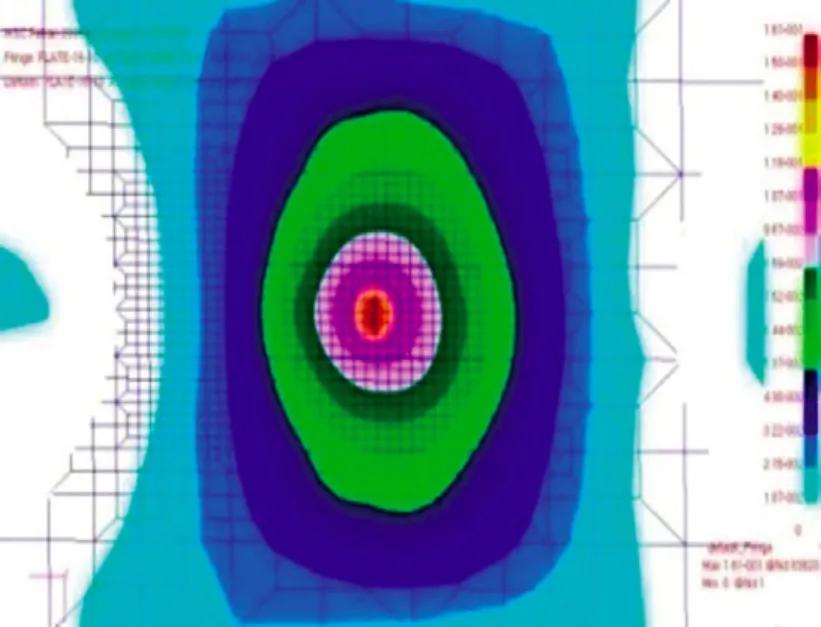
图6 破裂前的甲板板架位移云图（t=0.0298 s）

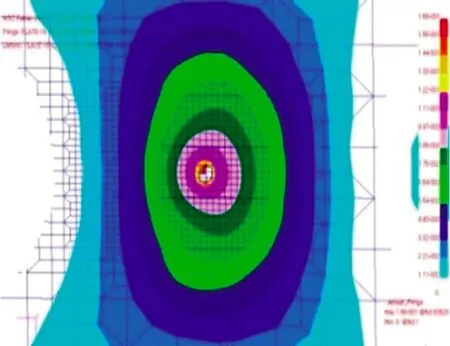
图7 破裂后的甲板板架位移云图（t=0.0310 s）

2.2 能量变化情况

坠物撞击平台甲板后，除碰撞过程中损失的能量外，坠物动能大部分转化为平台甲板由于塑性变形产生的变形能，小部分能量转化为甲板板架的动能，使甲板板架产生局部的震动。系统内各能量变化曲线如图8所示。钻铤坠物将甲板面穿透后继续向下运动，此时坠物仍保留30%左右的动能。经计算，坠物撞击的初始动能越大，碰撞结束后坠物保留的动能占初始动能的比例越大。

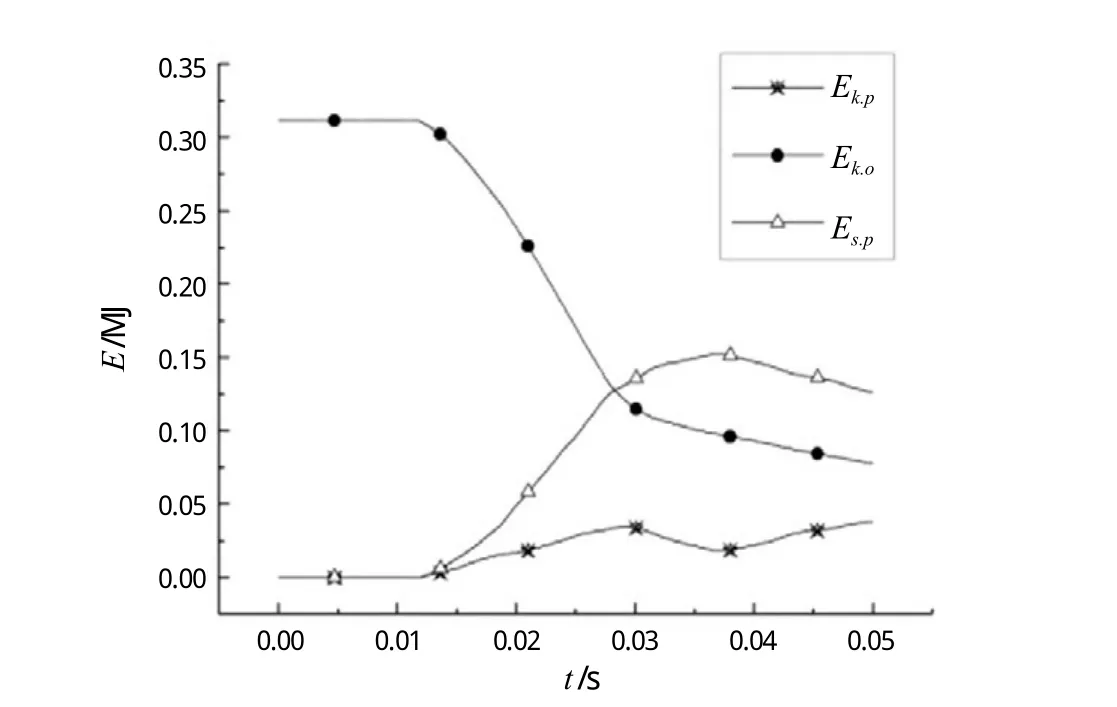
图8 能量-时间历程曲线

2.3 碰撞力变化情况

碰撞力变化曲线如图9所示。在t = 0.012 s开始有碰撞力产生， t = 0.029 s后碰撞力达到峰值，最大碰撞力F = 1.44 MN。此时的甲板面开始破裂，碰撞力随之迅速回落，t = 0.031 s后坠物完全穿透甲板面。由于坠物与破口边缘的摩擦作用较小，因此，碰撞力曲线开始在较低的范围内成波动趋势。

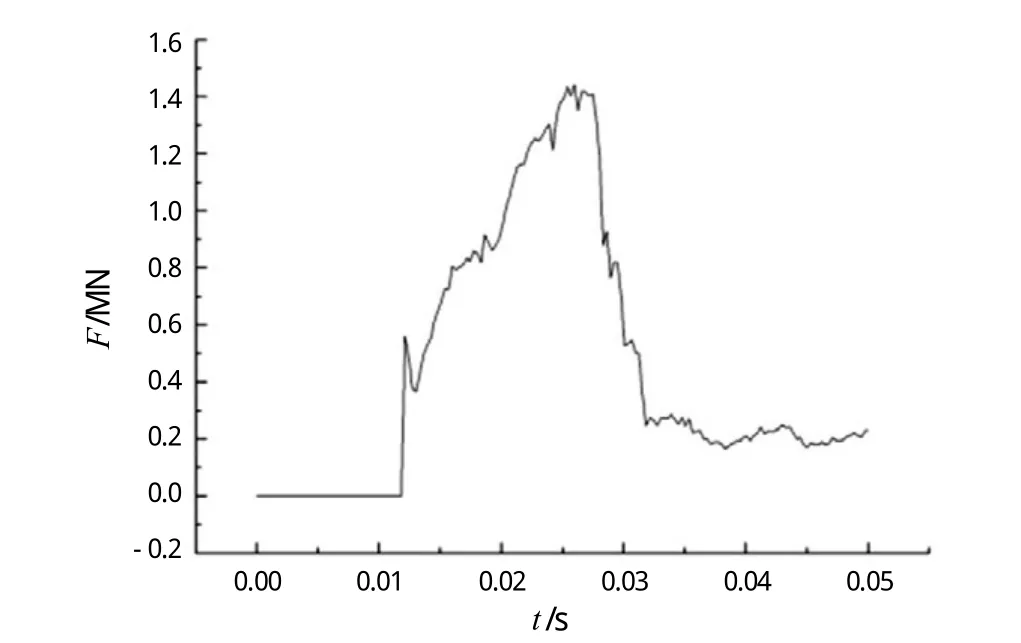
图9 碰撞力-时间历程曲线

3 碰撞参数分析

坠物事件属于偶然意外事件，具有很大的随机性，存在着多种碰撞的可能性。为了更深入研究坠物载荷作用下甲板的塑性失效问题，本文将对多种碰撞条件进行模拟，分析不同碰撞条件下的不同碰撞结果。

3.1 撞击位置对结果的影响

为了研究坠物撞击在不同位置的结构响应，分三种情况进行研究:撞击点在甲板板上、撞击点在纵骨上、撞击点在横梁上。板架尺寸保持不变，碰撞参数与本文第1.1节中的设置相同。

（1）塑性变形

在该冲击动能下，撞击点在甲板板上和纵骨上时，坠物都会对甲板面造成破坏并穿透，并且撞击点在纵骨上时，甲板板架骨材首先发生破裂，继而甲板面被全部穿透。而撞击点在横梁上时，甲板的板架只是产生很大的塑性变形，但并未破裂，而且坠物还会发生反弹。如果板架被撞击处并非关于坠物碰撞点中心对称，则坠物会伴随着旋转运动以一定角度反弹，且与竖直方向角度越来越大，直到坠物平躺在平台甲板上，碰撞结束后，甲板面留下一个局部凹陷状的塑性变形。

（2）能量吸收

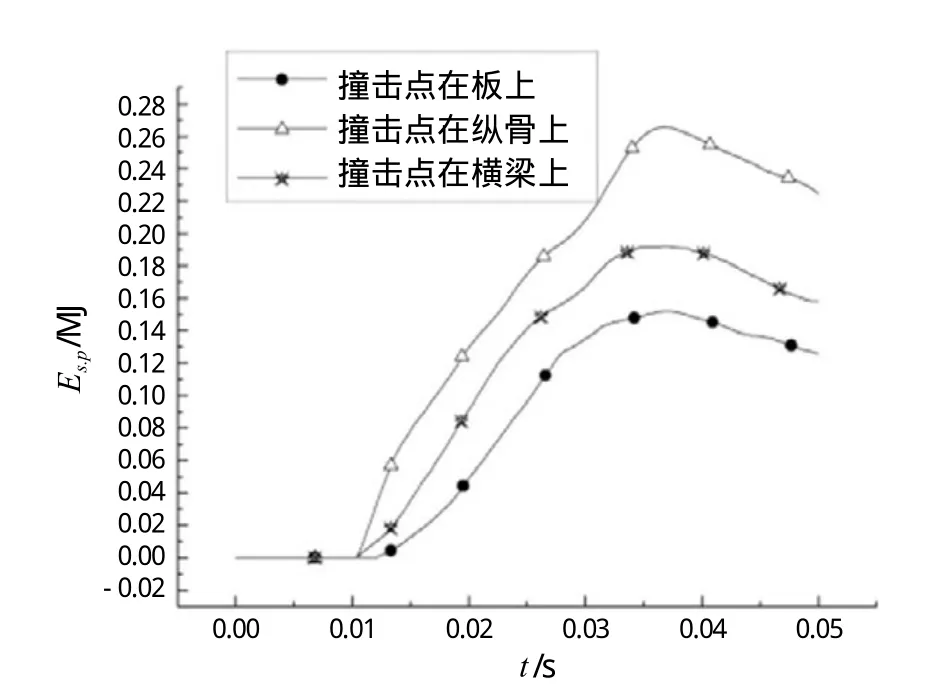
图10 板架变形能-时间历程曲线

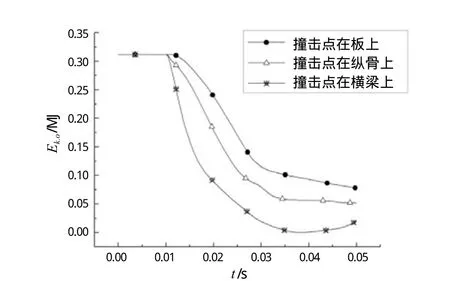
图11 坠物动能-时间历程曲线

三种情况下的板架变形能Es.p和坠物动能Ek.o变化情况如图10、图11所示。撞击点在横梁上时，板架产生的变形能最大，坠物动能会回落为0。当t约为 0.04 s时，一部分的板架变形能重新转化为坠物动能， 坠物会发生轻微的反弹运动。不过，另外两种情况则不会发生此种状况，坠物穿过甲板一定距离后，动能被完全消耗，在自身重力作用下继续下落，直到再次碰到其他物体使运动停止。撞击点在甲板板上时，坠物消耗的动能最少，故对甲板下方结构的威胁最大。

（3）碰撞力

不同撞击点时碰撞过程中的碰撞力曲线如图12所示。撞击点在横梁上时，撞击力会瞬间迅速增大，最大碰撞力几乎是另外两种情况的一倍，说明此时坠物与板架间的相互作用最大，继而也以很快的速度回落，并且相对于其他两种情况来说，冲击结束后碰撞力仍在一个较高的水平上波动。撞击点在纵骨上要比撞击点在甲板板上时碰撞力大，并且撞击点在甲板板上时，碰撞持续时间最短，坠物最容易穿透甲板面。

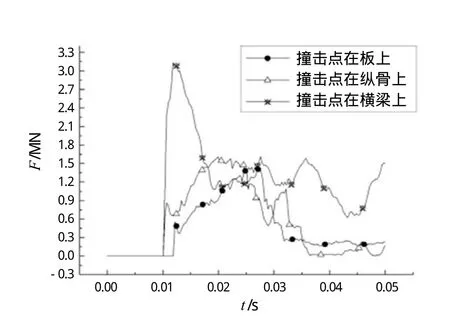
图12 撞击力-时间历程曲线

综上分析，坠物以相同动能冲击甲板板架时，撞击点下方板架支撑构件越强，碰撞过程中碰撞力越大，板架吸收的变形能越大，坠物消耗的动能也越多，并且坠物可能出现反弹运动，最终坠物将平躺在甲板面上。若坠物穿透甲板面，甲板下方骨材首先产生塑性失效并破裂，继而甲板面发生破裂。

3.2 撞击角度对结果的影响

由于海洋平台的作业环境一般比较恶劣，并且海上风力也比陆地上大得多，因此坠物在下落过程中常常带有一定角度撞击平台甲板平面。为了研究不同角度对结果的影响，将坠物设置成与甲板面垂直方向夹角α = 5°和α =10°时对甲板面进行冲击，其他碰撞参数同本文第1.1节中设置相同。

（1）塑性变形

通过对t = 0.5 s时甲板板架的变形情况观察可知，坠物以不同角度撞击平台甲板时，甲板面破裂情况基本相同，只有坠物穿透区域发生局部破坏，其他部位变形很小。坠物撞击甲板的同时还伴随一定的旋转和向一侧倾倒运动，并且α越大，坠物在撞击过程中向一方倾倒的程度越剧烈，但是旋转的角度越小。三种角度撞击下，钻铤坠物的位移曲线如图13所示。可见，相同时间条件下，当坠物以α = 5°角度撞击甲板时，穿透甲板后的位移最大且对甲板下方结构威胁也最大。

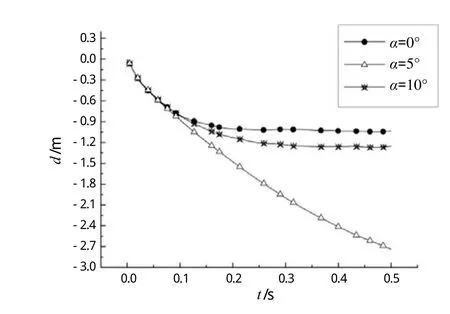
图13 坠物位移-时间历程曲线

（2）能量吸收

不同角度撞击下甲板板架的变形能变化曲线如图14所示。当坠物以一定角度撞击甲板面时，碰撞结束后板架变形能变化情况要比垂直撞击更剧烈，α = 5°撞击时甲板板架变形能最大。

图14 板架变形能-时间历程曲线

坠物动能变化曲线如图15所示。α = 5°撞击时，坠物动能消耗最少，碰撞后相同时间时坠物动能最大。

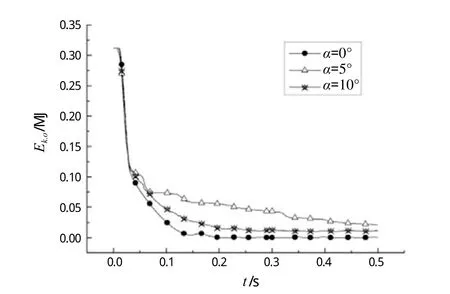
图15 坠物动能-时历变化曲线

板架动能变化曲线如下页图16所示。α = 5°撞击时，板架动能变化最剧烈。由于碰撞过程中坠物动能主要转化为板架的动能、板架变形能和坠物穿透甲板面后的坠物动能，而在系统初始总能量相同的情况下，碰撞结束后，α = 5°撞击时坠物动能、板架动能和板架变形能均大于另外两种情况。

图16 板架动能-时间历程曲线

因此考察系统内能量耗散情况，对0.5 s时系统内能量进行统计得到系统内能量耗散情况（见表1）。可见，α = 5°撞击时的系统能耗最小，耗散的能量主要包括系统沙漏能、板架的弹性变形能及系统摩擦耗能等，所以此时系统内各能量均大于其他情况。

表1 不同撞击角度下能量耗散情况

由于计算软件要求被撞击面网格密度必须大于撞击面网格密度，因此撞击面网格密度不能过大，导致钻铤头部只能用多边形近似模拟，钻铤以一定角度撞击时，碰撞点不完全关于y轴对称，撞击时作用力不均匀，导致钻铤发生一定程度的旋转运动。同时，由于撞击角度不同，撞击时板架对钻铤的反作用力的力臂不同，坠物向角度偏移方向倾倒的速度也不同。对质心点运动速度进行合成，通过公式计算出钻铤的动能小于系统输出的坠物动能，说明此时系统输出的坠物动能也包括钻铤坠物旋转运动所产生的动能。坠物以一定角度撞击甲板面时，坠物同时具有绕自身轴向旋转和向一侧倾倒运动，这将导致坠物穿透甲板面时破口有不同程度的扩大，导致板架的塑性变形能增大。

（3）碰撞力

不同角度撞击时碰撞过程中的碰撞力变化曲线如图17所示。可见，坠物垂直撞击时的最大碰撞力最大，α = 5°时的最大撞击力大于α = 10°时。

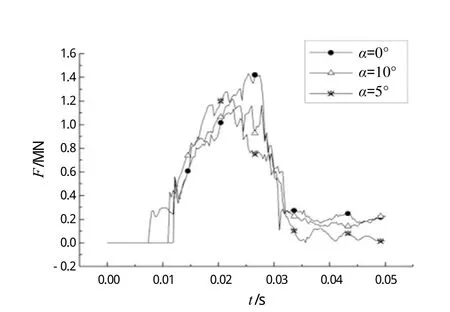
图17 碰撞力-时间历程曲线

综上分析，垂直撞击下的最大碰撞力最大，但从撞击结束后对下方结构的威胁程度来看，这三种碰撞角度中，α = 5°撞击的情况最危险。当α＜45°时，α越大，冲击甲板面的力越小，但是冲击甲板面的截面越尖锐。

为了探索坠物与竖直方向成何种角度撞击时的情况最危险，将α分为0°～10°共11种情况，探索相同时间内哪种情况下坠物穿透甲板的部分最多，哪种情况坠物动能耗散的最慢以及哪种情况最危险。11种情况下坠物的位移时历曲线如图18所示。可见，当α = 1°时，此时坠物穿透甲板板架后的位移最大，反映出在这种情况下坠物动能耗散最少。由于α = 0°撞击时，接触面并非尖角接触而是面与面接触，此种接触模式下坠物穿透甲板面的时间和耗费的能量比尖角接触大很多，因此0.5 s后坠物穿透甲板面后的位移最小。由此可见，在保证尖角首先接触甲板面时，坠物与竖直方向夹角越小，对平台下部结构威胁越大。

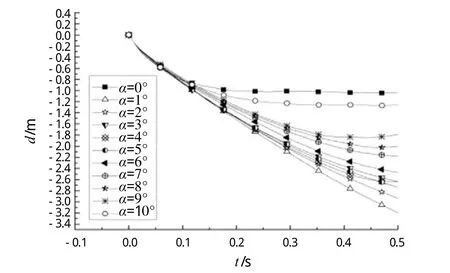
图18 位移时历变化曲线

4 工程安全指导建议

4.1 安全公式推导

针对钻铤坠物垂直撞击在板中央这种最危险情况，推导板架被穿透时的变形能和多种碰撞参数的关系公式。由上述分析可知，坠物动能损耗主要的表现形式转化为板架变形能，其他形式的能量非常小，因此可利用推导出的板架变形能公式，反推坠物穿透甲板板架的临界动能，从而得到最大的坠物下落高度。钻铤坠物参数同本文第1.1节中保持一致，具体工况及结果见表2。

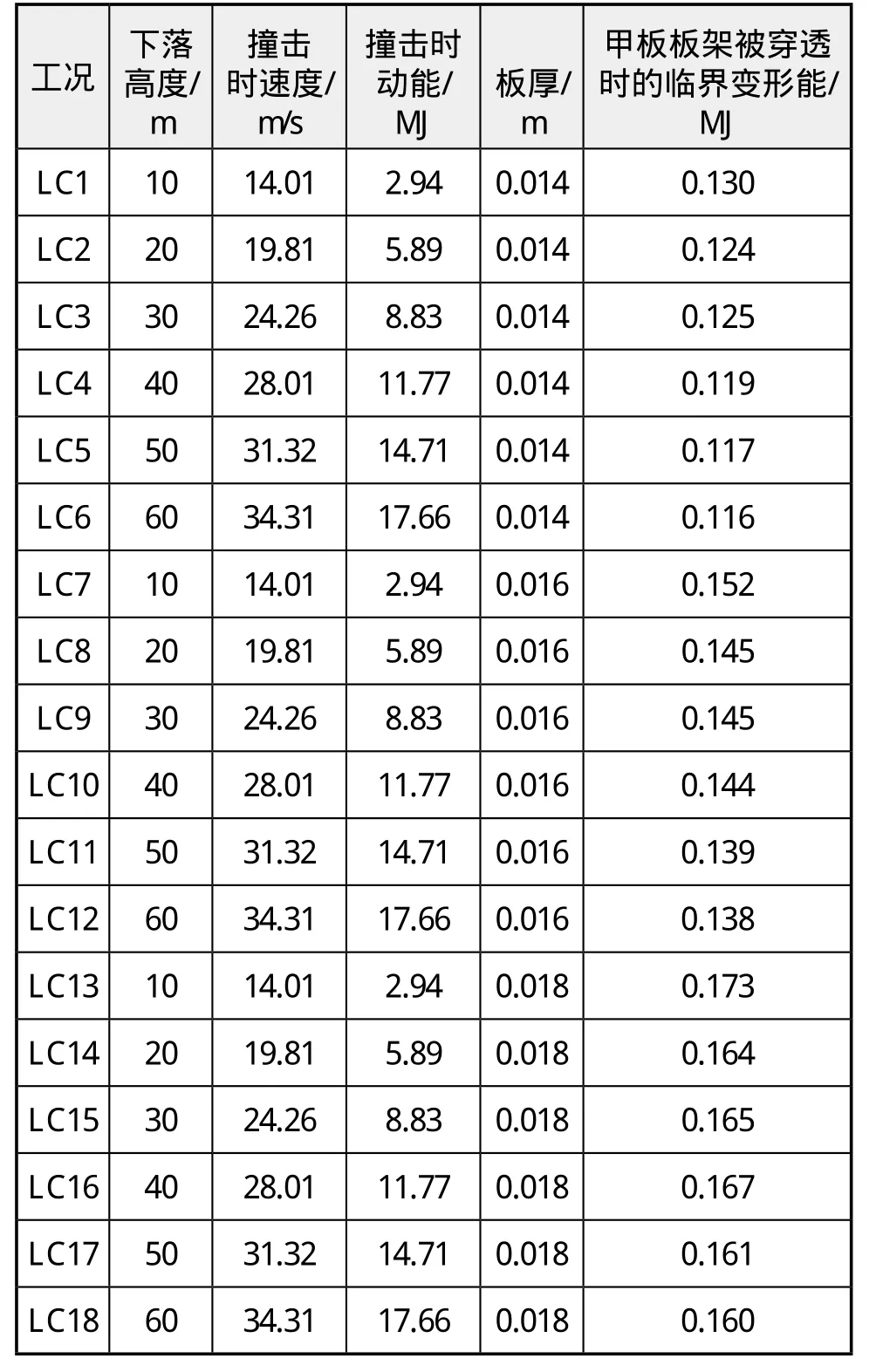
表2 具体工况与结果

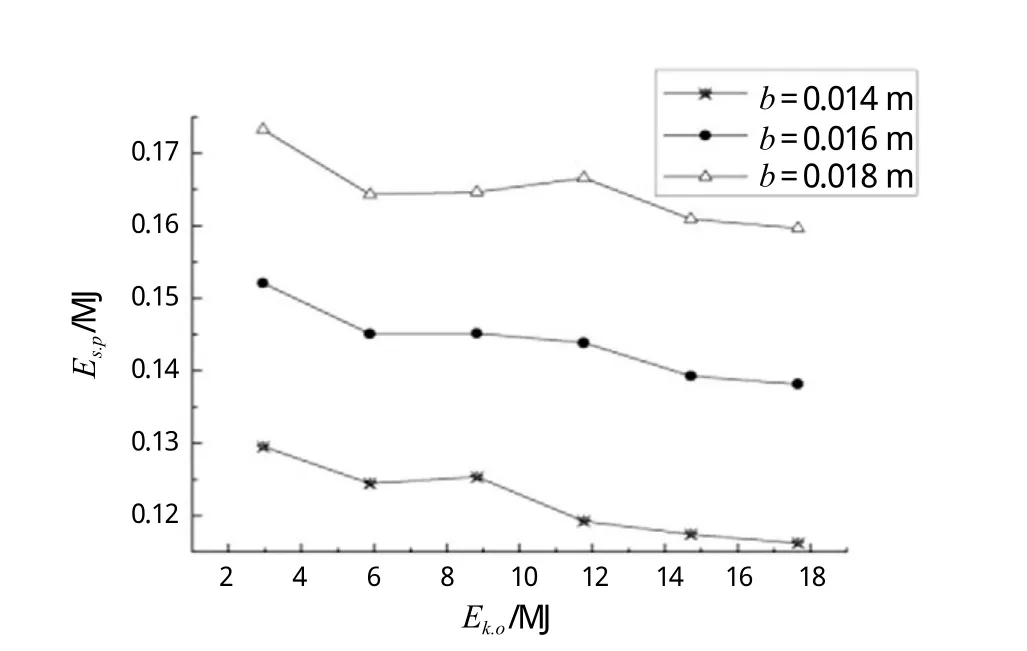
图19 板架被穿透时的临界变形能和坠物碰撞时的动能关系曲线

对板厚b = 0.016 m的曲线进行多项式拟合，拟合情况如图20所示。

图20 板架被穿透时的临界变形能和坠物动能关系拟合曲线

结合能量守恒定律和图20中的曲线多项式拟合结果，可得板架被穿透时的临界变形能公式为:

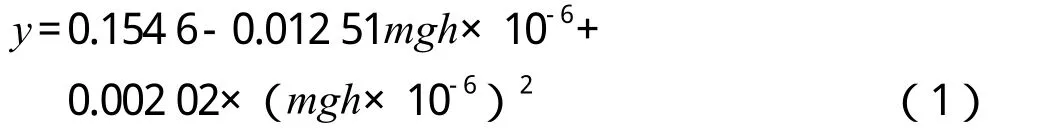
由图19可知，不同板厚下曲线几乎是平行的，因此对板厚和板架被穿透时的临界变形能进行深入研究，将板厚分别设置为0.010 m、0.012 m、0.014 m、0.016 m、0.018 m和0.020 m，坠物质量设置为3172.8 kg，设坠物距平台甲板面10 m处开始坠落，最终得到甲板板架被穿透时的临界变形能和板厚的关系曲线（见下页图21）。

由图21可知，在相同撞击动能下，甲板板架板厚的板架被穿透时的临界变形能关系是线性的，

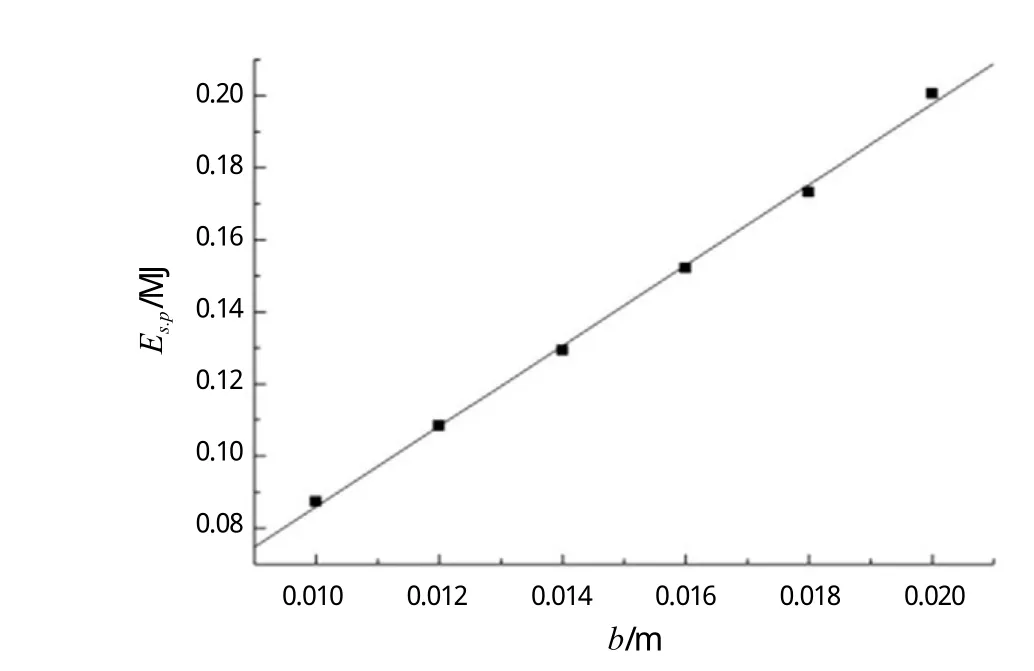
图21 板架被穿透时甲板板架临界变形能关系曲线

经拟合可知，该直线的函数关系为:

借助式（1）和式（2）可推导出不同板厚下甲板面被穿透的临界变形能:

式中:Y为甲板板架被穿透时的临界变形能，MJ；b为甲板的厚度，m。

当mgh≤Y时即可视为安全，即

式中:m为坠物质量，kg；b为板厚，m；h为起吊高度，m；板架变形能和坠物动能的单位为MJ。

4.2 安全公式验证

为了验证上述推导公式的正确性，将数据代入式（3）并与计算结果对比情况见表3。可见，由式（3）推导出的结果与软件计算值吻合，误差非常小，并且改变坠物质量和板厚以及坠物坠落高度后，公式计算结果和有限元软件计算结果误差仍非常小，因此该公式也可应用于工程实际，且具有较高的适用性。

4.3 骨材尺寸对安全公式的影响

下面探讨骨材尺寸对上述推导公式的影响:原骨材纵骨尺寸为L 0.109×0.024×0.008/0.016 m，加强后骨材尺寸为L 0.13×0.024×0.01/0.016 m，原横梁尺寸为m，加强后骨材尺寸为m。板厚b = 0.016 m，坠物质量m = 3000 kg，分别从距离板架10 m、20 m、30 m、40 m、50 m、60 m高度处向下坠落。计算分析得到的坠物动能和板架被穿透时的临界变形能关系曲线如下页图22所示。

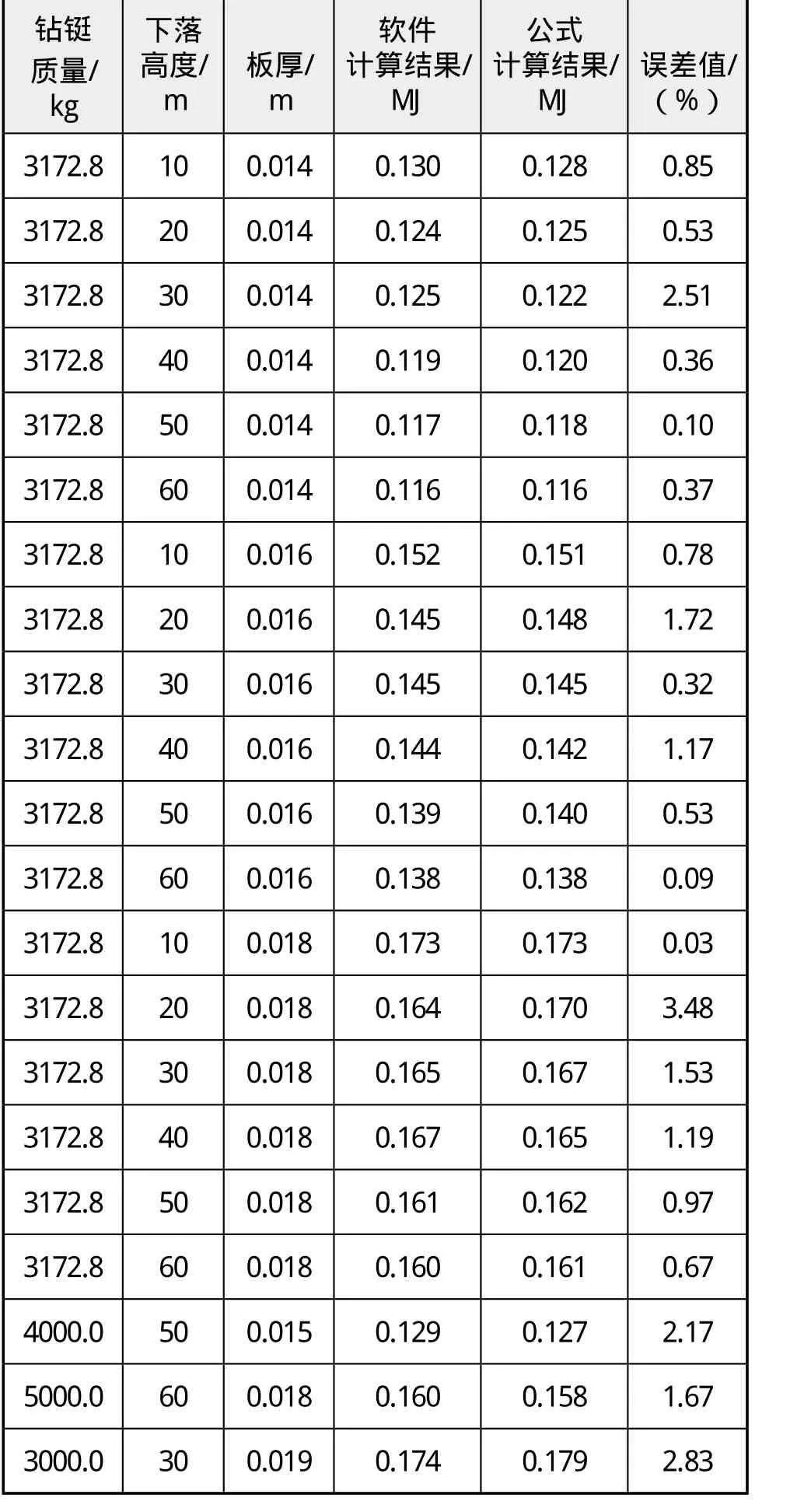
表3 误差对比

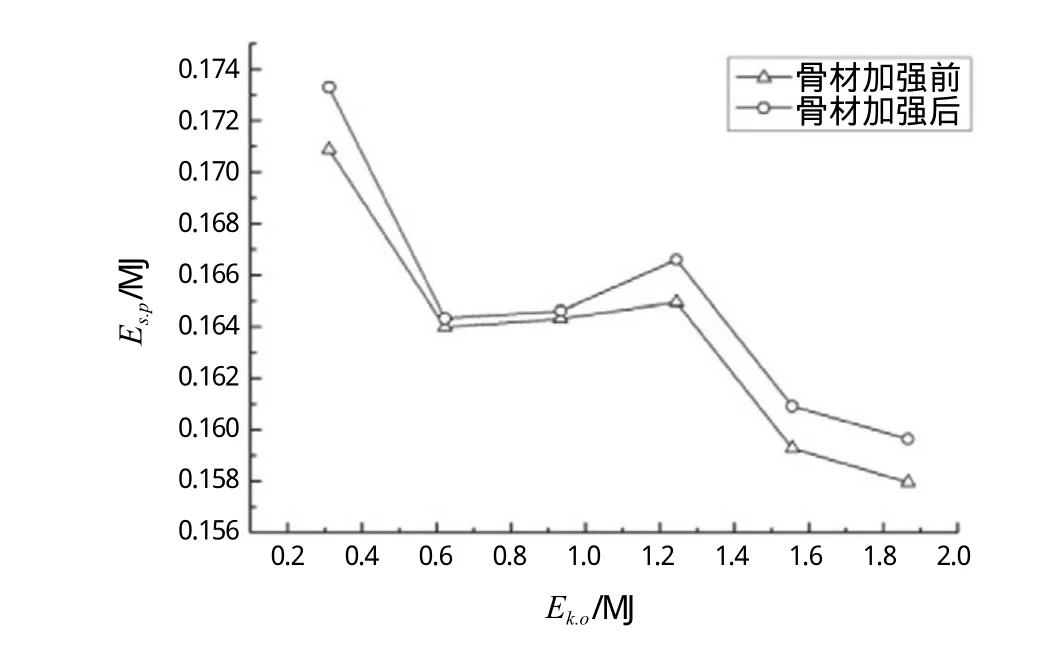
图22 板架被穿透的临界变形能和坠物碰撞动能关系曲线

由图22可见，骨材加强后甲板被穿透时的临界变形能并未发生很大改变。由于钻铤撞击平台甲板时，无疑撞击到甲板板上的情况是最危险的，也是最容易穿透平台甲板的情况，而钻铤碰撞时的接触面积非常小，并且撞击时作用时间短，对骨材的作用不明显，因此加强骨材尺寸对加强平台甲板抵抗钻铤坠物撞击能力的作用并不大。

综上所述，提高平台甲板板抵抗钻铤坠物撞击的能力应考虑对平台甲板板厚进行加强，而无需考虑对平台甲板板架骨材进行加强。另外，也可考虑在甲板平面铺设一层橡胶，以增强甲板面的弹性，延长碰撞的作用时间，也可一定程度上提高平台甲板抵抗坠物撞击的能力。

4.4 撞击角度对公式的影响

将坠物与竖直方向夹角设置为从0°～10°这11种情况，将坠物分别撞击到板厚为0.018 m和0.020 m这两种加筋板的中央，撞击速度v =14.01 m/s，其他参数与本文第1.1节中设置相同（如图23所示），当坠物与竖直方向成5°角撞击时，板架的变形能最大，大约比垂直撞击时板架的变形能多出1%～2%，此时甲板面的塑性变形程度也最大。此外，其他撞击角度下板架变形能都小于垂直撞击的情况。因此，考虑坠物以一定角度撞击甲板面时，可将上述推导出的公式预留出2%的安全裕度，以确保工程实际的安全。

图23 不同撞击角度下板架最大变形能

4.5 坠物横截面积对公式的影响

将半径r分别为0.1 m、0.11 m、0.12 m和0.13 m，内径ri为0.038 m，长L 为9.45 m，质量m分别为3172.8 kg和2800 kg的钻铤坠物以v = 14.01 m/s的速度冲击甲板面，碰撞结束后，板架的变形能曲线如图24所示。

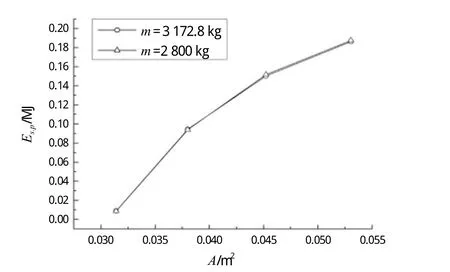
图24 板架变形能曲线

从图24可以看出，不同坠物质量的曲线几乎重合，而曲线的斜率非常大，可见坠物横截面积对板架变形能的影响是巨大的。对曲线进行多项式拟合（如下页图25所示），对式（3）进行修改，加入坠物横截面积的影响，由于式（3）的坠物的横截面半径r = 0.125 m ，横截面积A1= 0.049 m2，将其设为x1，利用公式可求出该坠物半径下的板架变形能，设为y1，已知坠物的半径为r，坠物横截面积A2=3.14×r2，设为x2，因此利用式（3）和图25所拟合出的曲线公式即可推导出最后的计算板架变形能的曲线，各变量单位与式（3）中保持一致:

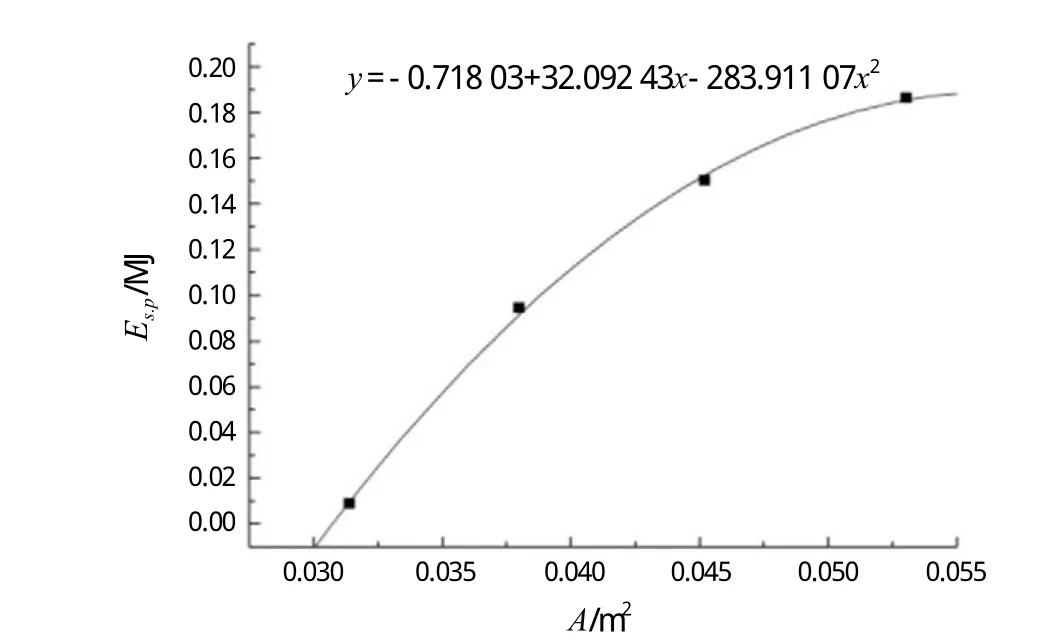
图25 曲线拟合结果

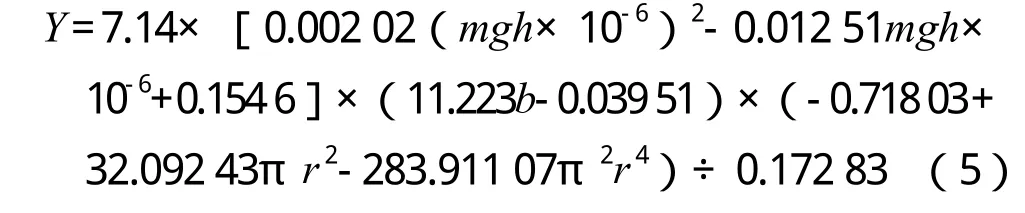
但需注意的是，本公式是针对坠物撞击在平台甲板板中央这种最危险情况，可间接确定坠物的最大下落高度。

5 结 论

通过上述计算和分析，得到以下主要结论:

（1）应用数值仿真技术得到的数据与实验方法得到的数据较好吻合，其结果真实可信。

（2）钻铤坠物撞击甲板板架时只会对甲板面造成局部破坏，并且破口非常小，周围结构不会产生很大的塑性变形，但是钻铤坠物很容易穿透甲板面，对甲板下方结构造成威胁。

（3）钻铤坠物问题与碰撞点甲板下方支撑构件强度有关，支撑构件越强，碰撞越强烈，但坠物动能消耗越多，钻铤坠物撞击到甲板板中央这种情况是最危险的。

（4）坠物以一定角度撞击时，在保证尖角截面首先接触甲板面时，坠物与竖直方向夹角越小，穿透甲板后的位移越大，坠物动能消耗越少。坠物与竖直方向夹角为5°左右时，板架变形能最大，甲板板架的塑性变形最大。

（5）根据数值仿真分析结果拟合出的计算板架被穿透时的临界变形能的公式具有较高的适用性，可在一定程度上指导工程实践。

［1］郝瀛.物体坠落对平台甲板冲击破坏的判据研究［D］. 哈尔滨:哈尔滨工程大学硕士学位论文，2009.

［2］张海，刘蕊，王秀存，等. 坠落物体产生的冲击载荷对海底管线的损伤分析［J］. 海洋技术，2008（1）:77-80.

［3］DNV.Design against accidental loads［S］. Recommended practice DNV-RP-C204. October 2010.

［4］BV. Rules for the Classification of Offshore Units［S］.2013.

［5］WENGER A. Design for Impact of Dropped Objects Annual Offshore Technology Conference［C］. 1983.

［6］AL-Obaid Y F. Automated analysis of topside platform hatch covers subject to drill collar impact［J］. Computers and Structures. 1996（5）:665-689.

［7］林一，熊飞，胡永利.典型海洋平台在位情况下碰撞分析及算例研究［J］. 中国海洋平台，2012（10）:27-33.

［8］Introduction to MSC Dytran. DYT101 Seminar Workbook.Europe. Corporate［S］. Asia Placific:MSC Software Corporation，2008.

［9］程正顺，胡志强，杨建民 半潜式平台结构抗撞性能研究［J］. 振动与冲击，2012（4）:38-43.

［10］王自力，张延昌.基于夹层板的单壳船体结构耐撞性设计［J］. 中国造船，2008（3）:60-65.

［11］程晓达，曹冬梅，尹绪超，等.典型补给油船抗冲击性能研究［J］.船舶，2012（1）:33-37.