议强化高中数学圆锥曲线教学的策略
周浩
【摘 要】圆锥曲线部分的知识是高中数学的重点和难点,在高考中所占的分数较大,得分率不高。本文从自己的实际教学出发,提出了强化圆锥曲线部分教学有效性的相关策略,希望能够对广大高中数学的教师有所帮助。
【关键词】圆锥曲线 教学 计算能力 重点
中图分类号:G4 文献标识码:A DOI:10.3969/j.issn.1672-0407.2014.08.092
在高考数学中圆锥曲线知识所占的分数比重很大,每年都会有一道相关的大题,在选择和填空题中也出现对相关知识的考察。圆锥曲线题目通常灵活性较强,解答的难度较大,得分率不高。在日常的教学之中,也花费了大量的时间在圆锥曲线知识上,但是取得的效果并不是十分明显,这使教学面临了很大的困难。
一、准确把握教学的难点、重点
圆锥曲线知识的主要内容有抛物线、双曲线和椭圆。这三个内容之间有着一定的联系,其中对于双曲线的知识,在教学中的要求相对较低,只是让学生掌握双曲线的一些有关定义和概念,对其图像和基本性质有所了解,在考试中涉及到双曲线知识的问题难度通常不会太大。但是抛物线和椭圆是圆锥曲线知识教学的难点和重点,在教学中不但要让学生准确的掌握其基本性质,还要做到对知识的灵活运用。所以,在实际的教学中要以椭圆和抛物线的知识为教学的难点和重点,对其给予足够的重视,努力做好相关的教学,提高学生对知识的运用能力。
二、教学中加强对学生计算能力的培养
在高考数学中,学生普遍反映答题的时间不够,就算多给一点时间,有的题目也无法解答完整。其实这并不是出题的原因,是学生的解题速度和计算能力达不到一定的标准,高考也是对学生计算能力的一种考察。在进行圆锥曲线部分的教学中,要加强对学生计算能力的培养,我们要做好以下几个方面的工作:
首先,在平时的就学习过程中,鼓励学生亲自动手计算,解决问题,禁止学生运用一些计算辅助设备,为学生设置规定的时间,训练计算能力,在提高计算速度的同时还要保证计算的准确率;其次,对学生的计算步骤进行规范,许多高中生一味的追求计算速度,不重视计算步骤的规范,使得在计算中经常出现错误,得不到准确的结果,造成了时间的浪费;再次,要强化对算法和算理的讲解,向学生强调算法的重要意义,在学生能够熟练地掌握有关计算之后,再简化计算的步骤,使得运算的速度得到提高;与此同时,掌握正确的算法和算理还能够帮助学生总结在运算中遇到的一些特殊问题,自主的找到解决问题的方法;最后,选择有效的计算方法,对于同一个问题,有不同的计算方法,在解题时,要进行全面的思考和判断,找到最佳的解题方法和思路,在最短的时间内解决问题。
三、结合图形进行问题的解答
学生在刚刚接触到圆锥曲线部分的知识时,很难理解学习的内容,也不知道该用什么方法和思路进行问题的解答,必须要经过一段时间进行理解和消化。在这段时间内教师要充分利用圆锥曲线的图形,开展好教学工作,利用直观的图形,在学生脑海中建立起有关的概念,结合图形进行问题的讲解,运用数形结合思想做好教学的工作。虽然在解析几何部分学生已经接触到了数形结合的教学,但是那时的教学内容比较简单和单一,不能很好的理解和运用这种思想。圆锥曲线的有关问题十分繁琐和复杂,利用图形可以将抽象的问题形象化,降低题目的难度,同时还能帮助学生更好的理解有关的性质和概念。所以,在教学中做好数形结合,帮助学生养成画图的好习惯。
已知曲线C:y=x2和直线M:x-y+2=0相较于点P(xp,yp)和Q(xq,yq),xp小于xq,曲线在点P、Q之间的部分为l,二者所围成的区域为D,设l上的一点为A(a,b),同时,A、P、Q三点不重合。
1. 假如PQ的中点为B,求线段AB中点T的运动轨迹。
2.假如曲线G:x2-2ax+y2-4y+a2+51/25=0和D存在公共点,求a的最小值。
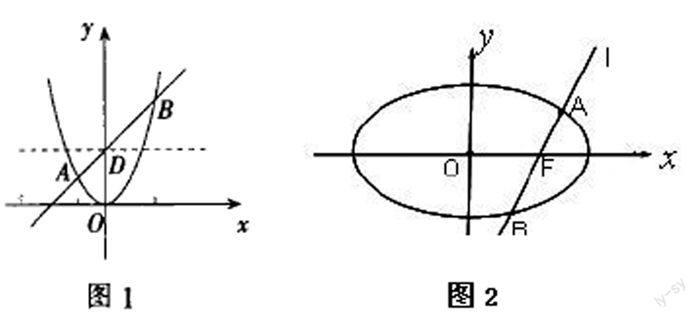
解析:这是09年广东高考中的一道题目,主要考查了直线和抛物线的位置关系、曲线轨迹方程的求法和曲线之间的位置关系。本题的重点是曲线 G的圆心在直线y=2上,G和D有公共点,在A的值最小的情况下,到底是G和D相交与点P还是与直线M的切点,这就需要我们画图进行分析,在本题中没有给出相应的题目,需要学生理解题目的含义,画出相关的图形。如图1所示:
四、借助向量知识进行问题的转化
学生在掌握了数形结合的方法之后,要想更好的学好圆锥曲线的知识,还需要在解题中运用向量部分的知识,进行问题的转化。在目前高考数学题目的设置上,越来越多的将圆锥曲线知识和向量、数列、不等式和导数等知识相结合,加强了对学生综合能力与知识运用能力的考查,这也说明数学知识之间是相互联系的。其中圆锥曲线的知识和向量知识之间的联系颇为紧密,在向量知识中既有一些代数的特征又涉及到图形的知识,把几何与代数有效的结合在一起,在解答圆锥曲线的问题时,我们可以将其中的几何关系通过向量的形式表现出来,进行向量计算,再转化为几何结论,这种转化能够使问题的难度降低,节省解题的时间。凡是在圆锥曲线问题中涉及到角度、长度的计算和垂直、平行等位置关系时,我们都可以使用向量知识进行解答。
如图2所示,椭圆x2/a2+y2/b2=1(a>b>0)的一个焦点F(1,0),O为坐标原点。(1)已知椭圆短轴的两个三等分点与其中一个焦点构成正三角形,求椭圆的方程;(2)设过 F 点的直线 l 交椭圆于A、B 两点。若直线l绕点F任意转动,恒有|OA|2+|OB|2<|AB|2,求a的取值范圍。
解:设A(x1,y1),B(x2,y2)当直线AB与x轴重合时,|OA|2+ |OB|2=2a2,|AB|2=4a2(a2>1),因此恒有|OA|2+ |OB|2<|AB|2。当直线AB不与x轴重合时,设直线AB的方程为:x=my+1,代入椭圆方程整理得:(a2+b2m2)y2+2b2my+b2-a2b2=0因此求得y1+y2和y1y2的表达式。又因为恒有|OA|2+ |OB|2<|AB|2,所以∠AOB是钝角。也就是说向量OA与OB的向量积恒小于零。所以在m取全体实数时,m2a2b2+b2- a2b2+a2<0 也就是b2- a2b2+a2 以上就是对高中数学圆锥曲线教学的有效策略分析。结合自己的实际教学情况,提出了强化圆锥曲线教学效果的有关策略,目的在于帮助广大教师做好该部分的教学工作,提高学生高考的得分率。

