电感参数对IPMSM转子位置估算的影响

2014-09-20 06:07于艳君柴凤高宏伟程树康

电机与控制学报 2014年7期

于艳君，柴凤，高宏伟，程树康

(哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨 150001)

电机的电磁转矩方程

0 引言

内置式永磁同步电机由于高功率密度、高转矩密度、宽调速范围等优点而得到了越来越广泛的应用［1］。大多数永磁同步电机的高性能控制算法均需要提供电机转子的位置信息，通过机械式传感器可获得这一信息，但其增加了系统的成本。因此，无位置传感器控制成为了电机领域的重要研究方向。

在众多的转子位置估算方法中，高频信号注入法由于可实现IPMSM在低速甚至零速下的无位置传感器运行而得到广泛应用［2－6］。该方法利用电机d、q轴电感的不同，利用高频电压激励得到的高频电流响应方程，依据电感的空间凸极性来估算转子的位置信息。一方面，利用高频信号法在推导转子位置估算公式时，一般是在假设d、q轴电感不变的前提下得出的。而在电机的实际运行过程中，随着定子电流的增加，电感参数除具有空间凸极特性外，还会呈现出饱和凸极性及交叉耦合凸极性［7－8］，这种饱和凸极性和交叉耦合凸极性的存在势必会造成电机d、q轴电感的变化，进而影响转子位置的估算精度。另一方面，高频信号法一般要求向电机绕组中注入特定的高频信号，存在着高频信号频率和幅值的选择问题。文献［9－10］提出了一种利用PWM逆变器本身的载波频率成分信号作为特定高频信号以实现IPMSM无位置传感器控制的方法，有效避免了高频信号注入法的不足，并对利用三相三角载波SPWM调制方式产生的载波频率信号进行转子位置估算的原理进行了详尽研究，但并未分析d、q轴电感变化对转子位置估算的影响。

本文在文献［9－10］研究的基础上，对d、q轴电感参数对转子位置估算的影响进行分析。为此，本文首先给出了基于载波频率成分信号法进行电机转子位置估算的原理，并以一台10极/12槽集中绕组样机为例，在研究电机饱和凸极性及交叉耦合凸极性对电感参数影响的基础上，分析电感参数对转子位置估算的影响，并进行相应的仿真和实验研究，以验证理论分析的正确性。

1 IPMSM转子位置估算原理

为了产生用于转子位置估算的旋转高频电压信号，本文采用三相三角载波SPWM调制方式，其三相载波信号如图1所示。

利用该调制方式时，在静止的α－β轴系下，逆变器输出载波频率成分电压信号近似为

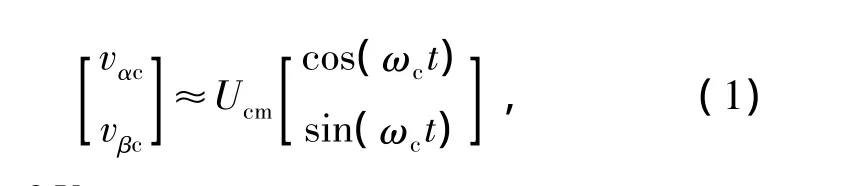
图1 三角载波波形Fig.1 Triangular carrier wave form

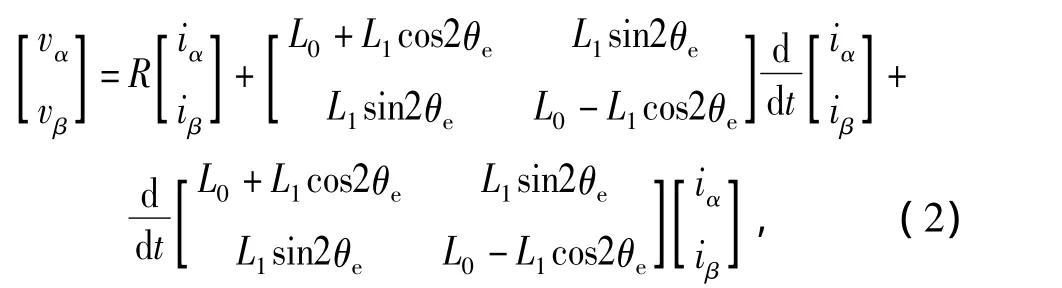
式中:L0=(Lq+Ld)/2为平均电感;L1=(Lq－Ld)/2为半差电感;Ld为零电流下的d轴电感;Lq为零电流下的q轴电感。θe为α轴与d轴间的空间电位置角;R为电机绕组电阻。

由于载波频率ωc远高于电机基波频率ωm，故在载波频率下，电机的电阻压降及电感变化引起的压降与高频电流的阻抗压降相比可以忽略不计。其电压方程可表示为

式中，下标c表示高频载波频率成分分量。

由式(3)可得iαc、iβc的解析式，即

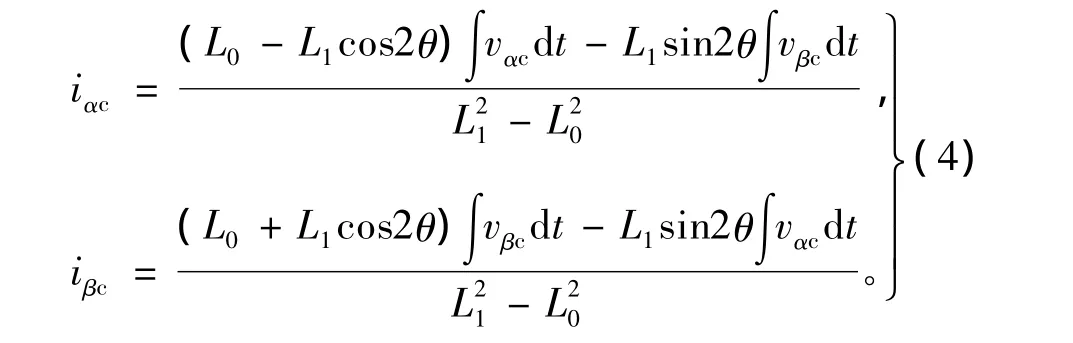
式中，iαc、iβc分别为电机 α、β 轴的载波频率成分电流。

由式(4)可得载波频率成分电流包络线方程为

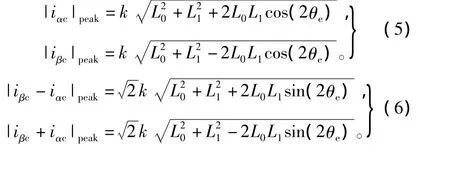
式(5)、式(6)中含有转子的位置信息:sin2θe、cos2θe，对方程进行开平方整理后可得到电机转子位置的估算公式为

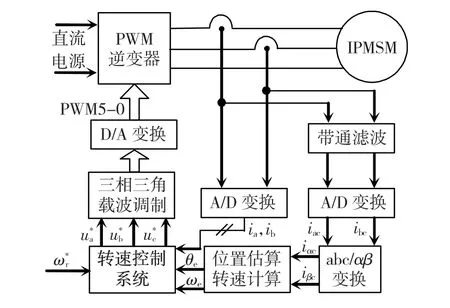
图2 系统的原理框图Fig.2 The basis structure of the system

2 电感参数对位置估算的影响

上述对转子位置的估算式(7)是在假设d、q轴电感不变的情况下推导得出的，但电机实际运行过程中由于永磁体的存在，使得永磁同步电机的铁心工作在近饱和状态。一方面，电机系统的磁饱和造成d、q轴电感随绕组电流的变化而变化。另一方面，电机绕组的d、q轴磁路之间存在交叉耦合，这两方面势必会对转子位置的估算精度造成影响。

2.1 饱和对电感及转子位置估算的影响

为了分析电感参数对转子位置估算的影响，需要准确分析不同电流时电机电感的变化。本文以一台10极/12槽IPMSM样机为例进行说明。10极/12槽IPMSM的主要参数为:功率=750 W;额度电流=3.4 A;额度线电压=200 V;额定转速3 000 r/min;永磁体磁链=0.638 Wb;定子每相绕阻=0.505 Ω;平均电感=6.0 mH;极数/槽数=10/12。电机的d、q轴磁路如图3所示。

图3 内置式永磁同步电机的d、q轴磁路Fig.3 d-and q-axis magnetic circuit of IPMSM

图4 所示为所测得的d轴或q轴电感，测量时，将电机a相绕组固定在d轴或q轴，测得的a相绕组的电感即为d轴或q轴电感。

d、q轴电感的计算式为

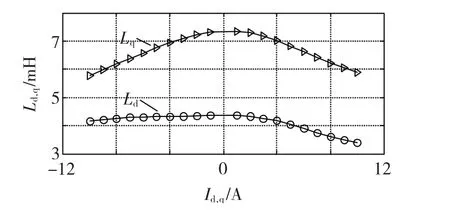
图4 d、q轴电感的实测结果Fig.4 Tested results of d and q-axis inductances

从图4可以得出，随着电流的增加，由于磁路的饱和造成d、q轴电感不再固定为常值，而是随电流变化而变化，电流增加时造成电机凸极比减小。d、q轴电感的变化势必会造成电机转子位置的估算误差增大。

由式(5)可得到高频载波频率成分电流包络线平方的最大、最小值之比，以α轴为例

式中，ρ为电机的凸极比，ρ=Lq/Ld。

对于IPMSM，ρ＞1。对式(10)求微分可得:在ρ＞1时，该式是ρ的增函数。故当ρ变小时，导致电流包络线平方的最大、最小值之比减小，即凸极比变小会造成载波频率成分电流包络线的空间幅值变化变小，这对系统实现时的硬件及软件检测是不利的，使得采样得到的载波频率成分电流包络线分辨率变差。因此，随着负载的增加，定子电流的增加，磁系统饱和引起电机凸极比减小，进而会造成转子位置估算误差的增大。

2.2 交叉耦合对电感及转子位置估算的影响

电流的增加也会引起d、q轴交叉耦合电感的变化，造成位置估算误差。交叉耦合电感的计算式为

图5所示为所给电机模型的交叉耦合电感参数的有限元仿真结果。从图5可见:随着电流的增加，d、q轴之间的交叉耦合电感增加，势必会影响转子位置的估算精度，造成转子位置估算的误差增大。

图5 d、q轴耦合电感的有限元分析结果Fig.5 FEA results of the d-and q-axis cross inductances

3 仿真和实验研究

3.1 考虑饱和及交叉耦合的IPMSM模型

为了分析电感参数对转子位置估算的影响，建立了基于电感饱和和交叉耦合的IPMSM数学模型。

电机d、q轴系的磁链方程为

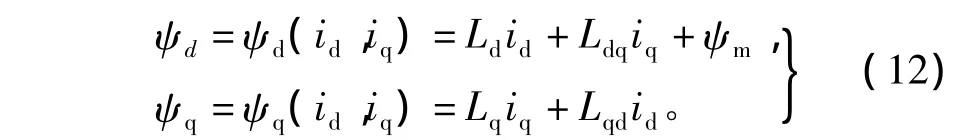
电机d、q轴系的电压方程为

电机的电磁转矩方程

3.2 仿真结果

在上述数学模型的基础上，在Matlab/SIMULINK构建了IPMSM系统的无位置传感器控制模型，进行了相应的仿真研究。仿真中，系统的采样周期设定为10μs，图6所示为电机在35 r/min转运行时空载和负载(2N·m)两种情况下的仿真得到的位置估算误差结果。从仿真结果可以看出:系统在负载时的估算误差大于在空载时的误差，仿真结果验证了理论分析的正确性。

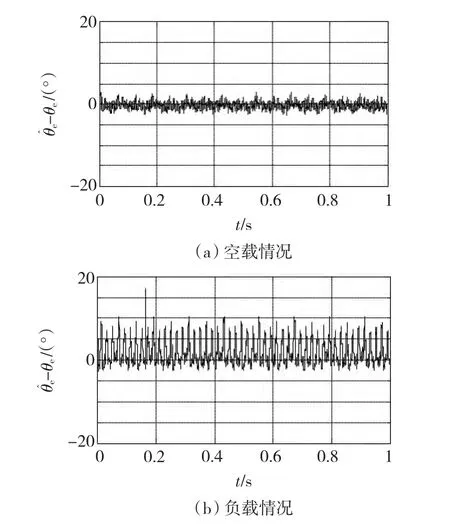
图6 转子位置估算误差的仿真结果Fig.6 Simulation results of the estimated error

为了验证电感饱和造成的电机凸极比变小对转子位置估算的影响，仿真时，改变电机模型中的Ld、Lq的数值进而改变电机的凸极比。图7所示为空载情况下电机在不同凸极比、不同转速下的位置估算误差的仿真结果。

图7 位置估算误差随凸极比、转速的变化曲线Fig.7 The change of rotor position estimated error with saliency and speed

从图7可以看出，随着凸极比的减小，位置误差增大，尤其是在凸极比接近于1时，位置误差已经超过10°，且误差增大趋势明显，验证了前述理论分析的正确性，并且从另一面也说明了高频信号法无位置传感器控制不适用于表面式永磁同步电机的位置检测。

3.3 实验结果

实验时，样机由电压源型逆变器供电，控制器以TMS320F2808为核心，利用模拟带通滤波器获得电机定子电流的载波频率成分，系统每12.5 μs完成一次电流A/D采样，三相载波信号的频率设定为10 kHz。通过软件实现电机转子的位置估算及系统的闭环控制。并在电机上安装增量式编码器以实现对电机实际位置的检测。图8所示为系统实验图，利用Magtrol测功机给电机加载，负载为2 N·m。

图8 实验平台Fig.8 Experimental bench

图9所示为系统在35 r/min时负载时的位置估算结果。实验结果证明了文中所用方法的可行性。

图9 转子位置的实测和估算结果Fig.9 Estimated and real results of the rotor position

图10所示为电机转速在35 r/min时空载和额定负载2种情况下的转子位置估算误差的实验结果。

从图10可得:电机空载时的位置估算误差为－6.0°～2.6°;负载时的位置估算位差为－8.2～4.5°。负载时的误差大于空载时的误差，其主要原因是负载时由于饱和引起的d、q轴电感变化而造成的，这与前面的理论分析相吻合。

图10 转子位置估算误差的实验波形Fig.10 Experimental waveforms of the estimated error

4 结语

本文分析了电感参数变化对内置式永磁同步电机转子位置估算的影响。随着定子电流的增加，电机电感会呈现出饱和及交叉耦合凸极性，使得电机的凸极比减小。在凸极比较小时，载波频率成分电流包络线的最大值/最小值之比减小，不利于包络线检测，从而会导致估算位置误差的增大。

［1］NOGUCHI T.Trends of permanent-magnet synchronous machine drives［J］.IEEE Transactions on Electrical and Electronic Engineering，2007，2(2):125－142.

［2］JEONG Y S，LORENZ R D，JAHNS T M，et al.Initial rotor position estimation of an interior permanent-magnet synchronous machine using carrier-frequency injection methods［J］.IEEE Transactions on Industry Applications，2005，41(1):38－45.

［3］DE KOCK H W，KAMPER M J，KENNEL R M.Anisotropy comparison of reluctance and PM synchronous machines for position sensorless control using HF carrier injection［J］.IEEE Transactions on Power Electronics，2009，24(8):1905－1913.

［4］何栋炜，彭侠夫，蒋学程，等.内置式永磁同步电机转子初始位置估计方法［J］.电机与控制学报，2013，17(3):49－55.

HE Dongwei，PENG Xiafu，JIANG Xuecheng，et al.Initial rotor position estimation method for IPMSM［J］.Electric Machines and Control，2013，17(3):49－55.

［5］王冉珺，刘恩海.永磁同步电机转子初始位置的检测方法［J］.电机与控制学报，2012，16(1):62－66.

WANG Ranjun，LIU Enhai.Method for initial rotor position inspection on of PMSM［J］.Electric Machines and Control，2012，16(1):62－66.

［6］秦峰，贺益康，刘毅，等.两种高频信号注入法的无传感器运行研究［J］.中国电机工程学报，2005，25(5):116－121.

QIN Feng，HE Yikang，LIU Yi，et al.Comparative investigation of sensorless control with two high-frequency signal injection schemes［J］.Proceedings of the CSEE，2005，25(5):116－121.

［7］SERGEANT P，DE BELIE F，MELKEBEEK J.Effect of rotor geometry and magnetic saturation in sensorless control of PM synchronous machines［J］.IEEE Transactions on Magnetics，2009，45(3):1756－1759.

［8］DUTTA R，RAHMAN M F.A comparative analysis of two test methods of measuring d-and q-axes inductances of interior permanent-magnet machine［J］.IEEE Transactions on Magnetics，2006，42(11):3712－3718.

［9］MAMO M，OYAMA J，ABE T，et al.Carrier frequency component method for position sensorless control of IPM motor in lower speed range［J］.Transactions of the Institute of Electrical Engineers of Japan D，2000，120－D(2):275－280.

［10］MAMO M，IDE K，SAWAMURA M，et al.Novel rotor position extraction based on carrier frequency component method(CFCM)using two reference frames for IPM drives［J］.IEEE Transactions on Industrial Electronics，2005，52(2):508－514.