一种用于高精度随动控制系统的轨迹预测方法
巫佩军, 杨文韬, 余驰, 杨耕
(1.清华大学自动化系,北京 100084;2.庆安集团有限公司,陕西西安 710000)
0 引言
在某些高精度随动控制系统运行中,往往面临目标被短时遮挡导致轨迹不连续,或给定周期过大的现象,从而导致随动系统跟踪响应变慢、特性变差等问题。为了达到对目标的稳定持续跟踪、提升对目标的跟踪质量,在工程上一般采用轨迹预测的方法。实用的方法主要有卡尔曼滤波[1]、最小二乘[2]和模型预测[3]等。其中,卡尔曼滤波预测算法对目标的轨迹预测效果较好,且不需要存储以前的数据,还可以获得系统其它状态信息。但算法需要精确的系统模型,建模误差会给系统带来较大影响。最小二乘预测算法运算简单,计算量少,易于工程实现[4],但拟合函数的通用性不强,在轨迹类型发生变化时预测效果变差。模型预测控制是一种基于模型的控制算法,在控制时域内最小化目标函数以求出最优控制律。建模误差也会对这一方法的控制效果带来影响。
此外,普通随动控制器运算能力较低,难以完成比较复杂的控制算法,因此难以满足系统具有较高控制精度这一需求[5]。为了改进此问题,本文以两自由度高精度随动控制系统为研究对象,提出了一种适用于不同类型轨迹的预测算法。首先对被跟踪轨迹进行微分判定并分类,据此选择适当的拟合函数以及预测步长;其次,采用最小二乘法作为轨迹预测方法,通过提供完整的目标轨迹信息,或等效提升位置给定速率,提升系统的性能。文中以连续可导的正弦波和不可导的三角波两种轨迹为例预测,结合仿真验证和实物实验,对轨迹预测效果进行综合分析,验证了该预测方法的可行性。
1 两自由度随动控制系统
两自由度随动控制系统结构如图1所示。随动控制器接收上位机的跟踪指令,通过对指令和反馈信号的处理,对执行机构水平、俯仰电机发出控制指令;执行机构按照指令,通过传动装置,将被控对象移动到指定位置来跟踪目标;水平、俯仰编码器,将采集到的被控对象位置信息,反馈给随动控制器;随动控制器还会将系统工作状态传回上位机。

图1 随动控制系统原理图Fig.1 Schematic of servo control system
不考虑负载扰动和测量噪声,随动数字控制系统如图2所示。Tr、Ty、Tu分别代表输入r(t)、输出y(t)和控制u(t)指令周期。Tu由D/A转换器和控制器的速度决定,为随动控制系统控制指令周期;Ty一般由传感器的速度决定,是系统采集信号的周期;Tr为随动系统收到的指令周期。当Tr<Tu,Ty时,采用轨迹预测的方法,可以等效提升轨迹给定指令周期,从而提升系统性能。
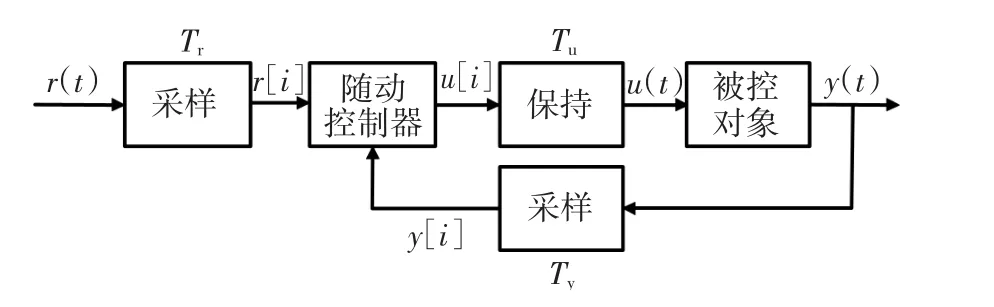
图2 随动数字控制系统Fig.2 Digital servo control system
2 轨迹预测
最小二乘法轨迹预测,是一种利用已知轨迹,采用多项式函数拟合,预测未来轨迹的方法。由于其拟合多项式不随着轨迹变化,所以在确定了拟合多项式后,针对不同类型的轨迹,其预测效果也不相同。在基本预测方法的基础上,通过对轨迹类型的判断,选用不同的拟合函数,会提升预测效果。
2.1 预测原理
己知前n个时刻的位置给定(xi,yi),i=1,2,…,n,假定多项式拟合函数T(t),使得拟合误差(实际位置与拟合曲线的距离)的平方和D最小。拟合函数为
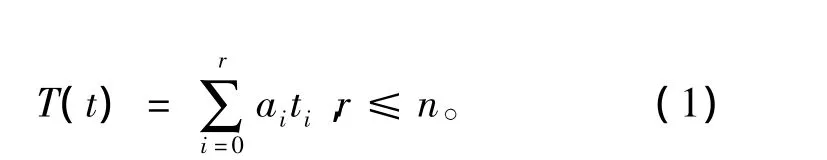
其中:ai为待定系数,ti为时间。拟合误差平方和为

拟合问题变为:求待定系数ai,使得D取最小值。根据多元函数极值的必要条件:函数在某点具有偏导数且偏导数为零。我们以估计x轴位置为例,得

整理后得到
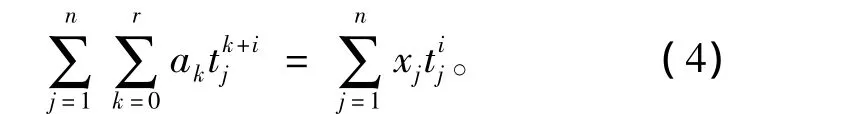
于是,上述拟合问题转化为求以下方程的解[a0,a1,…,ar][6-7]为

仿真中分别为对正弦波和三角波的预测,仿真结果如图3所示,图中菱形为位置给定值,圆点是对位置给定值的估计(图4、图5、图7同)。从图中可以看到,轨迹预测可提高实际系统中给定信号的频率。这种轨迹预测方法,对于连续的、平滑变化的位置给定(图3(a)),具有较好的预测效果,可以准确预测连续两次位置给定之间的位置信息。但是对于三角波(图3(b)),由于其在尖点处不可导,对于此点之后的估计并不准确。即在知道尖点处的位置给定时,没有任何信息可以预示位置给定斜率的剧烈变化,因此在下一次位置给定到来之前的时间内,对于位置的估计值都是不准确的。
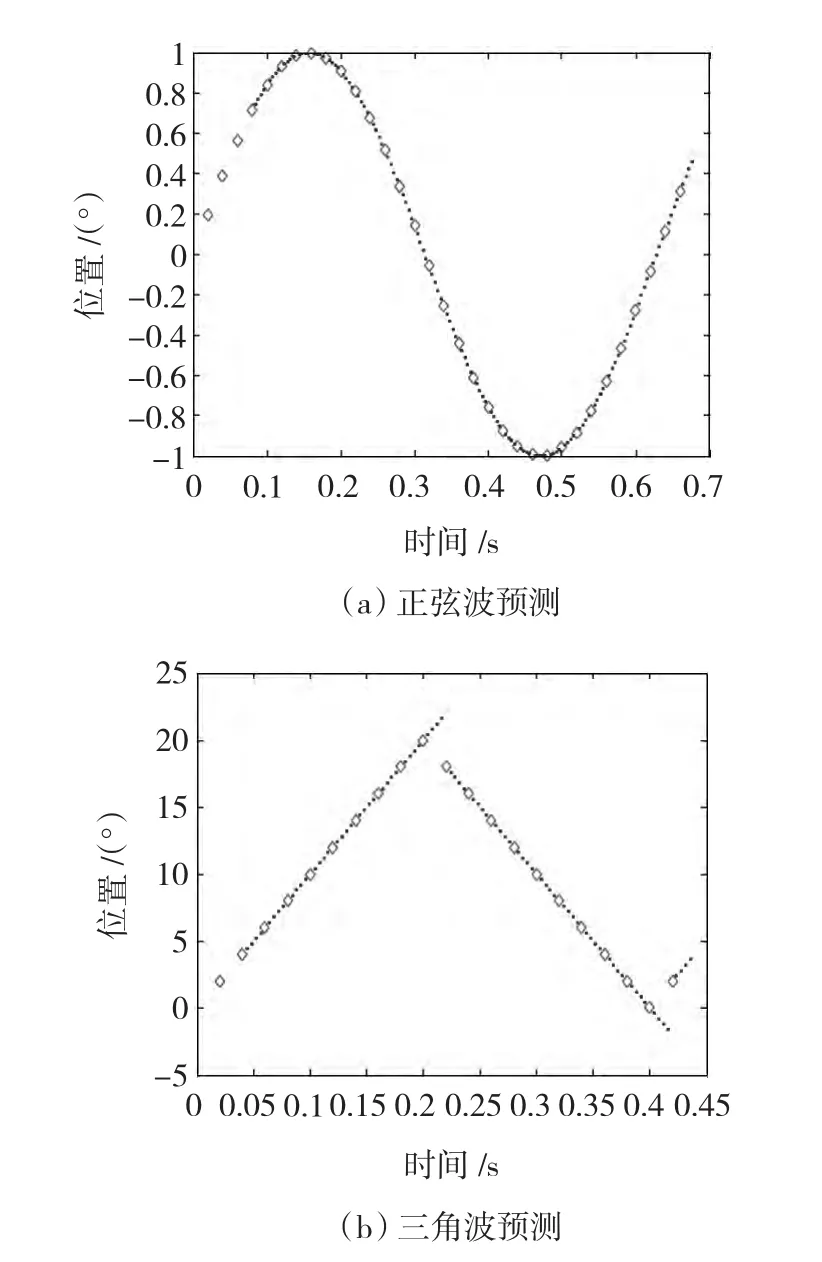
图3 轨迹预测仿真Fig.3 Simulation of trajectory prediction
实际系统中,位置给定对应于跟踪目标的实际位置。由于被跟踪的目标具有较大惯性,因此其位置是连续变化的,这就使得本文提出的预测方法更为有效。
2.2 预测算法的选择
由于目标轨迹具有多变化、不确定和随机性,采用基于最小二乘法的多项式拟合预测目标移动轨迹时,如果能够根据目标的已知轨迹,优化预测步长,亦即优化拟合多项式函数T(t)的多项式阶数,对于提升预测方法的准确性,有较大帮助。这是因为对于任意轨迹,若设置的多项式阶数过高,则式(4)左侧的方阵A的阶次会变高。经仿真验证,当A的阶次超过10阶时,A往往会变为病态矩阵,此时求出的多项式系数[a0,a1,…,ar]会不准确,导致预测效果变差。
同时,由于已知的历史数据具有误差,预测结果也会引入误差。此时,对于同一轨迹采用不一样的多项式拟合函数,历史数据误差带来的影响也不同,适当的选取拟合多项式,会减小这一误差。我们以原函数为一阶多项式为例,说明采用一阶、二阶拟合多项式后,带来的误差不同。
设原多项式为Y(t)=t+1,已知的3个点为

采用一阶、二阶多项式拟合函数在t+2处的值,所得结果如表1所示。

表1 一、二阶拟合多项式拟合结果Table 1 Fitting results with first and second order polynomials
可见,不同拟合多项式拟合结果不同。对于由历史数据误差带来的拟合误差,选取合适的拟合多项式,会减小这一偏差。以下以目标轨迹为三角波和正弦波为例,说明拟合函数对不同轨迹预测效果的影响。
若历史轨迹为三角波,对轨迹微分可知,在大多数位置,微分结果为常数。此时,可适当降低拟合多项式阶数,采用一阶或二阶多项式参与拟合,会提升轨迹预测效果。图4为不同阶次对三角波轨迹预测结果影响对比。
由图4可见,对于三角波轨迹预测,一阶多项式得到的结果要优于高阶多项式。同样的,若历史轨迹为正弦波,轨迹任意阶可导,则可以采用较高阶数的多项式参与拟合。经仿真验证,当多项式阶数为3时,仿真效果较为理想。
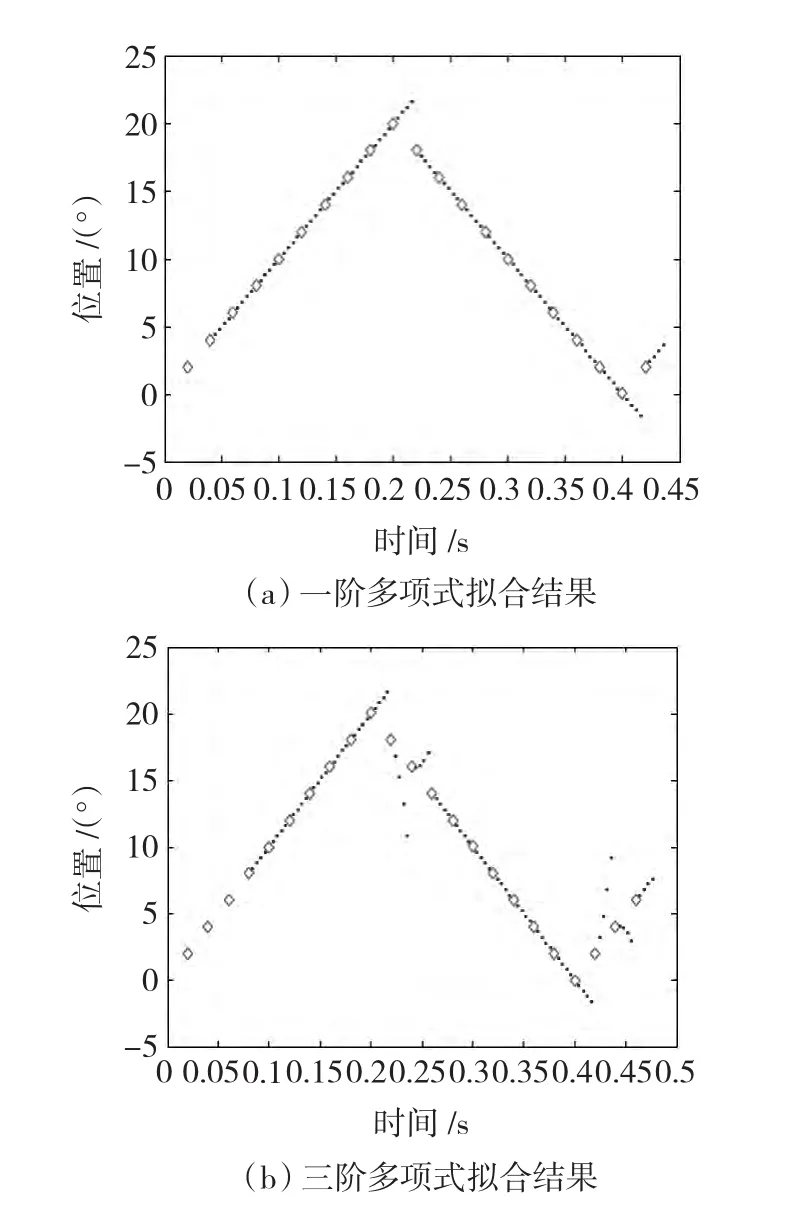
图4 不同阶次拟合多项式的三角波轨迹预测结果Fig.4 Triangle wave trajectory prediction results with different order of polynomials
图5为不同拟合函数下正弦波轨迹预测结果对比。

图5 不同阶次拟合多项式的正弦波轨迹预测结果Fig.5 Sine wave trajectory prediction results with different order of polynomials
由图5可以看出,对于正弦波的预测,若拟合函数阶次过低,在正弦尖峰处,预测效果变差。实验说明,利用最小二乘法做轨迹预测时,选择的拟合函数的阶次过高或过低,都会导致预测结果变差。对于不同类型的曲线,其拟合多项式的最佳阶次也不相同。
实际系统的目标轨迹,并不是单一的类型。由于篇幅限制,我们以正弦类轨迹与三角波类轨迹的混合轨迹作为预测目标,利用改进后的预测算法进行试验,其结构如图6所示。以下以三角波类、正弦波类混合轨迹为例,介绍这一方法。
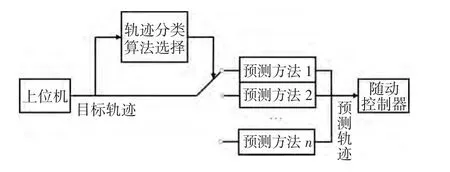
图6 改进后的预测算法流程Fig.6 Improved prediction algorithm flow
在预测开始时,首先进行轨迹分类算法选择。利用已知历史数据,采用不同阶次的多项式,进行拟合预测。若一阶多项式拟合结果误差小,则认定为三角波类轨迹;若三阶多项式拟合结果误差小,则认定为正弦波类轨迹;若二阶多项式拟合结果误差小,则认为是在两类波形之间过渡。在预测过程中,对比每个采样点处轨迹预测值与实际值之间的误差:若误差小于设定阈值,则继续采用当前预测方法;否则调整预测方法,利用其他阶次多项式拟合历史数据,将得到的预测值与实际值对比,选择误差最小的拟合方法,利用当前数据点进行预测。利用历史轨迹得到预测轨迹,并将预测结果输入随动控制器。这种加入轨迹判定的方法,比固定拟合函数的办法,预测效果更好。仿真结果如图7所示。

图7 采用不同拟合函数预测结果Fig.7 Prediction result with different order of polynomial
图7可以看出,对于不同类型的混合轨迹,采用不同拟合函数预测时,比起单一拟合函数,在不连续轨迹处,预测轨迹偏离较小;对于连续轨迹尖峰(变化较慢处),预测结果也更为准确。在仿真中只是针对此类轨迹,示意性的采用了3种不同阶次的多项式拟合函数。对于更加复杂的情况,可以采用更多不同阶次,甚至不同种类的拟合函数。
3 实际系统验证结果
实际系统的原理构成图如图1。电动机采用混合式两相步进电机。实际位置每0.5 ms采集一次(Ty=0.5 ms),位置给定每20 ms更新一次(Tr=20 ms),控制指令每2 ms更新一次(Tu=2 ms)。在不加入位置预测的情况下,系统响应如图8(a)所示(放大图中粗实线为给定值,细实线为实际轨迹),其中系统最大跟踪误差(最高点处误差)为0.081°,跟踪时延为0.035 s。

图8 系统响应曲线Fig.8 System response curve
加入了轨迹预测模块后的系统,在预测准确的情况下,等效于提高了系统的位置给定速率Tr。此时系统的响应如图8(b)所示,系统最大跟踪误差(最高点处误差)为0.0202°,跟踪时延为0.008 s。系统性能有明显提高。
4 结语
针对高精度随动控制系统中,目标轨迹给定时间间隔较大或目标轨迹不连续,造成的控制精度下降的问题,本文提出了一种利用改进最小二乘法预测轨迹,等效提升轨迹给定速率,或完善轨迹信息,从而提升系统性能的方法。通过对已知轨迹微分实现分类,并对不同类型的轨迹采用不同的预测方法。仿真证明这一方法对于系统性能的提升有较大帮助,且实现简单,无需系统模型。与传统的最小二乘法轨迹预测相比,预测结果更好。虽然对于连续不可导的轨迹,本预测方法在不可导处有较大误差。若跟踪目标具有较大惯性,其位置连续,则预测效果较好;若跟踪目标惯性较小轨迹会发生突变,则不宜采用本文提出的预测方法。
在实际应用中,跟踪目标轨迹可能还有其他类型,因此可在本文方法的基础上,加入不同的拟合函数,如选取正交多项式为基;或加入其他拟合手段,再给轨迹分类后,采用适合的办法进行预测。
[1]WELCH G,BISHOP G.An introduction to the Kalman filter[M].University of North Carolina,2001.
[2]黄晓林,杨建刚,朱雯兰.目标运动趋势预测跟踪算法及其软件实现[J].工业控制计算机,2005,18(6):42-43.
HUANG Xiaolin,YANG Jiangang,ZHU Wenlan.Trend forecasting and tracking algorithm for moving target[J].Industrial Control Computer,2005,18(6):42-43.
[3]周宏仁,敬忠良,王培德.机动目标跟踪[M].第一版.北京:国防工业出版社,1991.
[4]谭菊.基于Kalman滤波的目标轨迹预测[J].重庆文理学院学报:自然科学版,2009,28(5):28-30.
TAN Ju.Target trajectory prediction based on kalman filtering[J].Journal of Chongqing University of Arts and Science:Natural Science Edition,2009,28(5):28-30.
[5]荣盘祥,何志军.步进电机数字控制系统设计[J].电机与控制学报,2009,13(2):272-275.
RONG Panxiang,HE Zhijun.Design of numerical control system for steppermotor[J].Electric Machines and Control,2009,13(2):272-275.
[6]杨耿,和卫星.运动目标图像识别与跟踪系统的研究[J].计算机测量与控制,2005,13(3):267-269.
YANG Geng,HE Weixing.Study of system on image recognition and tracking of moving object[J].Computer Measurement and control,2005,13(3):267-269.
[7]卢迪,柳长源,闫健,等.机动目标跟踪的完全最小二乘法输入估计[J].电机与控制学报,2006,10(3):300-303.
LU Di,LIU Changyuan,YAN Jian,et al.Total least square input estimation in tracking maneuver target[J].Computer Measurement and Control,2006,10(3):300-303.

