Morlet小波解调制方法诊断鼠笼电机转子断条故障

祝洪宇， 胡静涛， 高雷， 黄昊

(1.中国科学院沈阳自动化研究所，辽宁 沈阳 110016;2.中国科学院大学，北京 100049;3.中国科学院网络化控制系统重点实验室，辽宁沈阳 110016;4.辽宁科技大学电子与信息工程学院，辽宁鞍山 114051)

0 引言

转子断条是鼠笼电机常见故障类型，约占全部故障5%～10%。早期转子断条故障诊断对提高电机运行效率、降低维护费用、减少能源浪费具有现实意义。电机电流信号特征分析(motor current signature analysis，MCSA)是诊断早期转子断条故障最常用方法［1］。根据旋转磁场理论，在假设转速恒定或转动惯量无穷大的条件下，任何转子不对称都会在定子电流频谱中引起(1－2s)fs频率成分;如果假设条件不成立，那么在电流频谱中还会出现(1+2s)fs频率成分，其中s为滑差，fs为电源基频频率。因此，在排除其他可能产生上述频率成分因素前提下，当电机稳态运行时，根据单相定子电流信号快速傅里叶变换(fast Fourier transform，FFT)频谱中是否存在转子断条故障特征频率成分fb=(1±2s)fs及幅值大小就可以判断故障发生与否及其严重程度［2］。众所周知，加窗是对信号做FFT时不可避免的处理手段，因此由加窗引起的频谱泄露是MCSA的必然结果。频谱泄露现象严重限制了MCSA方法的在线应用:在转子断条故障早期，fb非常微弱，工频供电时，fb常常为基频频谱泄露和噪声信号所堙没(当电机低负载运行时，MCSA方法甚至完全失效);当变频器供电时，为满足调速需要，电机常常在某一设定频率下稳定运行，这时fb极有可能为变频器设定频率频谱泄露所堙没，如果加之变频器高频噪声干扰的影响，故障特征识别更加困难［3－4］，目前还没有行之有效的方法处理这一问题。如何去除或削弱频谱泄露影响并抑制噪声干扰以提取故障特征频率，是进行鼠笼电机早期转子断条故障诊断的关键。

目前常用的去除或削弱频谱泄露方法包括加窗方法、滤波方法、多输入的电压和电流信号分析方法以及基于数学变换的解调制方法［1，5－8］。上述方法中，使用窗函数只是改进谱估计质量的技巧问题，而不是根本的解决办法;滤波方法和多输入电压电流信号分析方法则需要增加数据处理过程中的软硬件开销。文献［1］指出:鼠笼电机负载转矩波动、转子不对称等故障将对定子电流进行相位或幅值调制。由于调制后的电流信号包络线中包含有丰富的故障信息，因此对调制信号进行解调处理，分离提取低频包络信号，被认为是消除载波频率频谱泄露影响最直接的方法。

实现调制信号解调的关键是调制信号的包络线提取，Hilbert变换、小波变换是常用的包络线提取方法［4，9］。文献［9］对比分析了Hilbert变换和小波变换的原理、性质以及这两种数学变换在提取信号包络方面的应用，得出小波变换是较好的信号包络提取方法的结论。文献［9－10］提供了利用Morlet小波实现故障信号包络提取的严格理论证明。文献［10］进一步阐述了Morlet解析小波变换用于振动信号包络解调分析的理论基础，并以谐波组合小波诊断滚动轴承故障。文献［11］采用小波系数熵优化包络因子，提出了复平移Morlet小波包络解调方法。上述研究结果表明:由于Morlet小波变换兼具带通滤波和提取信号包络的特性，可以将噪声分解到不同的频带进行平滑，因而能够有效消除高频噪声，提高信号包络光滑度，并有利于从包络信号中找到故障特征低频频率，是非常理想的信号包络提取方法。

基于上述分析，本文提出一种基于Morlet小波解调制分析的转子断条故障诊断新方法。该方法的核心是利用Morlet小波变换的带通滤波功能以及其实部和虚部正交的特性提取故障鼠笼电机定子电流包络线，借以消除频谱泄露和噪声干扰的影响，然后对该包络线信号做FFT频谱分析，根据包络线FFT频谱中是否存在特征频率成分2sfs判断转子断条故障发生与否。区分鼠笼电机工频供电时不同负载状况以及变频器供电时不同设定频率两种情况，对所提出的方法进行了实验验证。

1 Morlet小波变换提取信号包络线原理

Morlet小波由高斯函数经余弦复调制生成，是高斯包络下的复指数函数。式(1)是Morlet小波的时域简化表述形式，该函数的傅里叶变换即频域表述形式如式(2)所示［11］。

fb，就可以改变小波形状进而优化滤波性能，从而有效去除信号中的噪声干扰。由式(1)可知，Morlet小波近似为解析小波，其虚部近似为实部的Hilbert变换。信号x(t)Morlet小波变换为

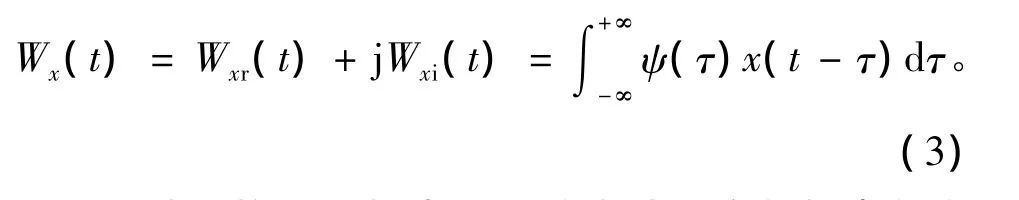
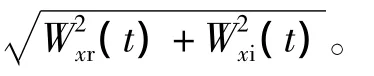
严格地说，式(1)所示的Morlet小波没有零均值，因此不满足小波允许条件，但是通过适当地选择中心频率fc和带宽参数fb的值，可以使之近似满足小波允许条件，从而将该小波视为允许小波。

2 基于Morlet小波解调制方法的转子断条故障诊断

2.1 利用Morlet小波提取故障电机定子电流包络线

根据调制理论，当鼠笼电机出现转子断条或端环断裂故障时，电流、转速、转矩都将受到周期性的扰动影响，该周期性扰动同时对定子三相电流信号ia(t)、ib(t)、ic(t)进行幅值和相位调制［12］。如果只考虑幅值调制和扰动基波分量的影响，则调制后的a相电流信号iaf(t)为

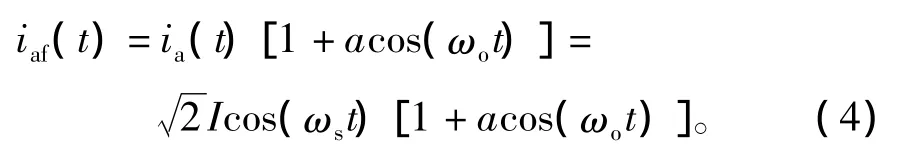
该信号的载波信号角频率即是电源供电频率ωs，调制信号角频率即周期性波动频率ωo=2πfo=2sωs=4πsfs。a代表调制深度，是一个与故障严重程度和电机负载大小有关的参数。由式(4)可知，转子断条故障特征主要包含在与周期性波动频率ωo有关的定子电流低频信息中。包络解调方法的目的是从测量信号iaf(t)中分离出这些低频信息，在此基础上诊断识别转子断条故障。

根据式(4)可以得到如式(5)所示的鼠笼电机转子断条故障a相定子电流模型，b、c两相电流模型具有对称的形式，如式(6)、式(7)所示。其中，左边频带成分fl=(1－2s)fs，右边频带成分fr=(1+2s)fs。φl和 φr分别代表左、右边频带相位角，Il和Ir分别为左、右边频带幅值，该幅值大小与调制系数a有关。

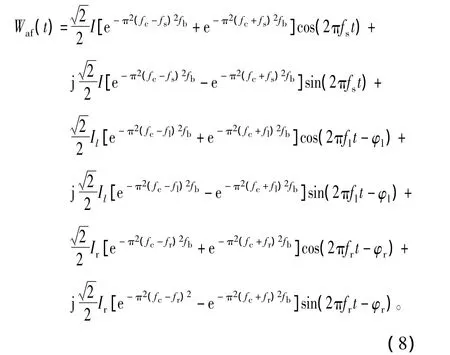
将上面提到的Morlet小波(1)与a相定子电流信号(5)做卷积，可以得到如式(8)所示的结果为选取适当的中心频率fc和带宽参数fb(如fc=fs，fb＞0.000 1)，e－π2(fc+fs)2fb、e－π2(fc+fl)2fb、e－π2(fc+fr)2fb

可忽略不计，于是得到简化表达形式为

将式(9)的实部与虚部进行平方合成，获得故障电流信号iaf(t)的包络线|Waf(t)|为

由上述推导可知:通过选择合适的中心频率fc和小波参数fb，就可以在提取故障信号包络线过程中将基频分量转化成直流分量，从而消除基频频谱泄露对故障特征成分的影响，并且有效抑制与转子断条故障特征频率无关的其他频率成分。在MCSA方法中，转子断条故障特征频率为fb=(1±2s)fs。但是在包络线频谱中，故障特征频率为单一的谱线2sfs和4sfs。鉴于2sfs的幅值要远大于4sfs的幅值，所以选择2sfs作为故障特征频率。该频率成分的出现直接反映了转子断条故障，且其幅值随着故障严重程度和负载增大而增大。由于不受基频频谱泄露影响，该特征频率更易于识别。

理论与实践表明［1］，当鼠笼电机发生转子断条故障时，定子电流中将出现故障特征频率fb=(1±2s)fs。该公式提供了小波参数fc和fb的选择依据。例如，鼠笼电机工频供电、额定转速以下运行时，转子滑差一般在0.05～0之间变化，断条故障特征频率成分fb∈［45 Hz，55 Hz］。这时如果选择小波参数fc=fs，带宽参数fb≥0.01，就可以获得满意的滤波效果，并在提取包络线过程中消除基频fs频谱泄露的影响。变频器供电时，为满足调速需要，供电频率经常根据负载变化而变化。这时，故障特征频率分布与变频器设定频率周围，只要根据变频器设定频率的变化情况适时调整中心频率fc和参数fb的取值范围，同样能取得很好的滤波效果。

2.2 转子断条故障诊断方法

根据上述分析，提出一种基于Morlet小波变换解调制分析的鼠笼电机转子断条故障诊断方法，该方法功能框图如图1所示。

图1 故障诊断功能框图Fig.1 Functional diagram of fault diagnosis methods

3 实验及结果分析

3.1 实验装置及实验过程

实验装置由电源系统、电机拖动系统、数据采集系统、数据处理中心4部分组成。电源系统包括西门子变频器和50 Hz工频电源，通过转换开关实现变频和工频两种供电方式切换。电机拖动系统包括实验电机和直流发电机负载。数据采集系统由电流互感器、自制调理电路、数据采集卡组成，采集卡信号输入方式设定为差分输入，输入电压范围为±10 V。实验电机是2台额定功率3 kW、额定电压380 V、额定电流6.8 A的鼠笼电机，其中1台电机无故障，用作实验参照，另1台电机带有1根断条故障，用于方法验证。电机实验台和实验用故障转子如图2所示。

图2 电机实验台和实验用故障转子Fig.2 Experiment setup and broken rotor used in the tests

在工频和变频器供电条件下对无故障电机和故障电机进行测试。工频供电时，使电机在25%、50%、75%、91%额定负载下稳定运行，以此验证该方法在不同负载情况下提取转子断条故障特征频率的稳定性;变频器供电时，变频器设定频率为32 Hz、45 Hz，以此验证该方法在不同供电方式下提取故障特征频率的有效性和抑制噪声的能力。实验过程中，数据采样时间10 s、采样频率为4 kHz。在Matlab7.0环境下对测得的数据做离线分析，频谱图纵坐标采用对数分度，所有数据以基频分量幅值为基准做归一化处理。表1所示为电机测试状态和相应的故障特征频率理论值。

表1 电机故障特征边频带理论值Table 1 Theoretical fault sidebands of healthy and faulty motor

3.2 实验结果分析

图3为工频供电无故障鼠笼电机定子电流FFT频谱和经过Morlet小波解调制处理后的包络线FFT频谱。由于图中没有出现转子断条故障特征频率fb=(1±2s)fs(图3(a))或fb=2sfs(图3(b))，因此表明该电机无故障。

图3 工频供电无故障鼠笼电机定子电流FFT频谱和包络线频谱Fig.3 FFT and Envelope spectrum of motor stator current for main-fed healthy squirrel cage motor

图4所示为工频供电故障鼠笼电机定子电流FFT谱。对比图3(a)，从图4中可以清楚地看出基频频谱泄露对转子断条故障特征频率fb=(1±2s)fs的影响:鼠笼电机在50%额定负载下工作时，采用MCSA方法能够清晰识别出转子断条，这时，左边频带特征为(47.2 Hz，－40 dB)，右边频带特征为(52.8 Hz，－41 dB);当电机负载降至25%额定负载时，故障特征频率fb完全被基频频谱泄露所堙没，采用MCSA方法已经无法诊断出转子断条故障。

图4 工频供电故障鼠笼电机定子电流FFT频谱Fig.4 FFT spectrum of motor stator current for main-fed fault squirrel cage motor

图5 工频供电故障电机定子电流包络线频谱Fig.5 Envelope spectrum of motor stator current for main-fed fault squirrel cage motor

由图5可见:由于在提取包络线过程中基频成分转化成了直流分量，因此包络线频谱中的转子断条故障特征频率2sfs不受基频频谱泄漏现象的影响，而且随着负载增大，故障特征频率2sfs幅值逐渐增大，这与理论推导显示的结果是一致的。从图5(a)中还看出:即使当电机在25%的低负载情况下运行时，采用所提出的算法仍然能清晰地识别出2sfs特征成分，从而表明该算法比对定子电流直接做FFT分析具有明显的优势。

图6是变频器不同设定频率下故障鼠笼电机定子电流包络线细化频谱，图中标注代表转子断条故障特征2sfs的频率值和归一化幅值。比较图6与图5可见，当鼠笼电机由变频器供电时，包络线FFT频谱中的谐波成分明显增多，这增加了故障特征识别难度。但是，对比图6和图3(b)可知，采用本文提出的诊断方法能够有效抑制噪声干扰，并清晰地识别出转子断条故障特征频率2sfs。图6中，故障特征频率2sfs在频谱中的位置随着变频器设定频率fs的变化而变化。

图6 变频器供电故障电机定子电流包络线频谱Fig.6 Envelope spectrum of motor stator current for inverter-fed fault squirrel cage motor

4 结语

基频频谱泄露现象严重限制了MCSA方法的在线应用，本文提出一种基于Morlet小波解调制分析的鼠笼电机转子断条故障诊断方法解决这一问题。该方法利用Morlet小波的带通滤波功能和其实部和虚部正交的特性提取故障定子电流信号包络线，并对该包络线做FFT分析，根据FFT频谱中是否存在特征频率成分2sfs判断转子断条故障发生与否。通过适当选取适当小波中心颇率fc和带宽fb，使滤波器覆盖信号中与故障特征有关的频带，借以提取出较理想的包络，有效消除了频谱泄露的影响。理论分析与实验结果表明，当鼠笼电机在工频供电不同负载以及变频供电不同设定频率下稳定运行时，所提出的方法能有效提取出故障特征频率并对早期转子断条故障进行诊断识别。

［1］MEHRJOU M R，MARIUN N，et al.Rotor fault condition monitoring techniques for squirrel-cage induction machine-A review［J］.Mechanical Systems and Signal Processing，2011，25(8):2827－2848.

［2］FILIPPETTI F，FRANCESCHINI G，et al.AI techniques in induction machines diagnosis including the speed ripple effect［J］.IEEE Transactions on Industry Applications，1998，34(1):98－108.

［3］侯新国，卜乐平，邵英.带变频驱动系统的感应电机故障诊断研究［J］.电机与控制学报，2011，15(8):23－28.

HOU Xinguo，BU Leping，SHAO Ying.Research on faults diagnosis methods of induction motors with variable frequency driver system［J］.Electric Machines and Control，2011，15(8):23－28.

［4］张雄希，刘振兴.共振解调与小波降噪在电机故障诊断中的应用［J］.电机与控制学报，2010，14(6):66－70.

ZHANG Xiongxi，LIU Zhenxing.Application of resonance demodulation and wavelet denosing in fault diagnosis of induction motors［J］.Electric Machines and Control，2010，14(6):66－70.

［5］阳同光，蒋新华，付强.瞬时功率频谱分析在牵引电机转子

故障诊断的应用研究［J］.电机与控制学报，2012，16(10):95－99.

YANG Tongguang，JIANG Xinhua，FU Qiang.Study on application of spectral analysis of instantaneous power to fault diagnosis of traction motor rotor［J］.Electric Machines and Control，2012，16(10):95－99.

［6］马宏忠，姚华阳，黎华敏.基于Hilbert模量频谱分析的异步电机转子断条故障研究［J］.电机与控制学报，2009，13(3):371－376.

MA Hongzhong，YAO Huayang，LI Huamin.Study on rotor broken-bar fault in induction motors based on spectrum analysis of Hilbert modulus［J］.Electric Machines and Control，2009，13(3):371－376.

［7］安国庆，刘教民，郭立炜，等.利用相关性基波消去法诊断电机转子断条故障［J］.电机与控制学报，2011，15(3):69－73.

AN Guoqing，LIU Jiaomin，GUO Liwei，et al.Diagnosing rotor broken bar fault in motor by using correlation fundamental component filtering method［J］.Electric Machines and Control，2011，15(3):69－73.

［8］谢国民，王灿祥，佟莹.采煤机电动机故障诊断专家系统的研究与应用［J］.信息与控制，2013，42(3):358－363.

XIE Guomin，WANG Chanxiang，TONG Ying.Research and application of expert system on fault diagnosis of shearer motor［J］.Information and Control，2013，42(3):358－363.

［9］张绪省，朱贻盛，成晓雄，等.信号包络提取方法－从希尔伯特变换到小波变换［J］.电子科学学刊，1997，19(1):120－123.

ZHANG Xusheng，ZHU Yisheng，CHENG Xiaoxiong，et al.The methods of extracting signal envelop-from Hilbert transform to wavelet transform［J］.Jounal ofelect ronics，1997，19(1):120－123.

［10］张家凡，易启伟，李季.复解析小波变换与振动信号包络解调分析［J］.振动与冲击，2010，29(9):93－96.

ZHANG Jiafan，YI Qiwei，LI Ji.Complex analytic wavelet transform and vibration signals envelope-demodulation analysis［J］.Journal of Vibration and Shock，2010，29(9):93－96.

［11］NIKOLAOU N G，ANTONIADIS I A.Demodulation of vibration signals generated by deffects in rolling element bearings using complex shifted morlet wavelets［J］.Mechanical Systems and Signal Processing，2002，16(4):677－694.

［12］TRZYNADLOWSKI A M，RITCHIE E.Comparative investigation of diagnostic media for induction motors:a case of rotor cage faults［J］.IEEE Transactions on Industrial Electronics，2000，47(5):1092－1099.