采用载波移相技术永磁电机高频振动抑制研究

袁飞雄， 黄声华， 郝清亮

(1.华中科技大学电气与电子工程学院，湖北武汉 430074;2.武汉船用电力推进装置研究所，湖北武汉 430064)

0 引言

现代电力驱动中，振动噪声越来越引起关注。尤其在PWM逆变器供电电机中，逆变器输出基频电压及开关过程导致时间谐波都能激发起电机振动噪声。文献［1－6］分析PWM逆变器供电电机电磁激振力及振动噪声理论模型。文献［1－2］提出感应电机电磁激振力及振动噪声模型，分析感应电机振动特征，如主要激振力，电机自然频率和谐振频率。文献［2］提出采用变开关频率方式，避免电磁激振力引起的电机谐振，从而达到降低电机振动噪声目的。

文献［2］和文献［6］分析电机模型及电磁激振力频谱，提出选择合适载波频率以避免谐振，该方法能够有效降低电机振动噪声。但计算电机高频谐振频率比较困难，限制了该方法应用。文献［5］提出一种新方法实现声学噪声闭环控制，该方法采用连续调节V/f获得恒定转矩同时，动态调整功率器件开关频率避免谐振。但是该方法需要测量声学噪声实现闭环调节，对噪声测量要求高，鲁棒性差。

随机脉宽调制方法被用于减小电机电磁噪声［7－9］，该方法在一定范围内平缓噪声频谱中尖峰，将能量平均分配在整个随机频带内。文献［10－11］提出采用特定谐波消除技术抑制噪声。在1/3倍频程振动加速度测量中，这些方法对于振动噪声改进效果有限。文献［12］提出采用特殊设计电机及PWM逆变器，通过调节逆变器开关频率，使得电机齿槽频率与PWM逆变器导致磁动势频率一致，相互削弱来降低电机振动噪声。该方法需要对电机及变频器进行特殊设计，限制其应用范围。

电磁振动噪声特性取决于径向磁场力及电机机械模型。省略了电机机械模型复杂理论推导，本文重点研究电机电磁激振力，通过分析气隙中径向磁压力变化来研究电机振动噪声特性。在理论分析基础上，提出采用载波移相技术，在两台PWM逆变器间，载波移动适当的角度去消除气隙磁动势谐波，达到降低高频振动噪声目的。仿真分析及实验结果表明，采用该方法之后，在对应的边频带，高频振动加速度能降低18 dB。

1 双PWM逆变器供电永磁同步电机模型

作为多相电机优点之一，在采用相同规格功率器件条件下，多相电机驱动系统能够实现更大的功率输出。尤其是在电力船舶推进，轨道交通，风力发电等领域，多相电机被广泛应用。在多相电机驱动系统中，应用最广泛的为双三相电机(dual threephase motor)，与一般三相电机不同，这种电机定子绕组采用中点隔离空间相移30°电角度的两套三相绕组。双三相电机一般采用两台普通三相电压源逆变器供电，形成六相驱动系统。

为了增加额定电流，也可以采用另外一种方式。与双三相电机不同，定子绕组也可以采用多个中点电位隔离同相位三相绕组。本文中电机采用两个中点相互隔离的三相绕组，两个三相绕组在定子中采用同槽结构，分别由两台三相逆变器供电，如图1所示。

图1 双PWM逆变器供电三相永磁同步电机Fig.1 Proposed PMSM fed by dual PWM inverters

虽然定子采用两套三相绕组，该永磁同步电机依然为三相电机，电磁及振动噪声模型与文献［1－2］所描述电机本质上一致。本文对其机械特性不进行详细推导，重点讨论PWM逆变器引入高次谐波对振动影响。

2 振动电磁激振力

电机机械模型及径向磁场力决定了电机振动和噪声特性。径向磁场力作用于定子效果可以用气隙中压力分布描述。文献［1］和文献［13］给出了径向压力PM的近似表达式为

式中:Bg为气隙径向磁感应强度分量;μ0为真空中磁导率;气隙径向磁场强度分量Bg可以表示为磁导与磁动势乘积［1］，即

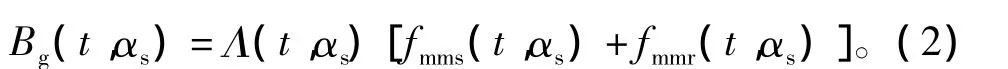
式中:αs为空间位置角;Λ=μ0/ge为单位面积磁导;ge为等效气隙长度;fmms、fmmr分别为定、转子磁动势。

考虑变频供电时，由于PWM调制引入谐波电流，电机定子绕组磁动势可以表示为

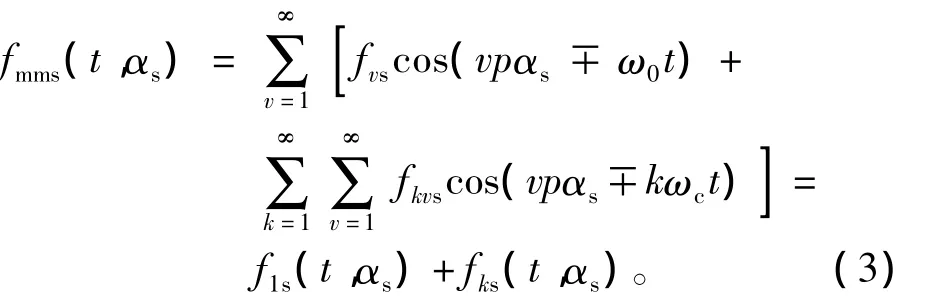
式中:p为极对数，方程第一项表示由基波电流产生磁动势波，第二项表示由于PWM调制引入谐波电流产生磁动势波。

忽略磁槽效应，假定气隙均匀，定子绕组为理想绕组，气隙中主要径向磁场力可表示为

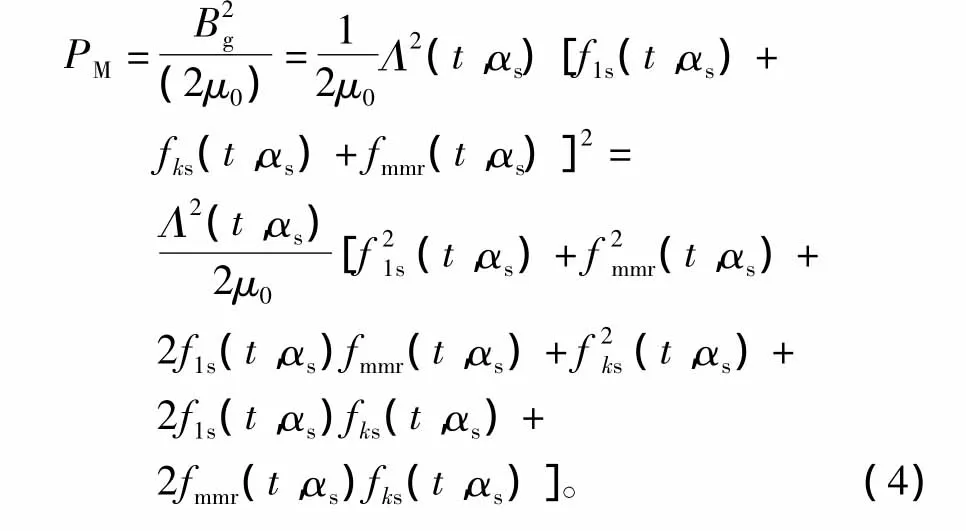
式中:第一、二项分别表示由基波电流及转子磁钢产生径向电磁力;第三项表示基波电流及转子磁钢相互作用产生电磁力;第四项表示由PWM调制引入谐波相互作用导致电磁力;剩余两项分别表示PWM调制引入谐波与基波电流及转子磁钢相互作用导致电磁力。

PWM逆变器供电电机，由于功率器件开通与关断，定子绕组中必定含有开关频率及其倍频边频带谐波电流。这些高频谐波电流产生磁动势，影响气隙中磁场分布，必然导致电机高频振动噪声。如果能够降低这些高频谐波电流，必然能减小磁动势中谐波分量，从而降低由PWM调制引入的高频振动噪声。

3 载波移相方法

PWM调制技术为电力电子领域基本技术之一被广泛应用，其中自然规则采样的PWM比较常见。该方法采用正弦参考波与三角载波信号进行比较。得到开关器件控制信号。在如图1所示的三相逆变器中，频率为ω0正弦参考波与频率为ωc三角载波比较，得到开关器件导通关断控制信号。逆变器1输出线电压可以表示为［14］式中:M为调制比;Jn为n阶贝塞尔函数;Vdc为直流母线电压。图2为采用自然规则采样的PWM调制输出线电压谐波随调制比变化曲线。在低调制比时，2fc±f0频率的谐波分量最大，随着调制比升高，fc±2f0逐渐增大。

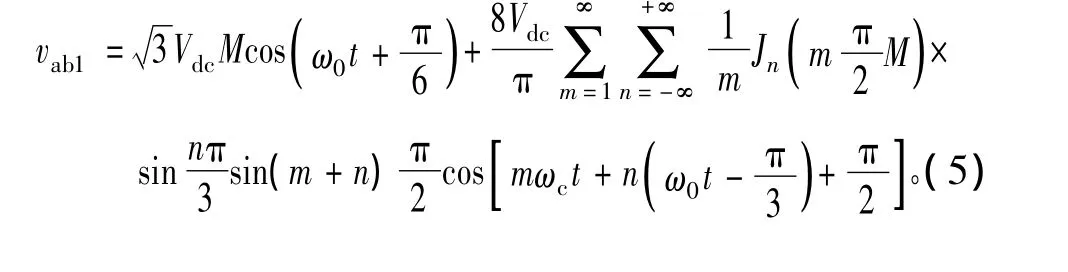
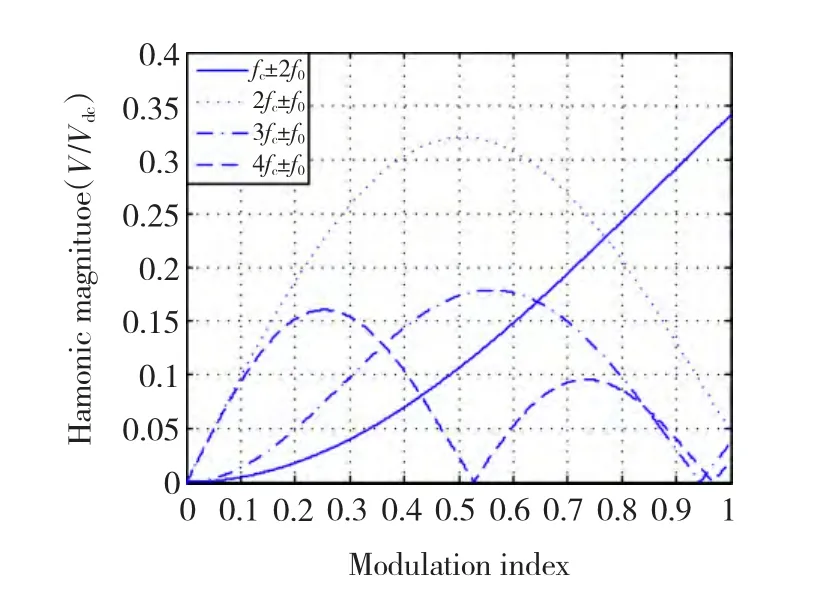
图2 SPWM调制谐波随调制比变化曲线Fig.2 Evolution of natural sampling PWM voltage harmonic as function of the modulation index

PWM逆变器产生高频谐波电压注入电机定子绕组后，必然产生同频率的谐波电流。为简化推导，将a1相谐波电流初始相位设定为0，定子绕组中电流可以表示为

式中:I1为基波电流幅值，Imn为m边频带的第n次谐波电流幅值。其余两相电流可以通过以上a相电流依次移动2π/3电角度得到。只考虑各电流产生同次磁动势，忽略谐波磁动势，以上三相电流产生磁动势可以表示为

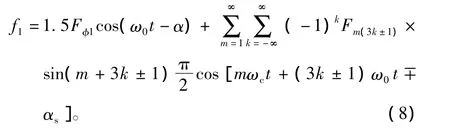
式中:Fφ1为相基波磁动势幅值;Fm(3k±1)为谐波电流磁动势幅值;αs为空间角位置，具体推导过程参考文献［13］。

采用载波移相技术，逆变器2注入到电机定子绕组的电流及磁动势可以表示为

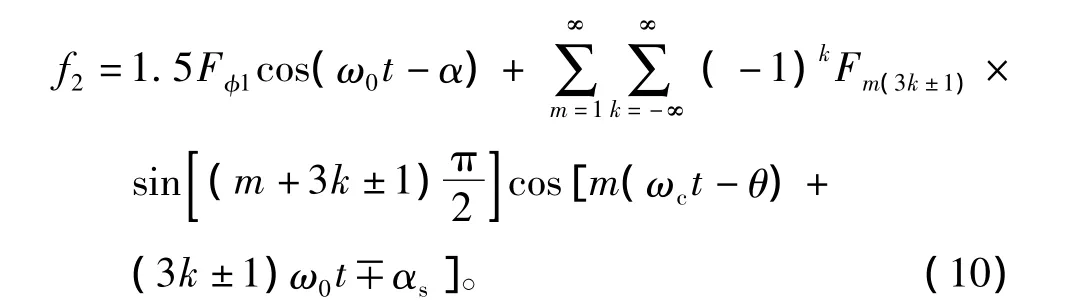
如图1所示双PWM逆变器供电电机，总的定子磁动势为

式(11)第一项表示基波电流产生基波磁动势，后面两项表示谐波电流产生同次空间谐波磁动势。可以推导，对于双三相电机，磁动势表达式与式(11)相似，只是由于绕组空间布置不一致，多了绕组系数。载波移相角与合成磁动势关系与式(11)一致。因此，本文提出方法，可以推广到多相电机中。

如果mθ=(2l+1)π，则磁动势中对应的m=(2l+1)π/θ次谐波相互抵消。如果令第二个逆变器与第一个逆变器三角载波相位角为θ=π/2，则m=4l+2的边频带的所有各次谐波都相互抵消。同样，如果θ=π则所有m为奇数的边频带所有谐波磁动势被抵消掉。

采用载波移相技术，通过适当调整两台逆变器载波相位，可以将某些边频带谐波相互抵消，降低气隙中谐波磁动势，从而达到降低振动噪声目的。

4 仿真分析

按照图1所示的拓扑结构，进行电流仿真。自然采样PWM中，三角载波频率2 500 Hz，调制波频率为50 Hz，调制比为0.5，分别对载波移相角π/2和π进行仿真。为了保持相电流幅值一致性，将逆变器1输出电流ia1，逆变器2输出电流ia2及总电流一半(ia1+ia2)/2进行对比分析，仿真结果如图3、图4所示。

载波移相角θ=π/2时，各逆变器m=4l+2的边频带各次谐波电流大小一致，角度相差π，因而在总电流中相互抵消，不存在该频带的各次谐波电流。同样，载波移相角θ=π时，总电流中不包含所有奇数次变频带的各次谐波电流。仿真结果与理论推导一致。

两台逆变器之间载波相位调整合适的角度，在总电流中能消除某些边频带所有谐波。电流引起的磁动势对应频率的谐波也不存在，达到抑制对应频率的高次振动目的。

图3 π/2载波移相角时电流频谱(从上自下依次为(ia1+ia2)/2，ia1和ia2)Fig.3 The current spectra with π/2 phase shifted carrier(from top to bottom:(ia1+ia2)/2，ia1and ia2)

图4 π载波移相角时电流频谱(从上自下依次为(ia1+ia2)/2，ia1和ia2)Fig.4 The current spectra with π phase shifted carrier(from top to bottom:(ia1+ia2)/2，ia1and ia2)

5 试验结果

在一台额定功率为600 kW，额定转速为240 r·min－1的永磁同步电机实验平台上进行实验。两台逆变器为同型号普通三相桥逆变器，采用载波频率为2 500 Hz的自然规则采样PWM调制。电流测量采用配备泰克A621电流探头的DPO 4032示波器，振动检测装置采用B＆K 3560D型噪声振动多分析系统。

两台逆变器之间载波移相角分别为0、π/2和π时，对总电流进行频谱分析，试验结果如图5所示。与不移相相比，移相角度为π/2的总电流不包含m=4l+2的边频带的谐波电流;移相角度为π的总电流中不包含所有奇数次边频带的谐波电流。振动加速度显著降低。试验结果表明，载波移相对相应边频带的高频振动有明显的抑制作用，抑制效果不会随转速变化减弱，并且不会影响其他的边频带的高频振动。

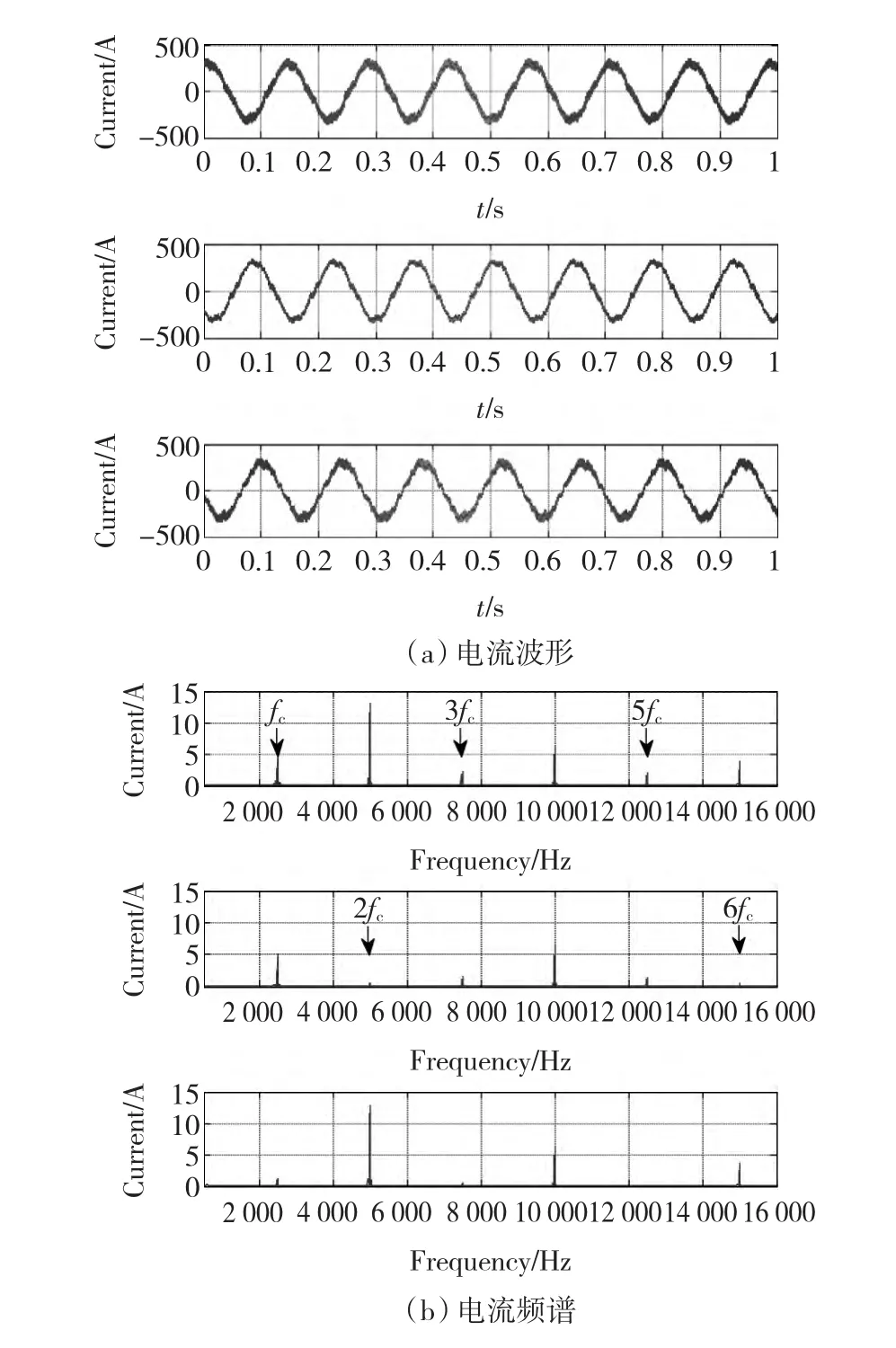
图5 载波移相总电流(ia1+ia2)/2及频谱(从上至下移相角分别为0，π/2和 π)Fig.5 The currents and spectra of(ia1+ia2)/2 with carrier phase shifted(from top to bottom:0，π/2 and π)

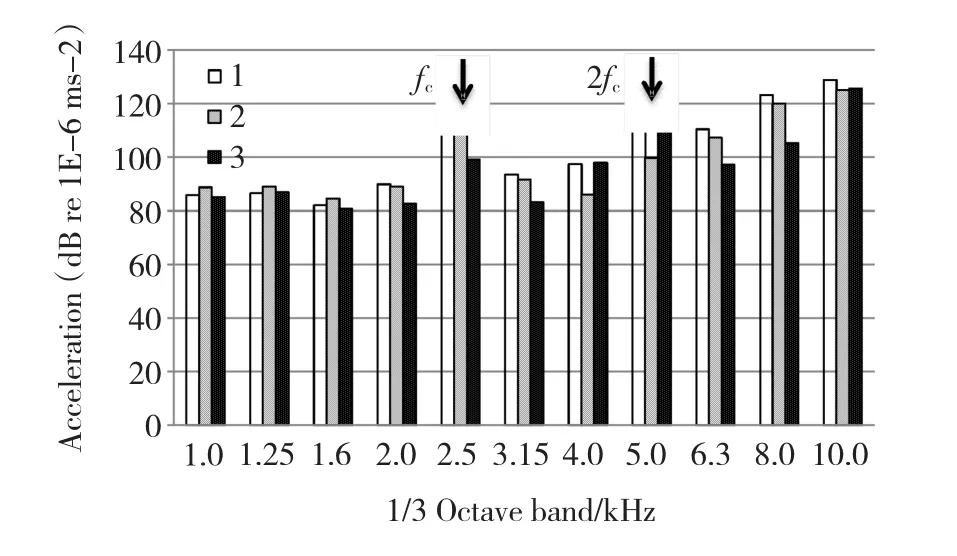
图6240 r/min振动加速度频谱(1，2，3分别为载波移相角为0，π/2和π)Fig.6 The spectra of vibration acceleration under 1/3 octave band at 240 r/min with 0.6 modulation index without load(1:0 phase shifted，2:π/2 phase shifted，3:π phase shifted)

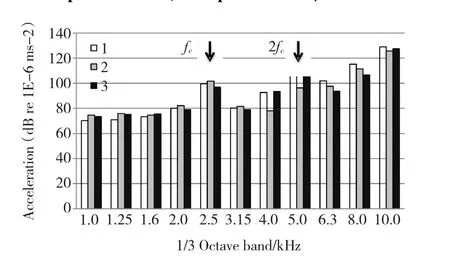
图7120 r/min振动加速度频谱(1，2，3分别为载波移相角为0，π/2和π)Fig.7 The spectra of vibration acceleration under 1/3 octave band at 120 r/min with 0.3 modulation index without load(1:0 phase shifted，2:π/2 phase shifted，3:π phase shifted)

图8 电机转速变化5 000 Hz中心频率处振动加速度(1，2分别为载波移相角为π/2和π)Fig.8 The decline of vibration acceleration compared with 0 phase shifted without load(1:π/2 phase shifted at 5 000 Hz，2:π phase shifted at 2 500 Hz)

6 结语

本文提出载波移相技术抑制双PWM逆变器供电的永磁同步电机高频振动。通过调整两台逆变器载波之间相位角度，使得两台逆变器输出电流中相应边频带谐波相位角变化，削弱气隙磁动势中的对应频率谐波，达到降低电机高频振动目的。两台变频器载波移相角度为π/2时，能够将中心频率为5 000 Hz的高频振动降低18 dB。仿真及实验数据验证该方法有效性。根据理论推导，该方法能够应用到多相电机驱动系统中，对多相电机高频振动起到明显抑制作用。

［1］BESNERIAS J L，LANFRANCHI V，HECQUET M，et al.Prediction of audible magnetic noise radiated by adjustable-speed drive induction machines［J］.IEEE Transactions on Industry Appilationl，2010，46(4):1367－1373.

［2］BESNERIAS J L，LANFRANCHI V，HECQUET M，et al.Characterization and reduction of audible magnetic noise due to PWM supply in induction machines［J］.IEEE Transactions on Industrial Electronics，2010，57(4):1288－1295.

［3］PELLEREY P，LANFRANCHI V，FRIEDRICH G.Coupled numerical simulation between electromagnetic and structural models.Influence of the supply harmonics for synchronous machine vibrations［J］.IEEE Transactions on Magnetic，2012，48(2):983－986.

［4］VERDYCK D，RONNIE J M.An acoustic model for a permanent magnet machine:modal shapes and magnetic forces［J］.IEEE Transactions on Industrial Electronics，2012，59(3):1346－1354.

［5］TORREGROSSA D，PAIRE D，PEYRAUT F，et al.Active mitigation of electromagnetic vibration radiated by PMSM in fractional－horsepower drives by optimal choice of the carrier frequency［J］.IEEE Transactions on Industrial Electronics，2012，59(3):1346－1354.

［6］HASHEMI N，LISNER R，HOLMES D G.Acoustic noise reduction for an inverter-fed three-phase induction motor［C］//IEEE Industrial Applocations Society Annual Meeting Conference，Oct.3－7，2004，Seattle，WA.2004:2030－2035.

［7］TRZYNADLOWSKI A M.Active attenuation of electromagnetic noise in an inverter-fed automotive electric drive system［J］.IEEE Transactions on Power Electronics，2006，21(3):693－700.

［8］CHAI J Y，HO Y H，CHANG Y C，et al.On acoustic noise reduction control using random switching technique for switch mode rectifiers in PMSM drive［J］.IEEE Transactions on Industrial E-lectronics，2008，55(3):1295－1309.

［9］BORISOV K，CALVERT T E，KLEPPE J A，et al.Experimental investigation of a naval propulsion drive model with the PWM-based attenuation of the acoustic and electromagnetic noise［J］.IEEE Transactions on Industrial Electronics，2006，53(2):450－457.

［10］AGELIDIS V G，BALOUKTSIS A I，DAHIDAH M S A.A fivelevel symmetrically defined selective harmonic elimination PWM stratege:Analysis and experimental validation［J］.IEEE Transactions on Power Electronics，2008，23(1):19－26.

［11］AGELIDIS V G，DAHIDAH M S A.Selective harmonic elimination PWM control for cascaded multilevel voltage source converters:A generalized formula［J］.IEEE Transactions on Power E-lectronics，2008，23(4):1620－1630.

［12］BESNERAIS J L，BAROEUL M.Vibration and noise control strategy in electrical machines［P］.US:2011/0215745 A1，2011－09－08.

［13］TIMAR P.Noise and vibration of electrical machines［M］.Elsever，1989.

［14］HOLMES G，LIPO T A.Pulse width modulation for power con

verters principles and practice［M］.Hoboken，NJ:Wiley，2003.