带阻抗观测器的单相逆变器抗扰控制

闫士杰， 闫伟航， 冷冰， 陈宏志

(东北大学信息科学与工程学院，辽宁沈阳 110819)

0 引言

近年来，随着太阳能发电的快速发展，作为功率接口的多种功能逆变器得到了广泛应用［1－10］。应用于太阳能发电系统的单相逆变器分为并网逆变器和离网逆变器。由于用途不同，导致两种逆变器的控制方法也完全不同。并网逆变器一般采用正弦脉冲宽度调制(sinusoidal pulse width modulation，SPWM)的电流控制方式，使注入电网的电流谐波含量小，且尽量控制电流与电网电压同相位［3－6］。离网逆变器由于不涉及并网问题，所以没有电压的相位控制问题，一般采用有效值控制法和幅值控制法［7－9］。为了便于光伏逆变器的多功能应用，多采用并网和离网相结合的模式，即双模式控制方法［10］。在并网模式下，逆变器系统在电流控制的同时，也要进行电网电压锁相控制。在离网模式下，为了保证逆变器输出电压为完美正弦波，也必须对逆变器输出电压和相位进行控制。这两种模式的控制方法实质都是对电压波形的跟踪控制:并网模式是对电网电压波形的跟踪，离网模式是对给定电压波形的跟踪。如果将给定电压波形设定为电网波形，则两种模式的控制就可统一为一种波形跟踪控制。目前，对光伏逆变器输出波形实现跟踪控制是非常困难的，主要原因:一是由于太阳能发电具有很大的随机性，导致逆变器的输出电压波形波动频繁。二是由于逆变器容量有限，非线性负载的接入会导致逆变器输出波形产生畸变。三是由于温度变化、线路和滤波器的阻抗参数变化、检测电路的延迟等，会导致系统检测信号存在误差，从而引起输出电压变化。如果我们将引起电压波动的上述原因都视为一种干扰，就可应用抗扰控制器来解决这些问题，保证逆变器输出电压波形对给定电压波形的完美跟踪。

抗扰控制器自韩京清先生1998年提出以来，得到了广泛应用［11－13］，但在逆变器控制系统上应用却很少。主要由于抗扰控制系统中需要定义的参数太多，而逆变器控制系统又是一种快速系统，所以导致实际应用过程中无法快速准确设定参数，控制效果不甚理想。本文在系统分析了抗扰控制器的控制机理基础上，通过构造一个阻抗观测器，来校正抗扰控制器中的参数。这样，扩张状态观测器(extended state observer，ESO)就能够实时准确地跟踪系统的各阶状态变量，对外部扰动进行快速补偿，从而使控制系统能够缩短误差衰减时间，加快系统收敛速度，有效地抑制稳态误差，达到消除逆变器输出谐波，补偿逆变器输出电压畸变的目的。

1 系统建模

单相逆变器主电路和控制系统结构如图1所示。在主电路中，S1～S4为IGBT功率开关;C1为直流侧电容;C2为交流滤波电容;L为交流滤波电感;R为负载电阻;PWM1～PWM4为IGBT驱动信号;Ud为主电路直流电压;V为单相逆变器的输出电压;iR为单相逆变器负载侧电流。在控制框图中，r为参考信号，u为控制器输出信号。

图1 单相逆变器电路和控制系统框图Fig.1 Single-phase inverter circuit and control system diagram

系统控制目标:应用阻抗观测器的输出，修改控制器参数，在直流侧电压波动、负载突变和非线性负载接入等情况下使逆变器的输出电压V紧紧跟随给定的正弦电压r的变化，保证逆变器输出电压总谐波畸变率(total harmonic distortion，THD)最小。根据图1可知，设PWM生成器工作在线性区，在不考虑控制器的情况下，以u为输入，V为输出，则稳态情况下单相逆变器在S域的输出电压和输出电流为

将式(2)代入式(1)后，得逆变器稳态运行时的传递函数为

将式(3)转换为微分方程的形式后为

式(4)为系统稳态时的数学模型。

在太阳能发电系统中，由于天气变化和气候变换等因素的影响，导致光伏逆变器直流侧会存在很大的扰动。同时，逆变电源由于输出侧谐波、容抗、感抗、线路参数变化、功率因数变化、滤波器和线路的时延、控制检测电路的时延、温度变化等，也使系统输出存在很大的扰动。另外，逆变电源带非线性负载时，也会引起系统扰动。如果将这些扰动变量设为w，则可定义含各种扰动量的函数为

将式(5)代入式(4)中，则可得到系统在扰动情况下的数学模型为

式中:w为来自系统各种因素引起的干扰;b=1/LC为系统控制参数;f为含有逆变器控制系统内扰和外扰综合特性的函数。

2 抗扰控制器构成

根据抗扰控制器的系统结构［11］，考虑到实现电压快速跟踪的目的，应用数学模型式(6)，建立一个适于逆变器的二阶抗扰控制系统。图2为逆变器控制系统框图。

图2 逆变器控制系统框图Fig.2 Control block diagram of inverter control system

在图2中，各变量和参数含义如下:r为逆变器控制系统的给定;V为逆变器控制系统的输出;G(s)为逆变器传递函数;u1为控制器TC1的输出;u2为控制器TC2的输出;u为控制器TC3的输出;y1为ESO的输出;y2为ESO的输出;y3为ESO的输出;w为系统外部的干扰。

在系统中，扩张观测器ESO定义为［13］

其中:k1、k2、k3为ESO观测器参数;b0为b的估计值。为了保证快速跟踪，设控制器TC1为比例控制器，其参数为kp;TC2为微分控制器，其参数为kd;TC3为前馈控制器，其参数为1/b0。由此可得控制系统输出为

当ESO能够实现y1很好地跟踪V，且y2很好地跟踪时，y3很好地跟踪式(6)中的f时，则从式(7)可得

将式(9)代入式(8)后，则系统闭环传递函数为

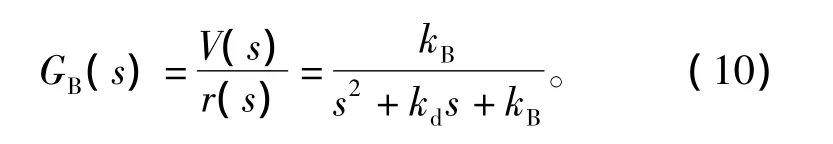
式中，kB=kpkd。

由式(10)可以看出，只要ESO按照式(7)的形式定义，则逆变器的传递函数都可通过抗扰控制器来逼近成为一个标准的二阶传递函数。

事实上，在频域内，式(7)可变换为

根据式(11)可知，图2中的实际系统闭环传递函数为

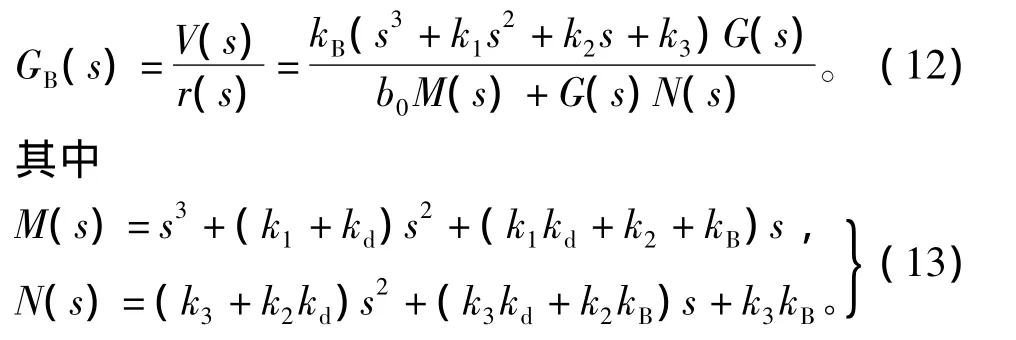
对式(12)的闭环传递函数进行等效变换［14］。令

将式(14)代入式(12)，则系统闭环传递函数可简化为

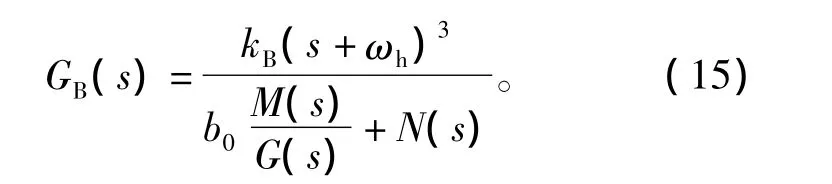
式(10)和式(15)均为图2控制系统闭环传递函数，当ESO成功实现时，两式应逼近为相同形式。两式对比后，有

将式(17)变换为［14］

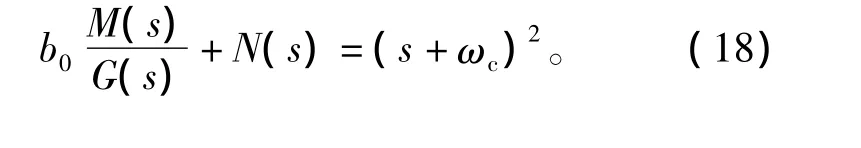
其中:ωc为系统截止频率;ωh为观测器带宽。

从式(16)和式(18)可以看出，只要整定ωc和ωh，就可确定系统闭环传递函数式(12)。

由式(17)和式(18)可得

由式(14)可得

由于k1、k2和k3是直接影响ESO观测器精确度的参数，且逆变器控制系统为快速系统，所以ωh一般不能过大，否则会造成系统不稳定。本文参照文献［11］，取ωh的初始值为控制系统截止频率的2倍，然后再通过阻抗观测器进行自动校正。

将式(3)变换为标准传递函数形式

则 ωn和 ξ为

根据控制系统截止频率的定义，对于式(21)，当ω=ωc时，则G(s)的模A(ωc)=1。将其代入式(21)，则有

将式(22)代入式(23)中，可得

将式(24)代入式(19)中，可得

将式(24)代入式(20)中，可得

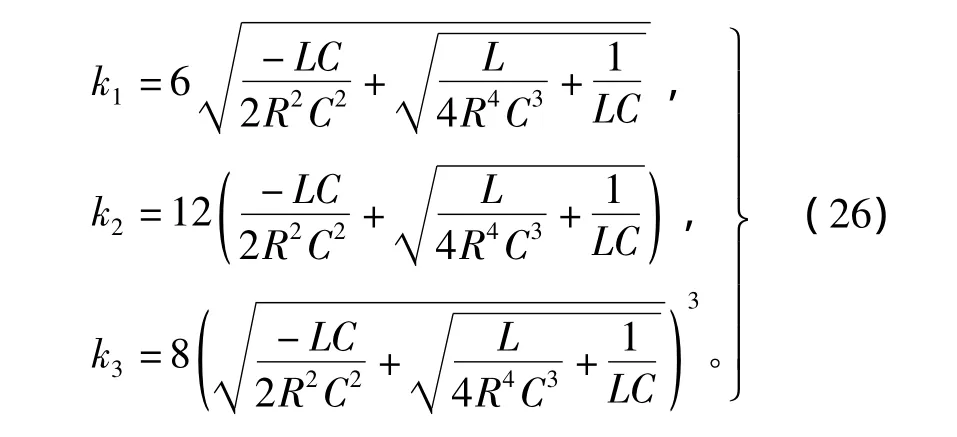
式(26)中，由于电感和电容会随着负载的变化以及干扰的变化而变化，所以会导致抗扰控制器中的参数k1、k2和k3变化。如果通过设计阻抗观测器来对电感值和电容值进行估算和校正，则抗扰控制器就会取得良好的控制效果。

3 阻抗观测器的设计

在逆变器系统中，式(3)中的电感值和电容值常为固定的设计值。在实际的系统中，由于逆变器输出谐波的存在、电感值和电容值和设计值存在偏差，温度对阻抗参数的影响、检测电路的时延、采样误差、PWM波形生成的误差、以及非线性负载的存在等，都会造成输出电压变化而形成一定的电压差。如果把这些电压差都等效为是由阻抗变化引起的，则就可以通过电压差来估算出回路阻抗。基于此，本文构造了阻抗观测器，估算实际的电感值和电容值，来修改ESO中的参数。

本系统的阻抗观测器就是估算基频的感抗值ZL和容抗值ZC，从而求出式(25)和式(26)中的L和C的值。设ω为基波角频率，T=2π/ω。根据傅里叶变换原理，对逆变器输出的任何周期波形，都可分解为基波分量是正弦和余弦的函数波形。因此，将逆变器输出电压与给定电压的差值ΔV和输出电流i展成傅氏级数后，并取相互垂直的DQ坐标系为参考，则其基波分量的幅值为

根据式(27)和式(28)，可得到电感的等效功率为

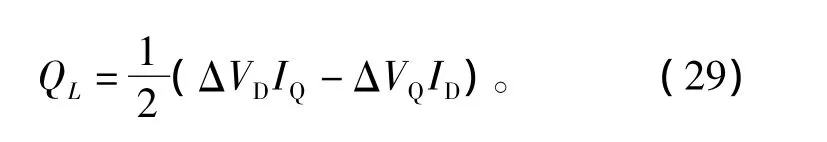
由式(29)可推出基频情况下的电感值为

同理，将逆变器输出电压V和电容电流iC展成傅氏级数后，则其基波分量的幅值为

根据式(31)和式(32)，可得到等效的电容值为

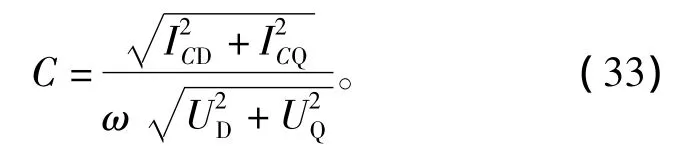
式(30)和式(33)所求出的电感值和电容值是基频情况下的参数，不受谐波影响。对于逆变器系统而言，当在某一环境下不变时，其固有特性也就确定了，所以阻抗数值相对稳定，只要在系统运行前估算出电感值和电容值即可。这就大大减小了系统运行时的实时计算量。

4 仿真和实验结果及分析

4.1 仿真结果及分析

本文在Matlab环境下，应用SIMULINK建立了系统的仿真模型。仿真时，逆变器输出滤波电容为C=40 μF，滤波电感为L=5 mH。系统给定电压为有效值220 V交流正弦波，其函数为

1)当单相逆变器独立运行时，逆变器的直流侧电压控制到500 V电压。通过对逆变器控制，使系统输出相电压有效值为220 V的交流电压。图3为稳定运行时逆变器电压电流波形。从图3可以看出，系统得到了良好的电压波形和电流波形，并且输出电流的有效值为44 A。由此可以得出，单相逆变系统在稳定运行过程中达到了预期的效果。

图3 稳定运行时逆变器电压电流波形Fig.3 Voltage and current of inverter in steady operation

2)当单相逆变器独立稳定运行时，直流侧加入干扰。图4为突加干扰时直流侧电压波形。从图4中可以看出，在t=0.02 s时，往直流侧加入谐波，则直流电压出现大幅波动。由于风力发电和太阳能发电时，逆变器直流侧电压会出现波动。本文仿真时在直流侧电压中加入3次谐波和5次谐波来使直流电压波动。图5为突加干扰时逆变器电压电流波形。从图5中可以看出，虽然输出电压和电流在t=0.02 s时出现了波动，但在一个周期内干扰消除了，即在t=0.04 s后达到稳定状态。可以看出系统具有很好的动态跟踪调节特性与很强的抗干扰特性。

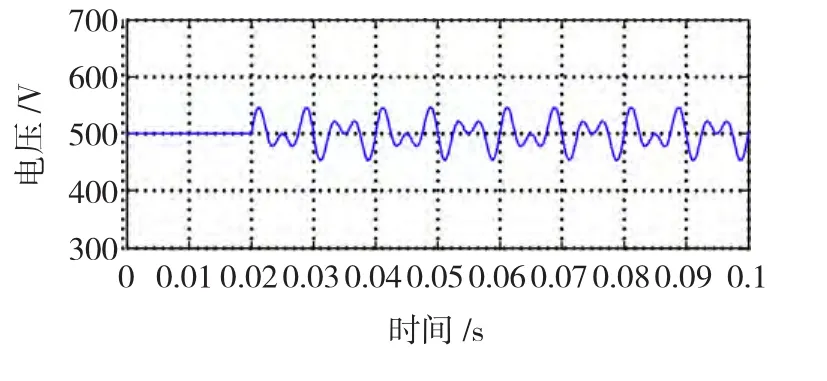
图4 突加干扰时直流侧电压波形Fig.4 Voltage of DC side when interference was added suddenly

图5 突加干扰时逆变器电压电流波形Fig.5 Voltage and current of inverter when interference was added suddenly

3)当单相逆变器独立稳定运行时，负载侧接5 Ω电阻，此时单相逆变系统的输出电压有效值为220 V，负载侧输出电流的有效值为44 A。图6为突减负载电阻时逆变器电压电流波形。从图6可以看出，当t=0.02 s时，突然减小负载，使得负载电阻由原来的5 Ω电阻切换到10 Ω电阻，在负载变化的瞬间，输出的电压波形产生畸变，但在不到一个周期内系统重新达到稳定，并且再次达到了以前输出电压的有效值220 V。此时负载侧电流的有效值为22 A。

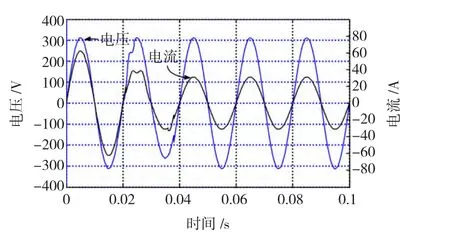
图6 突减负载电阻时逆变器电压电流波形Fig.6 Voltage and current of inverter when load was decreased suddenly

4)当单相逆变器独立稳定运行时，单相逆变系统的负载侧接入非线性负载，即接入电力二极管。图7为负载为电力二极管时逆变器电压电流波形，从图7可以看出，单相逆变器输出电压和电流波正弦，系统仍能良好稳定的运行。

图7 负载为电力二极管时逆变器电压电流波形Fig.7 Voltage and current of inverter in power diode load

4.2 实验结果及分析

为了验证本文提出的控制策略正确性，构建了单相逆变器实验系统平台。在控制系统硬件电路中，TI公司的DSP TMS320F2812A作为主控芯片，完成抗扰控制器和阻抗观测器的实现。Xilinx公司的FPGA芯片XC3S250E－TQG144用于PWM脉冲波形生成。系统工作时，通过DSP采样逆变器输出的电压和电流后，进行阻抗参数估算。在系统启动前修改抗扰控制器的控制参数。实验时，调制比为m=0.98，滤波电容为C=40 μF，滤波电感为L=5 mH，直流侧电压为500 V。

1)逆变器稳定运行时，负载为纯电阻。图8为稳定运行时逆变器电压和电流波形。从图8中可以看出，逆变器输出波形为标准正弦波形，电压波形具有很好的正弦度。图9为稳定运行时逆变器电压谐波畸变率，THD=2.9%，完全满足IEEE519－1992的要求。

图8 稳定运行时逆变器电压和电流波形Fig.8 Voltage and current of inverter in steady operation

图9 稳定运行时逆变器电压谐波畸变率Fig.9 Voltage THD of inverter in steady operation

2)直流侧电压波动。图10为带干扰时直流侧电压波形，图11为直流侧干扰时逆变器电压波形。从图10和图11中可以看出，尽管直流侧电压的波动较大，而逆变器输出的波形基本没受影响。图12为直流侧干扰时逆变器电压谐波畸变率，THD=3.6%，比没有干扰时略有增大，但也满足IEEE519－1992的要求。

图10 带干扰时直流侧电压波形Fig.10 Voltage of DC link with interference

图11 直流侧干扰时逆变器电压波形Fig.11 Voltage of inverter with DC link interference

图12 直流侧干扰时逆变器电压谐波畸变率Fig.12 Voltage THD of inverter with DC link interference

3)逆变器突加负载。图13为突增负载时逆变器电压波形。从图13中可以看出，运行初期，逆变器输出开路，不接负载。当t=0.05 s时，在逆变器输出侧突加R=17.4 Ω的负载电阻，负载电流i立即增大。在突加负载过程中和加载后，逆变器输出电压波形略有变化，但经过一个电压周期调节后恢复正常。

4)逆变器带非线性负载。图14为带非线性负载时逆变器电压波形。从图14可以看出，在负载侧串联电力二极管后，负载电流i波形为正弦半波电流，而逆变器输出电压波形仍然为正弦波，与带纯电阻负载时基本相同。

图14 带非线性负载时逆变器电压波形Fig.14 Voltage of inverter with nonlinear load

5 结语

本文将抗扰控制器应用到单相逆变器中，对控制系统进行了设计与实现。经过阻抗观测器估算ESO参数和控制器参数，解决了逆变器运行过程中的扰动问题，取得了良好的控制效果。通过逆变器在带纯电阻负载、非线性负载、直流侧电压波动和负载突变情况下时分别进行了仿真和实验，结果表明:抗扰控制器逼近能力强，逆变器输出电压波形正弦，输出电压动态品质好，谐波畸变率小，控制系统抗干扰能力强。同时，所设计的基于阻抗观测器的抗扰控制器具有良好的跟踪能力。

［1］BLAABJERG F，TEODORESCU R，LISERRE M，et al.Overview of control and grid synchronization for distributed power generation systems［J］.IEEE Transactions on Industrial Electronics，2006，53(5):1398－1409.

［2］侯世英，黄哲，肖旭，等.改进型Z源并网逆变器［J］.电机与控制学报，2012，16(12):47－53.

HOU Shiying，HUANG Zhe，XIAO Xu，et al.The improved Z source grid-connected inverter［J］.Electric Machines and Control，2012，16(12):47－53.

［3］YANG B，LI W，ZHAO Y，et al.Design and analysis of a gridconnected photovoltaic power system［J］.IEEE Transactions on Power Electronics，2010，25(4):992－1000.

［4］王继东，朱雪玲，苏海滨，等.三相光伏并网Z－源逆变器的比例谐振控制［J］.电机与控制学报，2010，14(4):86－91.

WANG Jidong，ZHU Xueling，SU Haibin，et al.Proportional-resonant control for Z-source inverter in three-phase PV grid-connected system［J］.Electric Machines and Control，2010，14(4):86－91.

［5］BPKPO R I，LIMONGI L R，ROIU D，et al.Enhanced power quality control strategy for single-phase inverters in distributed generation systems［J］.IEEE Transactions on Power Electronics，2011，26(3):798－806.

［6］姚志垒，王赞，肖岚，等.一种新的逆变器并网控制策略的研究［J］.中国电机工程学报，2006，26(18):61－64.

YAO Zhilei，WANG Zan，XIAO Lan，et al.Research on a novel grid-connected control strategy of inverter［J］.Proceedings of the CSEE，2006，26(18):61－64.

［7］蔡昆，李耀华，胜晓松，等.高性能单相电压源逆变器的输出控制［J］.电工技术学报，2005，20(1):104－107.

CAI Kun，LI Yaohua，SHENG Xiaosong，et al.Output control of the high performance single-phase voltage-source enters［J］.Transactions of China Electro Technical Society，2005，20(1):104－107.

［8］闫士杰，纪茂新，黄丽萍，等.带多频段采样观测器的单相逆

变器控制［J］.中国电机工程学报，2013，33(12):81－89.

YAN Shijie，JI Maoxin，HUANG Liping，et al.A single-phase inverter control with multi－band sampling observers［J］.Proceedings of the CSEE，2013，33(12):81－89.

［9］陈宏志，刘秀翀，钱晓龙，等.一种高性能单相正弦逆变电源的多环控制策略［J］.东北大学学报:自然科学版，2007:28(12):1685－1688.

CHEN Hongzhi，LIU Xiuchong，QIAN Xiaolong，et al.A multiloop feedback control strategy for high-performance single-phase power supply through sinusoidal inverter［J］.Journal of Northeastern University:Natural Science，2007:28(12):1685－1688.

［10］王赞，肖岚，姚志垒，等.并网独立双模式控制高性能逆变器设计与实现［J］.中国电机工程学报，2007，27(1):54－59.

WANG Zan，XIAO Lan，YAO Zhilei，et al.Design and implementation of a high performance utility-interactive inverter［J］.Proceedings of the CSEE，2007，27(1):54－59.

［11］韩京清.自抗扰控制器及其应用［J］.控制与决策，1998，13(1):19－23.

HAN Jingqing.Active disturbance rejection controller and its applications［J］.Control and Decision，1998.13(1):19－23.

［12］黄一，薛文超，赵春哲.自抗扰控制纵横谈［J］.系统科学与数学，2011，31(9):1111－1129.

HANG Yi，XUE Wenchao，ZHAO Chunzhe.Active disturbance rejection control:methodology and theoretical analysis［J］.Journal of Systems Science and Complexity，2011，31(9):1111－1129.

［13］刘翔，李东海，姜学智，等.自抗扰控制器在高阶系统中应用的仿真［J］.清华大学学报:自然科学版，2001，41(6):95－99.

LIU Xiang，LI Donghai，JIANG Xue zhi，et al.Simulation study of auto-disturbance rejection controller for high-order systems［J］.Journal of Tsinghua University:Science and Technology，2001，41(6):95－99.

［14］王建辉，顾树生.自动控制原理［M］.北京:清华大学出版社，2007.